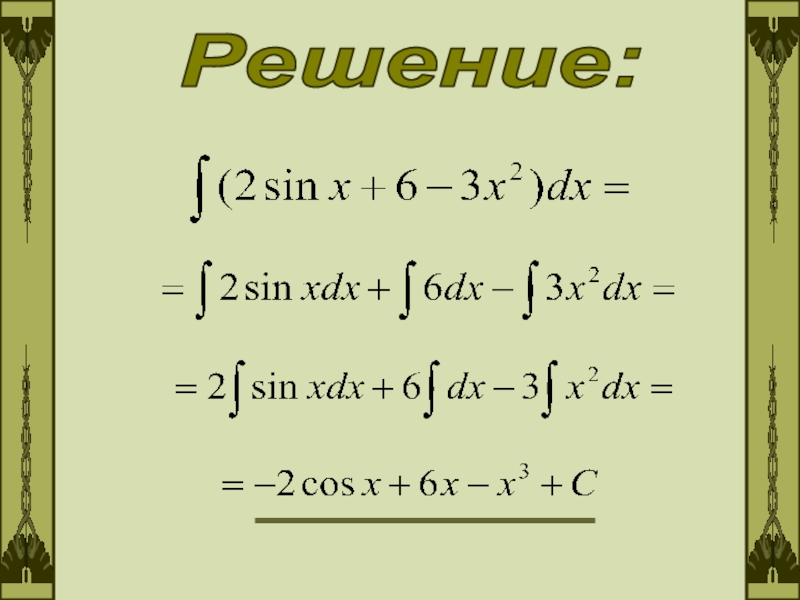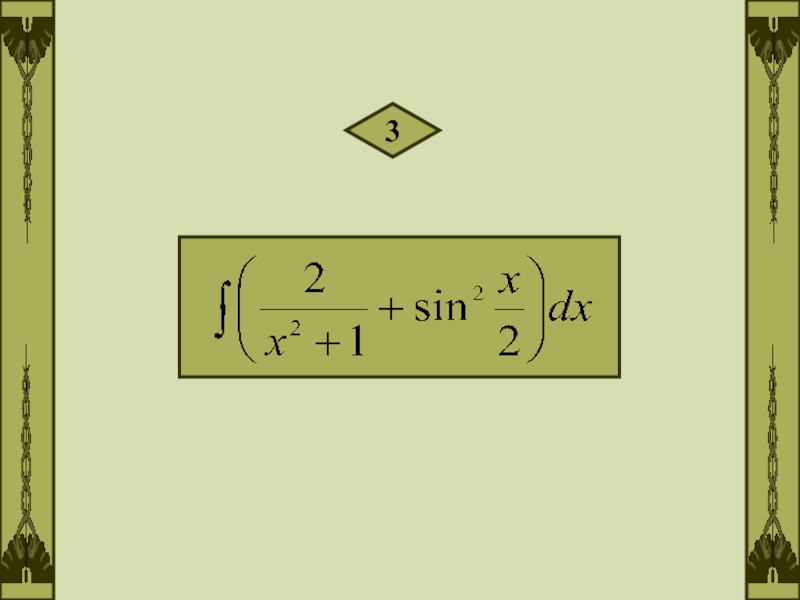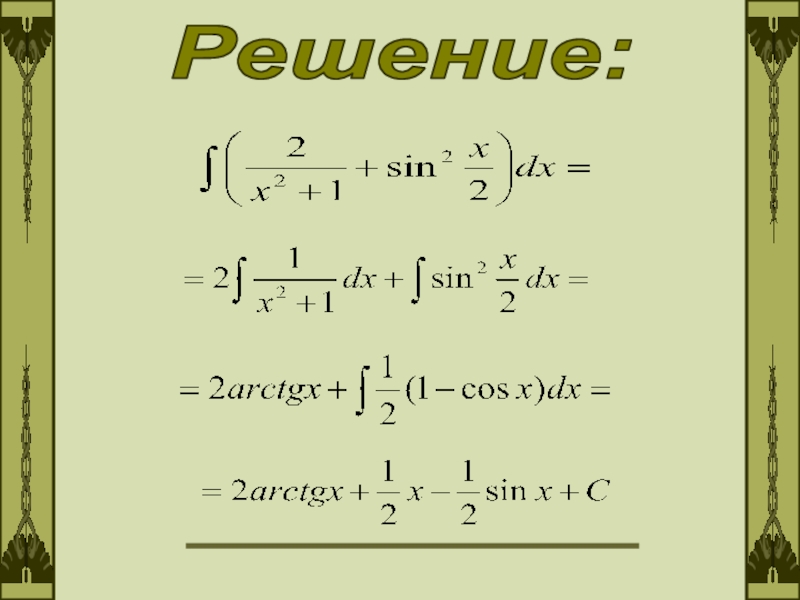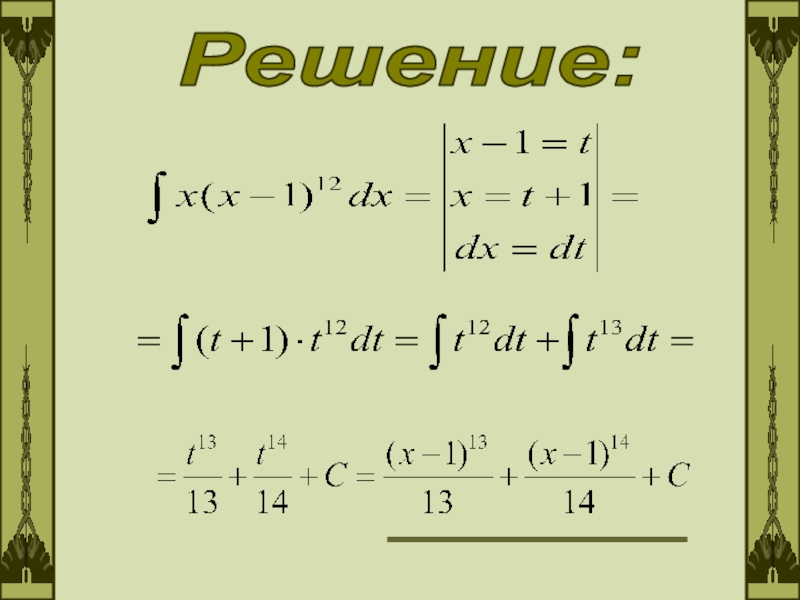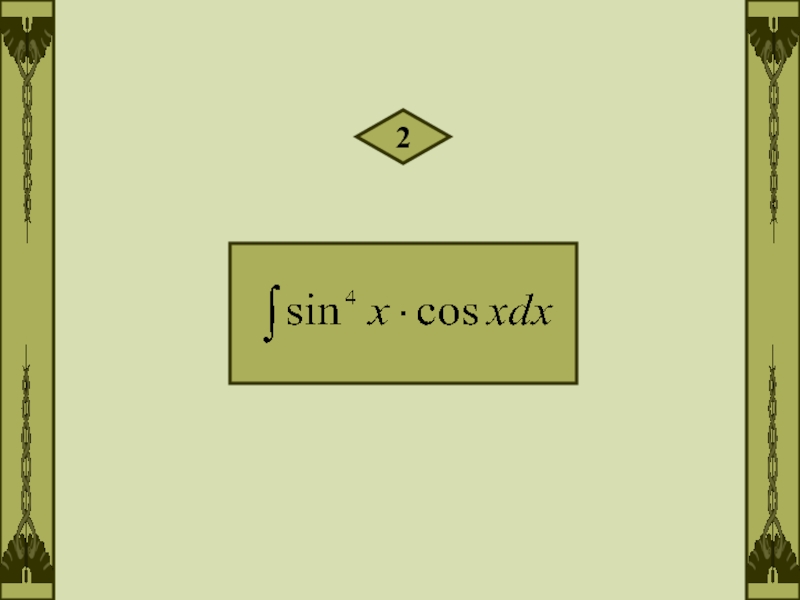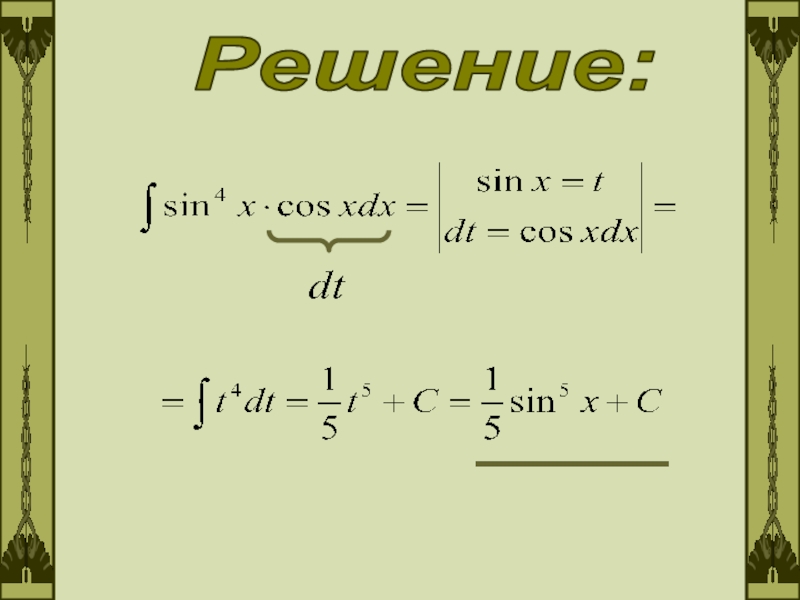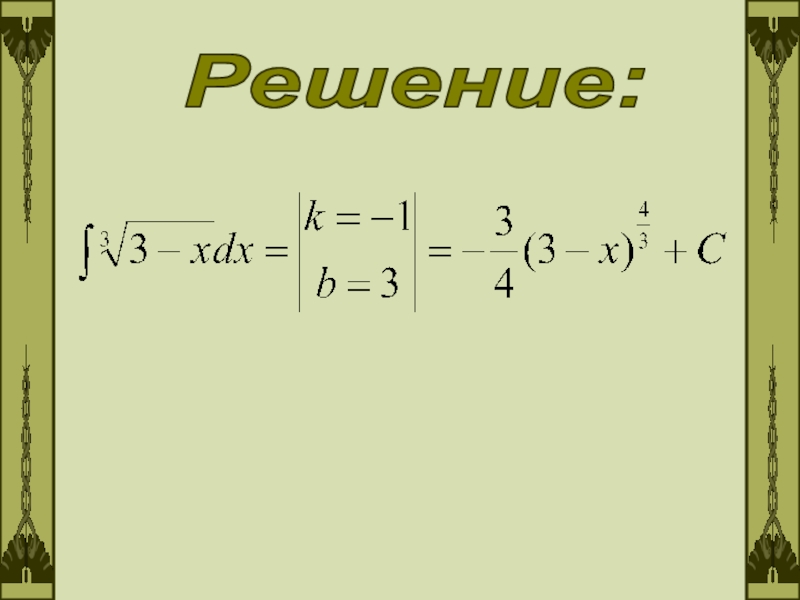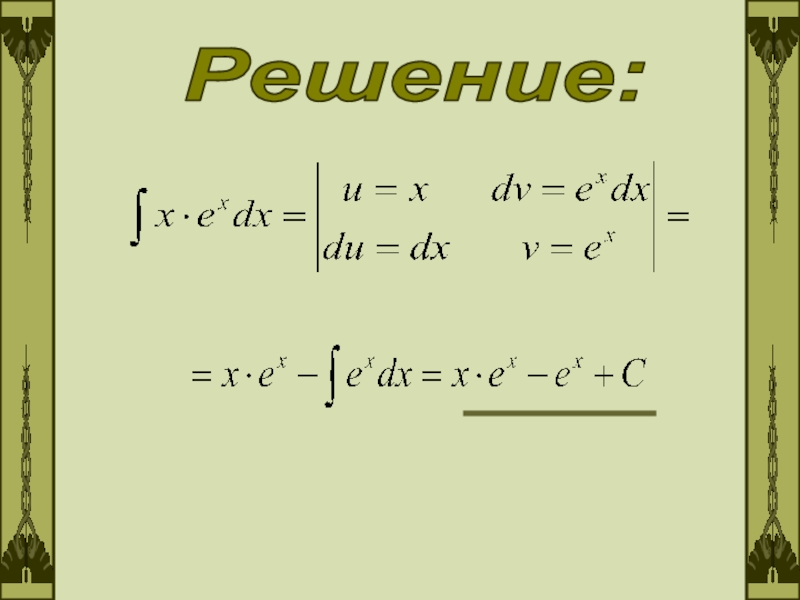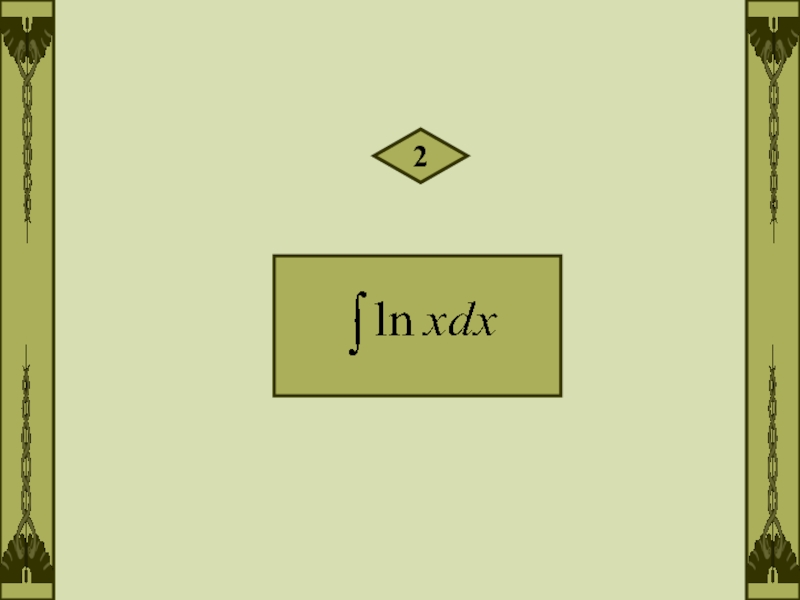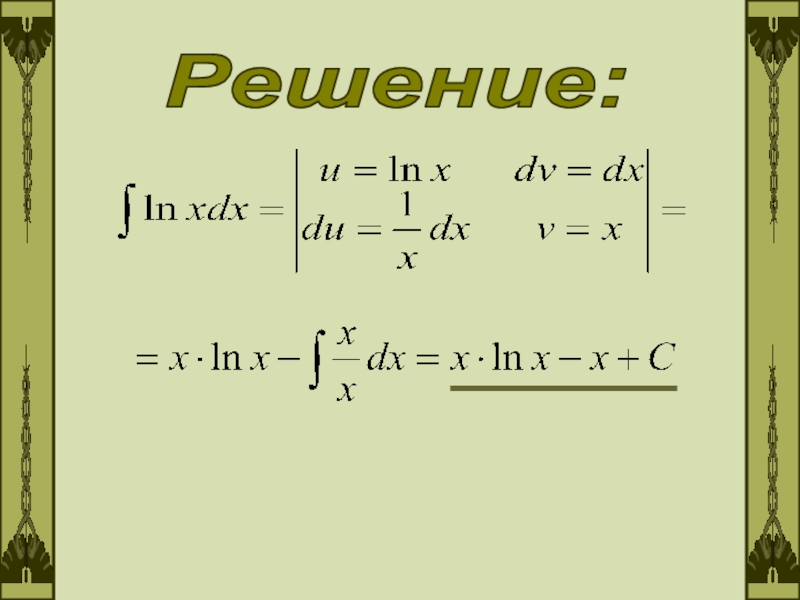Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
4. ОСНОВНЫЕ МЕТОДЫ ИНТЕГИРОВАНИЯ 1. Непосредственное интегрирование Вычисление
Содержание
- 1. 4. ОСНОВНЫЕ МЕТОДЫ ИНТЕГИРОВАНИЯ 1. Непосредственное интегрирование Вычисление
- 2. Примеры.Вычислить интегралы:1
- 3. Решение:
- 4. 2
- 5. Решение:
- 6. 3
- 7. Решение:
- 8. 2. Метод замены переменнойили метод подстановкиМетод замены переменной описывается формулой:1
- 9. Где х=φ(t) – функция, дифференцируемая на рассматриваемом
- 10. Получили одинаковый результат, следовательно по следствию из
- 11. Полученная формула показывает, что переходя к новой
- 12. Примеры.Вычислить интегралы:1
- 13. Решение:
- 14. 2
- 15. Решение:
- 16. Теорема.Пусть F(x) – некоторая первообразная для функции f(x). Тогда
- 17. Примеры.Вычислить интегралы:1
- 18. Решение:
- 19. 2
- 20. Решение:
- 21. 3. Интегрированиепо частямПусть функции u(x) и v(x)
- 22. тоже имеет первообразную наэтом промежутке и справедлива формулаТогда функция
- 23. формула интегрированияпо частям
- 24. Доказательство:Найдем производную произведения данных функций:Отсюда выражаем второе слагаемое в правой части выражения:
- 25. Слагаемые в правой части имеют первообразную на
- 26. ПосколькуТо последнее равенство часто записывают в виде:формула интегрированияпо частям
- 27. Примеры.Вычислить интегралы:1
- 28. Решение:
- 29. 2
- 30. Решение:
- 31. 3
- 32. Решение:
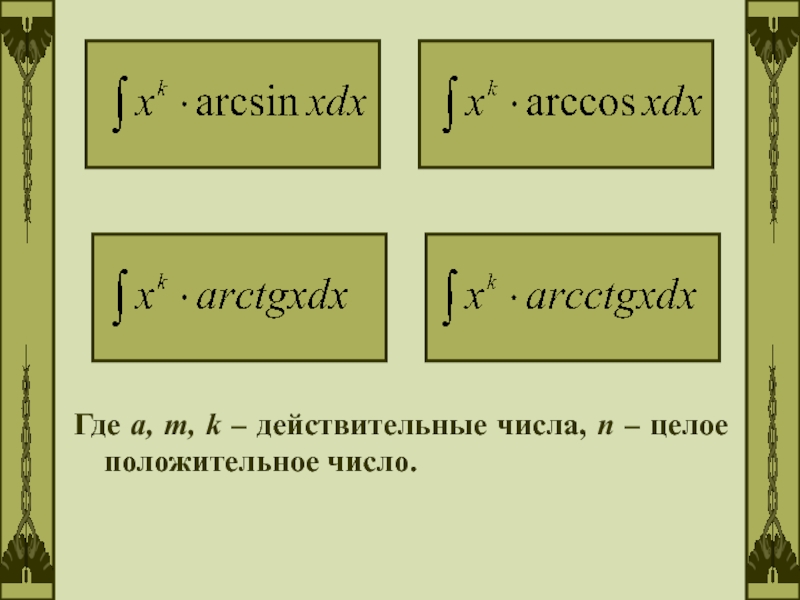
- 33. Можно показать, что формула интегрирования по частям применима для следующих типов интегралов:
- 34. Где a, m, k – действительные числа, n – целое положительное число.
- 35. Скачать презентанцию
Примеры.Вычислить интегралы:1
Слайды и текст этой презентации
Слайд 14. ОСНОВНЫЕ МЕТОДЫ
ИНТЕГИРОВАНИЯ
1. Непосредственное
интегрирование
Вычисление интегралов с помощью основных
свойств неопределенного интеграла и таблицы интегралов называется непосредственным интегрированием.
Слайд 82. Метод замены переменной
или метод подстановки
Метод замены переменной описывается формулой:
1
Слайд 9Где х=φ(t) – функция, дифференцируемая на рассматриваемом промежутке.
Покажем справедливость этой
формулы.
Найдем производную по t от левой и правой части
выражения (1):Слайд 10Получили одинаковый результат, следовательно по следствию из теоремы Лагранжа левая
и правая части выражения (1) отличаются на некоторую постоянную.
Т.к. сами
неопределенные интегралы определены с точностью до произвольного постоянного слагаемого, то эту постоянную можно опустить.Т.об,