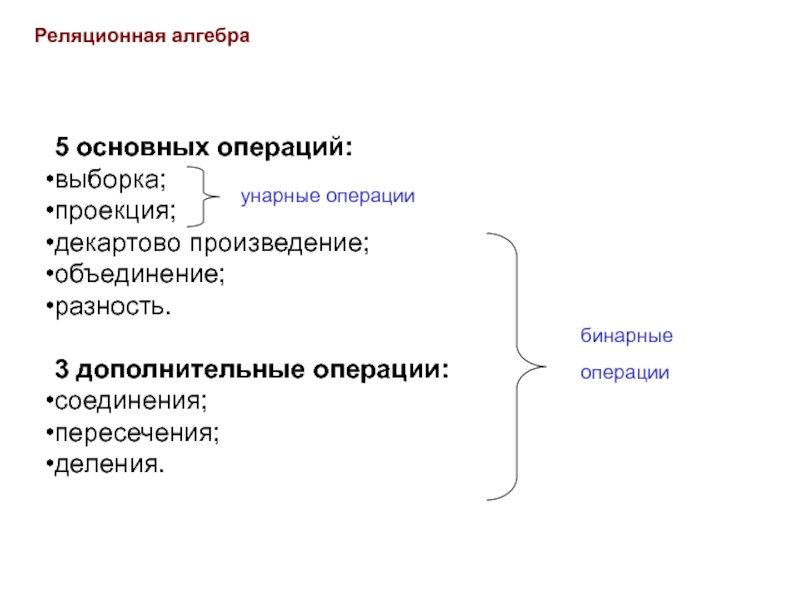
результатом новое отношение, которое содержит только те кортежи из отношения
R, которые удовлетворяют заданному условию (предикату). Предикаты могут соединяться с помощью логических операций «AND», «OR» и «NOT», образуя составные предикаты.ДАНО:
R — отношение, определенное на атрибутах А=(а1, а2, … аn).
σ предикат (R)
(R)
Пример: Составьте список всех студентов группы МФЭУ2-09-01
σ группа = мфэу2-09-01 (Студент)