Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение СЛАУ методом Гаусса. Алгебра матриц
Содержание
- 1. Решение СЛАУ методом Гаусса. Алгебра матриц
- 2. Рассмотрим СЛАУ n-го порядка: Запишем ее
- 3. Алгоритм метода. 0) Выберем строку, содержащую 1-й
- 4. 2) Поступая аналогично, выбираем 2-ю ведущую строку
- 5. Обратный ход метода ГауссаРаскроем последнюю строку треугольной
- 6. Пример 1. Решить СЛАУРешение.
- 7. Пример2. Решить СЛАУ методом ГауссаПроверкаОтвет:
- 8. 2. Алгебра матрицОпределения.Матрицей размера (m x n)
- 9. Операции над матрицами1) Сложение матриц.Определение. Суммой матриц
- 10. Операции над матрицами3) Произведение двух матриц.Определение. Пусть
- 11. Спасибо за внимание !
- 12. Скачать презентанцию
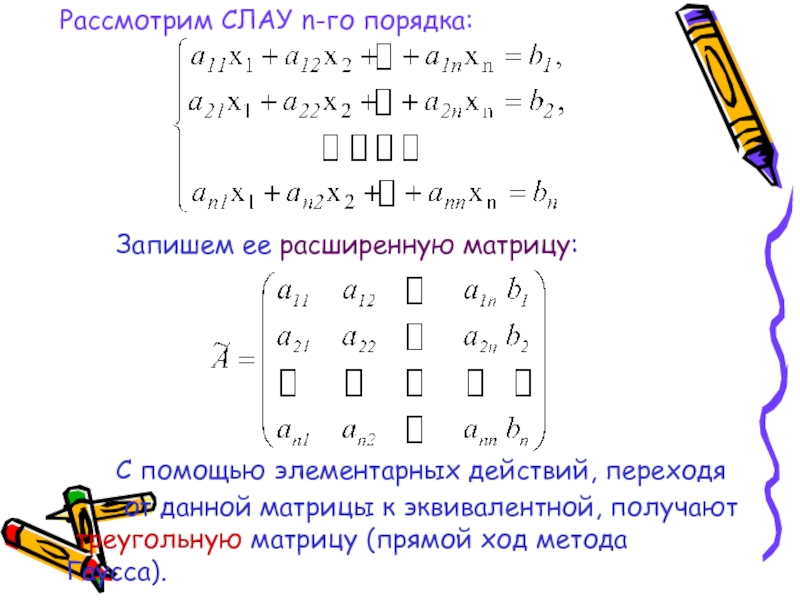
Рассмотрим СЛАУ n-го порядка: Запишем ее расширенную матрицу: С помощью элементарных действий, переходя от данной матрицы к эквивалентной, получают треугольную матрицу (прямой ход метода Гаусса).
Слайды и текст этой презентации
Слайд 1Решение СЛАУ методом Гаусса.
Алгебра матриц.
1.Метод последовательных исключений
(метод Гаусса)
Слайд 2 Рассмотрим СЛАУ n-го порядка:
Запишем ее расширенную матрицу:
С помощью элементарных действий, переходя
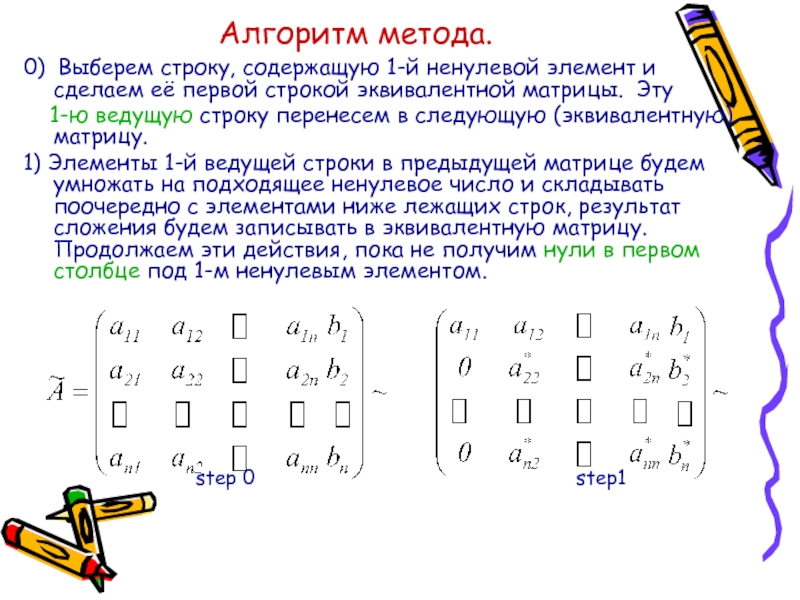
к эквивалентной, получают треугольную матрицу (прямой ход метода Гаусса).Слайд 3Алгоритм метода.
0) Выберем строку, содержащую 1-й ненулевой элемент и
сделаем её первой строкой эквивалентной матрицы.
Эту1-ю ведущую строку перенесем в следующую (эквивалентную) матрицу.
1) Элементы 1-й ведущей строки в предыдущей матрице будем умножать на подходящее ненулевое число и складывать поочередно с элементами ниже лежащих строк, результат сложения будем записывать в эквивалентную матрицу. Продолжаем эти действия, пока не получим нули в первом столбце под 1-м ненулевым элементом.
step 0 step1
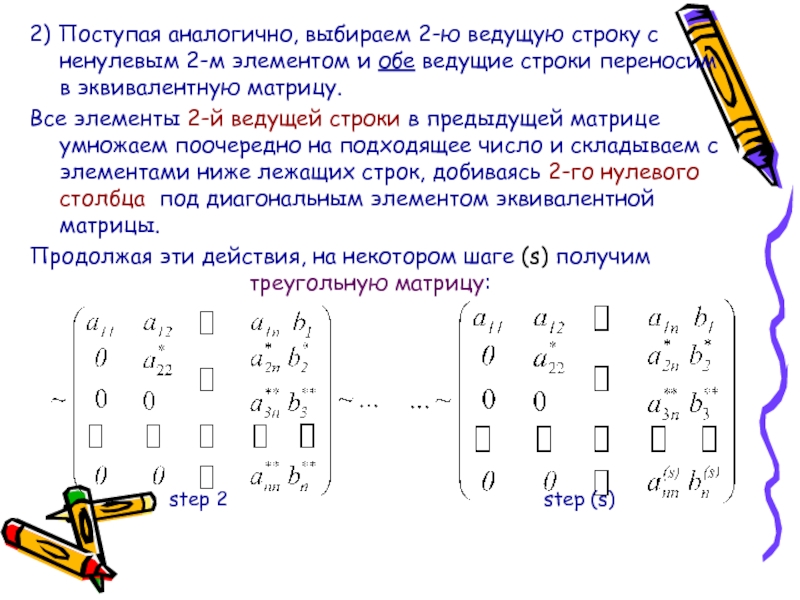
Слайд 42) Поступая аналогично, выбираем 2-ю ведущую строку с ненулевым 2-м
элементом и обе ведущие строки переносим в эквивалентную матрицу.
Все
элементы 2-й ведущей строки в предыдущей матрице умножаем поочередно на подходящее число и складываем с элементами ниже лежащих строк, добиваясь 2-го нулевого столбца под диагональным элементом эквивалентной матрицы.Продолжая эти действия, на некотором шаге (s) получим треугольную матрицу:
step 2 step (s)
Слайд 5Обратный ход метода Гаусса
Раскроем последнюю строку треугольной матрицы.
Она означает уравнение:
При находим
Поднимаясь на строку вверх, раскроем (n-1)-е уравнение, оно
содержит неизвестные xn-1 и xn,
последнее уже найдено, подставим его и найдем xn-1.
Поступая аналогично, поднимаемся снизу вверх по строчкам треугольной матрицы, последовательно находя xn-2, xn-3,…,x1. Решение (x1, x2,…,xn) получено.
Слайд 82. Алгебра матриц
Определения.
Матрицей размера (m x n) называется таблица чисел,
имеющая m строк и n столбцов.
Матрица AT называется транспонированной относительно
матрицы А, если столбцы одной из матриц совпадают со строками другой. (m x n) (n x m)
Слайд 9Операции над матрицами
1) Сложение матриц.
Определение. Суммой матриц A и B
одинаковой размерности называется матрица C=A+B, такой же размерности, элементы которой
равны сумме соответствующих элементов обеих матриц.2) Умножение матрицы на число.
Определение. Произведением матрицы А (m x n) на число k называется матрица B=kA, той же размерности, элементы которой равны произведениям элементов матрицы А на число k.
Слайд 10Операции над матрицами
3) Произведение двух матриц.
Определение. Пусть число столбцов матрицы
А(m x n) равно числу строк матрицы B (n x
p).Произведением матриц A и B называется матрица C (m x р), обозначаемая C=AB, элементы которой вычисляются по формуле:
(«строка на столбец»).