Слайд 1По книге: Фаддeев М.А., Чупрунов Е.В. Лекции по атомной физике
(2008, Физматлит).
В качестве показательного примера рассчитаем собственные значения и собственные
функции простейшего гамильтониана.
То есть, определим энергетический спектр простейшей квантовомеханической системы и найдем решения стационарного уравнения Шредингера
для простейших условий.
6.7. Стационарные состояния частицы в одномерной потенциальной яме
Начнем с одномерной задачи о частице «в бесконечно глубокой потенциальной яме с плоским дном».
Пусть для микрообъекта массы m зависимость потенциальной энергии от единственной координаты имеет вид:
Слайд 2Классический аналог – задача о движении частицы между вертикальными жесткими
стенками
при x=0 и x=a. Для нее
разрешены любые значения энергии частицы.
Время нахождения частицы вблизи любой точки ее траектории одинаково (модуль скорости постоянен).
В волновой механике говорят не о движении, а о состоянии микрообъекта.
Гамильтониан для заданной потенциальной функции U(х) «внутри ямы» (при 0
Одномерное стационарное уравнение Шредингера
с указанным гамильтонианом можно привести к виду:
Слайд 3Действительные решения этого уравнения можно представить в форме:
где A и
B – постоянные. Введено обозначение
В областях xa
волновая функция должна обращаться в 0, поскольку попадание частицы в эти области потребовало бы совершения над ней бесконечной работы. Из свойства непрерывности волновой функции получаем граничные условия:
Первое из этих граничных условий задает B=0, а второе приводит к соотношению:
Следовательно, величина k может принимать лишь дискретные значения
Значение n=0 отброшено, поскольку оно задает волновую функцию (x)=0 , которой соответствует нулевая вероятность найти частицу где-либо.
Слайд 4Дискретным значениям k соответствуют дискретные значения энергии:
Это и есть собственные
значения гамильтониана.
Каждому значению энергии соответствует собственная волновая функция:
Коэффициент A находится
из условия нормировки вероятности:
Итого: стационарные состояния микрообъекта в бесконечно глубокой потенциальной яме с плоским дном описываются волновыми функциями
Целое число n, нумерующее дискретные состояния «частицы», называют квантовым числом.
В рассмотренном случае энергия состояния зависит от квантового числа квадратично.
Слайд 5Полученный результат соответствует общему свойству квантовых систем – финитному «движению»
(ограниченной области локализации волновой функции) соответствует дискретный спектр стационарных состояний
и соответствующих значений энергии. В классической физике спектр разрешенных значений энергии частицы в потенциальной яме непрерывен.
Полные волновые функции стационарных состояний можно получить умножением координатной части (x) на экспоненциальные временные зависимости:
Математически они представляют собой стоячие волны, аналогичные фигурировавшим при выводе формулы Рэлея-Джинса (там они были
трехмерными). Дискретная величина kn имеет смысл волнового числа.
Рассмотрим подробнее конкретные состояния.
Начнем с состояния, которое могло бы соответствовать n=0. Его
несуществование означает, что квантовая частица в потенциальной яме не может иметь нулевую (соответствующую потенциальной энергии дна ямы) энергию. Классическая частица могла бы «покоиться на дне ямы». Для квантовой это запрещено.
Слайд 6
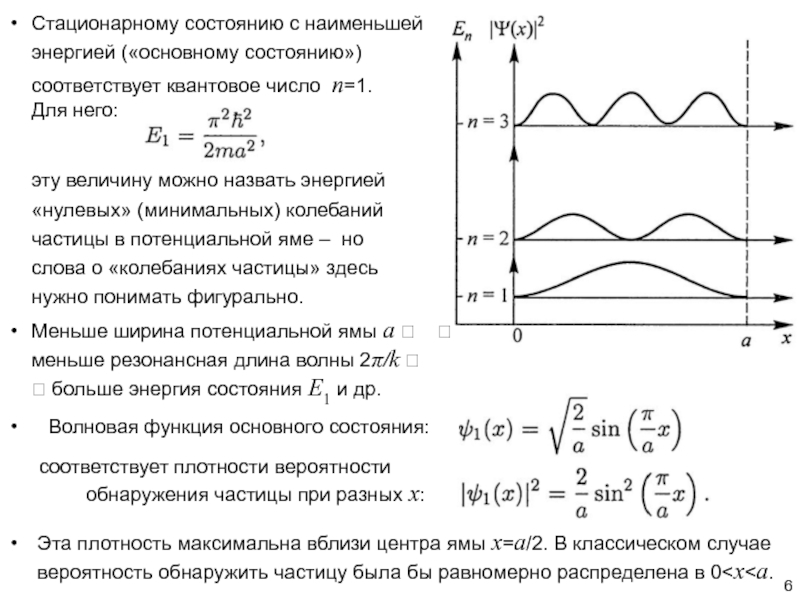
Эта плотность максимальна вблизи центра ямы х=a/2. В классическом случае
вероятность обнаружить частицу была бы равномерно распределена в 0
с наименьшей энергией («основному состоянию»)
соответствует квантовое число n=1.
Для него:
эту величину можно назвать энергией «нулевых» (минимальных) колебаний частицы в потенциальной яме – но слова о «колебаниях частицы» здесь нужно понимать фигурально.
Меньше ширина потенциальной ямы a меньше резонансная длина волны 2/k
больше энергия состояния E1 и др.
Волновая функция основного состояния:
соответствует плотности вероятности
обнаружения частицы при разных x:
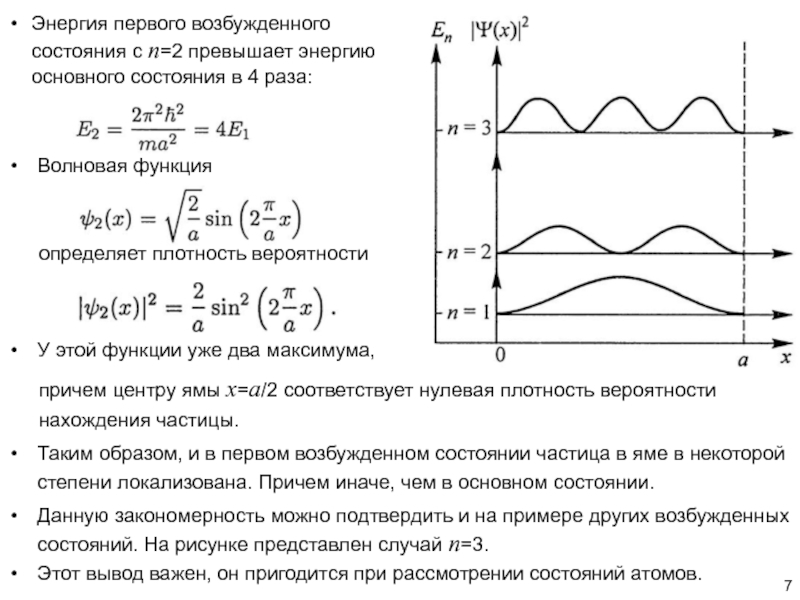
Слайд 7причем центру ямы x=a/2 соответствует нулевая плотность вероятности нахождения частицы.
Таким
образом, и в первом возбужденном состоянии частица в яме в
некоторой степени локализована. Причем иначе, чем в основном состоянии.
Данную закономерность можно подтвердить и на примере других возбужденных состояний. На рисунке представлен случай n=3.
Этот вывод важен, он пригодится при рассмотрении состояний атомов.
Энергия первого возбужденного состояния с n=2 превышает энергию основного состояния в 4 раза:
Волновая функция
определяет плотность вероятности
У этой функции уже два максимума,
Слайд 8
Выделим три пространственные области 1, 2 и 3:
xa.
Рассмотрим отдельно случаи E
E>U0 . Первому из них в классической физике соответствует финитный (ограниченный размерами потенциальной ямы), а второму – инфинитный характер движения частицы.
Следующий, несколько более сложный случай – нахождение стационарных состояний (собственных функций гамильтониана) для частицы в одномерной прямоугольной потенциальной яме конечной глубины.
Пусть зависимость потенциальной энергии от координаты имеет вид:
Обозначим путь нахождения собственных значений и собственных функций гамильтониана, определяющих спектр энергии частицы и волновые функции стационарных состояний.
Слайд 9После подстановки такого гамильтониана в уравнение Шредингера
и алгебраических преобразований получаем
для волновой функции уравнения:
где вновь
Положительный
параметр ϰ определен формулой:
Рассмотрим сначала случай EПо определению, гамильтониан выражается как:
В рассматриваемом случае:
Слайд 10Действительные решения очевидны – экспоненты для 1 и 2 областей
и гармонические функции для области 2. Для последующего анализа их
удобно записать в виде:
Присутствующие здесь коэффициенты (постоянные интегрирования) определяются из граничных условий и условий нормировки.
Коэффициенты A2 и B2 следует приравнять 0, чтобы волновая функция оставалась ограниченной в пределе x – и x + соответственно.
Для вычисления оставшихся констант нужно воспользоваться свойством непрерывности волновой функции (1, 2 и 3 – это одна и та же функция на различных участках оси x) и ее производной.
«Сшивка» должна производиться при x=0 и при x=a .
Получим систему уравнений для коэффициентов AA1, BB1 , A0 и .
Слайд 11(Слева показано условие «сшивки», справа – следующее из него уравнение.)
Деление
первого уравнения на второе и третьего на четвертое дают:
После ряда
преобразований от тангенсов можно перейти к синусам:
где введено новое обозначение
Первое из этих уравнений дает
(Постоянная изначально вводилась в уравнении
И мы, считая ее положительной, без снижения общности можем потребовать, чтобы она принадлежала интервалу [0, /2] .)
Слайд 12Второе уравнение
при переходе к обратным тригонометрическим величинам дает:
Целочисленный параметр n
появляется из-за неоднозначности решения.
Далее он играет роль квантового числа.
После подстановки
из первого уравнения получаем уравнение относительно k:
Заметим, что при E<
(Это ясно из определений k и ϰ0 :
и .)
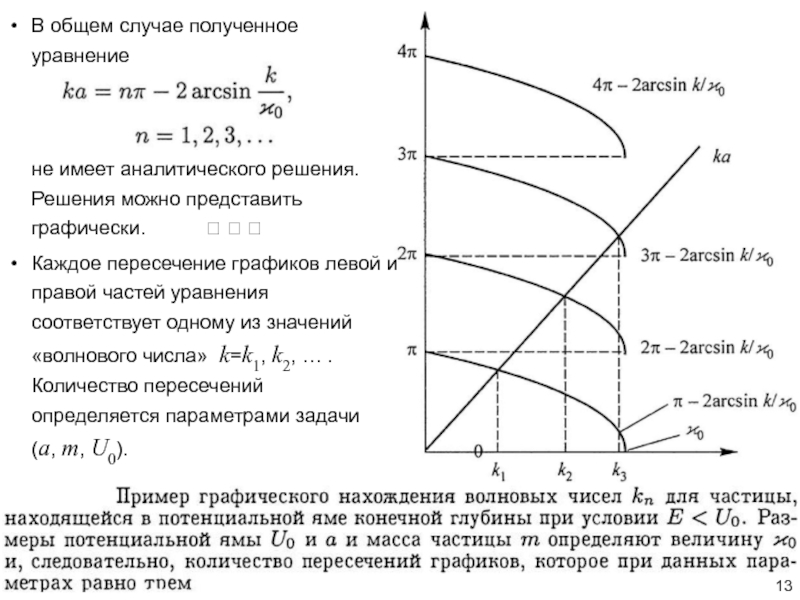
Слайд 13В общем случае полученное уравнение
не имеет аналитического решения.
Решения
можно представить графически.
Каждое пересечение графиков левой и правой частей уравнения соответствует одному из значений «волнового числа» k=k1, k2, … . Количество пересечений определяется параметрами задачи (a, m, U0).
Слайд 14Параметр
не зависит от ширины ямы a.
С уменьшением ширины ямы
уменьшается наклон прямой, а набор пересекаемых с ней фрагментов синусоиды
не изменяется.
Точки пересечения смещаются вправо – растут значения kn, а следовательно, и энергии состояний.
При этом число возможных состояний (число точек пересечения) уменьшается.
Число локализованных состояний (с E
представлен качественный вид графика плотности вероятности
для волновых функций двух первых локализованных стационарных состояний частицы в потенциальной яме конечной глубины.
Основное состояние вновь
соответствует квантовому числу n=1.
И вновь его энергия ненулевая – выше дна ямы.
Внутри потенциальной ямы (0
волновые функции синусоидальны, вне ямы экспоненциально спадают. На границе этих областей (и даже за этой
границей, где Eвероятности обнаружить частицу – ненулевая.
Слайд 16Один из главных выводов из предыдущего рассмотрения – дискретность спектра
локализованных состояний частицы, в классической физике соответствующей частице, совершающей финитное
движение в потенциальной яме.
Перейдем теперь к случаю E>U0 (при тех же остальных условиях задачи), соответствующему инфинитному движению частицы через область потенциальной ямы 2 в направлении из области 1 в область 3.
Вид гамильтониана сохранится:
Но из-за изменения знака разности
(E–U0) уравнения Шредингера
для областей теперь удобнее записать в виде:
Введены обозначения:
Слайд 17Решение запишем в комплексной форме:
С учетом временной части волновых функций,
первые члены каждой суммы представляют волну, бегущую в положительном направлении
оси координат, а вторые – волну, бегущую в отрицательном направлении.
Постоянные интегрирования A, B и C должны быть найдены из граничных условий.
Четыре уравнения, позволяющие определить постоянные интегрирования, можно получить из условий «сшивки» волновых функций и их производных на границах областей.
Для делокализованных состояний (соответствующих инфинитному движению частиц в классической модели) условие нормировки полной вероятности на 1 использовать нельзя. Нормировка должна быть определена специальным
образом – например, заданием «амплитуды падающей волны» A1.
В общем случае, нельзя использовать и условие обращения волновой функции в 0 на бесконечности. Однако, если рассматривать волну (частицу), бегущую
из – в положительном направлении оси координат, можно положить, что
отраженная волна в области 3 будет отсутствовать: B2=0.
Слайд 18Для проводимого рассмотрения существенным является следующее:
при определении уравнений и граничных
условий для случая E>U0 не накладывается никаких условий, приводящих к
дискретности значений k и k1.
Вследствие этого и спектр собственных значений гамильтониана оказывается непрерывным.
Итого, спектр собственных значений гамильтониана, совпадающий со спектром энергий стационарных состояний частицы, в присутствии потенциальной ямы конечной глубины состоит из двух частей – дискретной и непрерывной.
Дискретная часть спектра собственных значений всегда содержит хотя бы одно значение – даже для ямы сколь угодно малых (но конечных) глубины и ширины. Полное число собственных значений конечно.
Наименьшее из собственных значений соответствует энергии основного состояния частицы в яме. Она всегда больше энергии дна ямы – на величину «энергии нулевых колебаний».
Дискретным собственным значениям соответствуют локализованные состояния частицы, плотность вероятности которых в основном сосредоточена внутри ямы. Тем не менее, она не обращается в 0 и за ее пределами – кроме как на бесконечности.
Слайд 19Математически, состояниям дискретного спектра гамильтониана соответствуют волновые функции в виде
стоячих волн. Плотность вероятности обнаружения частицы в разных точках внутри
ямы распределена неравномерно и различным образом для разных состояний.
Непрерывной части спектра собственных значений гамильтониана соответствуют полностью делокализованные состояния, описываемыми волновыми функциями в виде бегущих волн.