Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
8 класс в прямоугольном треугольнике Л.С. Атанасян Геометрия 7-9 Савченко Е.М.,
Содержание
- 1. 8 класс в прямоугольном треугольнике Л.С. Атанасян Геометрия 7-9 Савченко Е.М.,
- 2. В прямоугольном треугольнике из вершины прямого угла
- 3. ОпределениеПовторениеСреднее арифметическое
- 4. BCAbacbcach
- 5. BCAD
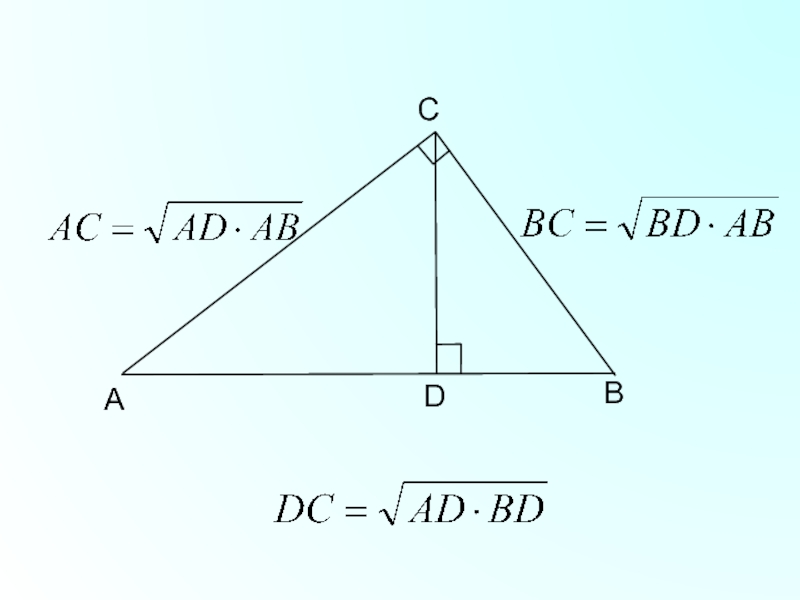
- 6. BCADКатет прямоугольного треугольника есть среднее пропорциональное для
- 7. BCAD
- 8. BCADВысота прямоугольного треугольника, проведенная из вершины прямого
- 9. BCАD
- 10. BCАDБлиц-опрос. 169201512
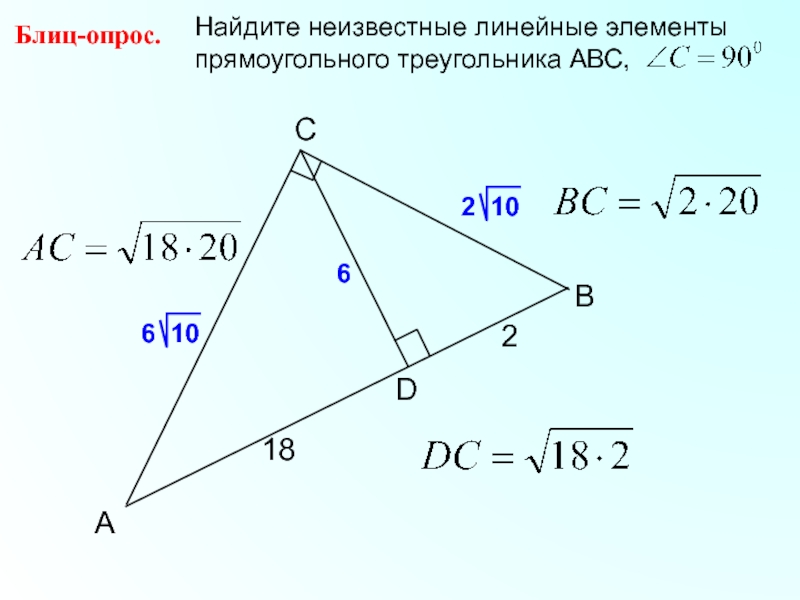
- 11. BCАDБлиц-опрос. 1826
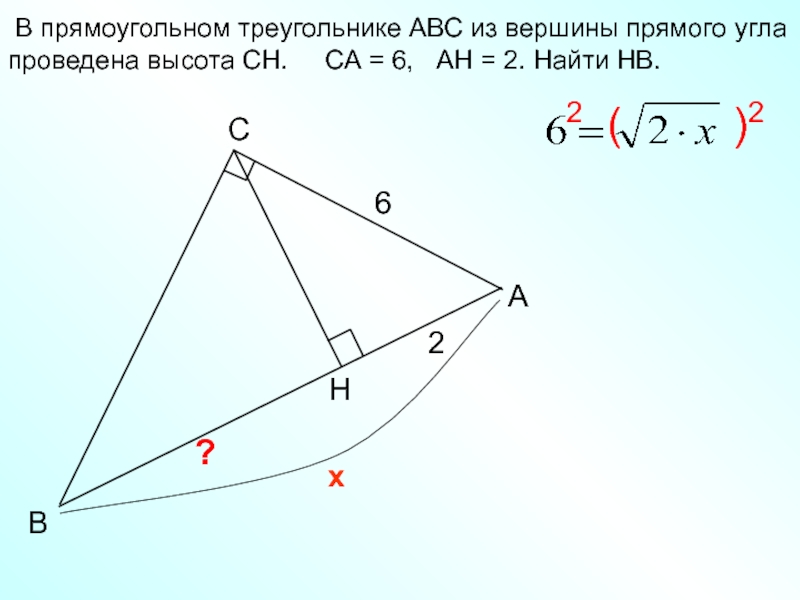
- 12. АCВН62х В прямоугольном треугольнике АВС из вершины
- 13. BCАD25В прямоугольном треугольнике АВС из вершины прямого угла проведена высота СD. По данным чертежа найти СD.ЕТ816
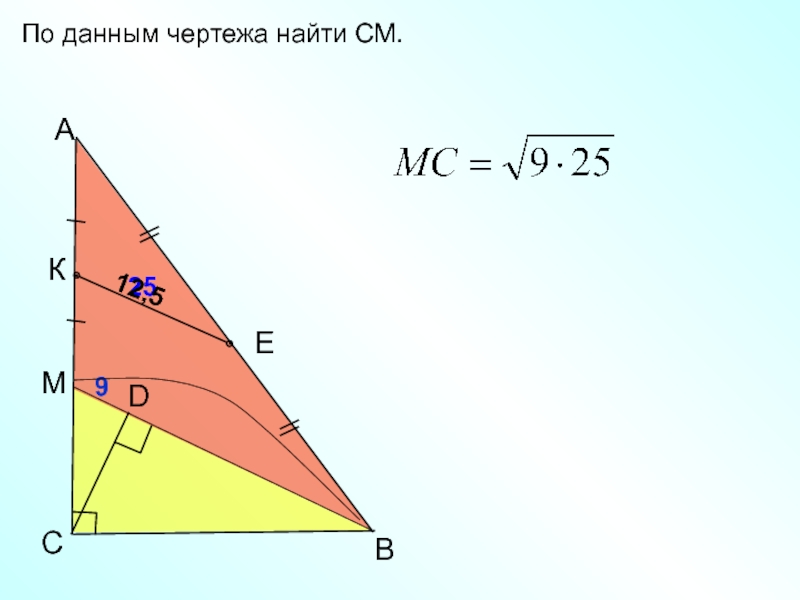
- 14. BCАDПо данным чертежа найти СМ.КЕ92512,5М
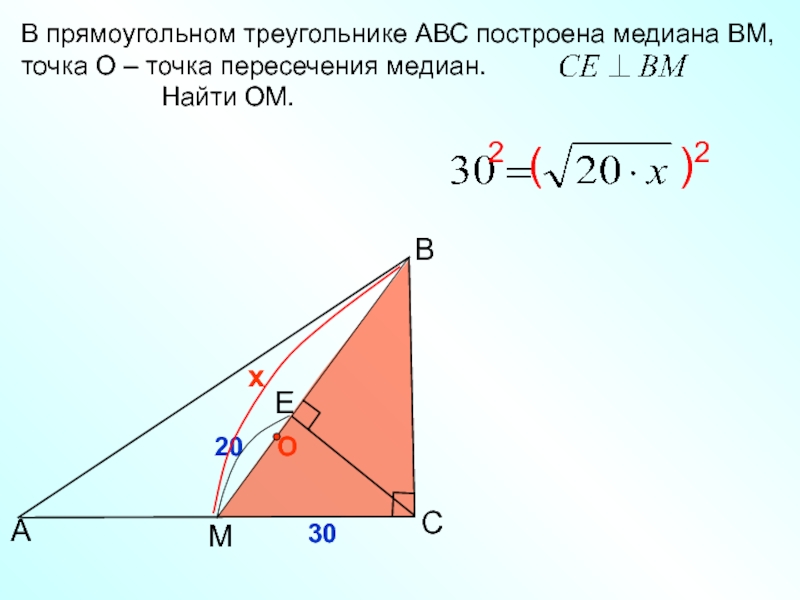
- 15. BCАВ прямоугольном треугольнике АВС построена медиана ВМ,
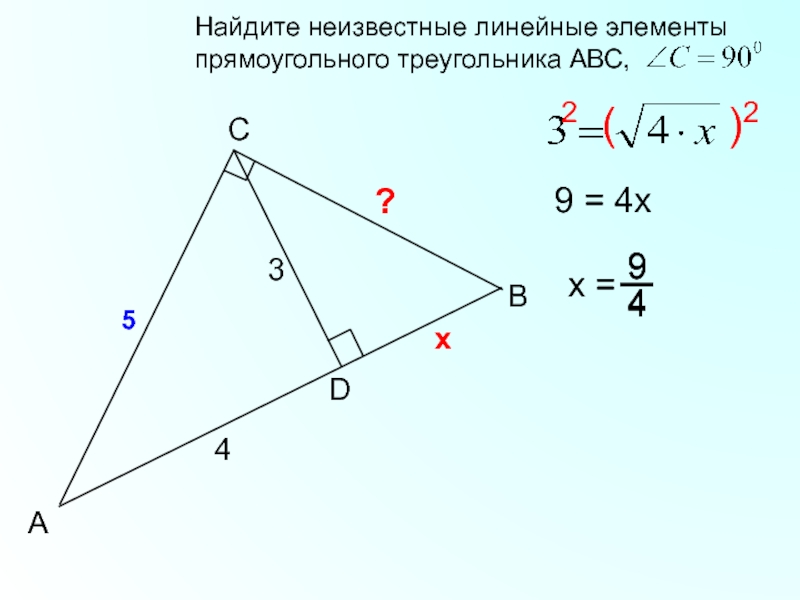
- 16. BCАD345х2 ( )29 = 4х?
- 17. ВАА1С1С1,7м3,4м№ 579
- 18. Длина
- 19. D Для
- 20. Для
- 21. На
- 22. Два
- 23. Скачать презентанцию
Слайды и текст этой презентации
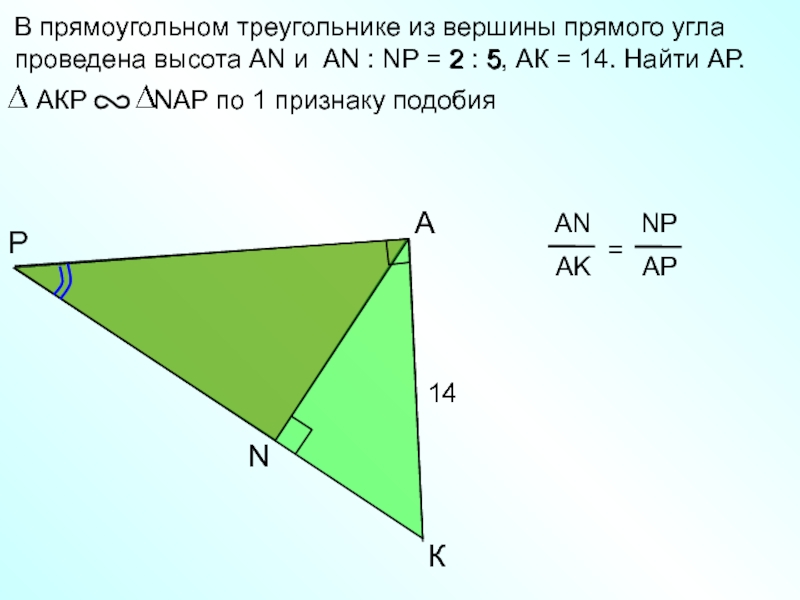
Слайд 2В прямоугольном треугольнике из вершины прямого угла проведена высота АN
и АN : NP = 2 : 5, АК =
14. Найти АР.P
К
A
N
AK
NP
14
2
5
14
Слайд 3Определение
Повторение
Среднее арифметическое
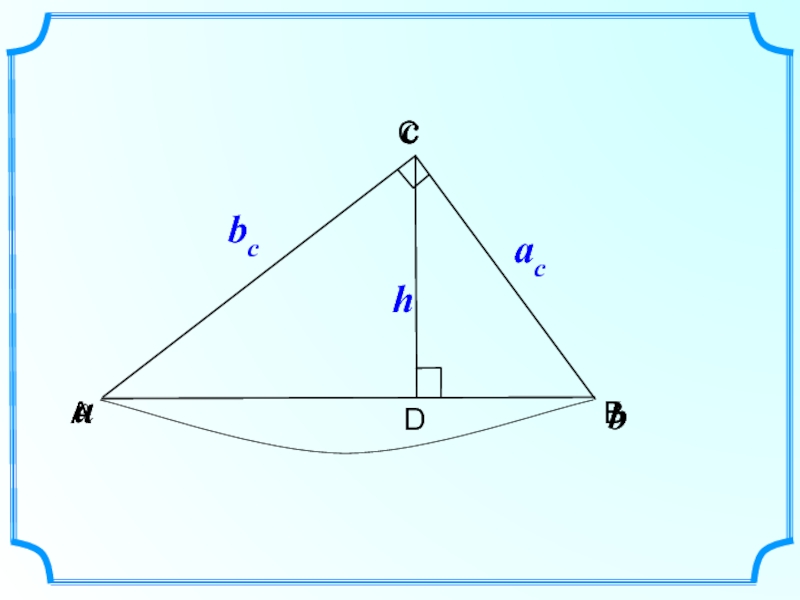
Отрезок XY называется
средним геометрическим (или средним пропорциональным) для отрезков, на которые делится гипотенуза этой высотой.Слайд 6B
C
A
D
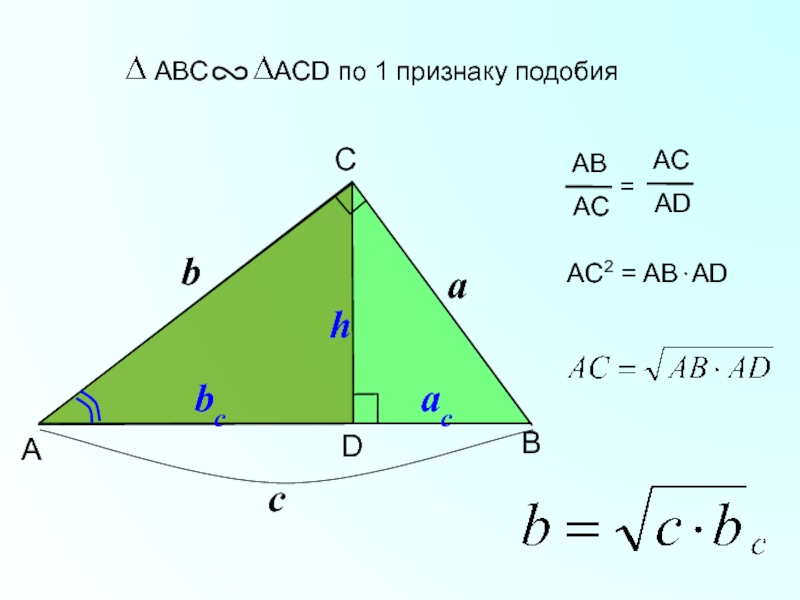
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка
гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого
угла.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекции катета на гипотенузу.
Слайд 8B
C
A
D
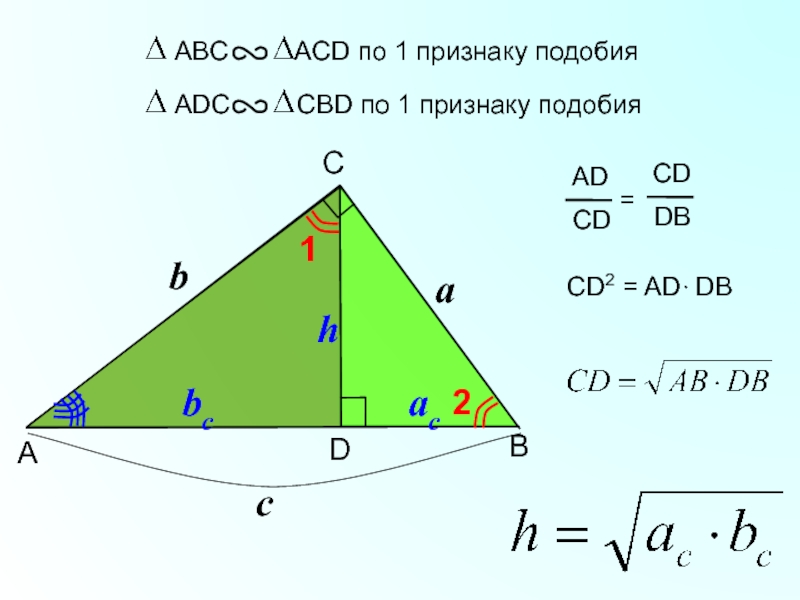
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее
пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Высота прямоугольного
треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для проекций катетов на гипотенузу.Слайд 12А
C
В
Н
6
2
х
В прямоугольном треугольнике АВС из вершины прямого угла проведена
высота СН. СА = 6, АН =
2. Найти НВ.2 ( )2
?
Слайд 13B
C
А
D
25
В прямоугольном треугольнике АВС из вершины прямого угла проведена высота
СD. По данным чертежа найти СD.
Е
Т
8
16
Слайд 15B
C
А
В прямоугольном треугольнике АВС построена медиана ВМ, точка О –
точка пересечения медиан.
Найти ОМ.М
Е
20
О
30
2 ( )2
Слайд 17В
А
А1
С1
С
1,7м
3,4м
№ 579
Для
определения высоты столба А1С1 использовали шест с вращающейся планкой.
Чему
равна высота столба? ?
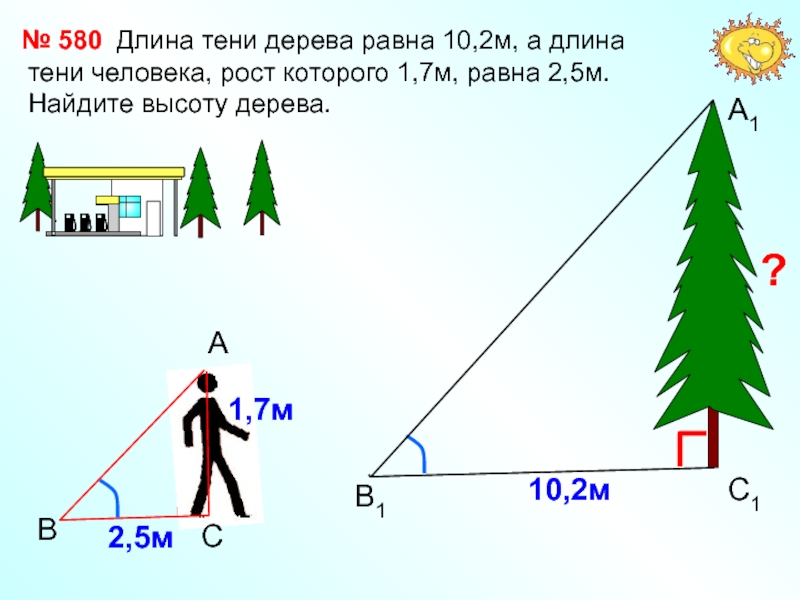
Слайд 18 Длина тени дерева равна
10,2м, а длина тени человека, рост которого 1,7м, равна 2,5м.
Найдите высоту дерева.№ 580
?
1,7м
2,5м
10,2м
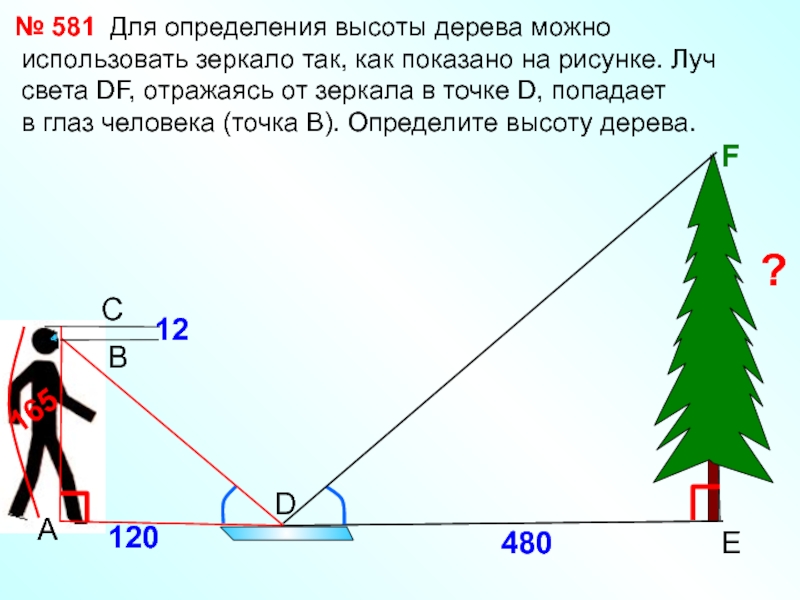
Слайд 19D
Для определения высоты дерева
можно использовать зеркало так, как показано на рисунке. Луч света
DF, отражаясь от зеркала в точке D, попадаетв глаз человека (точка В). Определите высоту дерева.
№ 581
?
165
F
E
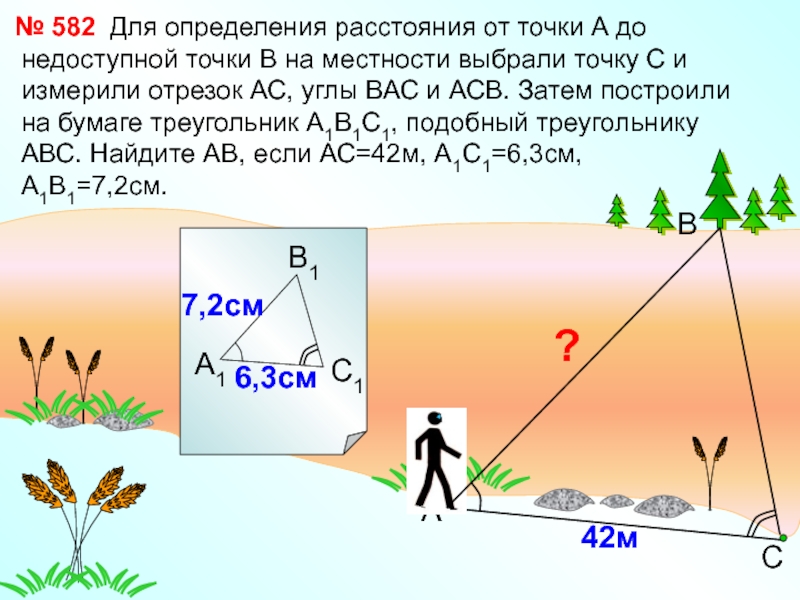
Слайд 20 Для определения расстояния от
точки А до недоступной точки В на местности выбрали точку
С и измерили отрезок АС, углы ВАС и АСВ. Затем построили на бумаге треугольник А1В1С1, подобный треугольнику АВС. Найдите АВ, если АС=42м, А1С1=6,3см,А1В1=7,2см.
№ 582
?
42м
А
В
С
6,3см
7,2см
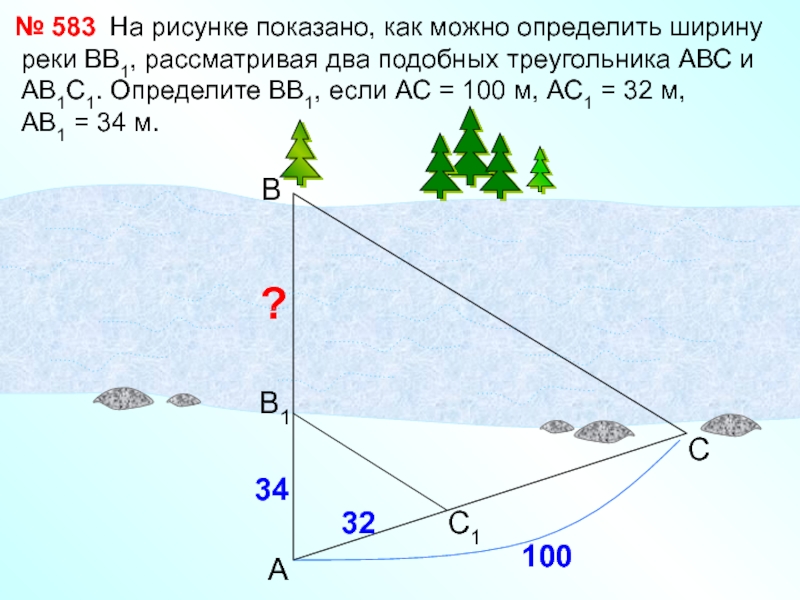
Слайд 21 На рисунке показано, как
можно определить ширину реки ВВ1, рассматривая два подобных треугольника АВС
и АВ1С1. Определите ВВ1, если АС = 100 м, АС1 = 32 м,АВ1 = 34 м.
№ 583
?
34
А
В
С
С1
В1
32
Слайд 22 Два шеста АВ и
СD разной длины а и b установлены вертикально на некотором
расстоянии друг от друга. Концы А и D, В и С соединены веревками , которые пересекаются в точке О. По данным рисунка докажите, чтоНайдите х и
докажите, что х
не зависит от а
и b.
№ 612
d
А
D
С
O
b
a
B