Слайд 2Греческие колонии в 550 г. до н.э.
(Средиземноморье)
Слайд 3Греческие колонии в 240 г. до н.э.
Слайд 4Римская империя в 150 г до н.э.
Слайд 5Греция: зарождение науки астрономия
Слайд 6 Астрономия Древней Греции — астрономические познания и взгляды
тех людей, которые писали на древнегреческом языке, независимо от географического
региона: сама Эллада, эллинизированные монархии Востока, Рим или ранняя Византия. Охватывает период с VI века до н. з. по V век н. э.
Древнегреческая астрономия является одним из важнейших этапов развития не только астрономии как таковой, но и науки вообще. В трудах древнегреческих учёных находятся истоки многих идей, лежащих в основании науки последующего времени. Между современной и древнегреческой астрономией существует отношение прямой преемственности, в то время как наука других древних цивилизаций оказала влияние на современную только при посредничестве греков.
Введение
Слайд 7
1 подход:
В древней Греции выработались два принципиально различных философских подхода
в науке вообще и астрономии в частности.
Для первого (называемого
ионическим) характерны попытки найти материальную первооснову бытия, изменением которой философы надеялись объяснить всё многообразие природы. В движении небесных тел эти философы пытались увидеть проявления тех же сил, что действуют и на Земле. К числу ионийцев относятся Фалес, Анакимандр, Анаксимен, Анаксагор, Демокрит и др.
Два подхода в древней греческой астрономии
Слайд 82 подход:
Второе направление (назыаемое италийским) основал Пифагор.
Оно видело основу
мира в математической гармонии, точнее, в гармонии чисел, стремясь при
этом к единению науки и религии. Небесные светила считались богами. Это обосновывалось следующим образом: боги — это совершенный разум, для них характерен наиболее совершенный вид движения; таковым является движение по окружности. Небесные тела движутся по окружностям, следовательно, они являются богами. Наследником пифагорейцев был Платон, который полагал весь Космос созданным идеальным божеством по своему образу и подобию.
Слайд 9Карта Земли в 6 веке до н.э.
Земля еще представляется плоской
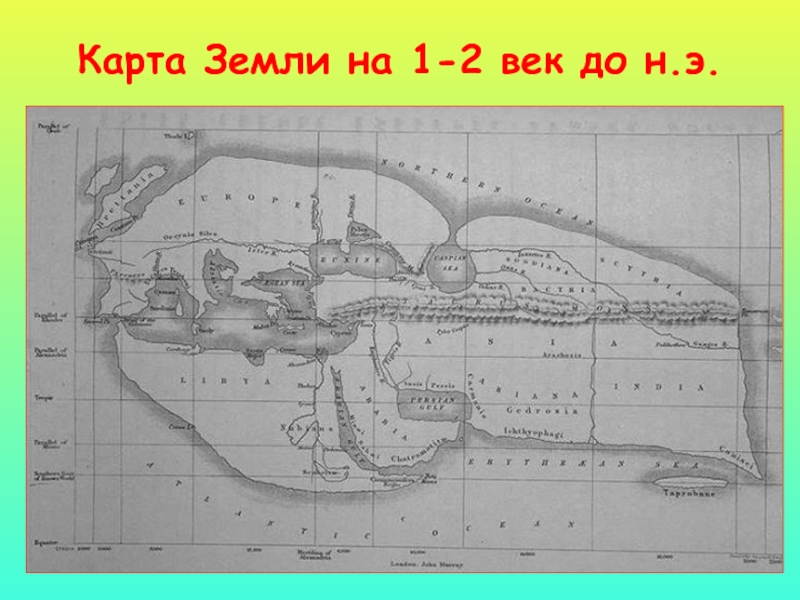
Слайд 11Карта Земли в 1-2 веках н.э.
(времена Птолемея)
Идея о сферической
форме Земли
получила признание
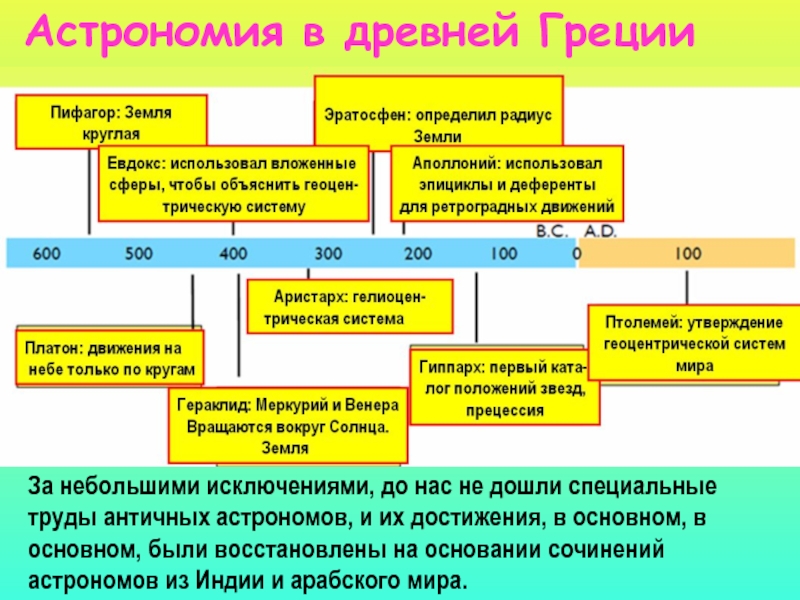
Слайд 12Астрономия в древней Греции
За небольшими исключениями, до нас не
дошли специальные
труды античных астрономов, и их достижения, в основном,
в
основном, были восстановлены на основании сочинений
астрономов из Индии и арабского мира.
Слайд 13Афинская школа — фреска художника Рафаэля, изображающая величайших мыслителей Древней
Греции
Слайд 14Библиотека, частично сгоревшая при Юлии Цезаре и восстанов-
ленная Марком Антонием,
была умышленно уничтожена толпой
христиан по приказу римского императора Феодосия
в 391 году
н. э.
Главный зал
Александрийской
библиотеки,
которая была
создана в 400 г.
до н.э.
Содержала более
500 тысяч книг,
включая и труды
греческих ученых.
Слайд 15Созвездие Ориона — одно из самых первых созвездий, упоминаемых в древнегреческой
литературе (Геосиб, поэма Труды и дни).
Слайд 16Одним из выдающихся древнегреческих
мыслителей был Гераклит Эфесский
(ок. 530—470
гг. до н.э.). Это ему принадлежат слова:
“Мир, единый из
всего, не создан никем из богов и никем из
людей, а был, есть и будет вечно живым огнем, закономерно воспламеняющимся и закономерно угасающим…”
Астрономия Гераклит была очень несовершенной. Вселенная
Вселенная делится на две части — верхнюю, небесную сферу
божественного, чистого и разумного огня, и нижнюю, подлунную сферу погасшего
вещества, холодного, тяжелого и сырого. Земля, вероятно, представлялась
Гераклиту плоской, окруженной водой. От земли и воды поднимаются испарения:
сухие, восходящие к небу и питающие собой солнце и звезды, влажные и темные,
входящие в состав земной атмосферы. Различие дней и ночей и времен года
зависит от увеличения или уменьшения количества того или другого рода испарений.
Солнце зажигает сухие испарения дня, которые гаснут во влажных испарениях ночи.
Ночь есть угасший день, лето — согревшаяся зима. Небо питается землей, земля
согревается, оживляется небом. Самые светила небесные суть подобные чашам
полые сосуды, обращенные к нам своими отверстиями: в этих сосудах скопляются
сухие пары, которые зажигаются при восходе и угасают при закате. Солнце встает
новое каждый день. Фазы Луны и затмения объясняются простым поворотом
небесных сосудов.

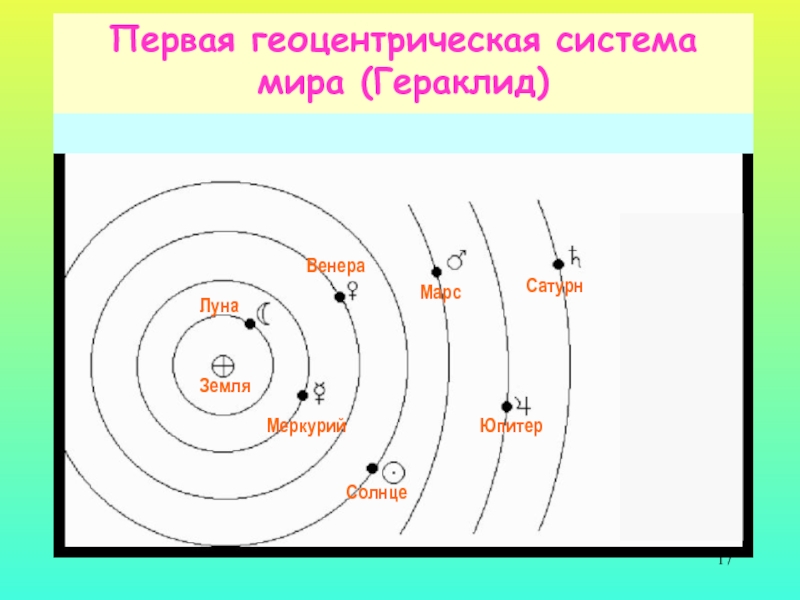
Слайд 17Первая геоцентрическая система мира (Гераклид)
Земля
Луна
Меркурий
Венера
Солнце
Марс
Юпитер
Сатурн
Слайд 18 Пифагор Самосский (ок. 580—500 гг. до н.э.) высказал
мысль
о том, что Земля, как и другие небесные тела,
имеет
форму шара. Вселенная представлялась
Пифагору в виде концентрических, вложенных друг в
друга прозрачных хрустальных сфер, к которым будто
бы прикреплены планеты.
Первая теория о порядке расположения планет
принадлежит Пифагору. В центре мира в этой модели
помещалась Земля, вокруг нее вращались сферы Луны,
Меркурия, Венеры, Солнца, Марса, Юпитера и Сатурна.
Дальше всех находилась сфера неподвижных звезд.
Пифагорейцы полагали, что Солнце расположено в том
месте космоса, которое соответствует числу семь и представляется причиной смены дня и ночи и времен года . Оно движется среди десяти сфер, вращающихся вокруг центра и Очага после сферы неподвижных звезд и пяти планет; за ним на восьмом месте находится Луна, на девятом — Земля, на десятом — Антиземля.
Пифагор открыл, что движение и обращение светил, слагающееся из их шумов, скоростей, величин, положений в созвездии, упорядочены в отношении друг друга определенной музыкальной пропорцией.
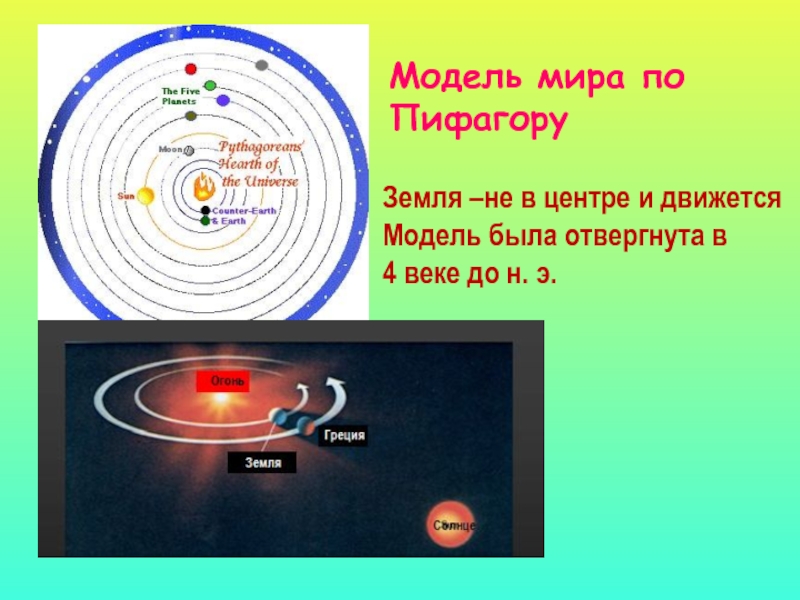
Слайд 19Модель мира по
Пифагору
Земля –не в центре и движется
Модель была
отвергнута в
4 веке до н. э.
Слайд 20Магия чисел в учении пифагорейцев
Слайд 21ФАЛЕС (ок. 625 – ок. 547 до н. э.), древнегреческий мыслитель.
Причиной солнечных
затмений считал Луну.
Предсказал солнечное затмение 28 мая 585 года
до н.э.
Фалес открыл наклон эклиптики к экватору
Определил угловую величину диаметра Луны.
Земля – плоская и плавает в океане
АНАКСАГОР (ок. 500–428 до н. э.), древнегреческий философ, математик и астроном.
Считал, что Луна светит отраженным светом от Солнца.
Лунные затмения бывают потому, что Луна попадает в тень Земле
Первым оценил размеры Земли по лунным затмениям.
Слайд 23
ПАРМЕНИД (период расцвета 504–501 до н. э.), древнегреческий философ.
У Парменида
можно встретить ряд
интересных мыслей, касающихся астрономии. Парменид первый обнаружил, что Земля шаровидна и находится в центре Вселенной. Он первый отметил, что вечерняя и утренняя звезды — одно и то же светило. И появление человека Парменид объясняет естественным образом: «Род человеческий первое начало свое имеет от солнца, но жар и холод, из которых все состоит, сильнее и солнца».
Слайд 24ДЕМОКРИТ (род. ок. 470 или 460 до н. э.; умер в глубокой старости) древнегреческий
философ, ввел понятие «атомы – неделимые материальные элементы». Говорил о
множественности миров.
Слайд 25ПЛАТОН (428 или 427 – 348 или 347 до н. э.),
древнегреческий философ, родоначальник европейской философии. Первым в европейской философии ввел
понятие единого Бога-Творца, которого назвал Демиургом. Вселенная по Платону создана Демиургом. Согласно древним грекам мир состоит из 5 элементов: земля, вода, вода, воздух, огонь и квинтэссенция.
«Мы должны изучать астрономию так же как математику при помощи теорем. А звездное небо исключается, если мы хотим получить истинное знание астрономии» (Платон)
Именно Платон поставил перед математиками задачу выразить видимые сложные движения планет (включая попятные движения как результат сложения нескольких простых движений, в качестве которых представлялись равномерные движения по кругу.
Слайд 26 Философия Платона сыграла отрицательную роль в развитии
греческой
астрономии: греческие астрономы практически не занимались развитием методики наблюдений и
созданием теорий, способных предсказывать те или иные небесные явления, делая акцент только на математическую (в основном, геометрическую) сторону объяснений явлений.
Но положительным моментом геометрической астрономии является концепция небесной сферы. Было принять, что явления восхода и захода светил, их кульминации действительно происходят таким образом, будто бы звезды были жёстко скреплены со сферическим небосводом, вращающимся вокруг наклонённой к земной поверхности оси. Таким образом естественно объяснялись основные особенности движений звёзд.
Другим важнейшим достижением математической астрономии классической Греции является введение представления об эклиптике — большом круге, наклонённом по отношению к небесному экватору, по которому совершает своё движение среди звёзд Солнце.
Третье достижение: основу геометрических теорий движения небесных тел древнегреческие астрономы положили следующий принцип: движение каждой планеты, Солнца и Луны является комбинацией равномерных круговых движений.

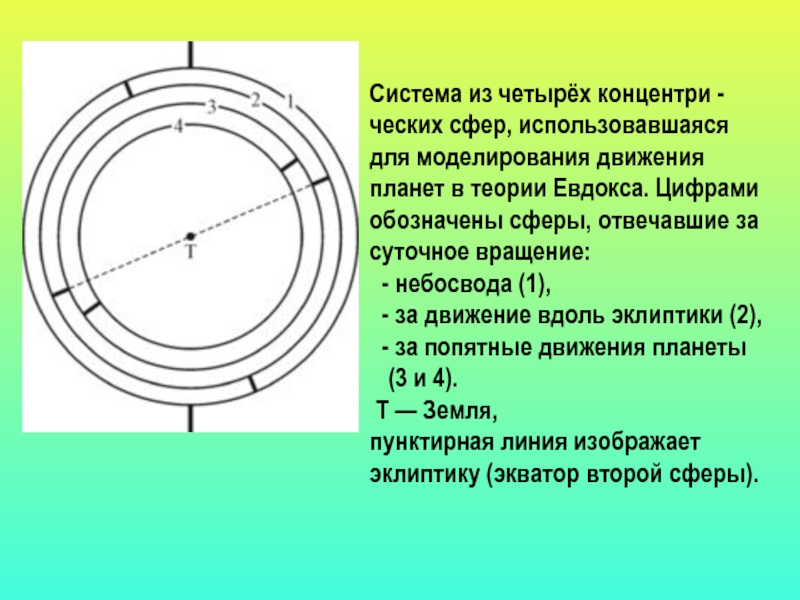
Слайд 27400до н.э. Евдокс объяснил попятное движение планет, предполагая вращение сфер
в обратном направлении. Высказал идею о геоцентрической модели Вселенной, в
которой вокруг Земли вложены одна в другую сферы.
Попятное движение
Марса
Слайд 28Система из четырёх концентри - ческих сфер, использовавшаяся для моделирования
движения планет в теории Евдокса. Цифрами обозначены сферы, отвечавшие за
суточное вращение:
- небосвода (1),
- за движение вдоль эклиптики (2),
- за попятные движения планеты
(3 и 4).
T — Земля,
пунктирная линия изображает
эклиптику (экватор второй сферы).
Слайд 29 АРИСТОТЕЛЬ (384–322 до н. э.), древнеревнегреческий философ.
Обосновал шарообразность Земли. Считал, что Земля находится в центре
мира. Отрицал вращение Земли,
Аристотель и Платон
Философ обосновал идею о том, что во Вселенной есть особая точка - центр, к которому в силу своей природы стремились тяжелые элементы: земля и вода. Ведь если бы такого центра не было, падение предметов продолжалось бы вечно, без остановки. Из-за стремления элементов к центру мира Земля получила форму шара. Лёгкие элементы - воздух и огонь – напротив, стремились от центра, но не уходили за границы "подлунной сферы". За ней начиналось царство небесных тел, построенное из особого, пятого, элемента - "квинтэссенции", эфира.
Слайд 30
Aристотель воспринял многие идеи у своего учителя Платона:
1)
Земля не совершенна и изменчива
2) Небеса совершенны и неизменны
3) Наиболее
совершенная геометрическая фигура
- сфера
4) Естественное движение сферы это вращение
5) Небеса должны состоять из вращающихся
сфер.
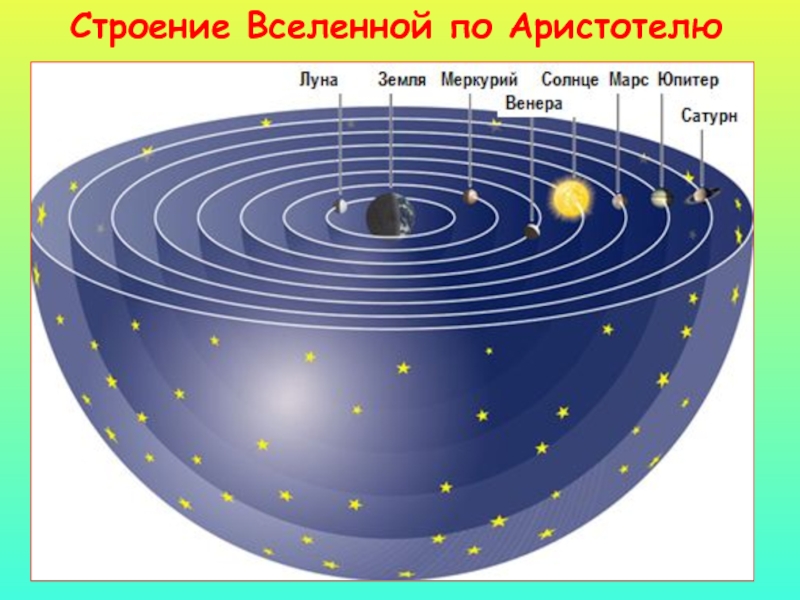
Слайд 31Строение Вселенной по Аристотелю
Слайд 32АРИСТАРХ САМОССКИЙ (320 – около 250 до н. э.), древнегре-
ческий астроном.
1)
Первым высказал идею гелиоцентризма -
центрального положения Солнца, находяще-
гося в центре
сферы неподвижных звезд.
2) Впервые попытался рассчитать расстояние
до Луны и Солнца и их размеры. Метод,
который применял Аристарх, был первым
определением расстояний до небесных
объектов с помощью наблюдений.
3) Исходя из гелиоцентрической системы и ненаблюдаемости годичных параллаксов звёзд, Аристарх сделал пионерский вывод, что расстояние от Земли до Солнца пренебрежимо мало по сравнению с расстоянием от Солнца до звёзд
Труд Аристарха «О размерах и расстояниях Солнца и Луны»
Слайд 33Важное замечание
В эти времена ученые еще не использовали понятия
тригонометрических
функций (синуса, косинуса и др.).
Вместо них использовались понятия «хорда».
Связь
этих понятий
Приведена на рисунке.
Соотношение между длинами
хорд и соответствующими
углами обычно греками
приводится в специальных
таблицах.
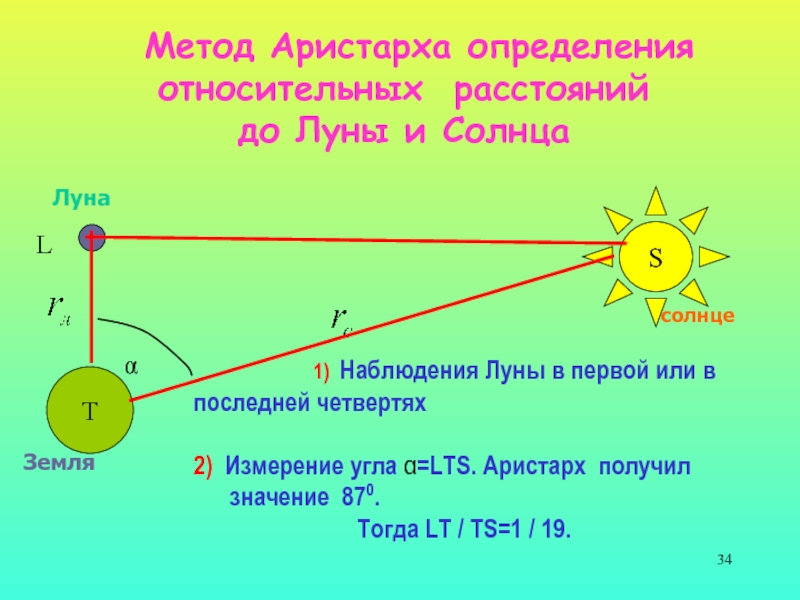
Слайд 34 Метод Аристарха определения относительных расстояний до
Луны и Солнца
T
S
солнце
Луна
Земля
L
1) Наблюдения Луны в первой или в
последней четвертях
2) Измерение угла α=LTS. Аристарх получил
значение 870.
Тогда LT / TS=1 / 19.
α
Слайд 35Сравнение с современными данными
Современные данные:
Расстояние до Солнца Аристарх недооценил примерно
в 20 раз.
Причина ошибки заключалась в том, что момент
лунной
квадратуры может быть установлен только с очень большой
неопределённостью, которая ведёт к неопределённости значения
угла α и, следовательно, к неопределённости расстояния до
Солнца. Современное значение угла 89о51’.
Слайд 36Определение размеров Солнца и Луна
Для этого Аристарх привлекает анализ
лунных затмений. Причина затмений ему совершенно ясна: они происходят тогда,
когда Луна попадает в конус земной тени.
По его оценкам, в районе лунной орбиты ширина этого конуса в 2 раза больше диаметра Луны.
Зная это значение, Аристарх с помощью довольно остроумных построений и выведенного ранее отношения размеров Солнца и Луны заключает, что отношение радиусов Солнца и Земли таково:
3) Был оценён также радиус Луны: по Аристарху, он примерно в три раза меньше радиуса Земли, что не так уж и далеко от правильного значения (3/11 радиуса Земли, всего на 6 % меньше значения Аристарха).
Слайд 37Схема, поясняющая определение радиуса Луны по методу Аристарха (византийская копия
Х века)
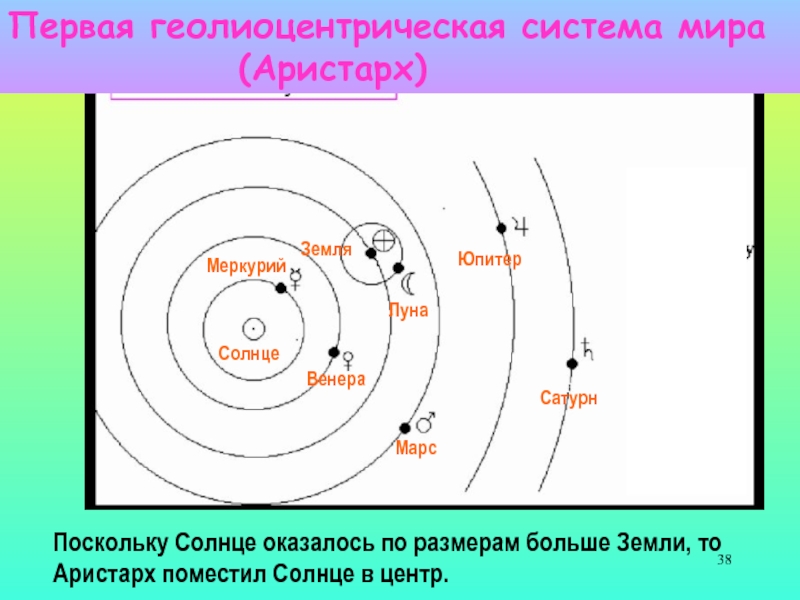
Слайд 38Первая геолиоцентрическая система мира
(Аристарх)
Солнце
Меркурий
Венера
Земля
Луна
Юпитер
Марс
Сатурн
Поскольку
Солнце оказалось по размерам больше Земли, то
Аристарх поместил Солнце в центр.
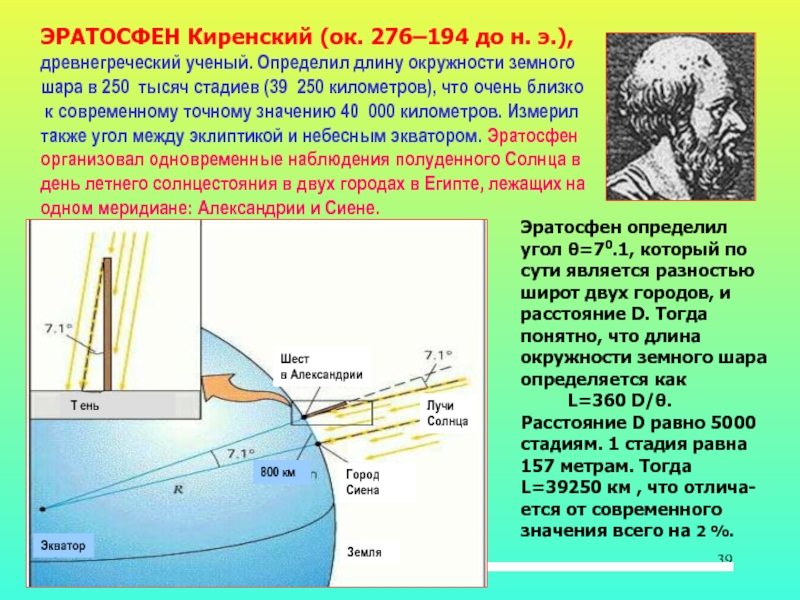
Слайд 39ЭРАТОСФЕН Киренский (ок. 276–194 до н. э.),
древнегреческий ученый. Определил длину окружности земного
шара в 250 тысяч стадиев (39 250 километров), что очень близко
к
современному точному значению 40 000 километров. Измерил
также угол между эклиптикой и небесным экватором. Эратосфен
организовал одновременные наблюдения полуденного Солнца в
день летнего солнцестояния в двух городах в Египте, лежащих на
одном меридиане: Александрии и Сиене.
Эратосфен определил угол θ=70.1, который по сути является разностью широт двух городов, и расстояние D. Тогда понятно, что длина
окружности земного шара определяется как
L=360 D/θ. Расстояние D равно 5000 стадиям. 1 стадия равна 157 метрам. Тогда L=39250 км , что отлича- ется от современного значения всего на 2 %.
Шест
в Александрии
Лучи
Солнца
Земля
Экватор
800 км
Т ень
Город
Сиена
Слайд 40ГИППАРХ (ок. 180 или 190 – 125 до н. э.), древнегреческий астроном.
Занимался систематическими наблюдениями небесных светил.
1) Первым ввел географические координаты
– широту и долготу.
2) «Улучшил методику расчета видимого движения Солнца и Луны, предположил, что Земля смещена от центра окружности, по которой вращается Солнце.
3) Определил продолжительность года.
4) Используя наблюдения солнечного затмения 129 года до н.э., определил расстояние до Луны с большой точностью и расстояние до Солнца.
5) Уточнил синодический месяц.
6) Составил звездный каталог из 850 звезд, зафиксировал их яркость при помощи введенной им шкалы звездных величин.
7) Открыл прецессию земной оси.
На глобусе этой скульптуры приведены результаты
работ Гиппарха.
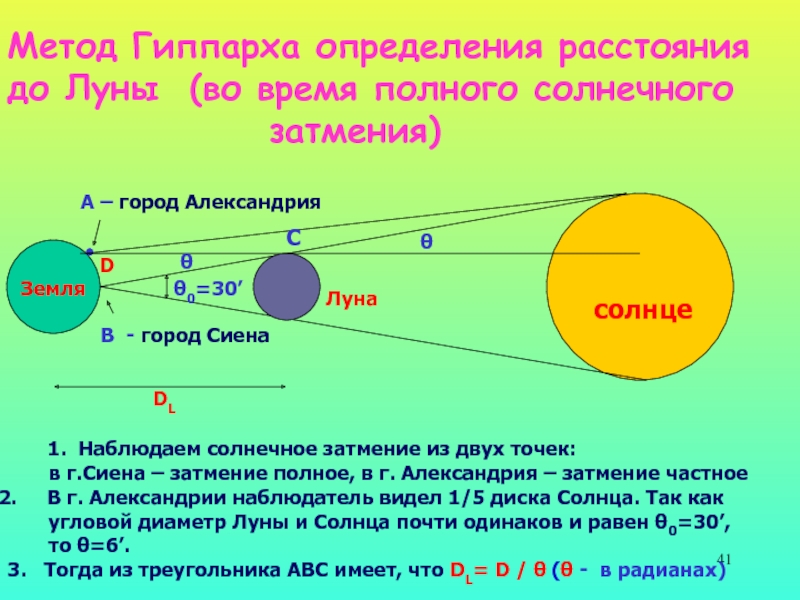
Слайд 41Метод Гиппарха определения расстояния
до Луны (во время полного солнечного
затмения)
.
А – город Александрия
В - город Сиена
1. Наблюдаем солнечное затмение из двух точек:
в г.Сиена – затмение полное, в г. Александрия – затмение частное
В г. Александрии наблюдатель видел 1/5 диска Солнца. Так как
угловой диаметр Луны и Солнца почти одинаков и равен θ0=30’,
то θ=6’.
3. Тогда из треугольника АВС имеет, что DL= D / θ (θ - в радианах)
θ0=30’
θ
солнце
Луна
Земля
θ
DL
D
С
Слайд 42Метод Гиппарха определения расстояния до Луны (во время полного солнечного
затмения)
4. Оценим точность результата. Величина D равна 5000 стадиям.
Тогда
Настоящее значение
расстояния до Луны равно
406 700 км – в апогее
356 400 км – в перигее
384 400 км - среднее
Слайд 43В 133 г. до н. э. в созвездии Скорпиона вспыхнула
новая звезда. По сообщению Плиния, это событие побудило Гиппарха составить
звёздный каталог, чтобы зафиксировать изменения в сфере "неизменных звёзд".
Сравнив свои результаты с координатами некоторых звёзд, измеренными Аристилом и Тимохарисом (современниками Аристарха Самосского), Гиппарх обнаружил, что эклиптические долготы увеличились одинаково, а широты не изменились. Из этого он сделал вывод, что дело не в движении самих звёзд, а в медленном смещении небесного экватора.
Так Гиппарх открыл, что небесная сфера кроме суточного движения ещё очень медленно поворачивается вокруг полюса эклиптики относительно экватора (точный период 25 735 лет). Это явление он назвал прецессией (предварением равноденствий).
Гиппарх и открытие прецессии
(первая попытка)
Слайд 44Гиппарх и открытие прецессии
(вторая попытка)
С 162 по 128 годы до
н.э. Гиппарх наблюдал 9 солнцестояний
Результаты он
сравнивал с результатами Аристарха, полученные
100 лет назад.
Тропический год (S) это промежуток времени, по истечении
которого Солнце возвращается в точку солнцестояния (или равноденствия). Гиппарх получил значение
S = 365d 5h 55m 12s ( Гиппарх ошибся на 6m)
Звездный год (Т) это промежуток времени, по истечение которого Солнце возвращается в одно и то же положение относительно
звезд
Гиппарх нашел, что между T и S есть различие: T – S = 20m .
Он правильно объяснил, что точка весеннего равноденствия
смещается навстречу движению Солнца.
Скорость смещения по Гиппарху равна 36” / год
Современное значение 360о / 26 000 лет=50” / год
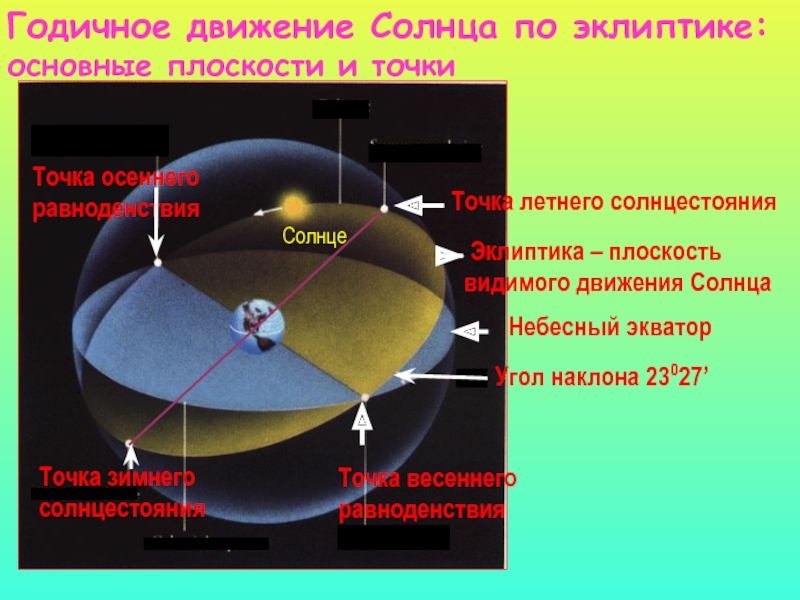
Слайд 45Годичное движение Солнца по эклиптике:
основные плоскости и точки
Эклиптика –
плоскость
видимого движения Солнца
Точка зимнего
солнцестояния
Угол наклона 23027’
Точка весеннего
равноденствия
Небесный
экватор
Точка летнего солнцестояния
Точка осеннего
равноденствия
Солнце
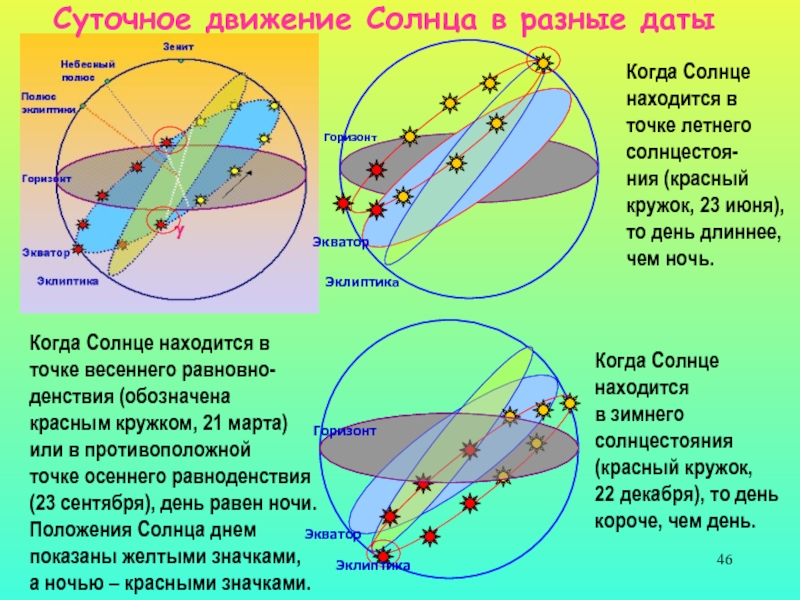
Слайд 46Когда Солнце находится в
точке весеннего равновно-
денствия (обозначена
красным кружком,
21 марта)
или в противоположной
точке осеннего равноденствия
(23 сентября), день
равен ночи.
Положения Солнца днем
показаны желтыми значками,
а ночью – красными значками.
Когда Солнце
находится в
точке летнего
солнцестоя-
ния (красный
кружок, 23 июня),
то день длиннее,
чем ночь.
Когда Солнце
находится
в зимнего
солнцестояния
(красный кружок,
22 декабря), то день
короче, чем день.
Горизонт
Экватор
Эклиптика
Горизонт
Экватор
Эклиптика
Суточное движение Солнца в разные даты
Слайд 47Неравномерность движения
Солнца по эклиптике
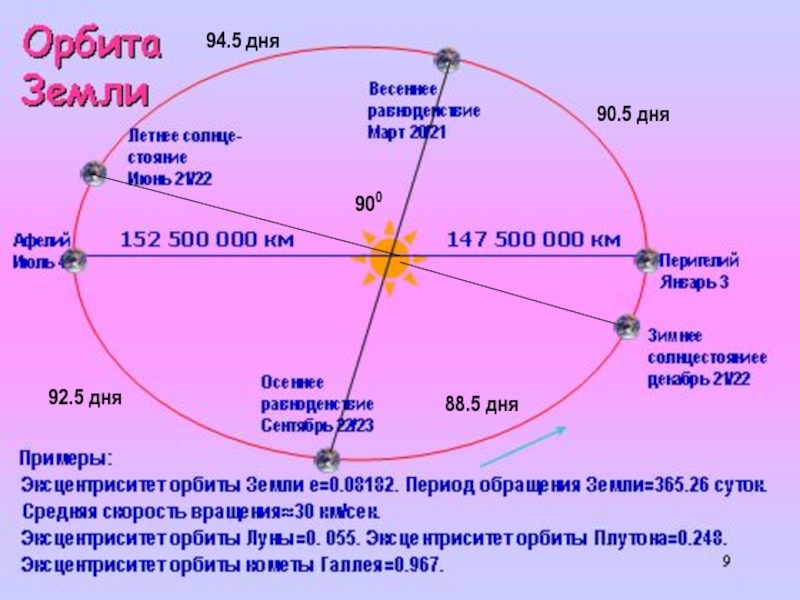
Слайд 4894.5 дня
88.5 дня
90.5 дня
92.5 дня
900
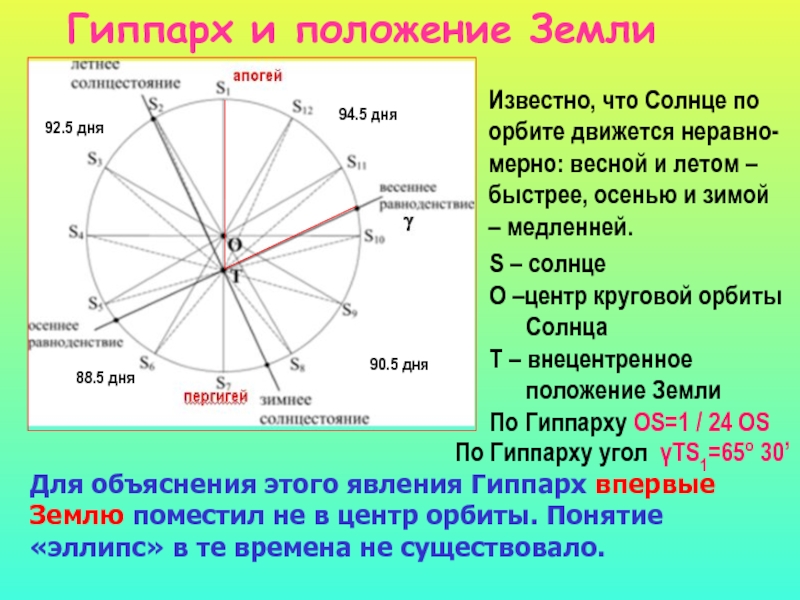
Слайд 49Гиппарх и положение Земли
S – солнце
О –центр круговой орбиты
Солнца
T – внецентренное
положение Земли
По Гиппарху ОS=1 / 24 ОS
Известно, что Солнце по
орбите движется неравно-
мерно: весной и летом –
быстрее, осенью и зимой
– медленней.
Для объяснения этого явления Гиппарх впервые Землю поместил не в центр орбиты. Понятие «эллипс» в те времена не существовало.
По Гиппарху угол γТS1=65о 30’
94.5 дня
92.5 дня
88.5 дня
90.5 дня
Слайд 50
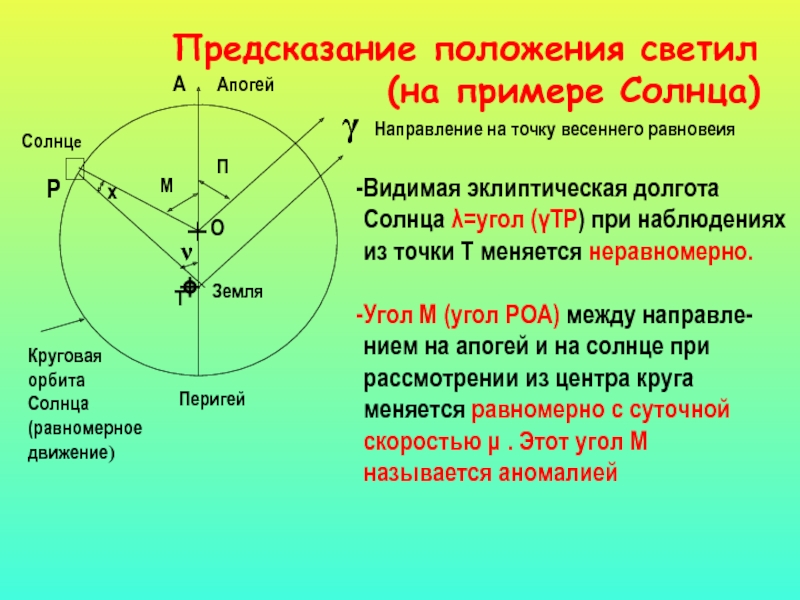
+
Предсказание положения светил
(на примере Солнца)
?
⌖
Круговая
орбита
Солнца
(равномерное
движение)
Р
Солнце
Т
Земля
Апогей
γ
О
П
М
ν
х
Видимая эклиптическая долгота
Солнца λ=угол (γТР) при наблюдениях
из точки Т меняется неравномерно.
Угол М (угол РОА) между направле-
нием на апогей и на солнце при
рассмотрении из центра круга
меняется равномерно с суточной
скоростью μ . Этот угол М
называется аномалией
А
Направление на точку весеннего равновеия
Перигей
Слайд 51
+
Предсказание положения светил
(на примере Солнца)
?
⌖
Круговая
орбита
Солнца
(равномерное
движение)
Р
Солнце
Т
Земля
Апогей
γ
О
П
М
ν
х
А
«средняя
долгота»
- аномалия
Из треугольника ТРО имеем:
- среднее
суточное
движение
Слайд 52
+
Предсказание положения светил
(на примере Солнца)
?
⌖
Круговая
орбита
Солнца
(равномерное
движение)
Р
Солнце
Т
Земля
Апогей
γ
О
П
М
ν
х
А
Мы получили уравнение с тремя
неизвестными:
Если провести определения трех наблюдаемых долгот λ в трех моментах времени t, можно определить эти неизвестные. Птолемей этим
методом получил:
Слайд 53Предсказание положения светил
(на примере Солнца)
В современном виде соотношение Гиппарха
записывается
так:
Теория движения по эллипсу дает следующее:
е – эксцентриситет эллипса, причем
Слайд 54Предсказание положения светил
(на примере Солнца)
3) Итак:
- Гиппарх
-теория эллиптического
движения
- ошибка
Если взять эксцентриситет Земной орбиты то ошибка в
определении долготы Солнца составит всего 43”
Вывод: теория Гиппарха дает хорошую точность при
определении видимой долготы Солнца.
Но для определения расстояния до планет этот метод дает
плохую точность (см. метод Птолемея)
Слайд 55Основные выводы из модели
солнечного движения
(по Гиппарху)
1. В движение Солнца
есть одна переменная величина – скорость
движения по эклиптике
2. Апогей находится
в направлении минимальной скорости по
эклиптике, а перигей – в направлении быстрого движения
3. Направление на апогей всегда равно 65.5 градуса по отношению
к точке весеннего равноденствия
Слайд 56
ПТОЛЕМЕЙ Клавдий (ок. 90 – ок. 160), древнегреческий ученый, последний крупный астроном
античности. Дополнил звездный каталог Гиппарха. Соорудил специальные астрономические нструмен-
ты: астролябию,
армилярную сферу, трикветрум. Описал положение 1022 звезд. Разработал математическую теорию
движения планет вокруг неподвижной Земли , позволявшую вычислить их положение на небе. Достигнул высокой по тем временам точности. Но теория, тем не менее, не объясняла изменение блеска Марса и другие парадоксы античной астрономии.
Основной труд Птолемея – это «Математический синтаксис»
или «АЛЬМАГЕСТ»
Слайд 57Представления о Земле во времена Птолемея
Слайд 58Трикветрум Клавдия Птолемея (из книги 1544 г.)
При своих исследованиях Птолемей
опирался и на свои наблюдения.
Но следует сказать, что до сих
пор
идет дискуссия о том, что на самом
деле Птолемей подгонял свои
наблюдения по свою теорию.
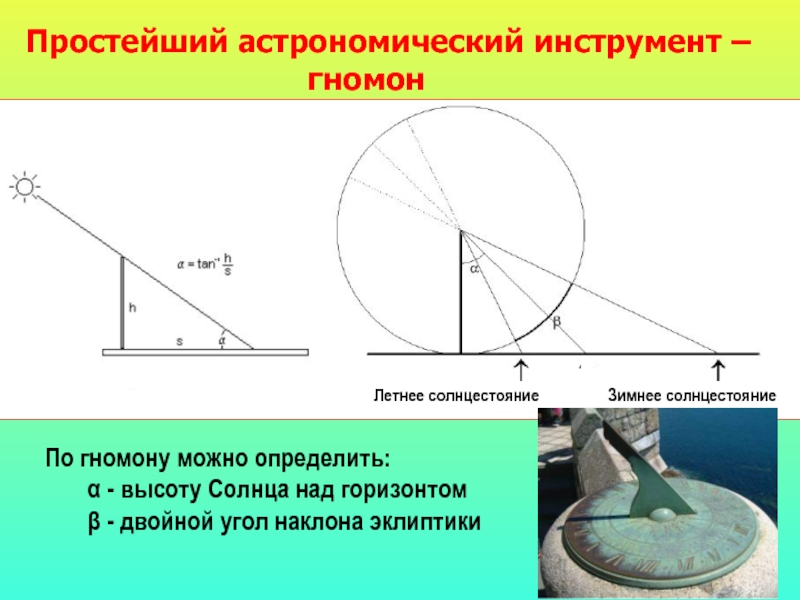
Слайд 59 Простейший астрономический инструмент –
гномон
Летнее солнцестояние Зимнее солнцестояние
По гномону можно определить:
α - высоту Солнца над горизонтом
β - двойной угол наклона эклиптики
Слайд 60Альмагест
Это весьма обширное
сочинение— занимает более
600 страниц большого формата.
«Альмагест» был разделен
самим Птолемеем" на 13 книг.
Книга 1
— вводная. В ней
утверждается, что небесный
свод движется как единая сфера.
Земля шарообразна и
неподвижна, находится в центре небесной сферы и имеет по сравнению с ней ничтожно малые (точечные) размеры. В книге приводятся основы птолемеевой сферической тригонометрии, дается ряд полезных таблиц, а также описание» некоторых простых угломерных приборов.
Иллюстрация из Альмагеста
Слайд 61Альмагест
В книге II приводится решение
некоторых общих задач сферической
астрономии.
В книге III рассматриваются движение
Солнца по эклиптике и солнечная
аномалия (происходящая от неравно-
мерности движения Земли вокруг Солнца по эллиптической орбите). Вводятся понятия об эксцентре и эпицикле.
В книге IV описывается видимое движение Луны и его аномалии.
В книге V Птолемей строит свою теорию движения Луны, основанную на комбинации нескольких круговых движений.
Слайд 62Альмагест
Книга VI посвящена теории солнечных .и лунных затмений, базирующейся на
расчетах моментов сизигий (новолуний и полнолуний), а также особенностях движения
Луны, связанных с тем, что ее орбита наклонена к плоскости эклиптики на небольшой угол (5°). Здесь же приведены таблицы затмений.
В VII и VIII книгах приводятся описания созвездий, видимых с территории Греции и Александрии, и, кроме того, каталог звезд, составленный Птолемеем на основе собственных наблюдений и наблюдений Гилпарха {II век до н.э.). В этом каталоге даны положения 1025 звезд.
Слайд 63Предпосылки для Птолемея: (1) что такое год
Есть определения:
1) возвращение Солнца на эклиптике к той же звезде
(звездный год)
2) возвращение Солнца к точке с одинаковым склонением,
т.е возвращение Солнца к одинаковому положению на
экваторе (тропический год)
3) возвращение Солнца к точке, где скорость стала
одинаковой (аномалистический год)
4) возвращение Солнца в точку с одинаковой широтой, т.е.
к одинаковому расстоянию от эклиптики.
Птолемей (как и Гиппарх) выбрал второй вариант – возвращение
Солнца в точку весеннего равноденствия.
Слайд 64Предпосылки для Птолемея:
(2) длительность года
Гиппарх на основе данных нахождения
Солнца в точке
летнего солнцестояния в интервале 280 – 135 г.
до н.э.
получил 365+1/4-1/300 ( =365.2467 дня). Современное значение
тропического года =365.2422 дня.
Птолемей, на основе наблюдений в 132, 139 и 140 гг. н.э.
получил то же значение. Это значение всего на 6.5 минут
отличается от современного.
Слайд 65Каждая из планет (кроме Меркурия) равномерно движется по малому кругу
(эпициклу), центр которого совершает движение по большому кругу (деференту), причём
Земля смещена относительно центра деферента; самое главное, и угловая, и линейная скорость центра эпицикла меняется при движении по деференту, причём это движение выглядело бы равномерным при наблюдении из некоторой точки (эквант), так что отрезок, соединяющий Землю и эквант делится центром деферента пополам. Эта теория позволяла с большой точностью смоделировать зодиакальное неравенство (неравномерность вращения планет по эклиптике) в движении планет.
Планетная теория Птолемея
(теория бисекции)
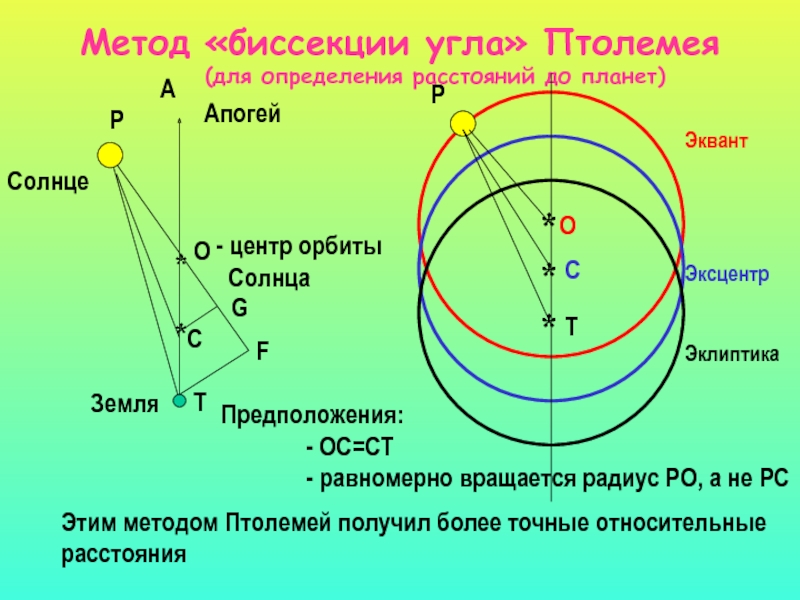
Слайд 66Метод «биссекции угла» Птолемея
(для определения расстояний до планет)
*
*
*
*
*
А
Апогей
Р
Солнце
Т
Земля
О
С
G
F
О
С
Т
Эквант
Эксцентр
Эклиптика
P
Предположения:
- ОС=СТ
- равномерно вращается радиус РО, а не РС
Этим методом Птолемей получил более точные относительные
расстояния
- центр орбиты
Солнца
Слайд 67Основные положения в системе
мира Птолемея
В центре
мира находится Земля.
Все планеты вращаются по эпициклам и
деферентам.
3. Комбинация относительных радиусов этих
кругов и скоростей вращения позволяет объяснить
видимые движения планет.
4. Солнце вращается только по деференту.
5. Все звезды расположены на хрустальной сфере,
которая вращается вокруг Земли.
Книга «Математический синтаксис»
(«Альмагест», примерно 127-151 г. н.э.)
Слайд 68
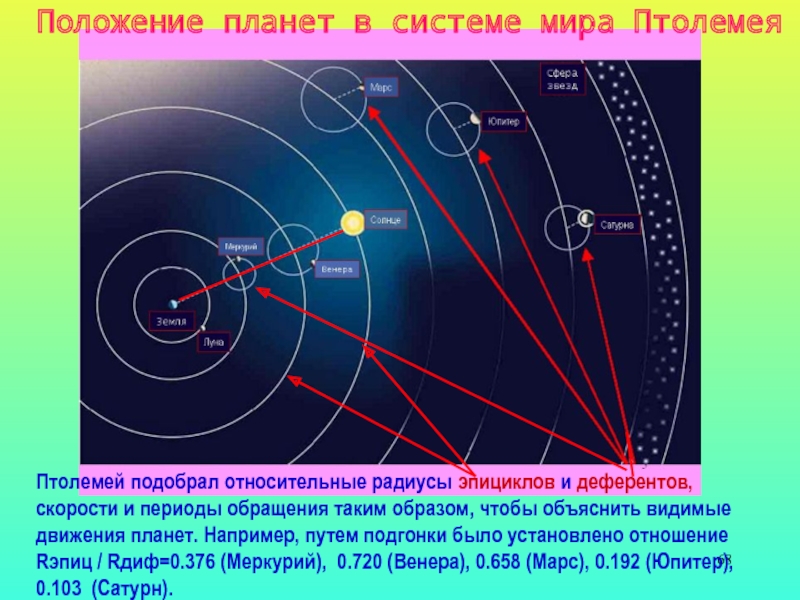
Птолемей подобрал относительные радиусы эпициклов и деферентов, скорости и периоды
обращения таким образом, чтобы объяснить видимые движения планет. Например, путем
подгонки было установлено отношение Rэпиц / Rдиф=0.376 (Меркурий), 0.720 (Венера), 0.658 (Марс), 0.192 (Юпитер), 0.103 (Сатурн).
Положение планет в системе мира Птолемея
Слайд 69-
Две особенности в системе Птолемея
(пояснения к предыдущему слайду)
Центры эпициклов
нижних планет
( Меркурий, Венера) находятся на
прямой, соединяющей Землю и
Солнце. Эта прямая на слайде
обозначена красной штриховой
линией. Этим Птолемей объясняет
колебательное движение
внутренних планет около Солнца.
Каждая из верхних планет (Марс,
Юпитер, Сатурн) находится на
эпицикле в том же направлении относительно
центра эпицикла, в каком относительно Земли находится Солнце. Другими
словами, радиусы-векторы эпициклов этих планет всегда параллельны
друг другу и линии Земля Солнца (голубые пунктирные линии).
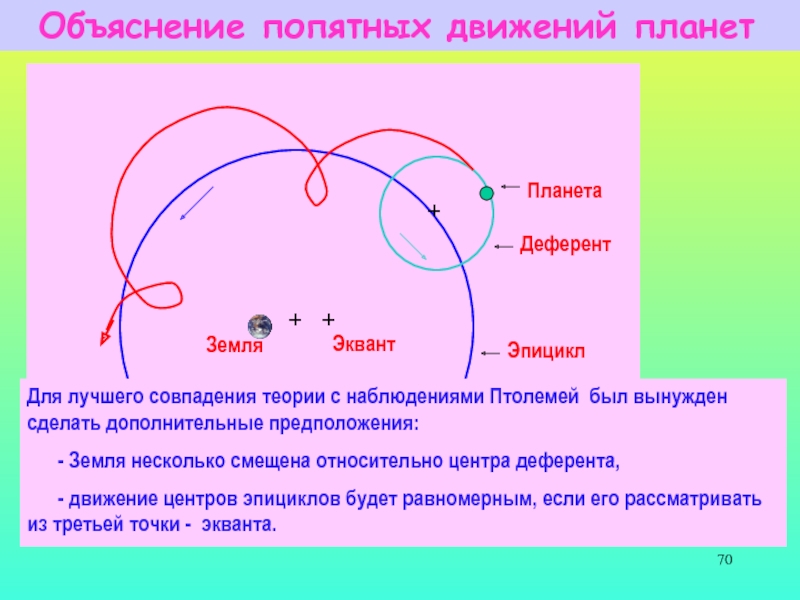
Слайд 70 Объяснение попятных движений планет
центр деферента
Для лучшего
совпадения теории с наблюдениями Птолемей был вынужден сделать дополнительные предположения:
- Земля несколько смещена относительно центра деферента,
- движение центров эпициклов будет равномерным, если его рассматривать из третьей точки - экванта.
+
+
+
Планета
Земля
Эквант
Деферент
Эпицикл
Слайд 72Вопрос: если система Птолемея ошибочна, поскольку она основывалась на ложном
представлении о неподвижной Земле как центре мироздания, то почему расчеты,
проведенные на ее основе, дают правильные результаты? Ведь именно поэтому она использовалась астрономами почти 1400 лет. Ответ на поставленный вопрос очевиден: это система кинематическая. Птолемей не объяснял (да и не мог объяснить), почему движение планеты именно такое, каким он его описывал. Но каждое движение относительно. И, как это ни парадоксально звучит, Птолемей описал и смоделировал движение каждой из планет совершенно правильно — так, как его действительно видит наблюдатель с Земли. Эпицикл верхней планеты и есть отображение движения Земли вокруг Солнца (в случае нижней планеты это ее деферент)
Слайд 73В течение почти 14 веков система мира Птолемея вполне
удовлетворительно объясняла
наблюдаемые движения
планет. При появлении расхождений теории с наблюде-
ниями с
более возросшей точностью теорию «подправ-
ляли» введением дополнительных эпициклов на эпициклах.
Ко времени Коперника (XV век) эта система уже насчиты-
вала 78 кругов (эпициклов и деферентов).
И под тяжестью таких кругов эта система в конце концов
рухнула.
Слайд 74Астрономия в древней Греции (3)
Резюме:
Высочайшими достижениями греков (Аристарх,
Эратосфен, Гиппарх
и др., 300-120 годы до н.э.) были:
создание шкалы звездных
величин,
открытие прецессии земной оси,
измерение года с ошибкой в 6 минут,
определение размеров круглой Земли,
определение относительных расстояний до Луны и Солнца,
предложение гелиоцентрической системы мира.
представление о мире как о непрерывной цепочке причин и следствий,
когда каждое явление природы является результатом внутренних процессов,
происходящих в тех или иных природных стихиях;
геометризация Вселенной: представление о том, что наблюдаемые на небе
явления есть проявление процессов, происходящих в пространстве;
* введение основных понятий сферической астрономии
* установление малости Земли по сравнению с расстоянием до звёзд