Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Development of Applied Computer Vision Systems Using Projective Morphologies and Evidence-Based Image Analysis
Содержание
- 1. Development of Applied Computer Vision Systems Using Projective Morphologies and Evidence-Based Image Analysis
- 2. FGUP “State Research Institute of Aviation Systems”
- 3. Visual Data Representation and Processing
- 4. Visual Data Representation and Processing
- 5. Two Vision Frameworks PresentedVision Framework is a
- 6. PROJECTIVE MORPHOLOGIES
- 7. MM 1. Математическая морфология Серра Обработка
- 8. MM 1. Математическая морфология СерраСтруктурирующий элемент
- 9. MM 1. Математическая морфология Серра BBTTStructuring Elements
- 10. MM 1. Математическая морфология СерраММ-операторы:ММ-проекторы:Эрозия (сжатие)Дилатация (расширение)ММ-открытиеММ-закрытиеММ-фильтры
- 11. MM 2. Бинарная морфология на базе скелетовA
- 12. MM 3. Морфологический анализ Пытьева Сравнение
- 13. MM 3. Морфологический анализ Пытьева A1A2A3A4Индикаторная функция
- 14. MM 3. Морфологический анализ Пытьева Изображение ,
- 15. MM 3. Морфологический анализ Пытьева α =
- 16. Projective Morphology as a Union of Morphologies
- 17. PROJECTORS, CLASSES OF SHAPES, MORPHOLOGICAL COMPLEXITY AND MORPHOLOGICAL SPECTRUM
- 18. Проекторы как распознающие операторы (М. Павель) Морфологический
- 19. Сравнение форм по сложности (Пытьев) M1M2M3M3 ⊆
- 20. Вложенные классы форм и идея морфологического спектра⊕⊕⊕⊕rСкачкообразное изменение площади фигуры на размер объектаXrBX◦rBXrB
- 21. PSX(r,B) = - ∂S(X◦rB)/∂r, r≥0, (1)PSX(-r,B) =
- 22. Построение морфологического спектра в непрерывной бинарной морфологии
- 23. Дискретно-непрерывный морфологический спектр силуэтов животных с реальных изображений (Визильтер, Сидякин, 2010)
- 24. СЕГМЕНТАЦИЯ + РЕКОНСТРУКЦИЯ (поиск нетривиальных описаний и построение морфологических систем из готовых «кубиков»)
- 25. Формальная морфологияϑΛM ⊆ ϑεδϕεδ = δεмножество образовмножество
- 26. Сегментация + Реконструкциямножество образовмножество описанийИскусственныйизоморфизмЕстественныйгомоморфизм568=5×102+6×101+8×1040=1×25+1×2328=22 × 71f(x)
- 27. Способ описания формы: Преобразование Хафа (HT)Голосование точек
- 28. Способ описания формы: Обобщенное преобразование Хафа (GHT)+
- 29. Морфологии Серра на базе преобразования Хафа и
- 30. Морфология на базе локального преобразования ХафаTransformThresholdingReconstructionEdge
- 31. Морфология на базе локального преобразования ХафаTransformThresholdingReconstructionEdge
- 32. Выделение линеаментов различных размеров
- 33. Морфологии из «готовых кубиков» Идея: Построение различных
- 34. Селективные морфологии(a)(b)(c)(a)(b)(a)(a)Открытие MM(a)(a) O(Object)=∅, if E(Object) =
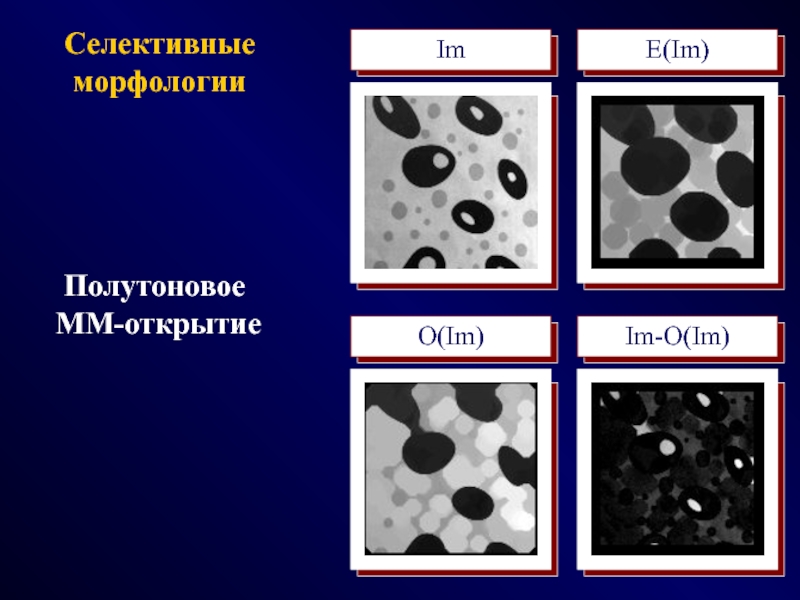
- 35. Селективные морфологииImE(Im)O(Im)Im-O(Im)Полутоновое MM-открытие
- 36. Селективные морфологииПолутоновое SM-открытиеImE(Im)SO(Im)Im-SO(Im)
- 37. Селективные морфологииImD(Im)C(Im)Im-C(Im)Полутоновое MM-закрытие
- 38. Селективные морфологииImD(Im)SC(Im)Im-SC(Im)Полутоновое SM-закрытие
- 39. Селективные морфологииПолутоновое MM-открытиеImE(Im)O(Im)Im-O(Im)
- 40. Селективные морфологииПолутоновое SM-открытиеImE(Im)SO(Im)Im-SO(Im)
- 41. Селективные морфологииПолутоновое MM-закрытиеImD(Im)C(Im)Im-C(Im)
- 42. Селективные морфологииПолутоновое SM-закрытиеImD(Im)SC(Im)Im-SC(Im)
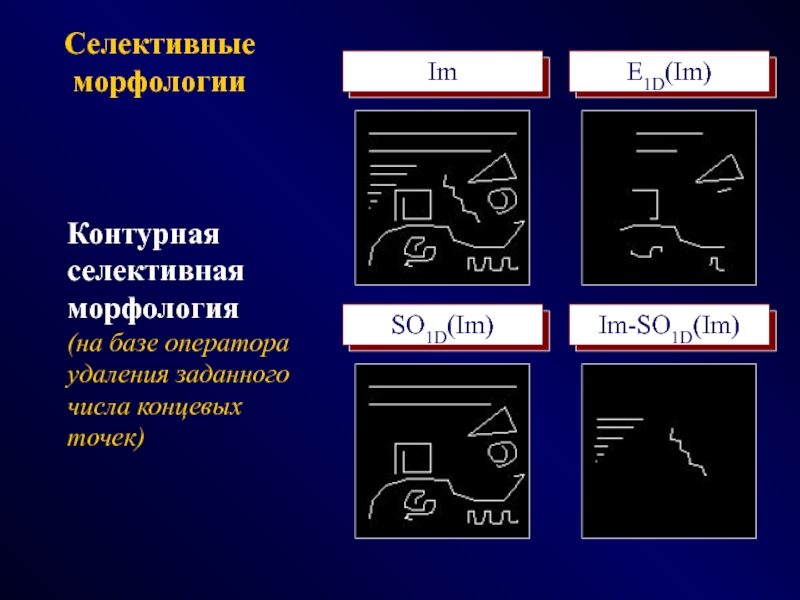
- 43. Селективные морфологииImE1D(Im)SO1D(Im)Im-SO1D(Im)Контурная селективная морфология(на базе оператора удаления заданного числа концевых точек)
- 44. МОРФОЛОГИЧЕСКИЕ АЛГЕБРЫ, ПРОСТРАНСТВА РАЗЛОЖЕНИЙ И СЕГМЕНТАЦИЯ КАК РЕГУЛЯРИЗАЦИЯ
- 45. Морфологические алгебры
- 46. Проективные морфологические разложенияПроективные морфологические разложения Использование
- 47. Проективные морфологические разложенияТипы морфологических разложенийУсловие разложимости:∃ E⊆Ω: Pr(A,E) = Vk=1..n(Pr(A,Ek)) = Vk=1..n(r(A,Ek)∙Ek)
- 48. Проективные морфологические разложенияОртогональные морфологии на базе БПФ и т.п.БПФ, ДКП, фильтры НЧ, ВЧВейвлет-преобразование и фильтры
- 49. Проективные морфологические разложения Морфологический анализ изображений
- 50. Проективные морфологические разложения Морфологический анализ изображений Фильтрация изображений с использованием разложений:
- 51. Проективные морфологические разложения Морфологический анализ изображений Структурное
- 52. Проективные морфологические разложения Конструирование алгоритмов обнаружения объектов Обнаружение объектов с использованием разложений:
- 53. Проективные морфологические разложения Морфологические операторы сегментации и сжатия данных Морфологическая сегментация на базе проективных разложений
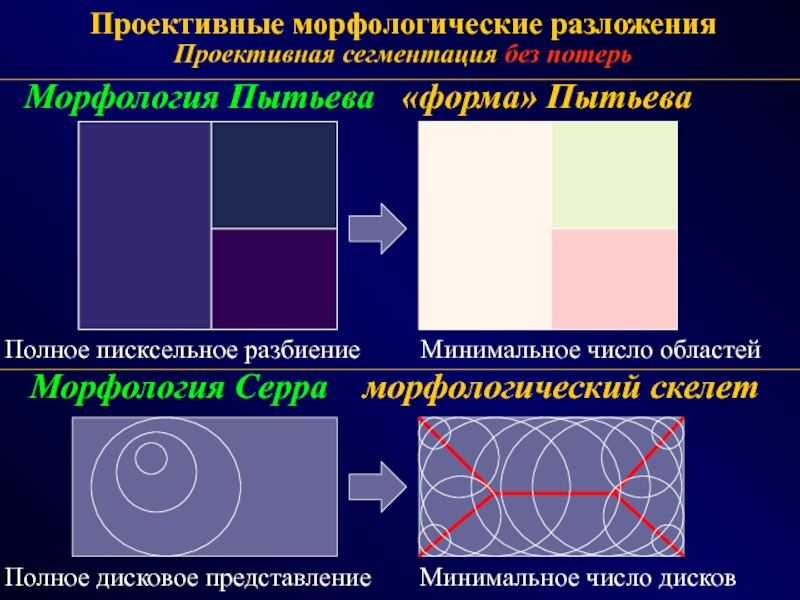
- 54. Проективные морфологические разложения Проективная сегментация без потерь
- 55. Достаточные условия построения проективных операторовФ(A,B)= J(A,B) + α×Q(B)Критериальные проективные морфологии Проективная сегментация с потерями
- 56. Алгоритмические аспекты морфологической сегментации
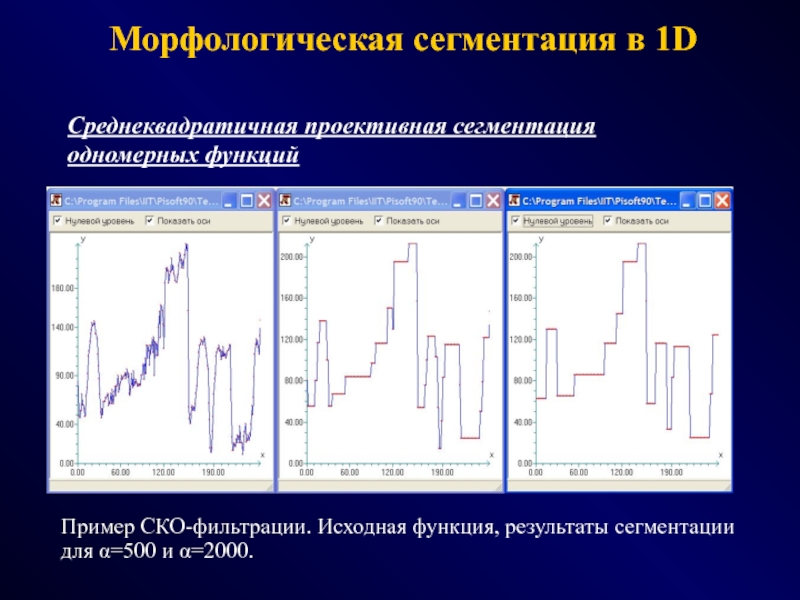
- 57. Среднеквадратичная проективная сегментация одномерных функцийПример СКО-фильтрации. Исходная
- 58. Монотонная проективная фильтрация одномерных функцийПримеры применения операторов
- 59. Монотонная проективная сегментация одномерных функцийПримеры применения операторов
- 60. α=700α=600α=500α=400α=300α=200α=100α=0Монотонная фильтрация и сегментация двумерных кривых (контуров
- 61. α=600α=500α=400α=0α=100α=200α=300α=700Монотонная фильтрация и сегментация двумерных кривых (контуров
- 62. α=1000α=900α=800α=600α=400α=200α=0Морфология на базе оптимальной кусочно-линейной интерполяции двумерных
- 63. Морфологическая сегментация в 2DВарианты по J(A,B)Варианты по
- 64. Морфологическая сегментация в 2D D. Greig, B.
- 65. Пример решения задачи (L1-открытие + N) по
- 66. Представление данных 2 (яркостно-геометрическое)Срезы и сегменты:
- 67. Пример 2D-открытия типа (L1+N)Исходное изображение1395 срезовых сегмента120 сегментов34 сегментов686 сегментов3 сегмента
- 68. Пример 2D-открытия типа (L1+N)Исходное изображение2859 срезовых сегмента111 сегментов18 сегментов545 сегментов2 сегмента
- 69. Пример 2D-открытия типа (L1+N)Исходное изображение3352 срезовых сегмента167 сегментов35 сегментов
- 70. Пример 2D-открытия типа (L1+N)Исходное изображение2358 срезовых сегмента88 сегментов21 сегмент
- 71. Пример 2D-закрытия типа (L1+N)Исходное изображение1584 срезовых сегмента480 сегментов38 сегментов938 сегментов2 сегмента
- 72. Пример 2D-закрытия типа (L1+N)Исходное изображение2527 срезовых сегмента95 сегментов18 сегментов513 сегментов2 сегмента
- 73. Пример 2D-закрытия типа (L1+N)Исходное изображение3542 срезовых сегмента202 сегмента46 сегментов
- 74. Пример 2D-закрытия типа (L1+N)Исходное изображение2527 срезовых сегмента118 сегментов28 сегментов
- 75. Пример 2D-аппроксимации типа (L1+N)Исходное изображение1395 срезовых сегмента102 сегмента23 сегмента326 сегментов2 сегмента
- 76. Пример 2D-аппроксимации типа (L1+N)Исходное изображение2859 срезовых сегмента94 сегментов14 сегментов421 сегментов2 сегмента
- 77. Пример 2D-аппроксимации типа (L1+N)Исходное изображение3542 срезовых сегмента141 сегмент29 сегментов
- 78. Пример 2D-аппроксимации типа (L1+N)Исходное изображение2527 срезовых сегмента74 сегмента14 сегментов
- 79. Пример 2D- аппроксимации типа (L1+TV)Исходное изображение1584 срезовых сегмента123 сегмента45 сегментов666 сегментов21 сегмент
- 80. Пример 2D- аппроксимации типа (L1+TV)Исходное изображение2859 срезовых сегмента257 сегментов209 сегментов700 сегментов106 сегмента
- 81. Пример 2D- аппроксимации типа (L1+TV)Исходное изображение3542 срезовых сегмента871 сегмент159 сегментов
- 82. Пример 2D- аппроксимации типа (L1+TV)Исходное изображение2527 срезовых сегмента351 сегмент204 сегмента
- 83. EVIDENCE-BASED IMAGE ANALYSIS
- 84. Основной современный подход к задаче обнаружения и
- 85. Морфологический анализ свидетельств Вероятностная интерпретация методов морфологического
- 86. Морфологический анализ свидетельств Анализ морфологических свидетельствМорфологическое событие:e(p)={f(A,p)=e∈X}.Морфологическая
- 87. Морфологический анализ свидетельств Анализ морфологических свидетельствПод анализом
- 88. РАЗРАБОТКА ВЫЧИСЛИТЕЛЬНО ЭФФЕКТИВНЫХ АЛГОРИТМОВ АНАЛИЗА МОРФОЛОГИЧЕСКИХ СВИДЕТЕЛЬСТВ
- 89. Способы повышения вычислительной эффективности: • независимое аккумулирование свидетельств
- 90. Последовательность шагов разработки алгоритмаобнаружения и идентификации объектов1. описать
- 91. Пример 1. Метод обнаружения штриховых кодов и текстовых областей на изображениях
- 92. Пример 1. Метод обнаружения штриховых кодов и
- 93. Идея модифицированного преобразования ХафаМетод выделения штриховых и
- 94. Пример 2. Car Collision Avoidance System (CCAS)Road
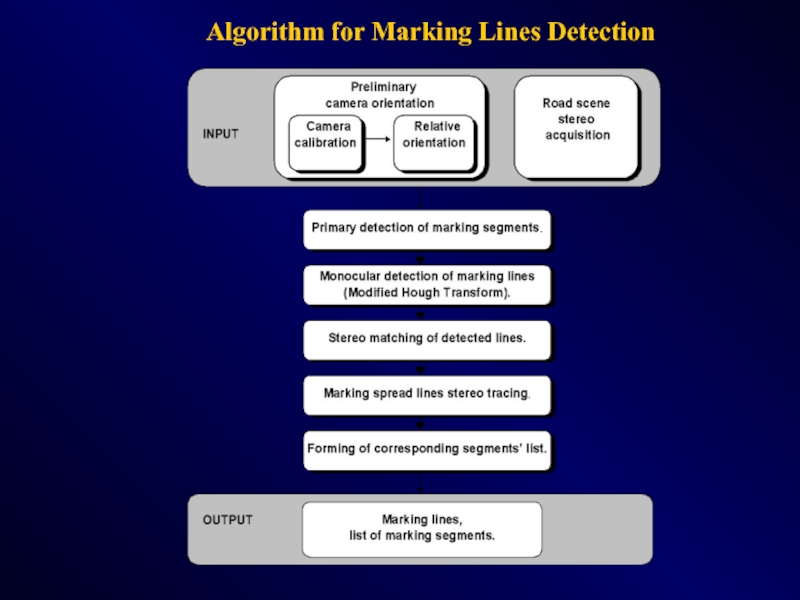
- 95. Algorithm for Marking Lines Detection
- 96. Basic Idea of Marking Lines Detection. Modified
- 97. Marking Lines Detection. Stereo Tracing Stage.Zones of stereo tracing of marking lines are shown.
- 98. Method for 3D object detection based on
- 99. Test field containing 8-12 reference points2-5 stereo
- 100. Extraction of road surface modelDetection of marking
- 101. Example: The coverExample: The pedestrian Distance estimation
- 102. АВТОМАТИЗИРОВАННОЕ КОНСТРУИРОВАНИЕ АЛГОРИТМОВ МОРФОЛОГИЧЕСКОГО АНАЛИЗА СВИДЕТЕЛЬСТВ
- 103. Автоматизированное конструирование алгоритмов обнаружения объектов Постановка задачи
- 104. Автоматизированное конструирование алгоритмов обнаружения объектов1. Метод автоматизированного
- 105. Автоматизированное конструирование алгоритмов обнаружения объектов Конструирование
- 106. Метод преобразования модельных описанийМодель объекта: Преобразования моделей:перестановка
- 107. Пример преобразования модельных описанийМодели: Штриховая линия =
- 108. Алгоритм применения построенной модели процедуры голосования:1. Осуществить
- 109. Проективные морфологии на базе неоднородных структурных
- 110. Принцип конструирования процедуры идентификацииМножество процедур обнаружения:
- 111. Задача условной оптимизации:
- 112. Схема применения генетического алгоритма:1. Ген = одна
- 113. Схема применения генетического алгоритма для формирования морфологических
- 114. Интерпретация результата:1. Процедурная интерпретация = Близкая к
- 115. Conclusions Two generic frameworks for image analysis
- 116. Thank you for attention!
- 117. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Development of Applied Computer Vision Systems Using Projective Morphologies and
Evidence-Based Image Analysis
Systems” (GosNIIAS)Слайд 2FGUP “State Research Institute of Aviation Systems” (GosNIIAS)
Leading Russian organization
in the field of avionics for flight vehicles of civil
and military aviation founded in 194626 Doctors of Sciences, 232 Candidates of Sciences
Educational faculties of MFTI, MAI, MIREA
“Technical Vision” laboratories:
Computer and Machine Vision Laboratory
Laboratory for Close-range Digital Photogrammetry
Laboratory for Long-range Digital Photogrammetry
Laboratory for Optic and Electronic Systems
About 60 developers (engineers and software engineers)
4 Doctors of Science, 8 Candidates of Sciences
More than 300 scientific publications in related area
More information about commercial products and projects:
www.iitvision.ru
JSC “Institute of Information Technologies”:
www.gosniias.ru
Слайд 5Two Vision Frameworks Presented
Vision Framework is a regular scheme for
design of vision algorithms. It’s a special way for thinking
about images and tasks.Projective Morphology scheme is developed based on Serra’s Mathematical Morphology, Pavel’s Shape Theory and Pytiev’s Morphological Analysis. This morphological framework utilizes the structural image modeling with regularization constrains and decides some image segmentation and image comparison problems.
Evidence-Based Image Analysis scheme evolves the voting techniques proposed by Hough, Ballard and Davies. Ii is a voting scheme with the use of simple low-level image events, high- or mid-level parameterized object hypotheses and reasonably sophisticated analysis of voting results. It provides the creation of robust and computationally effective model-based object detection procedures.
Слайд 7MM 1. Математическая морфология Серра Обработка с учетом формы, выделение
деталей
MIN
эрозия
MAX
дилатация
MIN
эрозия
MAX
дилатация
реконструкция A
A
Serra J. Image Analysis and Mathematical
Morphology. Academic Press. London, 1982.Слайд 8MM 1. Математическая морфология Серра
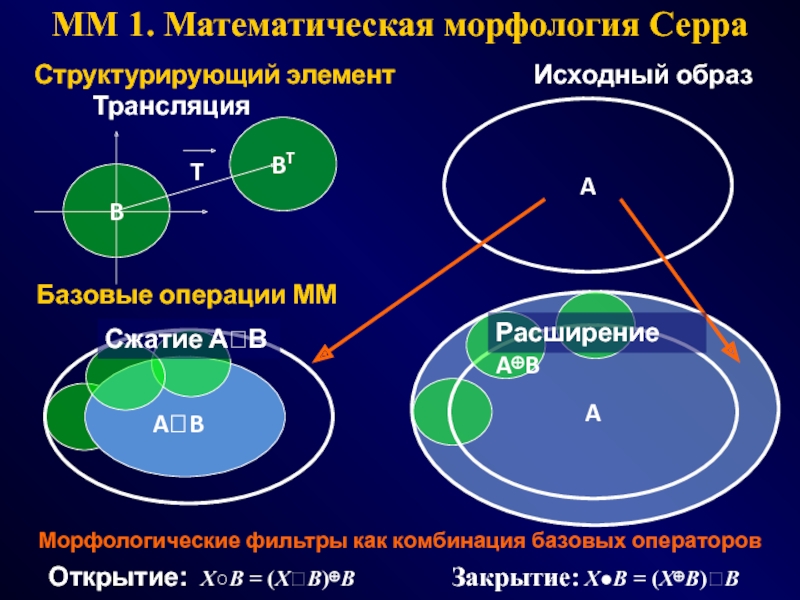
Структурирующий элемент
Исходный образ
B
A
BT
T
Трансляция
A
A
AB
Открытие: X○B = (XB)⊕B
Закрытие: X●B = (X⊕B)B
Сжатие AB
Расширение A⊕B
Базовые операции ММ
Морфологические фильтры как комбинация базовых операторов
Слайд 9MM 1. Математическая морфология Серра
B
BT
T
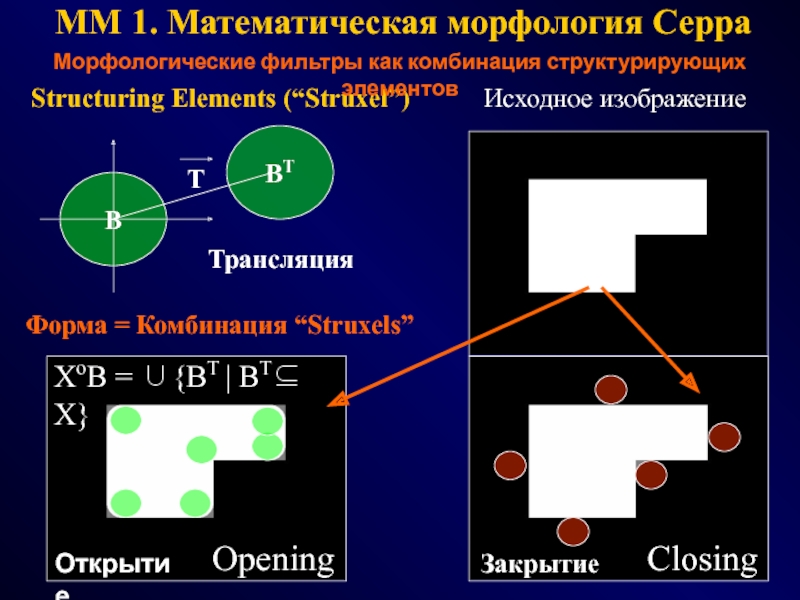
Structuring Elements (“Struxel”)
Исходное изображение
Трансляция
Opening
Closing
XoB = ∪{BT | BT⊆ X}
Форма = Комбинация “Struxels”
Морфологические фильтры как комбинация структурирующих элементов
Открытие
Закрытие
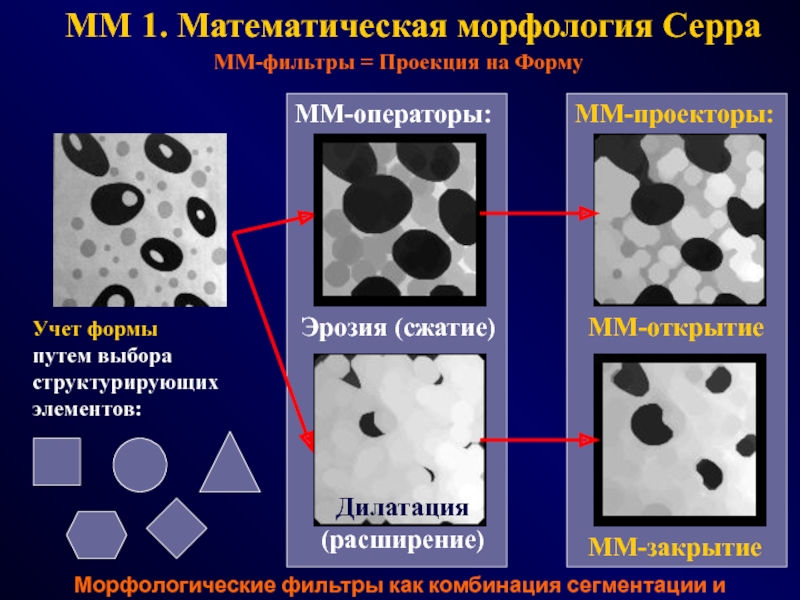
Слайд 10
MM 1. Математическая морфология Серра
ММ-операторы:
ММ-проекторы:
Эрозия (сжатие)
Дилатация
(расширение)
ММ-открытие
ММ-закрытие
ММ-фильтры = Проекция на Форму
Учет формы
путем выбора структурирующих
элементов:
Морфологические фильтры как комбинация сегментации и
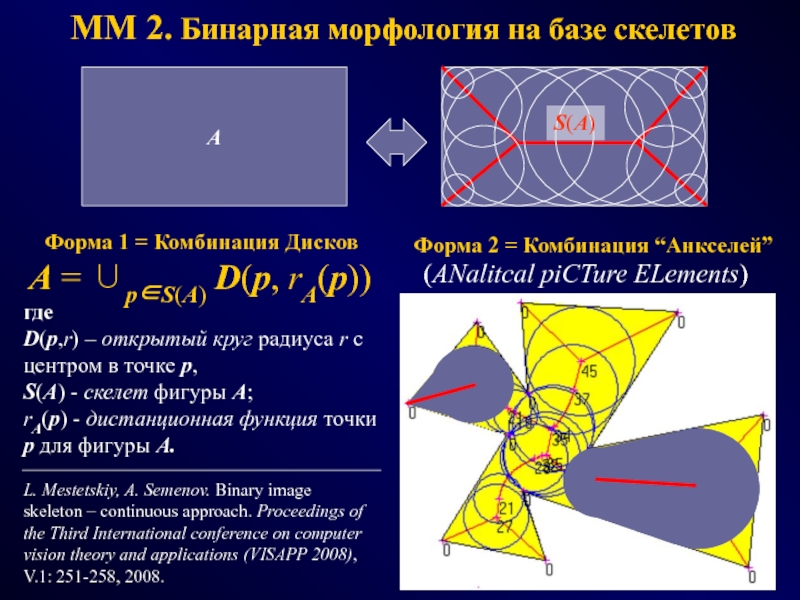
реконструкцииСлайд 11MM 2. Бинарная морфология на базе скелетов
A
Форма 1 =
Комбинация Дисков
A = ∪p∈S(A) D(p, rA(p))
где
D(p,r) –
открытый круг радиуса r с центром в точке p,S(A) - cкелет фигуры A;
rA(p) - дистанционная функция точки p для фигуры A.
S(A)
Форма 2 = Комбинация “Aнкселей”
(ANalitcal piCTure ELements)
L. Mestetskiy, A. Semenov. Binary image skeleton – continuous approach. Proceedings of the Third International conference on computer vision theory and applications (VISAPP 2008), V.1: 251-258, 2008.
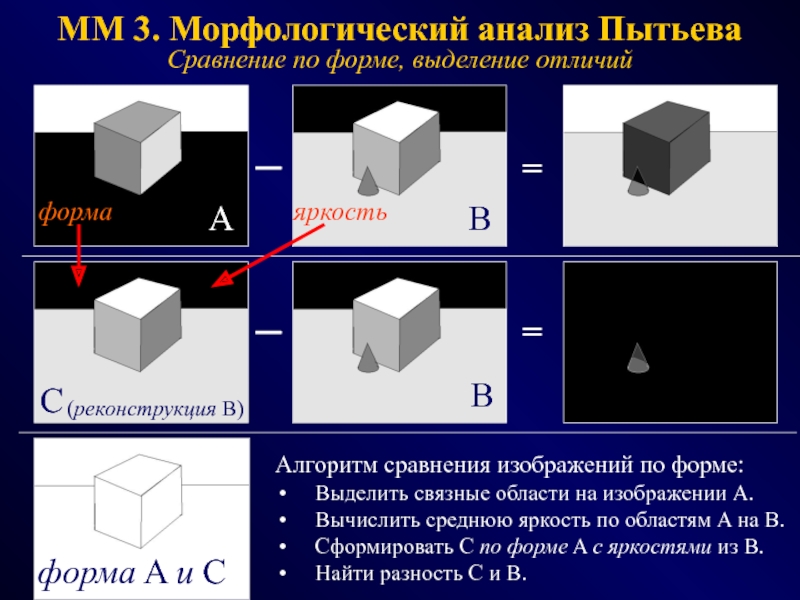
Слайд 12MM 3. Морфологический анализ Пытьева
Сравнение по форме, выделение отличий
─
=
─
=
Алгоритм
сравнения изображений по форме:
Выделить связные области на изображении A.
Вычислить среднюю
яркость по областям A на B.Сформировать C по форме A с яркостями из B.
Найти разность С и B.
A
B
B
C
форма A и С
форма
яркость
(реконструкция B)
Слайд 13
MM 3. Морфологический анализ Пытьева
A1
A2
A3
A4
Индикаторная функция множества Ai
Значение яркости(интенсивности)
пикселя с координатами (x, y) (функция изображения)
с1,…, с4 – яркости
областей A1,…, A4 фона
и граней кубаX
X – поле зрения
Форма = Комбинация элементов-областей
Yu. Pyt’ev. Morphological Image Analysis. Pattern Recognition and Image Analysis. V.3. No1: 19-28, 1993.
Слайд 14
MM 3. Морфологический анализ Пытьева
Изображение , определенное на поле
Х
Форма изображения V(f) в виде множества
- интеграл яркостей по области
AiПроекция вектора g
на плоскость V(f)
Определение коэффициентов ci*
Дифференцируя по ci, получим решение задачи в виде
- площадь области Ai
Проекция на Форму
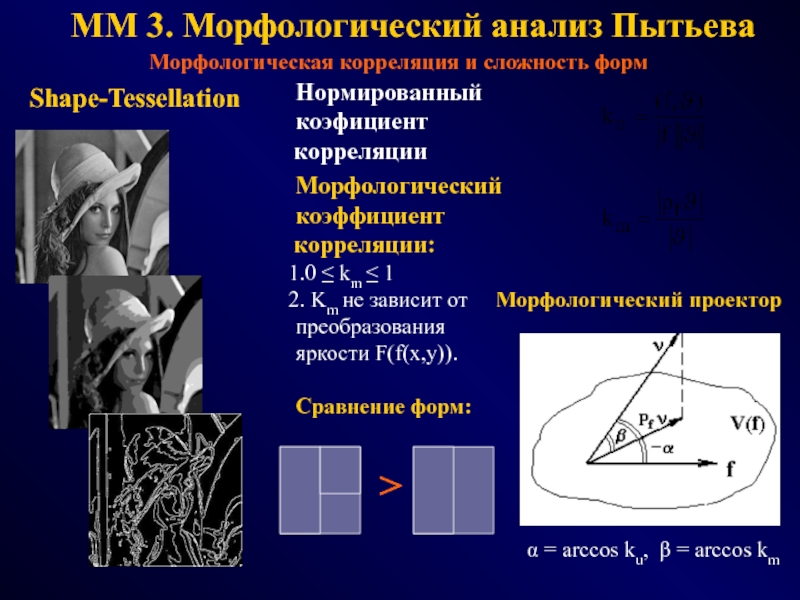
Слайд 15MM 3. Морфологический анализ Пытьева
α = arccos ku, β
= arccos km
Нормированный
коэфициент
корреляции
Морфологический
коэффициент
корреляции:
0 ≤ km ≤ 1
Km не зависит
от Морфологический проектор
преобразования
яркости F(f(x,y)).Сравнение форм:
>
Shape-Tessellation
Морфологическая корреляция и сложность форм
Слайд 16Projective Morphology as a Union of Morphologies
Image Algebra
with Projectors
- Projection to the Shape
- Projection = Segmentation +
Reconstruction- Shape Model = Combination of Shape Elements
Morphological Complexity of Shape Models
Shape Model Fitting by “Precision vs. Complexity” Criterion
Filtering: Projection to the Shape
Segmentation: Regularization of Shape Model
Matching: Morphological Shape Correlation
Extraction: Morphological Background Normalization (Hit-Miss-Transform)
Detection: Morphological Evidence Analysis
Features: Morphological Decomposition
Morphological Spectrum
Morphological Skeleton
Common Instruments
Common Aspects
Слайд 18Проекторы как распознающие операторы
(М. Павель)
Морфологический фильтр: преобразование изображения
к виду,
соответствующему заданному классу форм.
Алгебраический проектор:
F(X)=F(F(X))
Геометрическая интерпретация:
Два способа описания класса:
Проектор –
оператор, ставящий в соответствие любому образу образ из модельного множества.Модель (модельное множество) – множество стабильных элементов проектора.
M. Pavel, Fundamentals of Pattern Recognition. Marcel Dekker. Inc, New York, 1989.
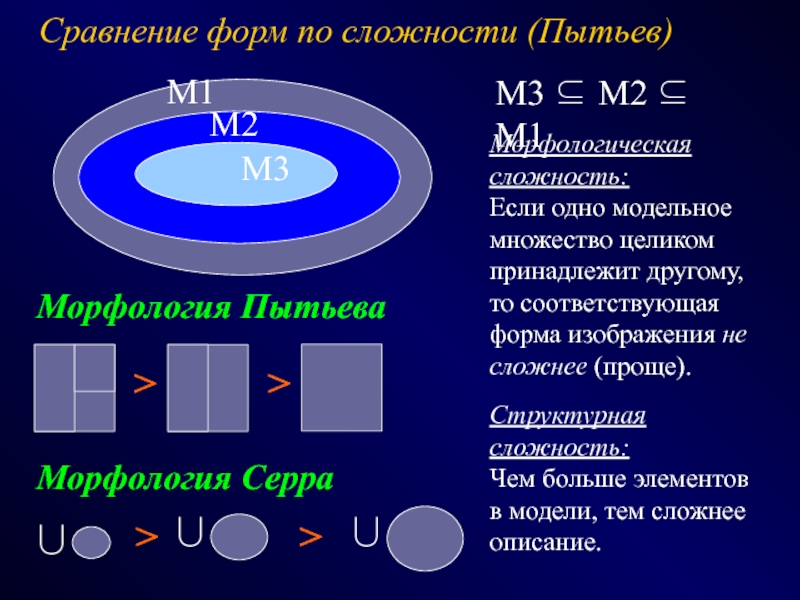
Слайд 19Сравнение форм по сложности (Пытьев)
M1
M2
M3
M3 ⊆ M2 ⊆ M1
Морфологическая
сложность:
Если одно модельное множество целиком принадлежит другому,
то соответствующая форма
изображения не сложнее (проще). >
>
Морфология Пытьева
Морфология Серра
∪
>
>
∪
∪
Структурная сложность:
Чем больше элементов в модели, тем сложнее описание.
Слайд 20
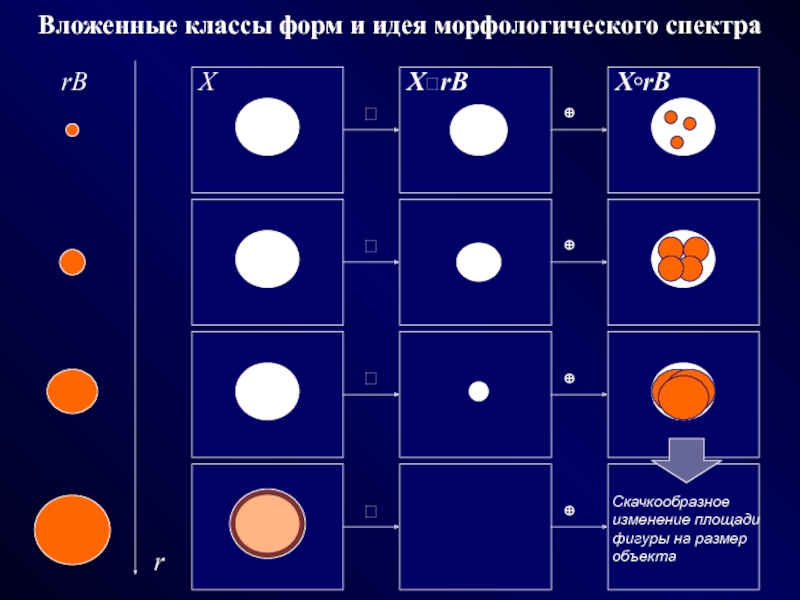
Вложенные классы форм и идея морфологического спектра
⊕
⊕
⊕
⊕
r
Скачкообразное изменение площади фигуры
на размер объекта
X
rB
X◦rB
XrB
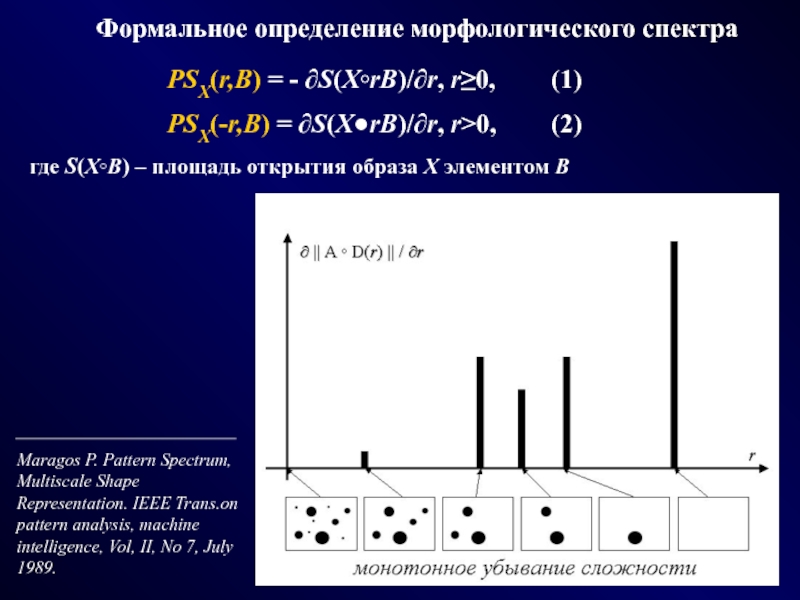
Слайд 21PSX(r,B) = - ∂S(X◦rB)/∂r, r≥0, (1)
PSX(-r,B) = ∂S(X●rB)/∂r, r>0, (2)
где
S(X◦B) – площадь открытия образа Х элементом B
Формальное определение морфологического
спектраMaragos P. Pattern Spectrum, Multiscale Shape Representation. IEEE Trans.on pattern analysis, machine intelligence, Vol, II, No 7, July 1989.
Слайд 22
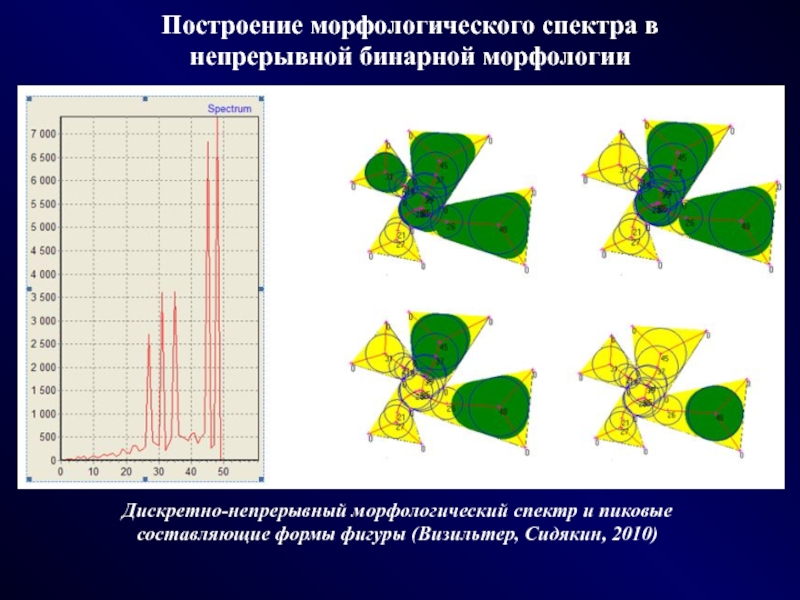
Построение морфологического спектра в непрерывной бинарной морфологии
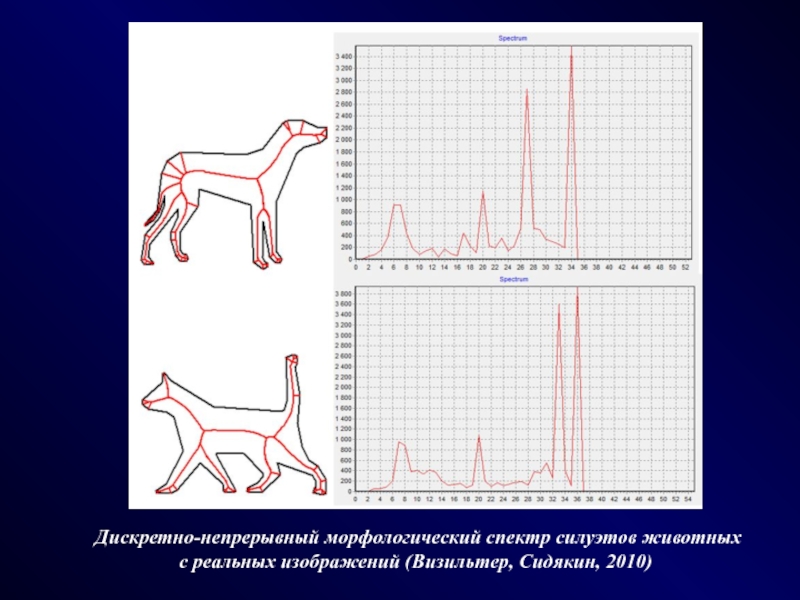
Дискретно-непрерывный морфологический спектр
и пиковые составляющие формы фигуры (Визильтер, Сидякин, 2010)
Слайд 23Дискретно-непрерывный морфологический спектр силуэтов животных с реальных изображений (Визильтер, Сидякин,
2010)
Слайд 24СЕГМЕНТАЦИЯ + РЕКОНСТРУКЦИЯ (поиск нетривиальных описаний и построение морфологических систем из готовых
«кубиков»)
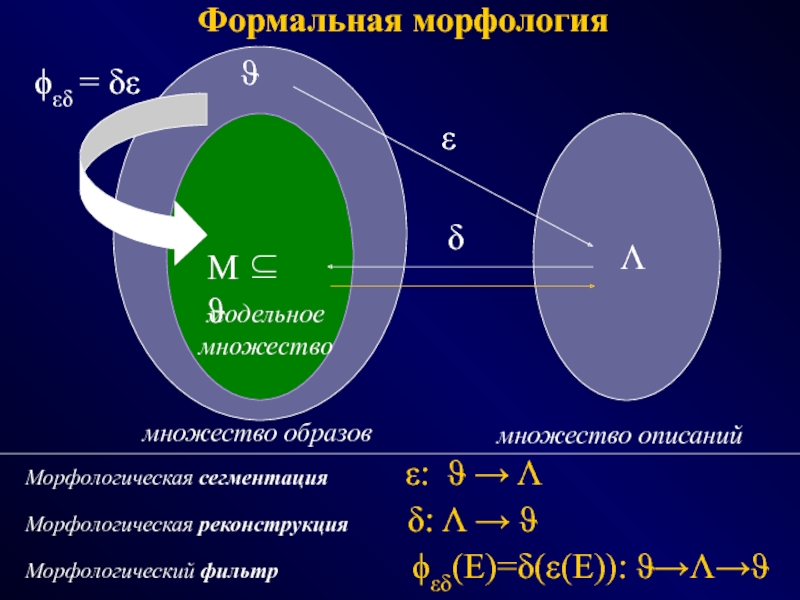
Слайд 25Формальная морфология
ϑ
Λ
M ⊆ ϑ
ε
δ
ϕεδ = δε
множество образов
множество описаний
модельное
множество
Морфологическая сегментация
ε: ϑ → Λ
Морфологическая реконструкция
δ: Λ → ϑМорфологический фильтр ϕεδ(E)=δ(ε(E)): ϑ→Λ→ϑ
Слайд 26Сегментация + Реконструкция
множество образов
множество описаний
Искусственный
изоморфизм
Естественный
гомоморфизм
568=5×102+6×101+8×10
40=1×25+1×23
28=22 ×
71
f(x)
a4 x4+a3 x3+a2 x2+a1 x+a0
Естественный
изоморфизм
Позиционные системы счисления
Разложение на простые
множителиАппроксимация полиномами
Слайд 27Способ описания формы:
Преобразование Хафа (HT)
Голосование точек в аккумулятор
Анализ аккумулятора
Параметризация:
НТ
Пространство
параметров
Hough P.V.C.
Methods, Means for Recognizing Complex Patterns. − U.S., Patent 3069654,
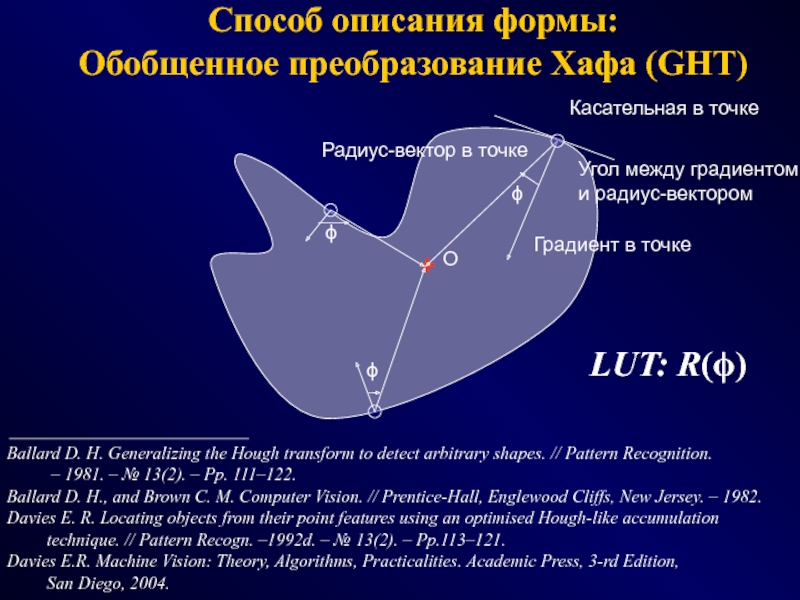
1962.Слайд 28Способ описания формы:
Обобщенное преобразование Хафа (GHT)
+
О
Касательная в точке
Градиент в
точке
Радиус-вектор в точке
Угол между градиентом
и радиус-вектором
ϕ
ϕ
ϕ
LUT: R(ϕ)
Ballard D. H. Generalizing
the Hough transform to detect arbitrary shapes. // Pattern Recognition.
– 1981. – № 13(2). – Pp. 111–122.Ballard D. H., and Brown C. M. Computer Vision. // Prentice-Hall, Englewood Cliffs, New Jersey. – 1982.
Davies E. R. Locating objects from their point features using an optimised Hough-like accumulation technique. // Pattern Recogn. –1992d. – № 13(2). – Pp.113–121.
Davies E.R. Machine Vision: Theory, Algorithms, Practicalities. Academic Press, 3-rd Edition, San Diego, 2004.
Слайд 29Морфологии Серра на базе
преобразования Хафа и GHT
H-открытие - объединение проекций
изображения A(p) на отдельные прямые линии:
Pr(A(p),t) = MAXq∈Q(A(q,t)∙Pr(A(p),ϕ(p,q))) = MAXq∈Q(A(q,t)∙A(p)∙ϕ(p,q)),
где
p=(x,y); q=(ρ,θ) – параметры нормальной параметризации прямой; Q – пространство параметров; ϕ(p,q)∈{0,1} – характеристическая функция прямой с параметрами q; A(q,t)∈{0,1} – аккумулятор преобразования Хафа, бинаризованный по порогу t. (а) (b) (с)
Пример морфологического H-открытия: a – исходное бинарное изображение;
b – аккумулятор пространства Хафа c – результат H-открытия.
На исходном контурном препарате выделены глобальные прямолинейные структуры.
Аналогичным образом строится монотонная проективная морфология на базе
обобщенного преобразования Хафа (GHT).
Слайд 33Морфологии из «готовых кубиков»
Идея: Построение различных модульных морфологических операторов
путем комбинирования разных операторов сегментации с разными операторами реконструкции.
Пример: селективные
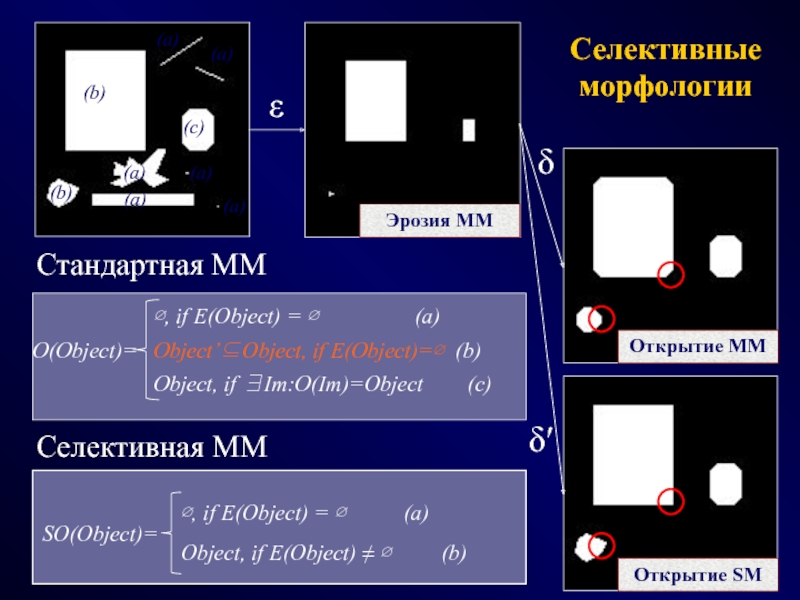
морфологии на базе операторов ММ СерраСлайд 34Селективные морфологии
(a)
(b)
(c)
(a)
(b)
(a)
(a)
Открытие MM
(a)
(a)
O(Object)=
∅, if E(Object) = ∅
(a)
Object’⊆Object, if E(Object)=∅ (b)
Object, if ∃Im:O(Im)=Object
(c) ∅, if E(Object) = ∅ (a)
Object, if E(Object) ≠ ∅ (b)
SO(Object)=
Стандартная ММ
Селективная ММ
Открытие SM
Эрозия MM
ε
δ
δ′
Слайд 43Селективные морфологии
Im
E1D(Im)
SO1D(Im)
Im-SO1D(Im)
Контурная селективная морфология
(на базе оператора удаления заданного числа концевых
точек)
Слайд 45Морфологические алгебры
1, если B⊆A
r(A,B) =
0, если B⊄APr(A,B)=∅
Например, для ММ Серра
B
A
Pr(A,B)=B
B
A
Projective space of patterns (images) is an algebraic system <Ψ, Ω, ∙, V, μ, Pr, E>,
where Ψ is a set of scalars including 0 and 1; Ω is the set of patterns with “zero pattern” ∅; ‘∙’ is the multiplicative group operation of multiplication of scalars
Ψ × Ψ → Ψ and a scalar by pattern multiplication Ψ × Ω → Ω;
‘V’ ∈ {‘+’, ‘×’, ‘∪’, ‘∩’, ‘∨’, ‘∧’, ‘min’, ‘max’, …} is the additive Abel semi-group of scalars fusion Ψ × Ψ → Ψ and patterns fusion Ω×Ω→Ω; μ is the norm of the pattern
Ω → R (μ(A) = ||A||, ||∅|| = 0); set of basic patterns (primitives) E = {E1, …, En} is the basis of the morphological pattern decomposition.
Let E will denote the corresponding morphological subspace E ⊆ Ω generated by the algebraic closing of basis E relative to‘∙,V’-combination. The operator of linear projection of pattern onto the pattern has a form
Pr(A,B) = r(A,B)∙B: Ω → B ⊆ Ω,
where r(A,B) ∈ Ψ is the coefficient of linear connection of A relative to pattern B.
Слайд 46Проективные морфологические разложения
Проективные морфологические разложения
Использование морфологических разложений образов в качестве
признаковых описаний этих образов является обоснованным.
Отсюда и все полезные
практические свойства таких разложений.Слайд 47Проективные морфологические разложения
Типы морфологических разложений
Условие разложимости:
∃ E⊆Ω: Pr(A,E) = Vk=1..n(Pr(A,Ek))
= Vk=1..n(r(A,Ek)∙Ek)
Слайд 48Проективные морфологические разложения
Ортогональные морфологии на базе БПФ и т.п.
БПФ, ДКП,
фильтры НЧ, ВЧ
Вейвлет-преобразование и фильтры
Слайд 49Проективные морфологические разложения
Морфологический анализ изображений
Переход от образов к изображениям
(двумерным функциям):
Введем пространства параметров изображения P и разложения Q:
A→A(p); Ek→Ek(p)→ϕ(p,q);
E→E(p,q).Морфологические разложения изображений:
Морфо-геометрическая проекция:
Pr(A(p),E(p,q))=Vq∈Q(A(q)∙ϕ(p,q)).
Морфо-геометрическое разложение:
dec(A(p))=A(q): Ω(P)→Θ(Q).
Проекция разложения на разложение:
Pr(A(q),B(q))=r(A(p),B(p))∙B(q).
Нормированный коэффициент линейной корреляции разложений:
K(A(q),B(q)) = ||Pr(A(q),B(q))||/||A(q)||.
Слайд 50Проективные морфологические разложения
Морфологический анализ изображений
Фильтрация изображений с использованием разложений:
Слайд 51Проективные морфологические разложения
Морфологический анализ изображений
Структурное сравнение изображений (обобщение методики
Ю.П. Пытьева)
Структурный проектор = Морфологический фильтр, применяемый к образу A,
область пропускания которого согласована с образом B.Характеристический базис образа B:
Eχ(B)={χ(bk)∙Ek, Ek∈E},
χ(x)={0, если x=0; 1 – в противном случае}, где E –исходный базис, χ(x) - индикатор структурной связи.
Морфологическая проекция образа A на модель образа [B]:
Pr(A,[B]) = Vk=1..n(ak∙χ(bk)∙Ek) = Pr(A,Eχ(B)).
Морфологическая проекция разложений:
Pr(a,[b]) = Pr({ak},[{bk}]) = {ak∙χ(bk)}.
Структурный морфологический коэффициент корреляции:
Kстр(A,B)= ||Pr(a,[b])|| / ||a||, где A,B∈Ω; a=dec(A),b=dec(B)∈Θ, со стандартными свойствами:
(a) 0 ≤ Kстр(A,B) ≤ 1; (b) Kстр(A,A) = 1; (c) Kстр(A,B) = 0 ⇔ Pr(A,[B]) = ∅.
Класс морфологически эквивалентных структур:
В={X∈Ω: Kстр(X,B)=1}.
Отношение «более простой/более сложный по структуре»:
(Kстр(A,B) = 1, Kстр(B,A) < 1) ⇔ («A сложнее B», «B проще A»).
Слайд 52Проективные морфологические разложения
Конструирование алгоритмов обнаружения объектов
Обнаружение объектов с использованием
разложений:
Слайд 53
Проективные морфологические разложения
Морфологические операторы сегментации и сжатия данных
Морфологическая сегментация
на базе проективных разложений
Слайд 54
Проективные морфологические разложения
Проективная сегментация без потерь
Морфология Пытьева «форма»
Пытьева
Морфология Серра морфологический скелет
Минимальное число областей
Минимальное число дисков
Полное писксельное
разбиениеПолное дисковое представление
Слайд 55Достаточные условия построения проективных операторов
Ф(A,B)= J(A,B) + α×Q(B)
Критериальные проективные морфологии
Проективная
сегментация с потерями
Слайд 57Среднеквадратичная проективная сегментация
одномерных функций
Пример СКО-фильтрации. Исходная функция, результаты сегментации
для α=500
и α=2000.
Морфологическая сегментация в 1D
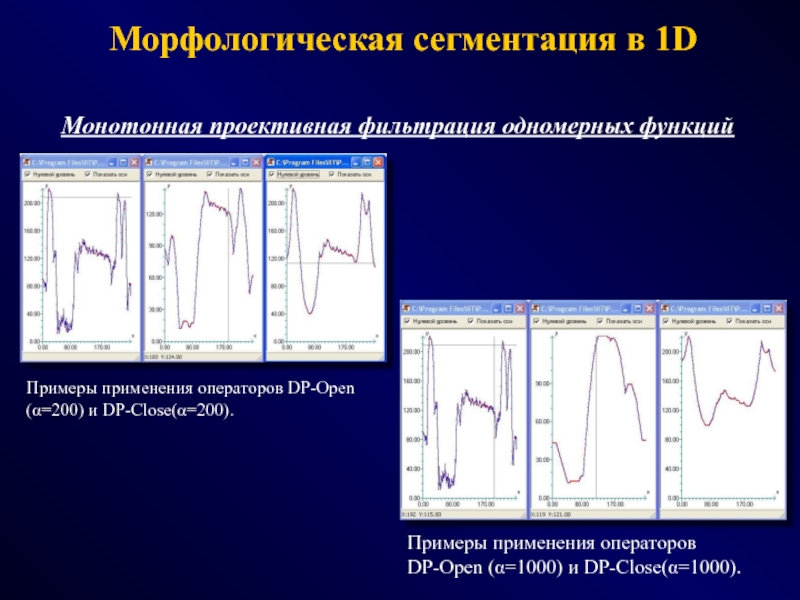
Слайд 58Монотонная проективная фильтрация одномерных функций
Примеры применения операторов DP-Open (α=200) и
DP-Close(α=200).
Примеры применения операторов DP-Open (α=1000) и DP-Close(α=1000).
Морфологическая сегментация в 1D
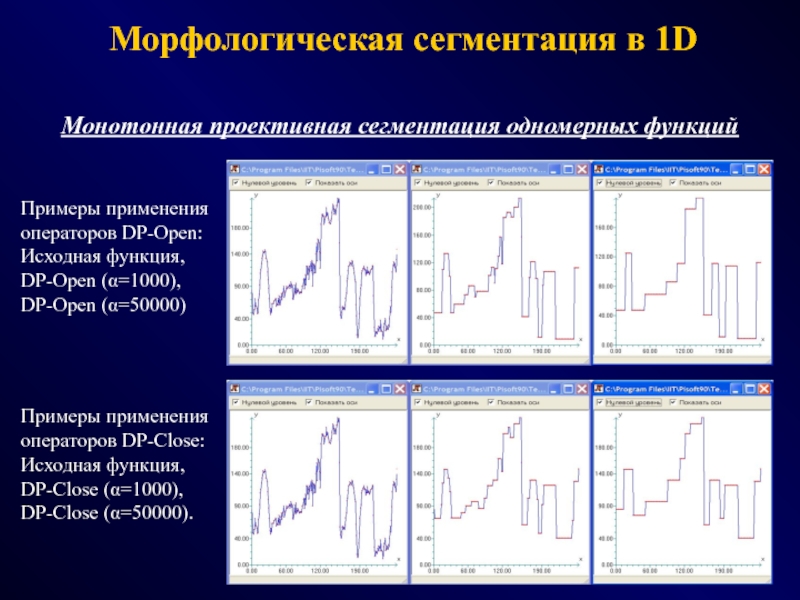
Слайд 59Монотонная проективная сегментация одномерных функций
Примеры применения операторов DP-Open: Исходная функция,
DP-Open (α=1000), DP-Open (α=50000)
Примеры применения операторов DP-Close: Исходная функция, DP-Close
(α=1000), DP-Close (α=50000). Морфологическая сегментация в 1D
Слайд 60
α=700
α=600
α=500
α=400
α=300
α=200
α=100
α=0
Монотонная фильтрация и сегментация двумерных кривых (контуров бинарных изображений)
Пример
кусочно-линейной сегментации типа «закрытие».
Морфологическая сегментация в 1,5D
Слайд 61
α=600
α=500
α=400
α=0
α=100
α=200
α=300
α=700
Монотонная фильтрация и сегментация двумерных кривых (контуров бинарных изображений)
Пример
кусочно-линейной сегментации типа «открытие».
Морфологическая сегментация в 1,5D
Слайд 62
α=1000
α=900
α=800
α=600
α=400
α=200
α=0
Морфология на базе оптимальной кусочно-линейной интерполяции двумерных кривых (контуров бинарных
изображений)
Морфологическая сегментация в 1,5D
Ф(f,L) = -J(L) + α×Q(L) →
min(L),
где J(L) – длина графика ломаной; Q(L) – число узловых точек.Слайд 63
Морфологическая сегментация в 2D
Варианты по J(A,B)
Варианты по Q(εB)
L1-аппроксимация: |A-B|
СКО-аппроксимация:
|A-B|2
L1-открытие: |A-B|, B≤A
L1-закрытие: |A-B|, A≤B
N –
число элементов описанияTV - Суммарная длина контуров
D - Размер дескриптора
…
Q
J
Конкретный тип задачи
Слайд 64Морфологическая сегментация в 2D
D. Greig, B. Porteous, A. Seheult.
Exact maximum a posteriori estimation for binary images // Journal
of the Royal Statistical Society 1989. Vol. 51, No. 2 Pp. 271279.Y. Boykov, V. Kolmogorov. Computing geodesics and minimal surfaces via graph cuts // In Proc. IEEE International Conf. Computer Vision (ICCV) 2003. Pp. 2633.
Y. Boykov, V. Kolmogorov. An experimental comparison of min-cut/max-ow algorithms for energy minimization in vision // IEEE Trans. Pattern Analysis and Machine Intelligence (PAMI) 2004. Vol. 26, No. 9. Pp. 11241137.
J. Darbon and M. Sigelle. Image Restoration with Discrete Constrained Total Variation Part I: Fast and Exact Optimization // Journal of Mathematical Imaging and Vision (JMIV). Vol 26 n.3, pp. 261-276, December 2006.
J. Darbon and M. Sigelle. Image Restoration with Discrete Constrained Total Variation Part II: Levelable Functions, Convex and Non-Convex Cases // Journal of Mathematical Imaging and Vision (JMIV) Vol 26 n.3, pp. 277-291, December 2006.
Visilter Yu., Gorbatsevich V. Morphological Image Analysis Using Dynamic Programming and Stacked Representations // Vestnik of Computer and Information Technologies, 2011, N3, pp.7-15. (in Russian)
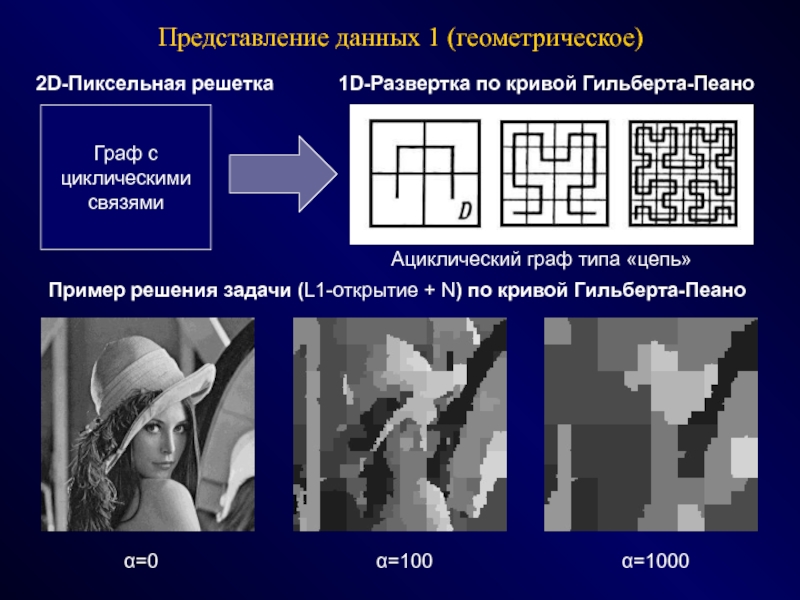
Слайд 65Пример решения задачи (L1-открытие + N) по кривой Гильберта-Пеано
α=0
α=100
α=1000
Представление данных
1 (геометрическое)
Граф с
циклическими
связями
1D-Развертка по кривой Гильберта-Пеано
2D-Пиксельная решетка
Ациклический граф типа «цепь»
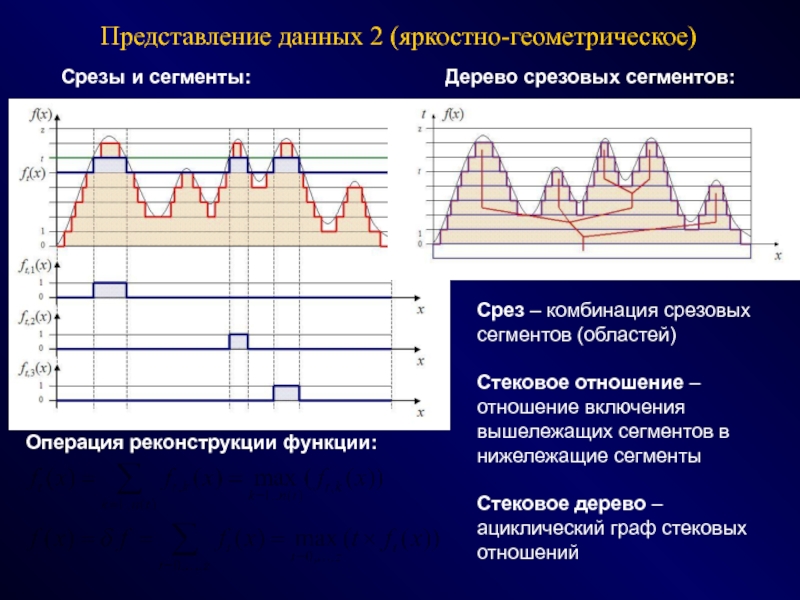
Слайд 66Представление данных 2 (яркостно-геометрическое)
Срезы и сегменты:
Дерево срезовых сегментов:
Срез – комбинация срезовых сегментов (областей)
Стековое отношение – отношение включения вышележащих сегментов в нижележащие сегменты
Стековое дерево – ациклический граф стековых отношений
Операция реконструкции функции:
Слайд 67Пример 2D-открытия типа (L1+N)
Исходное изображение
1395 срезовых сегмента
120 сегментов
34 сегментов
686 сегментов
3
сегмента
Слайд 68Пример 2D-открытия типа (L1+N)
Исходное изображение
2859 срезовых сегмента
111 сегментов
18 сегментов
545 сегментов
2
сегмента
Слайд 69Пример 2D-открытия типа (L1+N)
Исходное изображение
3352 срезовых сегмента
167 сегментов
35 сегментов
Слайд 70Пример 2D-открытия типа (L1+N)
Исходное изображение
2358 срезовых сегмента
88 сегментов
21 сегмент
Слайд 71Пример 2D-закрытия типа (L1+N)
Исходное изображение
1584 срезовых сегмента
480 сегментов
38 сегментов
938 сегментов
2
сегмента
Слайд 72Пример 2D-закрытия типа (L1+N)
Исходное изображение
2527 срезовых сегмента
95 сегментов
18 сегментов
513 сегментов
2
сегмента
Слайд 73Пример 2D-закрытия типа (L1+N)
Исходное изображение
3542 срезовых сегмента
202 сегмента
46 сегментов
Слайд 74Пример 2D-закрытия типа (L1+N)
Исходное изображение
2527 срезовых сегмента
118 сегментов
28 сегментов
Слайд 75Пример 2D-аппроксимации типа (L1+N)
Исходное изображение
1395 срезовых сегмента
102 сегмента
23 сегмента
326 сегментов
2
сегмента
Слайд 76Пример 2D-аппроксимации типа (L1+N)
Исходное изображение
2859 срезовых сегмента
94 сегментов
14 сегментов
421 сегментов
2
сегмента
Слайд 77Пример 2D-аппроксимации типа (L1+N)
Исходное изображение
3542 срезовых сегмента
141 сегмент
29 сегментов
Слайд 78Пример 2D-аппроксимации типа (L1+N)
Исходное изображение
2527 срезовых сегмента
74 сегмента
14 сегментов
Слайд 79Пример 2D- аппроксимации типа (L1+TV)
Исходное изображение
1584 срезовых сегмента
123 сегмента
45 сегментов
666
сегментов
21 сегмент
Слайд 80Пример 2D- аппроксимации типа (L1+TV)
Исходное изображение
2859 срезовых сегмента
257 сегментов
209 сегментов
700
сегментов
106 сегмента
Слайд 81Пример 2D- аппроксимации типа (L1+TV)
Исходное изображение
3542 срезовых сегмента
871 сегмент
159 сегментов
Слайд 82Пример 2D- аппроксимации типа (L1+TV)
Исходное изображение
2527 срезовых сегмента
351 сегмент
204 сегмента
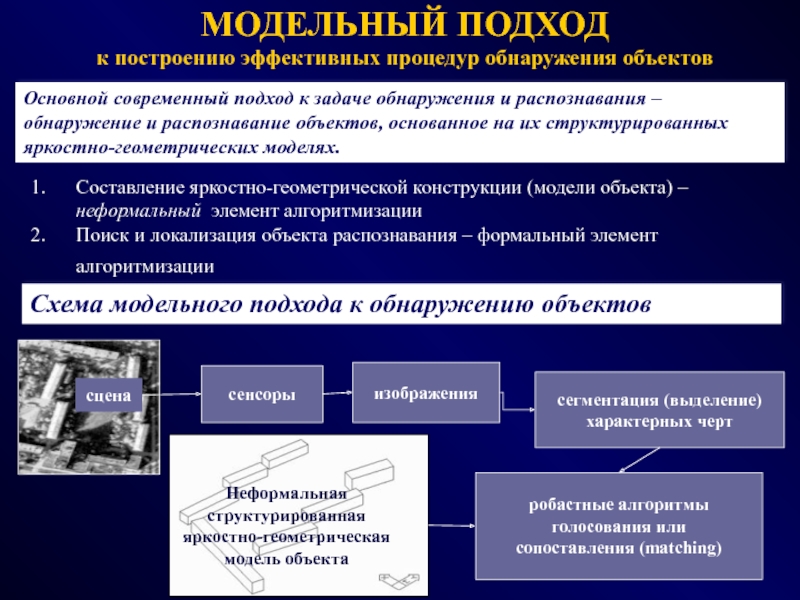
Слайд 84Основной современный подход к задаче обнаружения и распознавания – обнаружение
и распознавание объектов, основанное на их структурированных яркостно-геометрических моделях.
Составление яркостно-геометрической
конструкции (модели объекта) – неформальный элемент алгоритмизацииПоиск и локализация объекта распознавания – формальный элемент алгоритмизации
Схема модельного подхода к обнаружению объектов
робастные алгоритмы
голосования или
сопоставления (matching)
сцена
сенсоры
изображения
сегментация (выделение)
характерных черт
Неформальная
структурированная
яркостно-геометрическая
модель объекта
МОДЕЛЬНЫЙ ПОДХОД
к построению эффективных процедур обнаружения объектов
Слайд 85Морфологический анализ свидетельств
Вероятностная интерпретация методов морфологического анализа изображений
Вероятностная модель формирования
образа
P(M): Ω→[0,1],
Вероятностная модель регистрации изображения
P(L/M): M→[0,1],
Вероятностная модель искажений
P(A/L): M×Ω→[0,1]
Критерий максимальной вероятности
P(A,L)=P(A/L)×P(L/M)×P(M)→max(L).
Оператор максимально вероятной
реконструкции образаψ: Ω→M, ψ(A)=L: P(A,L)→max(L).
Слайд 86Морфологический анализ свидетельств
Анализ морфологических свидетельств
Морфологическое событие:
e(p)={f(A,p)=e∈X}.
Морфологическая гипотеза:
h(q)={ψ(A) = L(q)}.
Модель голосования:
P(E(A),h(q))=Πp∈X,
P(e(p),h(q))→max(h(q)),
где E(A) – совокупность морфологических событий или точнее совокупное морфологическое
событие, связанное с образом A; h(q)⊆H(Θ), H(Θ) – пространство морфологических гипотез; P(e(p),h(q)) - вероятностная модель морфологического голосования.Носитель гипотезы (множество влияющих событий):
S(h(q))={e(p): ∃h′(q)≠h(q): P(e(p),h(q))≠P(e(p),h′(q))}.
Носитель события (множество влияющих гипотез):
S(e(p))={h(q): ∃e′(p)≠e(p): P(e(p),h(q))≠P(e′(p),h(q))}.
Полную группу событий, относящихся к одному признаку f(p), будем называть доменом событий, полную группу гипотез, соответствующую различным значениям L(q) – доменом гипотез.
Слайд 87Морфологический анализ свидетельств
Анализ морфологических свидетельств
Под анализом морфологических свидетельств понимается
следующая процедура:
Морфологические
события подают голоса (свидетельствуют) в пользу морфологических гипотез.
Голоса накапливаются (свидетельства
суммируются)Наиболее вероятной считается та гипотеза, в пользу которой подано максимальное количество голосов (накоплена максимальная сумма свидетельств).
Возможность факторизации функции вероятности является необходимым и достаточным условием возможности независимого (от порядка вычислений) аккумулирования (накопления) свидетельств.
Метод анализа морфологических свидетельств
строится экспертная вероятностная модель, описывающая связь между особенностями изображения (характерными чертами) и гипотезой о принадлежности объекта заданной яркостно-геометрической модели
вероятностная модель используется непосредственно в ходе низкоуровневого анализа изображения
каждая обнаруженная особенность изображения (ХЧ) рассматривается как событие, свидетельствующее в пользу гипотезы (ряда гипотез) о наличии и характеристиках искомого объекта (голосование в специальном аккумуляторном пространстве).
Слайд 89Способы повышения вычислительной эффективности:
• независимое аккумулирование свидетельств
• декомпозиция вектора параметров
S(θ)=S'(θ')∙S"(θ")
• редукция вектора параметров S(θ)→S'(θ')
• загрубление модели объекта M → M'⊇M
• иерархический
анализ свидетельствМодульная схема алгоритма обнаружения
• обработка изображения по схеме голосования с целью выделения объектов или их составляющих
• анализ аккумулятора с целью определения положения и/или ориентации объектов
• повторный анализ изображения с целью проверки природы обнаруженных объектов и уточнения их параметров
Морфологический анализ свидетельств
Слайд 90Последовательность шагов разработки алгоритма
обнаружения и идентификации объектов
1. описать модели объекта, регистрации
и искажений
2. определить степень загрубления модели объекта
3. осуществить
необходимую редукцию параметров4. определить типы «событий»
5. составить качественную вероятностную модель
6. определить процедуру голосования
7. определить соответствующую процедуру анализа аккумулятора
8. разработать процедуру постпроверки достоверности детектирования
Морфологический анализ свидетельств
Слайд 92Пример 1. Метод обнаружения штриховых кодов и текстовых областей на
изображениях
Обнаружение штриховых кодов. Постановка задачи
Модель объекта. Прямоугольная область плоскости, заполненная
белыми и черными полосами. Ширина полос может быть различной.Модель регистрации. Геометрическая - проективные преобразования с малыми углами (≈аффинные). Радиометрическая - отображение черно-белой палитры на шкалу серого цвета (0-15).
Модель искажений. По яркости - блики, перечеркивание, замещение фрагментов. По геометрии - изгибы и "коробление" несущей поверхности.
Обнаружение штриховых кодов. Разработка алгоритма
1. Загрубление модели. Прямоугольная область плоскости (x1,у1, x2,у2, x3,у3, x4,у4) с высокой колинеарностью градиентов.
2. Загрубление и декомпозиция вектора параметров. Модель "четыре угла" преобразуется к модели "четыре прямые" (ρ1,θ,ρ2,θ+90°,ρ3,θ,ρ4,θ+90°). Отсюда декомпозиция модели на кодосодержащую полосу (ρ1,ρ2,θ) и положение в полосе (ρ3, ρ4).
3. Аккумулирование свидетельств. Голоса пикселей с высоким градиентом аккумулируются в двухпараметрическом пространстве Hough (ρ,θ) с учетом направления градиента.
Слайд 93
Идея модифицированного преобразования Хафа
Метод выделения штриховых и текстовых строк в
пространстве Хафа
Исходное изображение и голосование с учетом направления градиента
Область с
выделенными
машиносчитываемыми строкамиСоответствующий аккумулятор пространства Хафа
MHT для обнаружения
штриховых кодов и текстовых строк
1
2
3
4
1
2
3
4
Обрабатывается полутоновое
изображение
2. Объекты поиска – полосы
(группы прямых)
3. Голосуют точки с высоким
модулем градиента яркости
4. Голосование с учетом
направления градиента в точке
5. Анализ аккумулятора – поиск
сигнала заданной формы
Особенности метода
x
y
ϴ
ρ
x
y
ϴ
ρ
Слайд 94Пример 2. Car Collision Avoidance System (CCAS)
Road 3D model reconstruction
based on marking line recognition
Own lane detection, car auto-orientation on
straight and curved roadDetection and tracking of any object, which is not belong to the road surface
Слайд 96Basic Idea of Marking Lines Detection.
Modified Hough Transform.
- Pair-wise voting
of horizontal segments
- Natural parametrisation (xTop,xBottom)
- Bundle of parallel 3D-lines,
those are in a common plane and intersect at one vanishing point on image plane, corresponds to a set of points on one straight line in the accumulator spaceСлайд 97Marking Lines Detection. Stereo Tracing Stage.
Zones of stereo tracing of
marking lines are shown.
Слайд 98Method for 3D object detection
based on differential orthoimage
Detection of 3D
objects on the curved road surface
Recognition of possible situation:
1) Object
is standing
on the surface;2) Object is drawn
on the surface
Слайд 99Test field containing 8-12 reference points
2-5 stereo images acquisition from
various distances
(10-40m)
Determining 2-6 reference distances with high precision
Automated relative orientation
Слайд 100Extraction of road surface model
Detection of marking lines segments using
machine vision procedure
reconstruction of 3D coordinates of road points
Слайд 101Example: The cover
Example: The pedestrian
Distance estimation (m)
Object height (cm)
Distance
estimation (m)
Object height (cm)
Method for 3D obstacle detection in stereo
Detection
of 3D objects on the curved road surfaceRecognition of possible situation:
1) Object is on the surface; 2) Object is in the surface
Слайд 103
Автоматизированное конструирование алгоритмов обнаружения объектов
Постановка задачи
P1(R,A) → min(R,A) |
P2(R,A) ≤ P2max, T(R,A) ≤ Tmax
P1 – вероятность необнаружения объекта;
P2
– вероятность ложной тревоги;T – вычислительная стоимость алгоритма (время, ресурсы);
R – используемая морфологическая система;
A – алгоритм анализа данных.
Слайд 104Автоматизированное конструирование алгоритмов обнаружения объектов
1. Метод автоматизированного конструирования алгоритмов обнаружения
объектов, основанный на преобразованиях модельных описаний
Метод преобразования модельных описаний
Рекурсивные модели
и алгоритмыНерекурсивные модели и алгоритмы
Проективные морфологии на базе логического программирования
2. Метод автоматизированного конструирования модульных процедур обнаружения объектов, основанный на «генетическом отборе» элементов модельного описания
Общий подход к построению процедур идентификации
Учет информативности опорных элементов
Построение процедур идентификации объектов нескольких классов
Генетический отбор морфологических процедур
Слайд 105Автоматизированное конструирование алгоритмов обнаружения объектов
Конструирование детекторов по модельным описаниям
Формальное
описание моделей объектов.
Преобразование моделей объектов.
Перевод декларативного описания в процедурное (сопоставление
описанию объекта процедуры его обнаружения на изображении).Реализации полученных алгоритмов путем модификации типовых метаалгоритмов, соответствующих стандартным метамоделям.
Вероятностное описание моделей и расчет характеристик достоверности их обнаружения.
Учет программно-аппаратных характеристик типовых процедур (в заданной архитектуре вычислителя).
Статистический анализ результатов обработки изображения.
Слайд 106Метод преобразования модельных описаний
Модель объекта:
Преобразования моделей:
перестановка порядка предикатов;
декомпозиция (разбиение) модели
на две части
и редукция (отсечение) одной из них.
Obj = {
| }Автоматизированное конструирование алгоритмов обнаружения объектов Конструирование детекторов по модельным описаниям
Слайд 107Пример преобразования модельных описаний
Модели:
Штриховая линия = набор штрихов, лежащих на
одной прямой. (М1) Штриховая линия = прямая, состоящая из отдельных штрихов.
(М2)Процедуры: Найти все штрихи, выбрать те, что лежат на одной прямой. (П1) Последовательно находить штрихи, лежащие на одной прямой. (П2)
Автоматизированное конструирование алгоритмов обнаружения объектов Конструирование детекторов по модельным описаниям
Слайд 108Алгоритм применения построенной модели процедуры голосования:
1. Осуществить все возможные успешные
индексации целевого предиката на изображении.
2. Удалить все голосующие элементы, не участвующие
в найденных успешных индексациях целевого предиката.Результатом применения процедуры является морфологическая проекция изображения на модель объекта, заданную в запросе.
Автоматизированное конструирование алгоритмов обнаружения объектов
Конструирование детекторов по модельным описаниям
Слайд 109Проективные морфологии на базе неоднородных структурных моделей, описываемых логическими предикатами
Утверждение (достаточное условие построения проективного морфологического фильтра на базе логической
модели): Морфологическое преобразование на базе модели M является морфологическим проектором, если выполняется условие∀q: A(q)=0 ⇒ ∀A′(q)≠0: M(A(Q)VA(q))=M(A(Q)VA′(q)
(то есть в пользу M(A(Q)) голосуют только ненулевые элементы A(q)).
Морфологический проектор:
Pr(A(p),M)=Φ(A(p),M)=Φ(Φ(A(p),M),M)
Морфологический коэффициент корреляции изображения с моделью:
KM(A(p),M)=min(||Pr(A(p),M)||,||A(p)||) / max(||Pr(A(p),M)||,||A(p)||)
Автоматизированное конструирование алгоритмов обнаружения объектов
Конструирование детекторов по модельным описаниям
Слайд 110Принцип конструирования процедуры идентификации
Множество процедур обнаружения:
, где - процедура обнаружения фрагмента, реализующая один из заданных базовых алгоритмов (j=1,2,…,mk; k=1,2,3…).
Автоматизированное конструирование алгоритмов обнаружения объектов
Метод генетического отбора структурных моделей
Слайд 111Задача условной оптимизации:
,
где: - время работы процедуры на изображениях из обучающей выборки; - функция вычисления точности обнаружения объекта на изображении из обучающей выборки. При этом:
, - множество процедур длины не больше l,
Автоматизированное конструирование алгоритмов обнаружения объектов
Метод генетического отбора структурных моделей
Слайд 112Схема применения генетического алгоритма:
1. Ген = одна из элементарных процедур.
2.
Хромосома = последовательность генов ограниченной длины.
3. Функция качества хромосомы:
,,
где р - процедура обнаружения заданного объекта; Si - изображение из обучающей выборки; - время работы процедуры р на изображении Si; А – настроечный коэффициент; - штрафная функция.
4. Операция скрещивания – перегруппировка и обмен составных частей существующих решений (цепочек процедур обнаружения).
5. Операция мутации позволяет изменить параметры (xj,yj,wj,hj) для выбранной элементарной процедуры.
6. Генетический отбор осуществляется путем итеративного «размножения», тестирования и селекции в каждом поколении хромосом с наилучшим значением функции качества. При этом на каждом этапе случайным образом осуществляются мутации параметров и скрещивание моделей.
Автоматизированное конструирование алгоритмов обнаружения объектов
Метод генетического отбора структурных моделей
Слайд 113Схема применения генетического алгоритма для формирования морфологических детекторов:
1. Ген =
один из возможных структурных примитивов, характеризуемый набором {Mk(u,qk),tk,qk}.
2. Хромосома =
последовательность генов = морфо-геометрическая модель объекта M(p,u).3. Функция качества хромосомы - аналогично.
4. Операция скрещивания – аналогично.
5. Операция мутации позволяет изменить параметры локализации {Mk(u,qk),qk} для выбранного элемента модели.
6. Генетический отбор - аналогично.
Автоматизированное конструирование алгоритмов обнаружения объектов
Метод генетического отбора структурных моделей
Слайд 114Интерпретация результата:
1. Процедурная интерпретация = Близкая к оптимальной процедура обнаружения
заданного объекта.
2. Модельная интерпретация = Набор элементов структурной модели объекта,
на основе которой искомый объект может быть обнаружен и/или идентифицирован на изображениях из обучающей выборки.Автоматизированное конструирование алгоритмов обнаружения объектов
Метод генетического отбора структурных моделей
Слайд 115Conclusions
Two generic frameworks for image analysis and object detection
are presented.
It is important that they provide both theoretical basis
and practical techniques for engineers.A lot of commercial computer vision applications have been developed with the use of these techniques (just the small part of them is listed).
Different types of images and different application areas are covered by these approaches (in combination with other powerful techniques such as photogrammetry, motion analysis, character recognition and so on).
Thus, we can conclude that projective morphologies and evidence-based image analysis are effective enough and could be a part of modern applied computer vision.





























































![Development of Applied Computer Vision Systems Using Projective Morphologies and Evidence-Based Image Analysis Морфологический анализ свидетельств Вероятностная интерпретация методов морфологического анализа изображений Вероятностная модель формирования Морфологический анализ свидетельств Вероятностная интерпретация методов морфологического анализа изображений Вероятностная модель формирования образаP(M): Ω→[0,1],Вероятностная модель регистрации изображенияP(L/M): M→[0,1],Вероятностная модель искаженийP(A/L): M×Ω→[0,1]Критерий](/img/thumbs/3e743c5be7837a8c2f7fd5a67febde27-800x.jpg)