Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Pressure
Содержание
- 1. Pressure
- 2. Fluid MechanicsA fluid is a collection of
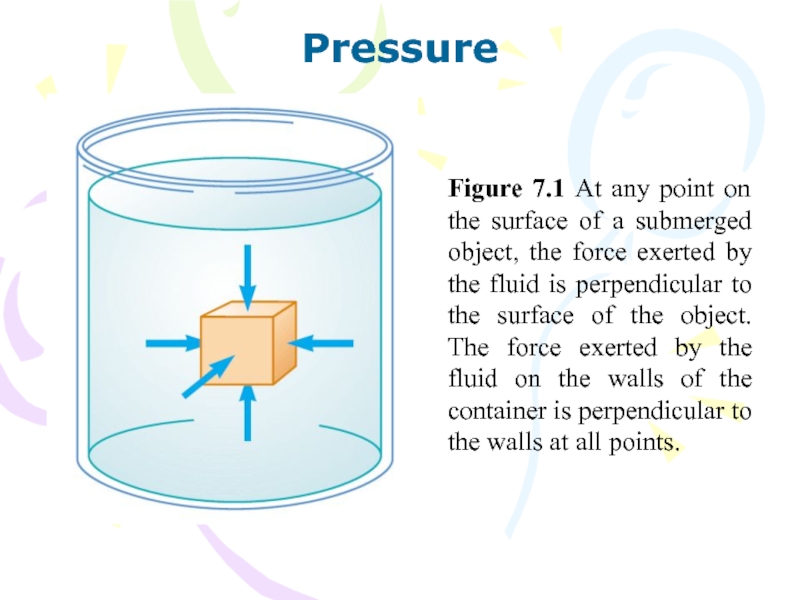
- 3. Figure 7.1 At any point on the
- 4. PressureFigure 7.2 A simple device for measuring
- 5. If the pressure varies over an area,
- 6. Snowshoes keep you from sinking into soft
- 7. Table 7.1Variation of Pressure with Depth
- 8. Variation of Pressure with DepthFigure 7.3 A
- 9. Variation of Pressure with DepthThat is, the
- 10. If the liquid is open to the
- 11. Figure 7.4 (a) Diagram of a hydraulic
- 12. (b)Figure 7.4 (a) Diagram of a hydraulic
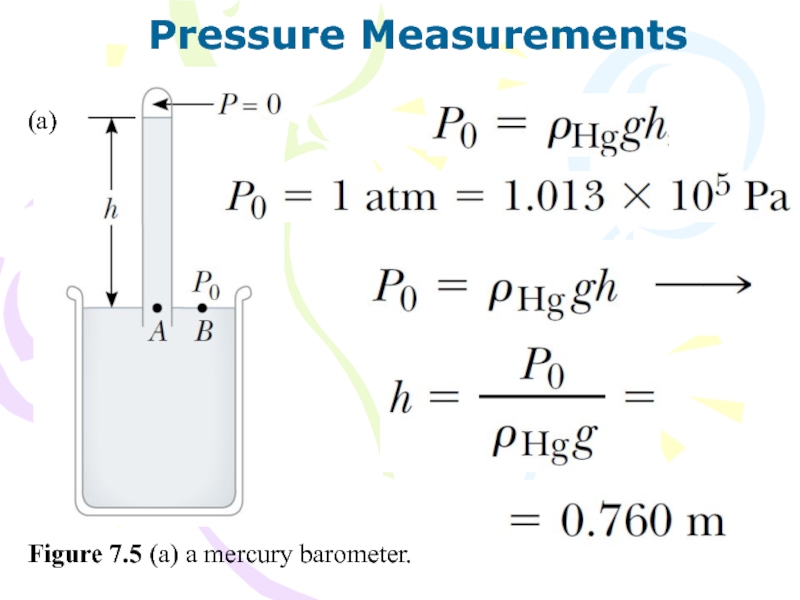
- 13. Pressure MeasurementsFigure 7.5 (a) a mercury barometer.(a)
- 14. Pressure MeasurementsFigure 7.5 (b) an open-tube manometer.(b)The
- 15. Buoyant Forces and Archimedes’s PrincipleFigure 7.6 (a)
- 16. The upward force exerted by a fluid
- 17. Buoyant Forces and Archimedes’s PrincipleFigure 7.7 The
- 18. Case 1: Totally Submerged ObjectFigure 7.8 The
- 19. Thus, the direction of motion of an
- 20. Figure 7.9 An object floating on the
- 21. This equation tells us that the fraction
- 22. Fluid DynamicsWhen fluid is in motion, its
- 23. Figure 7.11 Hot gases from a cigarette
- 24. Fluid DynamicsThe term viscosity is commonly used
- 25. Fluid DynamicsBecause the motion of real fluids
- 26. The path taken by a fluid particle
- 27. Fluid DynamicsFigure 7.13 A fluid moving with
- 28. Fluid DynamicsThis expression is called the equation
- 29. Bernoulli’s EquationFigure 7.14 A fluid in laminar
- 30. Bernoulli’s Equation
- 31. Bernoulli’s EquationThis is Bernoulli’s equation as applied to an ideal fluid. It is often expressed as(7.8)(7.9)
- 32. Bernoulli’s EquationThis Bernoulli effect explains the experience
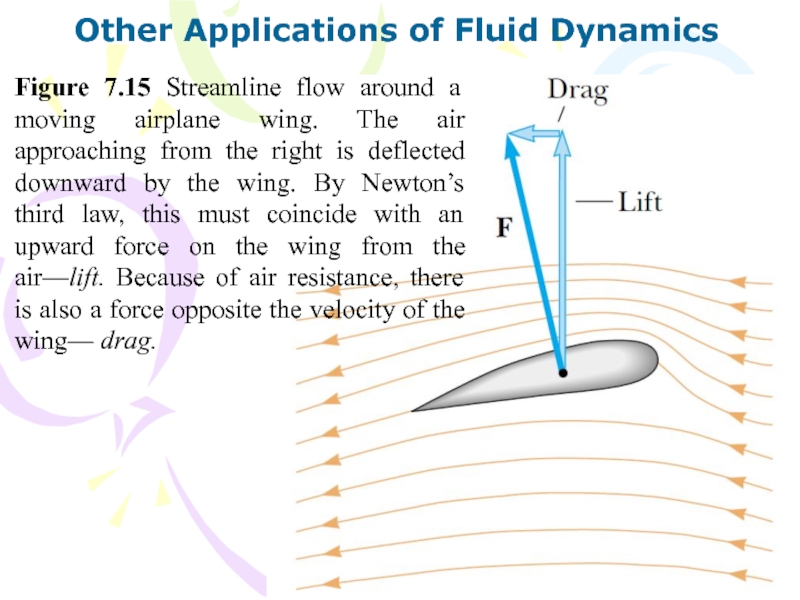
- 33. Other Applications of Fluid DynamicsFigure 7.15 Streamline
- 34. Other Applications of Fluid DynamicsFigure 7.16 Because
- 35. Other Applications of Fluid DynamicsFigure 7.17 A
- 36. Quick Quiz 7.1 Suppose you are standing
- 37. Quick Quiz 7.2 The pressure at the
- 38. Quick Quiz 7.3 Several common barometers are
- 39. Quick Quiz 7.4 An apple is held
- 40. Quick Quiz 7.5 You observe two helium
- 41. Quick Quiz 7.6 You tape two different
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Course of lectures «Contemporary Physics: Part1»
Lecture №9
Fluid Mechanics.
Pressure. Variation
Слайд 2Fluid Mechanics
A fluid is a collection of molecules that are
randomly arranged and held together by weak cohesive forces and
by forces exerted by the walls of a container. Both liquids and gases are fluids.In our treatment of the mechanics of fluids, we do not need to learn any new physical principles to explain such effects as the buoyant force acting on a submerged object and the dynamic lift acting on an airplane wing. First, we consider the mechanics of a fluid at rest—that is, fluid statics. We then treat the mechanics of fluids in motion— that is, fluid dynamics. We can describe a fluid in motion by using a model that is based upon certain simplifying assumptions.
Слайд 3Figure 7.1 At any point on the surface of a
submerged object, the force exerted by the fluid is perpendicular
to the surface of the object. The force exerted by the fluid on the walls of the container is perpendicular to the walls at all points.Pressure
Слайд 4Pressure
Figure 7.2 A simple device for measuring the pressure exerted
by a fluid.
If F is the magnitude of the force
exerted on the piston and A is the surface area of the piston, then the pressure P of the fluid at the level to which the device has been submerged is defined as the ratio F/A:(7.1)
Note that pressure is a scalar quantity because it is proportional to the magnitude of the force on the piston.
Слайд 5If the pressure varies over an area, we can evaluate
the infinitesimal force dF on an infinitesimal surface element of
area dA aswhere P is the pressure at the location of the area dA. The pressure exerted by a fluid varies with depth. Therefore, to calculate the total force exerted on a flat vertical wall of a container, we must integrate Equation 7.2 over the surface area of the wall.
(7.2)
Because pressure is force per unit area, it has units of newtons per square meter (N/m2) in the SI system. Another name for the SI unit of pressure is pascal (Pa):
(7.3)
Слайд 6Snowshoes keep you from sinking into soft snow because they
spread the downward force you exert on the snow over
a large area, reducing the pressure on the snow surface.Слайд 8Variation of Pressure with Depth
Figure 7.3 A parcel of fluid
(darker region) in a larger volume of fluid is singled
out. The net force exerted on the parcel of fluid must be zero because it is in equilibrium.Слайд 9Variation of Pressure with Depth
That is, the pressure P at
a depth h below a point in the liquid at
which the pressure is P0 is greater by an amount ρgh.(7.4)
Слайд 10If the liquid is open to the atmosphere and P0
is the pressure at the surface of the liquid, then
P0 is atmospheric pressure. In our calculations and working of end-of-chapter problems, we usually take atmospheric pressure to beIn view of the fact that the pressure in a fluid depends on depth and on the value of P0, any increase in pressure at the surface must be transmitted to every other point in the fluid. This concept was first recognized by the French scientist Blaise Pascal (1623–1662) and is called Pascal’s law: a change in the pressure applied to a fluid is transmitted undiminished to every point of the fluid and to the walls of the container.
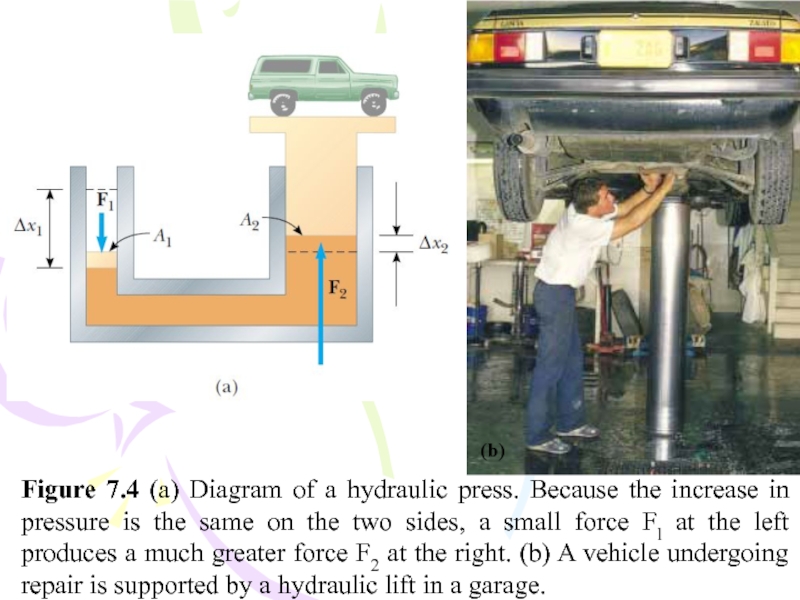
Слайд 11Figure 7.4 (a) Diagram of a hydraulic press. Because the
increase in pressure is the same on the two sides,
a small force Fl at the left produces a much greater force F2 at the right.Слайд 12(b)
Figure 7.4 (a) Diagram of a hydraulic press. Because the
increase in pressure is the same on the two sides,
a small force Fl at the left produces a much greater force F2 at the right. (b) A vehicle undergoing repair is supported by a hydraulic lift in a garage.Слайд 14Pressure Measurements
Figure 7.5 (b) an open-tube manometer.
(b)
The difference in pressure
P - P0 is equal to ρgh. The pressure P
is called the absolute pressure, while the difference P - P0 is called the gauge pressure. For example, the pressure you measure in your bicycle tire is gauge pressure.Слайд 15Buoyant Forces and Archimedes’s Principle
Figure 7.6 (a) A swimmer attempts
to push a beach ball underwater. (b) The forces on
a beach ball–sized parcel of water. The buoyant force B on a beach ball that replaces this parcel is exactly the same as the buoyant force on the parcel.(b)
(a)
Слайд 16The upward force exerted by a fluid on any immersed
object is called a buoyant force.
Buoyant Forces and Archimedes’s Principle
The
magnitude of the buoyant force always equals the weight of the fluid displaced by the object. This statement is known as Archimedes’s principle.Слайд 17Buoyant Forces and Archimedes’s Principle
Figure 7.7 The external forces acting
on the cube of liquid are the gravitational force Fg
and the buoyant force B. Under equilibrium conditions, B = Fg .(7.5)
Слайд 18Case 1: Totally Submerged Object
Figure 7.8 The external forces acting
on the cube of liquid are the gravitational force Fg
and the buoyant force B. Under equilibrium conditions, B = Fg .(b)
(a)
Слайд 19Thus, the direction of motion of an object submerged in
a fluid is determined only by the densities of the
object and the fluid.Case 1: Totally Submerged Object
Слайд 20Figure 7.9 An object floating on the surface of a
fluid experiences two forces, the gravitational force Fg and the
buoyant force B. Because the object floats in equilibrium, B = Fg .Case 2: Floating Object
Слайд 21This equation tells us that the fraction of the volume
of a floating object that is below the fluid surface
is equal to the ratio of the density of the object to that of the fluid.(7.6)
Case 2: Floating Object
Слайд 22Fluid Dynamics
When fluid is in motion, its flow can be
characterized as being one of two main types. The flow
is said to be steady, or laminar, if each particle of the fluid follows a smooth path, such that the paths of different particles never cross each other. In steady flow, the velocity of fluid particles passing any point remains constant in time.Figure 7.10 Laminar flow around an automobile in a test wind tunnel.
Слайд 23Figure 7.11 Hot gases from a cigarette made visible by
smoke particles. The smoke first moves in laminar flow at
the bottom and then in turbulent flow above.Above a certain critical speed, fluid flow becomes turbulent; turbulent flow is irregular flow characterized by small whirlpool-like regions, as shown in Figure 7.11.
Fluid Dynamics
Слайд 24Fluid Dynamics
The term viscosity is commonly used in the description
of fluid flow to characterize the degree of internal friction
in the fluid. This internal friction, or viscous force, is associated with the resistance that two adjacent layers of fluid have to moving relative to each other. Viscosity causes part of the kinetic energy of a fluid to be converted to internal energy. This mechanism is similar to the one by which an object sliding on a rough horizontal surface loses kinetic energy.Слайд 25Fluid Dynamics
Because the motion of real fluids is very complex
and not fully understood, we make some simplifying assumptions in
our approach. In our model of ideal fluid flow, we make the following four assumptions:1. The fluid is nonviscous. In a nonviscous fluid, internal friction is neglected. An object moving through the fluid experiences no viscous force.
2. The flow is steady. In steady (laminar) flow, the velocity of the fluid at each point remains constant.
3. The fluid is incompressible. The density of an incompressible fluid is constant.
4. The flow is irrotational. In irrotational flow, the fluid has no angular momentum about any point. If a small paddle wheel placed anywhere in the fluid does not rotate about the wheel’s center of mass, then the flow is irrotational.
Слайд 26The path taken by a fluid particle under steady flow
is called a streamline. The velocity of the particle is
always tangent to the streamline, as shown in Figure 7.12. A set of streamlines like the ones shown in Figure 7.12 form a tube of flow. Note that fluid particles cannot flow into or out of the sides of this tube; if they could, then the streamlines would cross each other.Fluid Dynamics
Figure 7.12 A particle in laminar flow follows a streamline, and at each point along its path the particle’s velocity is tangent to the streamline.
Слайд 27Fluid Dynamics
Figure 7.13 A fluid moving with steady flow through
a pipe of varying cross-sectional area. The volume of fluid
flowing through area A1 in a time interval ∆t must equal the volume flowing through are A2 in the same time interval. Therefore, A1v1 = A2v2.Слайд 28Fluid Dynamics
This expression is called the equation of continuity for
fluids. It states that
the product of the area and the
fluid speed at all points along a pipe is constant for an incompressible fluid.(7.7)