Аксиоматика Гильберта. Следствия из аксиом Д.Гильберта

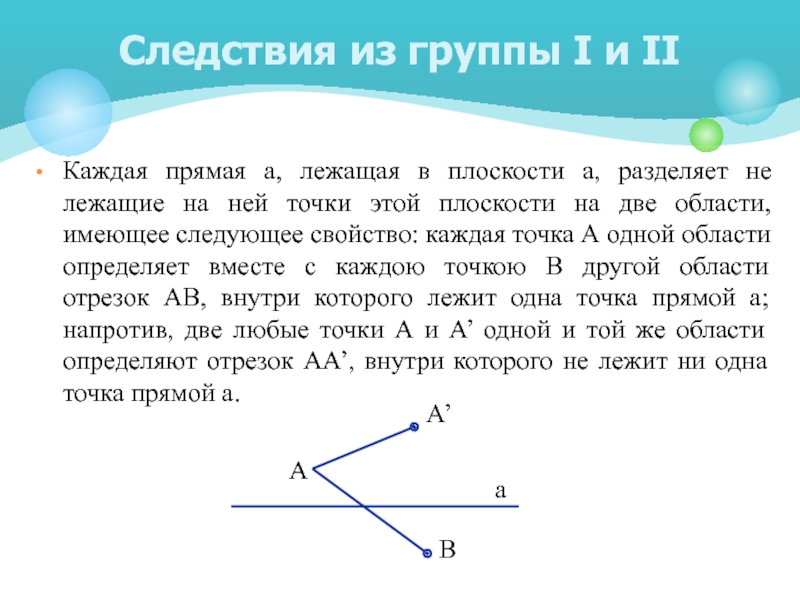
плоскость.
Есть также 3 элементарных бинарных отношения:
Лежать между, применимо к

точкам;
Содержать, применимо к точкам и прямым, точкам и плоскостям или прямым и плоскостям;
Конгруэнтность (геометрическое равенство), применимо, например, к отрезкам, углам или треугольникам, и обозначается символом ≅.
Все точки, прямые и плоскости предполагаются различными, если не оговорено особое.

стереометрические
аксиомы порядка:
линейные
Аксиома Паша
аксиомы конгруэнтности:
конгруэнтность отрезков
конгруэнтность углов
аксиомы непрерывности:
Аксиома

Архимеда
Аксиома Кантора
аксиома параллельности.

Структура аксиоматики

лежит не менее двух точек.
3. Существуют по крайней мере

три точки, не лежащие на одной прямой.
4. Через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну.
5. В каждой плоскости лежит по крайней мере одна точка.
6. Если две точки прямой лежат в некоторой плоскости, то и все точки ее лежат в той же плоскости.
7. Если две плоскости имеют одну общую точку, то они имеют еще хотя бы одну общую точку.
8. Существуют по крайней мере четыре точки, не лежащие на одной плоскости.

Аксиомы группы I

общей точки.
Теорема 2. Две плоскости либо совсем не имеют общих

точек, либо имеют общую прямую, на которой лежат все их общие точки.
Теорема 3. Плоскость и не лежащие на ней прямая не могут иметь более одной общей точки.
Теорема 4. Через прямую и не лежащую на ней точку, или через две различные прямы с общей точкой проходит одна и только одна плоскость.
Теорема 5. На каждой плоскости существует по меньшей мере три точки, не лежащие на одной прямой.

Следствия из группы I

и С, то А, В и С - различные точки

прямой и В лежит также между С и А.
2. При данных двух точках А и В на прямой линии существует по крайней мере одна такая точка С, что В лежит между А к С.
3. Из трех данных точек на прямой не более чем одна лежит между двумя другими.
4. Аксиома Паша. Если в данной плоскости даны треугольник АВС и какая-нибудь прямая l, не проходящая через одну из его вершин и пересекающая сторону АВ, то эта прямая непременно пересечет одну из двух других сторон АС или ВС.

Аксиомы группы II

любых 3-х точек А, В, С одной прямой всегда существует

одна, лежащая между 2-мя другими.
Если некоторая прямая а пересекает каких - либо два из трёх отрезков АВ, ВС и АС, то она не пересекает третий.
Если В лежит на отрезке АС и С на отрезке ВD, то В и С лежат на отрезке AD.
Если даны четыре точки прямой, то они могут быть всегда так обозначены буквами А, В, С, D, что точка В лежит как между А и С, так и между А и D; а точка С как между А и D, так и между В и D.

Следствия из группы I и II

на ней точки этой плоскости на две области, имеющее следующее

свойство: каждая точка А одной области определяет вместе с каждою точкою В другой области отрезок АВ, внутри которого лежит одна точка прямой а; напротив, две любые точки А и А’ одной и той же области определяют отрезок АА’, внутри которого не лежит ни одна точка прямой а.

Следствия из группы I и II

отложить отрезок, равный данному.
2. Два отрезка, равные третьему, равны между

собой.
3. Пусть А, В, С — точки одной прямой и К, L, М —также точки одной прямой. Пусть, кроме того, АВ = KL, ВС = LМ. Если отрезки АВ и ВС, а также КL и LМ не имеют общих точек, то АС = КМ.
4. От любой точки данной прямой по данную сторону можно построить один и только один угол, равный данному. Каждый угол равен самому себе.
5. Если в двух треугольниках AВС и КLМ стороны АВ = КL, АС = КМ и ВАС = LKM, то АВС = КLМ.

Аксиомы группы III

рядах точек А,В,…, K, L и A’, B’,…, K’,L’ точки

первого расположены так, что В лежит между А с одной стороны и C, D,…, K, L с другой. С между А, В с одной стороны и D,…, K, L с другой и т.д., то и точки A’, B’,…, K’, L’ расположены таким же образом, т.е. B’ лежит между A’ с одной стороны и C’, D’,…, K’, L’ с другой, C’ лежит между A’, B’ с одной стороны и D’,…, K’, L’ с другой и т.д.
Теорема 2. Если ≡ и ≡ , то также всегда ≡ .

Следствия из группы III

ВС = В’C’ и A = A, mo

∆АВС = ∆А'В'С'
Если для ∆АВС и ∆А'В'С', АВ = А'В’, ,
, то ∆АВС = ∆А'В'С'.
Если для ∆АВС и ∆А'В'С', АВ = А'В', ВС = В'С', АС = А'С', то ∆АВС = ∆А'В'С'.
Внешний угол треугольника больше всякого внутреннего, не смежного с ним.
В равнобедренном треугольнике углы при основании равны.

Следствия из группы III

теорема о конгруэнтности треугольников). Если в двух треугольниках три стороны

одного соответственно конгруэнтны трем сторонам другого, то треугольники конгруэнтны.

Теорема 6 выражает тот важный результат, что все пространственные предложения о конргуэнтности, а следовательно, и о движении в пространстве, суть следствия пяти линейных и плоскостных аксиом конгруэнтности, если присовокупить сюда I и II группы аксиом.

Следствия из группы III

треугольников АВС и А'В'С' удовлетворены конгруэнции:
АВ≡A'B', AC≡A'C', ≡

, то оба треугольника взаимно конгруэнтны.
Теорема 2. (Вторая теорема о конгруэнтности треугольников). Если в двух треугольниках соответственно конгруэнтны между собою сторона и оба прилежащие к ней угла, то треугольники конгруэнтны.
Теорема 3. Если два угла и взаимно конгруэнтны, то и смежные им углы и тоже взаимно конгруэнтны.

Следствия из группы III

существует число n и n точек A1,…,An на AB таких,

что: AjAj+1 ≅ CD, 1≤j

Аксиома Кантора. Пусть на прямой a дана бесконечная последовательность отрезков A1B1, A2B2,…, такая, что каждый последующий есть часть предыдущего и для любого наперед заданного отрезка CD найдется n N такое, что AnBn

Аксиомы группы IV

не более одной прямой, параллельной данной.
Аксиома группы V

предложениям.

Теорема 1. Если две параллельные пересечены третьей прямой, то накрестлежащие

соответственные углы равны, и обратно: конгруэнтность накрестлежащих или соответственных углов имеет следствием параллельность прямых.

Теорема 2. Сумма углов треугольника равна двум прямым.

на прямой можно присвоить имена A, B, C, и D

так, чтобы точка B лежала между точками A и C, а также между A и D; точка C — между A и D, а также между B и D.»
Э.Х. Мур (англ.) доказал в 1902 году, что эта аксиома избыточна.

21 аксиома

становится бесконечно малым, то превращается в точку. Тогда человек говорит:

"Это моя точка зрения".

которые разделены на … групп:
1) аксиомы……………………………………………...;
2) аксиомы……………………………………………...;
3) аксиомы…....................................................................;
4) аксиомы ……………………………………………..;
5)

аксиома……………………………………………….

Паша?
1) аксиомы непрерывности;
2) аксиомы конгруэнтности;
3) аксиомы порядка;
4) аксиомы принадлежности.

левым и правым столбцами.
А) На любой прямой от любой

ее точки можно отложить отрезок, равный данному.
Б) Две точки определяют только одну прямую.
В) Если даны отрезок CD и луч AB, то существует число n и n точек A1,…,An на AB таких, что: AjAj+1 ≅ CD, 1≤jГ) Из трех данных точек на прямой не более чем одна лежит между двумя другими.

Аксиомы принадлежности;
Аксиомы порядка;
Аксиомы конгруэнтности;
Аксиомы непрерывности

аксиом, которые разделены на 5 групп:
1) Аксиомы принадлежности;
2) Аксиомы порядка;
3)

Аксиомы конгруэнтности;
4) Аксиомы непрерывности;
5) Аксиома параллельности.
2. 3) аксиомы порядка
3. 1-Б, 2-Г, 3-А, 4-В