РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

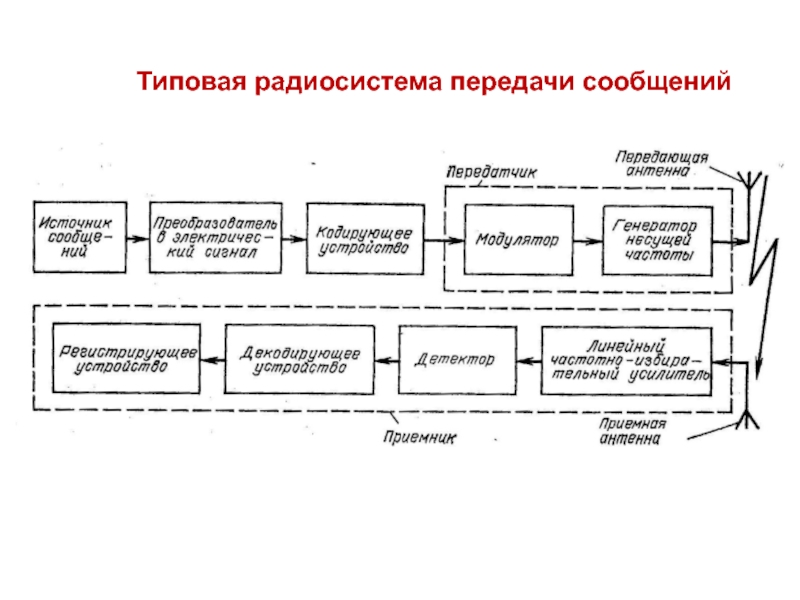
и сигналы" (РЦС) формирует базовую теоретическую подготовку в области телекоммуникационных

систем, являясь продолжением дисциплины "Теория электрических цепей».

Предметом изучения в курсе РЦС являются математические модели сигналов и физических процессов, происходящих при их преобразовании в радиотехнических устройствах, а также алгоритмы этих преобразований.

является формирование следующих профессиональных компетенций:
способность самостоятельного анализа свойств радиотехнических

сигналов;
способность самостоятельного синтеза и анализа типовых радиотехнических цепей и устройств;
способность применять современные математические методы исследования с использованием компьютерной техники;
способность проводить математическое моделирование процессов и объектов на базе стандартных пакетов автоматизированного проектирования и исследований.

сигналом называют физический носитель сообщения, то есть информации, предназначенной для

передачи.
Для того, чтобы сделать сигнал объектом теоретического изучения вводят математическую модель сигнала – способ его математического описания, представляющий собой функциональную зависимость, аргументом которой, как правило, является время – s(t), x(t), u(t).
Математическая модель позволяет абстрагироваться от физической природы носителя сообщения и описывает наиболее существенные свойства сигнала.
Введение математической модели позволяет провести классификацию сигналов.

Определение сигнала

произвольный по величине и непрерывный во времени. Аналоговый сигнал x(t)

описывается непрерывной или кусочно-непрерывной функцией времени. Аргумент и сама функция принимают любые значения на интервале

величине значения в дискретные моменты времени.
Дискретный

сигнал хД (t) описывается решётчатой функцией – последовательностью выборочных значений (отсчетов) в соответствующие моменты времени:



Интервал Δt
называется
интервалом
дискретизации.

обратную ей – частотой дискретизации:



В этом случае значения решётчатой функции

записываются как х(nTД), х(n) или просто xn. Таким образом, дискретный сигнал записывается как

Дискретные сигналы

по уровню дискретный сигнал.
Он описывается

квантованными решетчатыми функциями (квантованными последовательностями отсчетных значений), принимающими конечный ряд дискретных значений d0, d1, ... dk, называемых уровнями квантования.
Связь между решетчатой функцией хД(nTД) и квантованной решетчатой функцией хЦ(nTД) определяется нелинейной функцией – амплитудной характеристикой квантования Q(x)

Цифровые сигналы

сигналы

операций квантования и кодирования

Связи между сигналами

sin(t)
0

0
0.4189 0.40674
0.8378 0.74314
1.2566 0.95106
1.6755 0.99452
2.0944 0.86603
2.5133 0.58779
2.9322 0.20791
3.3510 -0.20791
3.7699 -0.58779
4.1888 -0.86603
4.6077 -0.99452
5.0265 -0.95106
5.4454 -0.74314
5.8643 -0.40674
6.2832 -2.45e-016

sin(t)
0

0
0.4189 0.40674
0.8378 0.74314
1.2566 0.95106
1.6755 0.99452
2.0944 0.86603
2.5133 0.58779
2.9322 0.20791
3.3510 -0.20791
3.7699 -0.58779
4.1888 -0.86603
4.6077 -0.99452
5.0265 -0.95106
5.4454 -0.74314
5.8643 -0.40674
6.2832 -2.45e-016

sin(t)
0

0
0.4189 0.40674
0.8378 0.74314
1.2566 0.95106
1.6755 0.99452
2.0944 0.86603
2.5133 0.58779
2.9322 0.20791
3.3510 -0.20791
3.7699 -0.58779
4.1888 -0.86603
4.6077 -0.99452
5.0265 -0.95106
5.4454 -0.74314
5.8643 -0.40674
6.2832 -2.45e-016