Преодоление неопределенностей целей

Содержание

1. Преодоление неопределенностей целей
2. Пример «Строительство аэропорта»КритерииСтоимость строительстваРасстояние от городаМинимальное шумовое воздействие
3. Пример (альтернативы)А: $ 100 млн; 20 мин;
4. МКЗ(Ω, {fi}n, {⎬,~}),где {fi}n - n целевых
5. МКЗ 1. Цели взаимно нейтральны
6. Цели нейтральны
7. Алгоритм решения МКЗуменьшить исходное множество альтернатив, убрав
8. МКЗx1
9. Принцип ПаретоПусть x1 и x2 – альтернативы.
10. Множество ПаретоОставшиеся альтернативы образуют множество Парето -
11. Множество Паретоили таких, улучшение которых по одним
12. Критериальное пространство В критериальном пространстве альтернативы
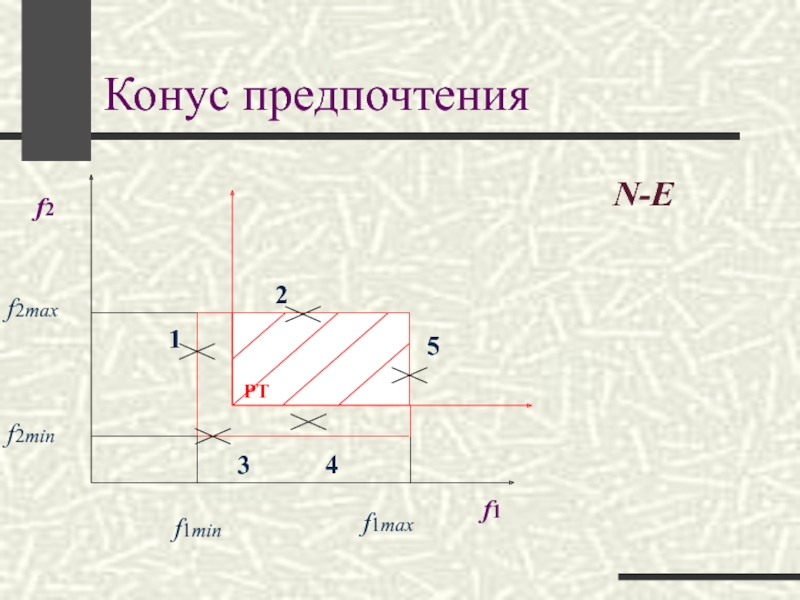
13. Конус предпочтения
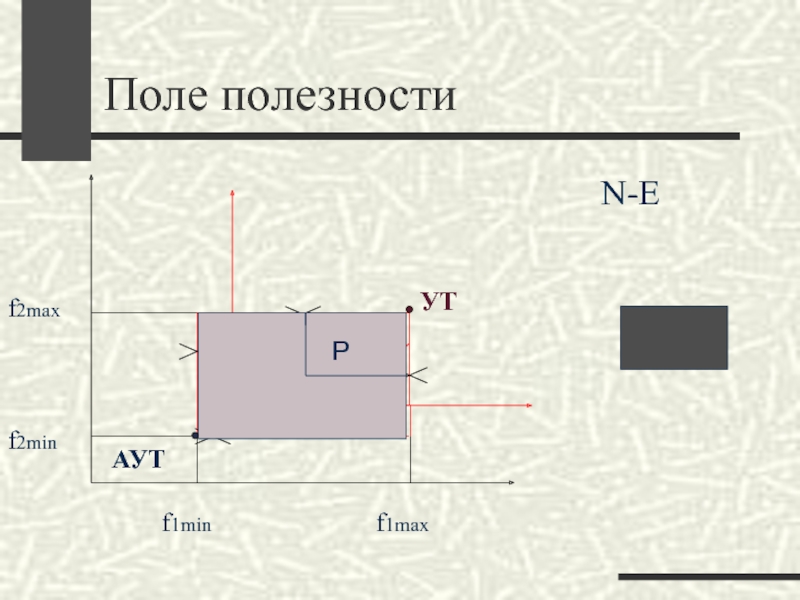
14. Поле полезности
15. Способы задания альтернативкоординатный (альтернативы заданы своими
16. Множество ПаретоХ1(2;7)Х2(4;4)Х3(3;6)Х4(7;1) Х5(5;3)Х6(6;0)Х7(4;3)═>
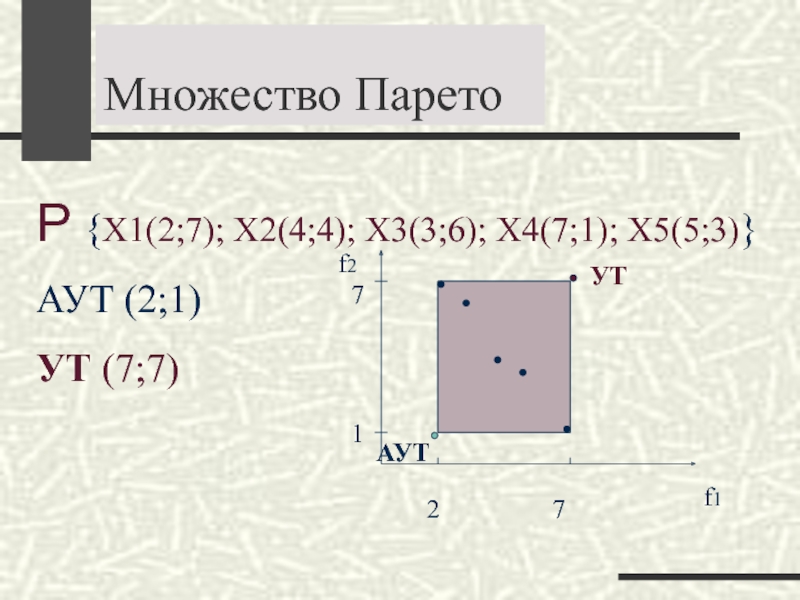
17. Множество ПаретоР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}АУТ (2;1)УТ (7;7)7127f1f2АУТУТ
18. Множество Парето
19. Множество Парето
20. Множество ПаретоВсе альтернативы из множества Парето являются
21. Перевод в однородную шкалуfi*(x) - оценка альтернативы
22. Перевод в однородную шкалуА: $
23. Принятие решений при неопределенности целейИнтегральный критерийМетод НэшаМетод контрольных показателейПростейший методВведение метрики в пространстве целевых функцийСверткаMAUT
24. Интегральный критерий x (f1(х), f2(х),
25. Метод арбитражных решений, или метод НэшаАУТ( )F(x)=
26. ПримерР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}F(x1)=(2-2)(7-1)=0F(x2)=(4-2)(4-1)=6F(x3)=(3-2)(6-1)=5F(x4)=(7-2)(1-1)=0F(x5)=(5-2)(3-1)=6АУТ (2;1)х2 ~ х5 по Нэшу
27. Использование контрольных показателей {fi*}n, fi (x) ≥ fi*,
28. ПримерР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}Пусть f1*=3; f2*=2 АУТ (2;1)F(x2)=min{4/3; 4/2}=4/3F(x3)=min{3/3; 6/2}=1F(x5)=min{5/3; 3/2}=3/2
29. Простейший способРанг, равный 1, присваивается главному критерию
30. Введение метрики в пространстве целевых функцийУТ(fimax)
31. ПримерР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}h(x1)=5h(x2)=√18, h(x3)= √17h(x4)=6h(x5)= √20
32. ПримерА: $ 100 млн; 20 мин; 50
33. Cвертказдесь x – альтернатива из множества Парето fi(x) – оценка альтернативы x по i-му критерию
34. СверткаCi – коэффициенты относительной важности критериев
35. Экспертное оценивание Пусть rij – ранг, который
36. Экспертное оценивание Тогда коэффициент значимости i-го критерия с точки зрения j–го экспертаCi
37. Экспертное оцениваниеПусть gj – компетентность j–го эксперта, тогда Ci
38. Оценивание Th. Если
39. Пример
40. Использование линейной свертки Это задачи, связанные с
41. Квадратичная свертка
42. Свертка порядка t Величина t, стоящая
43. недопустима никакая компенсация, и требуется выравнивание значений
44. 3/8 2/8 2/8 1/8
45. t→0 -
46. В задачах планирования ударов «по узкому месту»
47. 3/8 2/8 2/8 1/8
48. Свертка Используя в качестве интегрального критерия
49. Multi-Attribute Utility Theory (MAUT)Используется при возможном структурировании
50. Алгоритм MAUTОценивается частичная полезность каждой альтернативы по
51. Пример: «Выбор местоположения предприятия»МестоположениеЗУМестоположениеПМРиТВГРЗУЦЗУРОППКРТИТЭФППсПБУМССНД0.20.350.250.20.30.50.20.60.40.40.20.250.150.60.4А, Б, С
52. Оценка частичной полезности альтернатив по критериюРЗУ, тыс.
53. Показатели частичной полезностиU(A)=0,06-0,04+0,06+0,02+0,0375+0,0375+0,048+0,48=0,703U(Б)=0,012-0,1+0,126+0,112+0,0625+0,12+0,08=0,4125U(C)=-0,06-0,032+0,21+0,14+0,1+0,05+0,03=0,438
54. Применение«+»: Относительно простой способ нахождения решения в
55. Слайд 55
56. Скачать презентанцию

Пример «Строительство аэропорта»КритерииСтоимость строительстваРасстояние от городаМинимальное шумовое воздействие

Главная
Разное
Преодоление неопределенностей целей

Слайды и текст этой презентации

Слайд 1Принятие решений при неопределенности целей
1 Постановка многокритериальной задачи
2 Множество Парето.

Поле полезности решений.
Конус предпочтения

Принятие решений при неопределенности целей1 Постановка многокритериальной задачи2 Множество Парето. Поле полезности решений. Конус предпочтения

Слайд 2Пример «Строительство аэропорта»
Критерии
Стоимость строительства
Расстояние от города
Минимальное шумовое воздействие

Слайд 3Пример (альтернативы)
А: $ 100 млн; 20 мин; 50 тыс. чел;
Б:

$ 130 млн; 30 мин; 20 тыс чел;
С: $ 200

млн; 60 мин; 5 тыс чел;

Пример (альтернативы)А: $ 100 млн; 20 мин; 50 тыс. чел;Б: $ 130 млн; 30 мин; 20 тыс

Слайд 4МКЗ
(Ω, {fi}n, {⎬,~}),
где {fi}n - n целевых функций fi, каждая

из которых сформулирована в виде fi(х)→max

х
⎬ - отношение предпочтения
~ - отношение эквивалентности

Слайд 5МКЗ
1. Цели взаимно нейтральны

2. Цели кооперируются

3. Цели конкурируют

Цели

могут находиться друг с другом в различных отношениях:

МКЗ 1. Цели взаимно нейтральны 2. Цели кооперируются3. Цели конкурируютЦели могут находиться друг с другом в различных

Слайд 6 Цели нейтральны

xЄΩ1

…

xЄΩ

xЄΩn-1

Слайд 7Алгоритм решения МКЗ
уменьшить исходное множество альтернатив, убрав заведомо худшие
свести задачу

к однокритериальной путем введения интегрального критерия

Алгоритм решения МКЗуменьшить исходное множество альтернатив, убрав заведомо худшиесвести задачу к однокритериальной путем введения интегрального критерия

Слайд 8МКЗ
x1 (f1(x1), f2(x1), …,

fn(x1))

x2 (f1(x2), f2(x2),

…, fn(x2))

Слайд 9Принцип Парето
Пусть x1 и x2 – альтернативы.

Если для i fi(x1) ≥

fi(x2),
причем хотя бы одно неравенство строгое,
то x1x2,
и альтернативу х2 можно исключить из рассмотрения

Принцип ПаретоПусть x1 и x2 – альтернативы. Если для i

Слайд 10Множество Парето
Оставшиеся альтернативы образуют множество Парето -
множество

неулучшаемых альтернатив, или
множество несравнимых альтернатив,

Множество ПаретоОставшиеся альтернативы образуют множество Парето - множество неулучшаемых альтернатив, или множество несравнимых альтернатив,

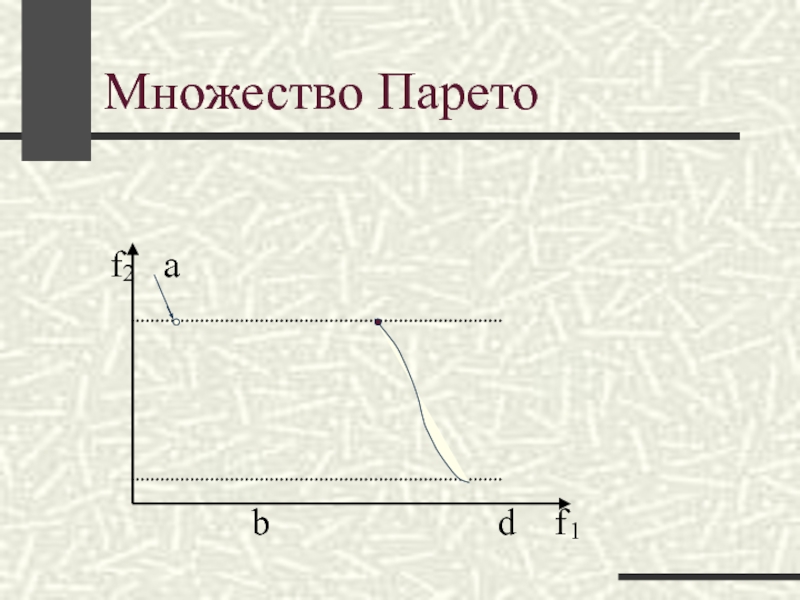
Слайд 11Множество Парето
или таких,
улучшение которых по одним критериям приводит к

их ухудшению по другим
Возможные решения следует искать лишь среди неулучшаемых

альтернатив

Множество Паретоили таких, улучшение которых по одним критериям приводит к их ухудшению по другимВозможные решения следует искать

Слайд 12Критериальное пространство
В критериальном пространстве альтернативы

заданы точками,
проекции которых

на оси являются оценками альтернатив по соответствующим критериям.

Критериальное пространство В критериальном пространстве альтернативы заданы точками,

Слайд 13Конус предпочтения

N-E

РТ

f2max

f2min

f1min

f1max

Слайд 14Поле полезности

N-E

f1max

f2max

f1min

f2min

АУТ

УТ

Слайд 15Способы задания альтернатив
координатный
(альтернативы заданы своими координатами в

критериальном пространстве)
графический
(альтернативы образуют непрерывное множество и изображены точками

на графике в координатном пространстве)
аналитический
(оценки альтернатив по каждому критерию являются непрерывными функциями, например, f1(x)=x, f2(x)=x3-4x+2)

Способы задания альтернативкоординатный (альтернативы заданы своими координатами в критериальном пространстве)графический (альтернативы образуют непрерывное множество и

Слайд 16Множество Парето
Х1(2;7)
Х2(4;4)
Х3(3;6)
Х4(7;1)
Х5(5;3)
Х6(6;0)
Х7(4;3)

═>

Слайд 17Множество Парето
Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}
АУТ (2;1)
УТ (7;7)

7
1
2
7
f1
f2

АУТ
УТ

Слайд 18Множество Парето

Слайд 19Множество Парето

Слайд 20Множество Парето
Все альтернативы из множества Парето являются решением многокритериальной задачи

в смысле этого принципа, т.е. являются паретооптимальными
Основным недостатком таких

решений является их множественность

Множество ПаретоВсе альтернативы из множества Парето являются решением многокритериальной задачи в смысле этого принципа, т.е. являются паретооптимальными

Слайд 21Перевод в однородную шкалу
fi*(x) - оценка альтернативы x по i-му

критерию в «родной» шкале
fimax и fimin - максимальное

и минимальное значения альтернатив по i-му критерию

Перевод в однородную шкалуfi*(x) - оценка альтернативы x по i-му критерию в «родной» шкале fimax и

Слайд 22Перевод в однородную шкалу
А: $ 100 млн; 20

мин; 50 тыс. чел;
Б: $ 130 млн;

30 мин; 20 тыс чел;
С: $ 200 млн; 60 мин; 5 тыс чел;

А(0;0;-1) Б(-3/10;-1/4;-1/3) С(-1;-1;0)
УТ(0;0;0) АУТ(-1;-1;-1)

Перевод в однородную шкалуА: $ 100 млн; 20 мин; 50 тыс. чел;Б:

Слайд 23Принятие решений при неопределенности целей
Интегральный критерий
Метод Нэша
Метод контрольных показателей
Простейший метод
Введение

метрики в пространстве целевых функций
Свертка
MAUT

Принятие решений при неопределенности целейИнтегральный критерийМетод НэшаМетод контрольных показателейПростейший методВведение метрики в пространстве целевых функцийСверткаMAUT

Слайд 24Интегральный критерий
x (f1(х), f2(х), …, fn (х))

F(x)
Его роль – поставить в соответствие каждой

альтернативе
только одно число

Интегральный критерий x (f1(х), f2(х), …, fn (х)) F(x) Его роль – поставить

Слайд 25Метод арбитражных решений, или метод Нэша
АУТ(

)

F(x)=

Метод арбитражных решений, или метод НэшаАУТ( )F(x)=

Слайд 26Пример
Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}

F(x1)=(2-2)(7-1)=0
F(x2)=(4-2)(4-1)=6
F(x3)=(3-2)(6-1)=5
F(x4)=(7-2)(1-1)=0
F(x5)=(5-2)(3-1)=6
АУТ (2;1)
х2 ~ х5 по

Нэшу

Слайд 27Использование контрольных показателей
{fi*}n, fi (x) ≥

fi*,

Использование контрольных показателей {fi*}n, fi (x) ≥ fi*,

Слайд 28Пример
Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}
Пусть f1=3; f2=2
АУТ (2;1)
F(x2)=min{4/3;

4/2}=4/3
F(x3)=min{3/3; 6/2}=1
F(x5)=min{5/3; 3/2}=3/2

Слайд 29Простейший способ
Ранг, равный 1, присваивается главному критерию

Слайд 30Введение метрики в пространстве целевых функций
УТ(fimax)

Слайд 31Пример
Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}
h(x1)=5
h(x2)=√18,
h(x3)= √17
h(x4)=6
h(x5)= √20

Слайд 32Пример
А: $ 100 млн; 20 мин; 50 тыс. чел;
Б: $

130 млн; 30 мин; 20 тыс чел;
С: $ 200 млн;

60 мин; 5 тыс чел;

А(61;61;1)
Б(43;46;41)
С( 1; 1; 61)
УТ(61;61;61); АУТ (1;1;1)

Нэш

МКП

Метрика

h(A)=60= √3600
h(Б)=
=
H(C)=√7200

0
42*45*40
0

1
41
1

ПримерА: $ 100 млн; 20 мин; 50 тыс. чел;Б: $ 130 млн; 30 мин; 20 тыс чел;С:

Слайд 33Cвертка

здесь x – альтернатива из множества Парето
fi(x) – оценка

альтернативы x по i-му критерию

Слайд 34Свертка
Ci – коэффициенты относительной важности критериев

Слайд 35Экспертное оценивание
Пусть rij – ранг, который присвоил
j–ый эксперт

i–му критерию

Чтобы получить числовую оценку, введем

новый коэффициент

Экспертное оценивание Пусть rij – ранг, который присвоил j–ый эксперт i–му критерию Чтобы получить числовую

Слайд 36Экспертное оценивание
Тогда коэффициент значимости i-го критерия с точки

зрения j–го эксперта

Ci

Слайд 37Экспертное оценивание
Пусть gj – компетентность j–го эксперта, тогда
Ci

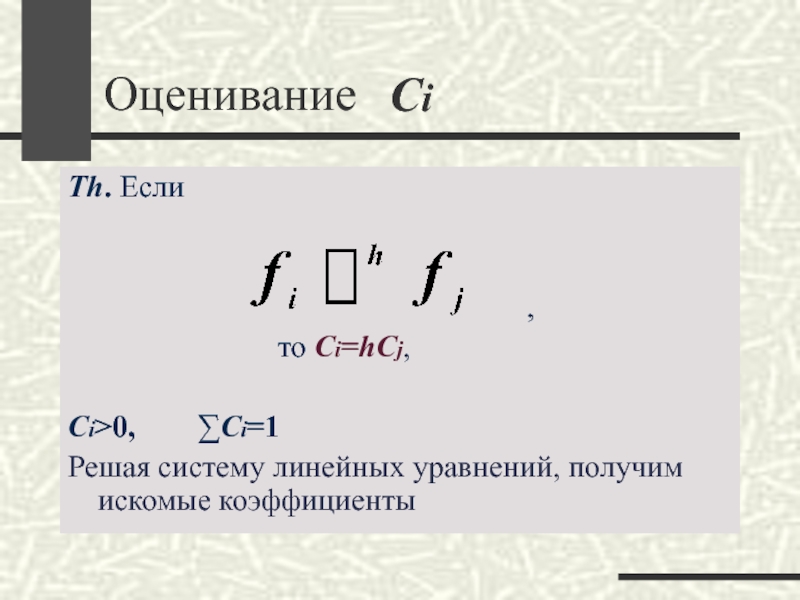
Слайд 38Оценивание
Th. Если

,
то Ci=hCj,

Ci>0, ∑Ci=1
Решая систему линейных уравнений, получим искомые коэффициенты

Слайд 39Пример
,

f2~ f3 ,

C1=3/8; C2=2/8; C3=2/8; C4=1/8

C1=1,5C2;
C2=C3;
C3=2C4;
C1+C2+C3+C4=1;

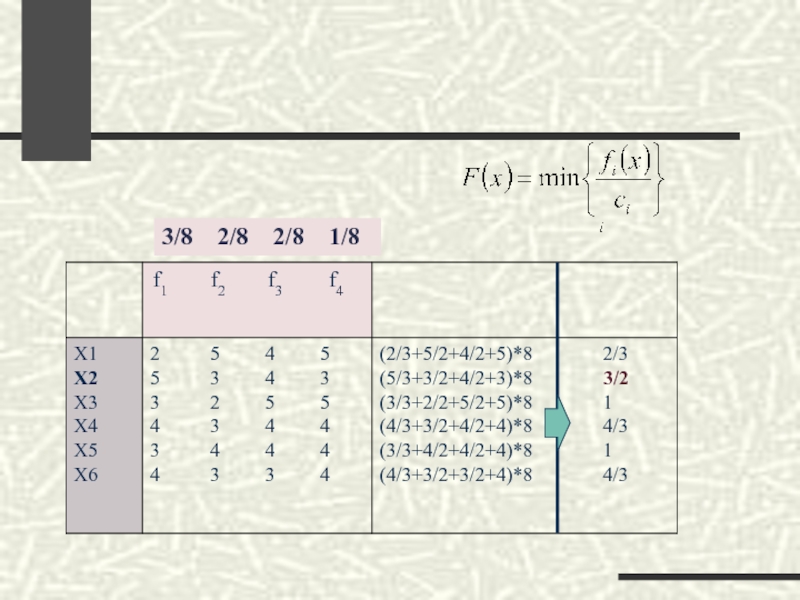
3/8 2/8 2/8 1/8

Слайд 40Использование линейной свертки
Это задачи, связанные с критериями
суммарного ущерба

или прибыли,
дохода,
денежных или временных затрат
по годам планирования

или по этапам
жизненного цикла экономических информационных систем и т. п.,
т.е. там, где допускается, что низкая ценность одной частной характеристики результата компенсируется высокой ценностью другой

Использование линейной свертки Это задачи, связанные с критериями суммарного ущерба или прибыли, дохода, денежных или временных затрат

Слайд 41Квадратичная свертка

Слайд 42Свертка порядка t
Величина t, стоящая в показателе степени,

отражает допустимую степень компенсации малых значений одних критериев большими значениями

других.
Чем больше значение t, тем больше степень возможной компенсации.

Свертка порядка t Величина t, стоящая в показателе степени, отражает допустимую степень компенсации малых значений одних

Слайд 43

недопустима никакая компенсация, и требуется выравнивание значений всех критериев
(равномерное

«подтягивание» значений всех критериев к их наилучшему уровню)

недопустима никакая компенсация, и требуется выравнивание значений всех критериев (равномерное «подтягивание» значений всех критериев к их наилучшему

Слайд 443/8 2/8 2/8 1/8

Слайд 45 t→0

- мультипликативная функция
требуется обеспечение

примерно одинаковых уровней значений отдельных частных критериев

Слайд 46

В задачах планирования ударов «по узкому месту» допустима
компенсация увеличения

одного из критериев сколь угодно большим уменьшением остальных

В задачах планирования ударов «по узкому месту» допустима компенсация увеличения одного из критериев сколь угодно большим уменьшением

Слайд 473/8 2/8 2/8 1/8

Слайд 48Свертка
Используя в качестве интегрального критерия свертку, выбирают в

качестве лучшей ту альтернативу, для которой F(x) имеет максимальное значение

Свертка Используя в качестве интегрального критерия свертку, выбирают в качестве лучшей ту альтернативу, для которой F(x)

Слайд 49Multi-Attribute Utility Theory (MAUT)
Используется при возможном структурировании системы целей, представлении

ее в виде иерархии.
Идея – оценить полезность каждой альтернативы с

точки зрения достижения глобальной цели

Multi-Attribute Utility Theory (MAUT)Используется при возможном структурировании системы целей, представлении ее в виде иерархии.Идея – оценить полезность

Слайд 50Алгоритм MAUT
Оценивается частичная полезность каждой альтернативы по отношению к соответствующему

критерию
Оцениваются коэффициенты относительной важности критериев
Оценивается общая полезность каждой альтернативы по

отношению к главной цели
Лучшей будет та альтернатива, общая полезность которой больше.

Алгоритм MAUTОценивается частичная полезность каждой альтернативы по отношению к соответствующему критериюОцениваются коэффициенты относительной важности критериевОценивается общая полезность

Слайд 51Пример: «Выбор местоположения предприятия»
Местоположение

ЗУ
Местоположение
П
МРиТ
ВГ
РЗУ
ЦЗУ
РО
ПП
КР
ТИ
ТЭФ
ППс
ПБУ
МС
СНД
0.2
0.35
0.25
0.2
0.3
0.5
0.2
0.6
0.4
0.4
0.2
0.25
0.15
0.6
0.4
А, Б, С

Пример: «Выбор местоположения предприятия»МестоположениеЗУМестоположениеПМРиТВГРЗУЦЗУРОППКРТИТЭФППсПБУМССНД0.20.350.250.20.30.50.20.60.40.40.20.250.150.60.4А, Б, С

Слайд 52Оценка частичной полезности альтернатив по критерию

РЗУ, тыс. кв. м:
А –

60
Б – 42.5
С - 35
35
60
1
0.8
0.6
0.4
0.2
А(1), Б(0.2), С(0)
=>
РЗУА=10.30.2=0.06
РЗУБ=0.20.30.2=0.012
РЗУС=0

Оценка частичной полезности альтернатив по критериюРЗУ, тыс. кв. м:А – 60Б – 42.5С - 3535 6010.80.60.40.2А(1), Б(0.2),

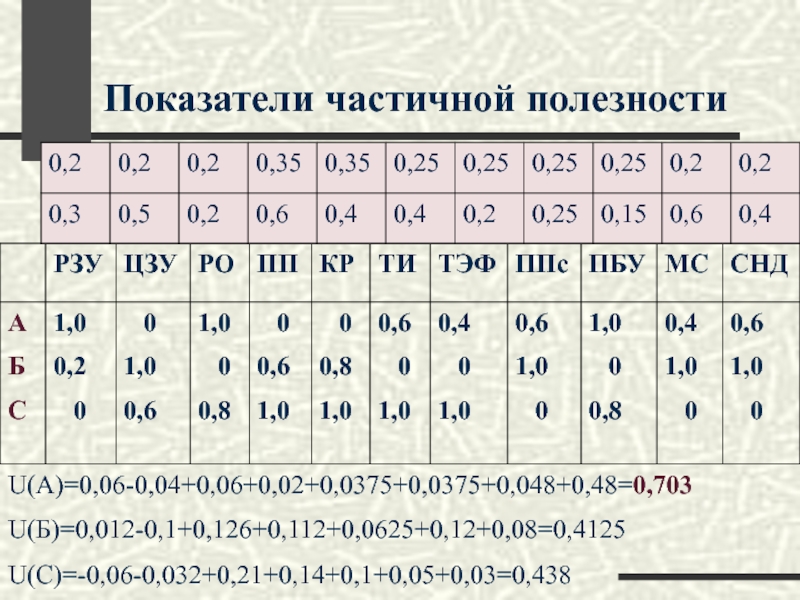
Слайд 53Показатели частичной полезности
U(A)=0,06-0,04+0,06+0,02+0,0375+0,0375+0,048+0,48=0,703
U(Б)=0,012-0,1+0,126+0,112+0,0625+0,12+0,08=0,4125
U(C)=-0,06-0,032+0,21+0,14+0,1+0,05+0,03=0,438

Показатели частичной полезностиU(A)=0,06-0,04+0,06+0,02+0,0375+0,0375+0,048+0,48=0,703U(Б)=0,012-0,1+0,126+0,112+0,0625+0,12+0,08=0,4125U(C)=-0,06-0,032+0,21+0,14+0,1+0,05+0,03=0,438

Слайд 54Применение
«+»: Относительно простой способ нахождения решения в МКЗ путем системного

структурирования и легкой интерпретации результатов - позволяет оценивать любые (в

том числе и вновь появляющиеся альтернативы)
«-»:
предполагается, что человек может дать точные количественные оценки;
сложно определять веса критериев,
функции преобразования

Применение«+»: Относительно простой способ нахождения решения в МКЗ путем системного структурирования и легкой интерпретации результатов - позволяет

Слайд 55

Скачать презентацию

Разделы презентаций

Преодоление неопределенностей целей

Содержание

Слайды и текст этой презентации

Слайд 1Принятие решений при неопределенности целей1 Постановка многокритериальной задачи2 Множество Парето.

Поле полезности решений. Конус предпочтения

Слайд 2Пример «Строительство аэропорта»КритерииСтоимость строительстваРасстояние от городаМинимальное шумовое воздействие

Слайд 3Пример (альтернативы)А: $ 100 млн; 20 мин; 50 тыс. чел;Б:

$ 130 млн; 30 мин; 20 тыс чел;С: $ 200

Слайд 4МКЗ(Ω, {fi}n, {⎬,~}),где {fi}n - n целевых функций fi, каждая

из которых сформулирована в виде fi(х)→max

Слайд 5МКЗ 1. Цели взаимно нейтральны 2. Цели кооперируются3. Цели конкурируютЦели

могут находиться друг с другом в различных отношениях:

Слайд 6 Цели нейтральны

Слайд 7Алгоритм решения МКЗуменьшить исходное множество альтернатив, убрав заведомо худшиесвести задачу

к однокритериальной путем введения интегрального критерия

Слайд 8МКЗx1 (f1(x1), f2(x1), …,

fn(x1)) x2 (f1(x2), f2(x2),

Слайд 9Принцип ПаретоПусть x1 и x2 – альтернативы.

Если для i fi(x1) ≥

Слайд 10Множество ПаретоОставшиеся альтернативы образуют множество Парето - множество

неулучшаемых альтернатив, или множество несравнимых альтернатив,

Слайд 11Множество Паретоили таких, улучшение которых по одним критериям приводит к

их ухудшению по другимВозможные решения следует искать лишь среди неулучшаемых

Слайд 12Критериальное пространство В критериальном пространстве альтернативы

заданы точками, проекции которых

Слайд 13Конус предпочтения

Слайд 14Поле полезности

Слайд 15Способы задания альтернативкоординатный (альтернативы заданы своими координатами в

критериальном пространстве)графический (альтернативы образуют непрерывное множество и изображены точками

Слайд 16Множество ПаретоХ1(2;7)Х2(4;4)Х3(3;6)Х4(7;1) Х5(5;3)Х6(6;0)Х7(4;3)═>

Слайд 17Множество ПаретоР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}АУТ (2;1)УТ (7;7)7127f1f2АУТУТ

Слайд 18Множество Парето

Слайд 19Множество Парето

Слайд 20Множество ПаретоВсе альтернативы из множества Парето являются решением многокритериальной задачи

в смысле этого принципа, т.е. являются паретооптимальными Основным недостатком таких

Слайд 21Перевод в однородную шкалуfi*(x) - оценка альтернативы x по i-му

критерию в «родной» шкале fimax и fimin - максимальное

Слайд 22Перевод в однородную шкалуА: $ 100 млн; 20

мин; 50 тыс. чел;Б: $ 130 млн;

Слайд 23Принятие решений при неопределенности целейИнтегральный критерийМетод НэшаМетод контрольных показателейПростейший методВведение

метрики в пространстве целевых функцийСверткаMAUT

Слайд 24Интегральный критерий x (f1(х), f2(х), …, fn (х))

F(x) Его роль – поставить в соответствие каждой

Слайд 25Метод арбитражных решений, или метод НэшаАУТ(

)F(x)=

Слайд 26ПримерР {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)}F(x1)=(2-2)(7-1)=0F(x2)=(4-2)(4-1)=6F(x3)=(3-2)(6-1)=5F(x4)=(7-2)(1-1)=0F(x5)=(5-2)(3-1)=6АУТ (2;1)х2 ~ х5 по