Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы стереометрии
Содержание
- 1. Аксиомы стереометрии
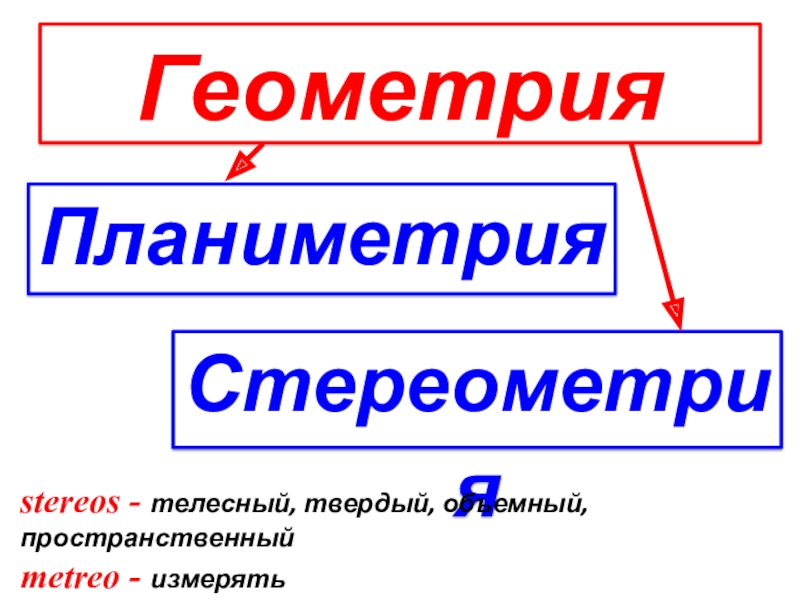
- 2. ГеометрияПланиметрияСтереометрия stereos - телесный, твердый, объемный, пространственныйmetreo - измерять
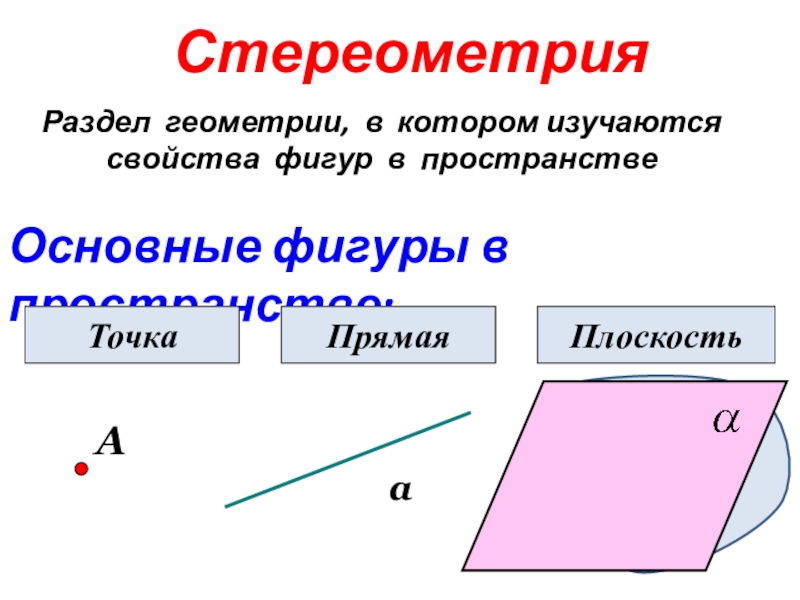
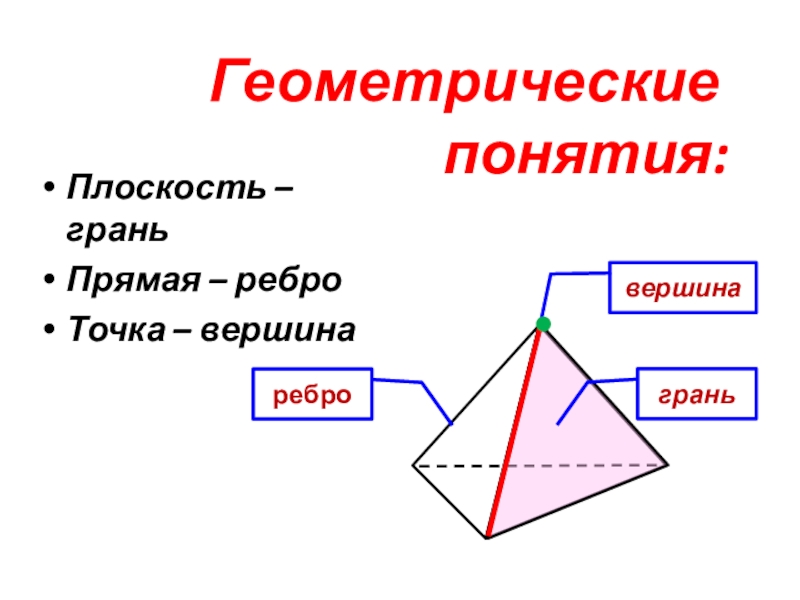
- 3. СтереометрияРаздел геометрии, в котором изучаются свойства фигур в пространствеОсновные фигуры в пространстве:АТочкааПрямаяПлоскость
- 4. Обозначение основных фигур в пространстве:точкапрямаяплоскостьA, B, C, …a, b, c, …илиAВ, BС, CD, …
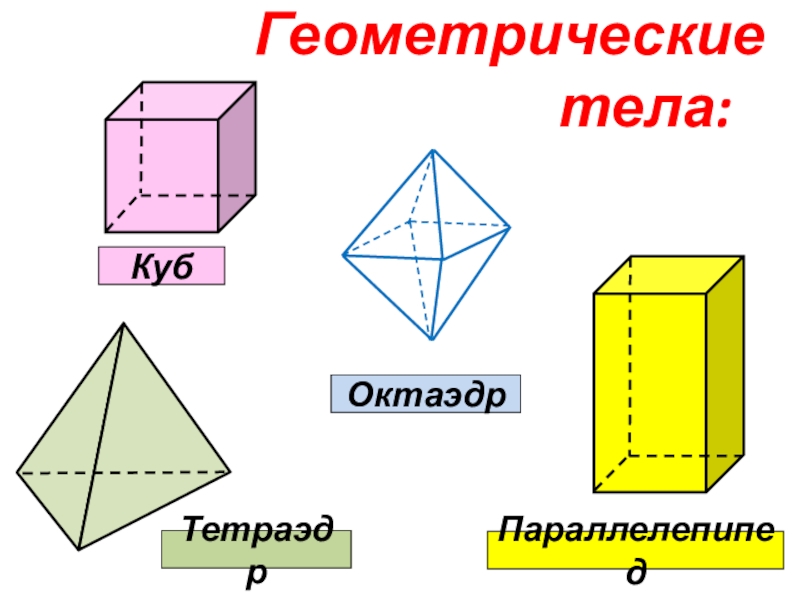
- 5. Геометрические тела:КубПараллелепипедТетраэдрОктаэдр
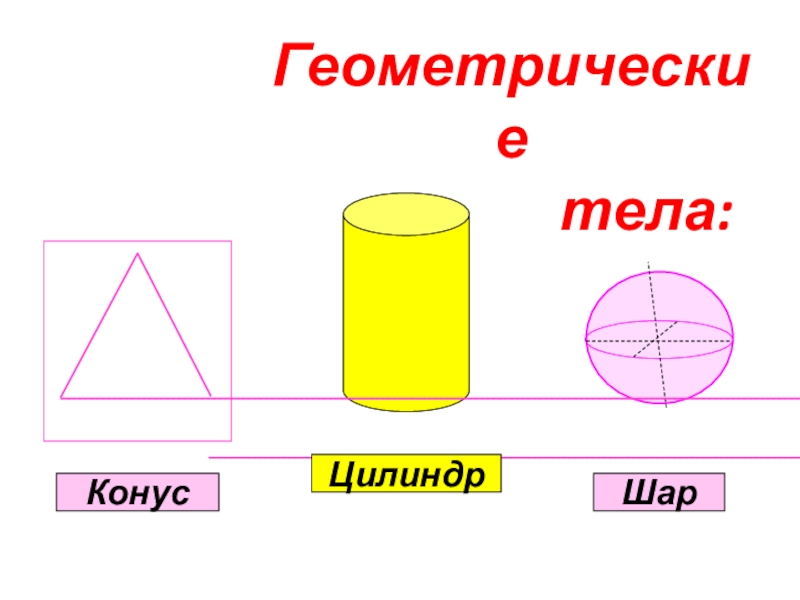
- 6. Геометрические тела:ЦилиндрКонусШар
- 7. Геометрические
- 8. Аксиома(от греч. axíõma – принятие положения)- исходное
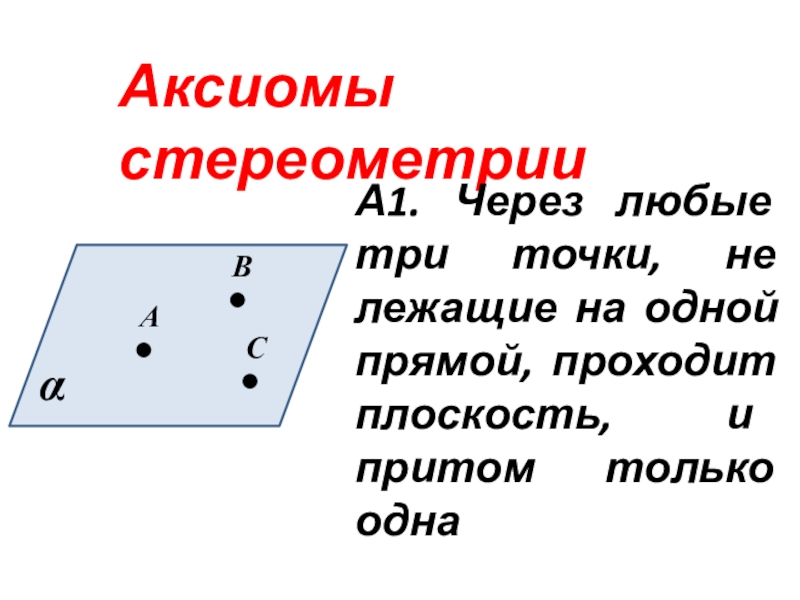
- 9. Аксиомы стереометрииА1. Через любые три точки, не
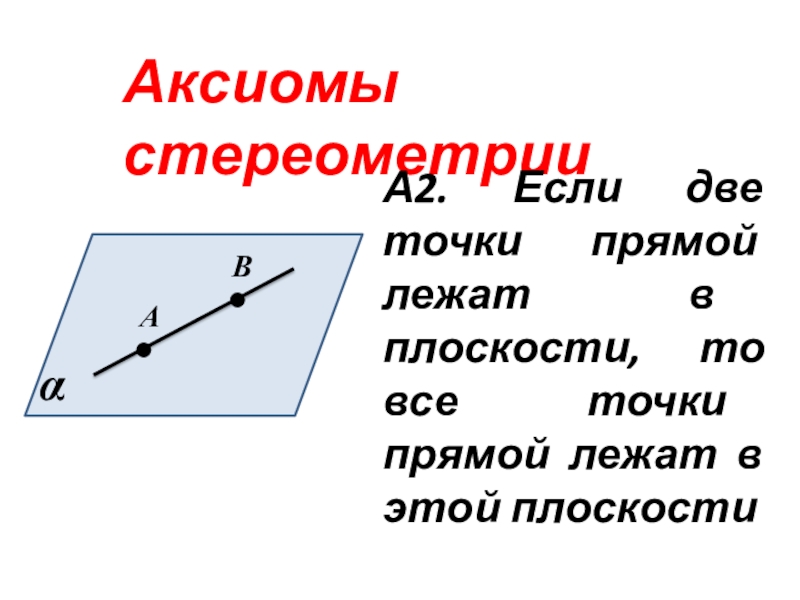
- 10. Аксиомы стереометрииА2. Если две точки прямой лежат
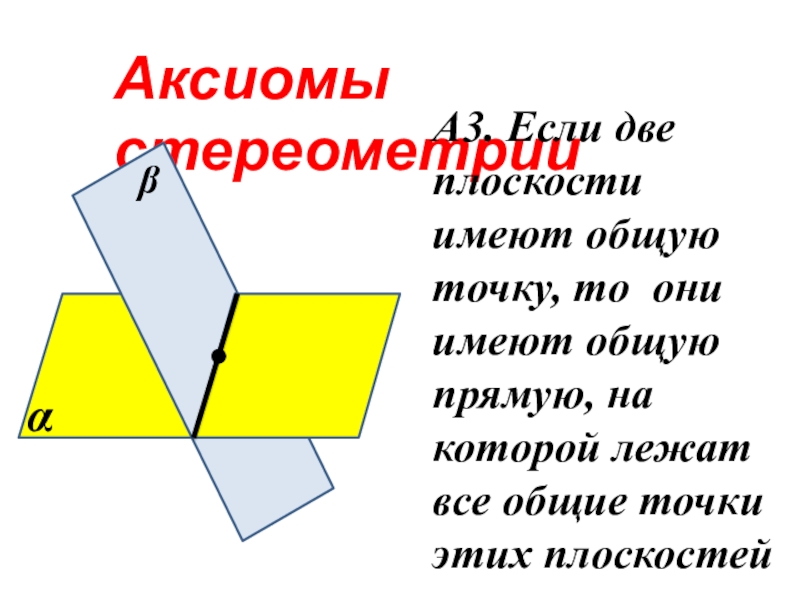
- 11. Аксиомы стереометрииА3. Если две плоскости имеют общую
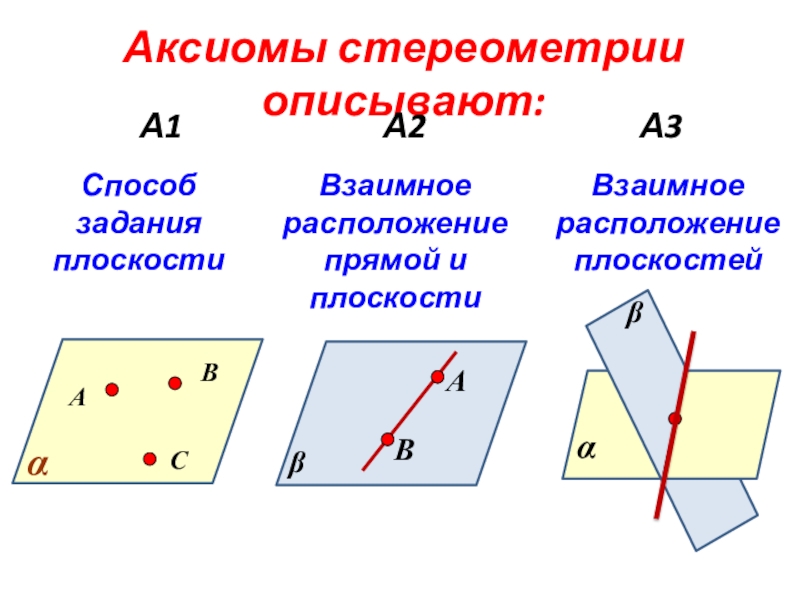
- 12. Аксиомы стереометрии описывают:А1А2 А3 АВССпособ задания плоскостиАВВзаимное расположение прямой и плоскостиВзаимное расположение плоскостей
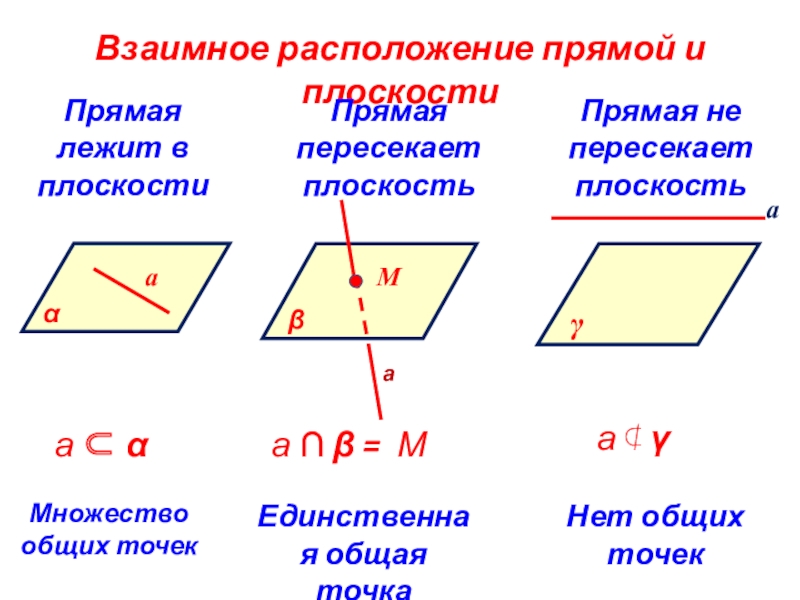
- 13. Взаимное расположение прямой и плоскостиПрямая лежит в
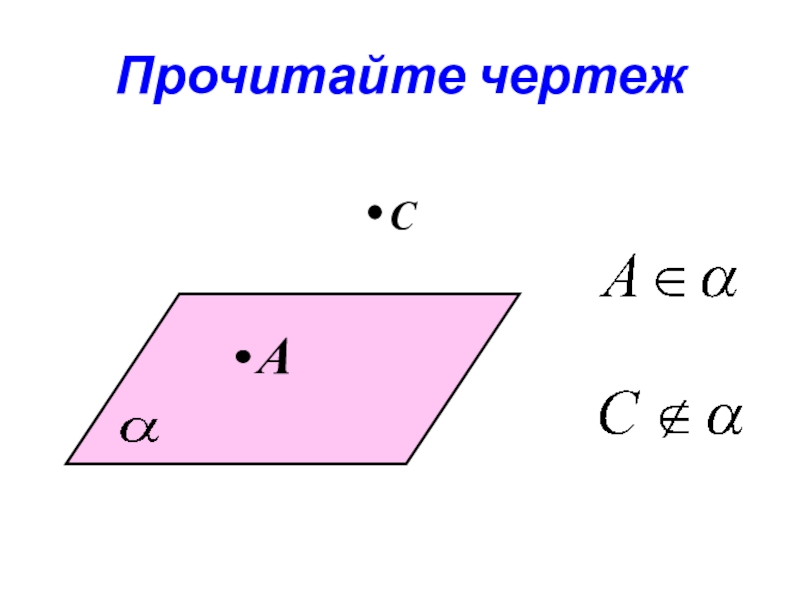
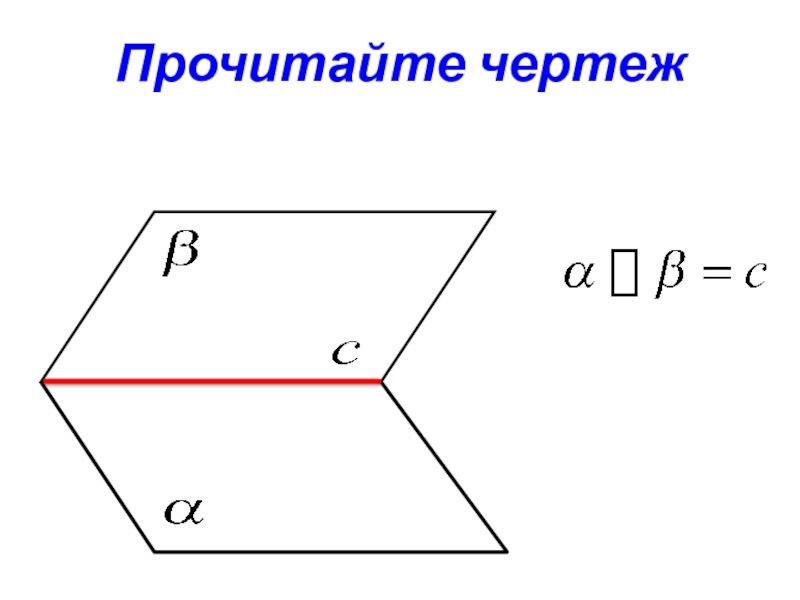
- 14. Прочитайте чертежAС
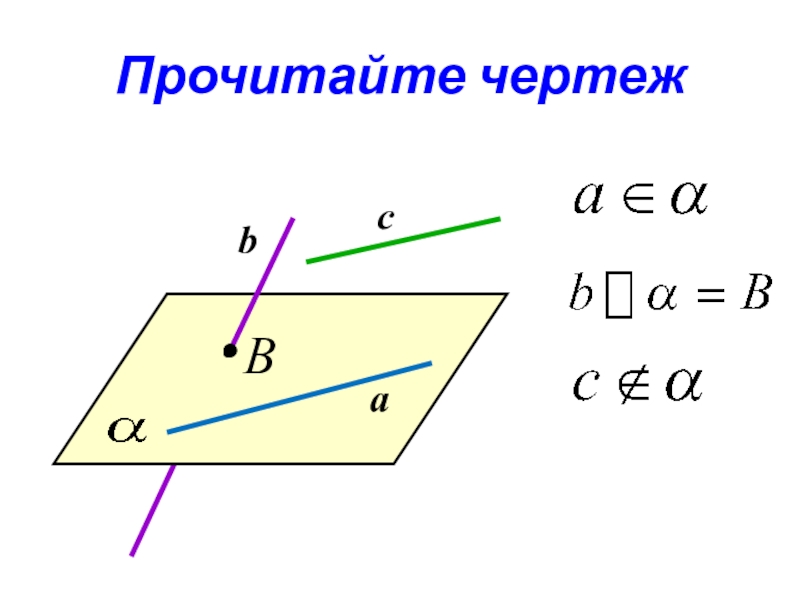
- 15. Прочитайте чертежBcba
- 16. Прочитайте чертеж
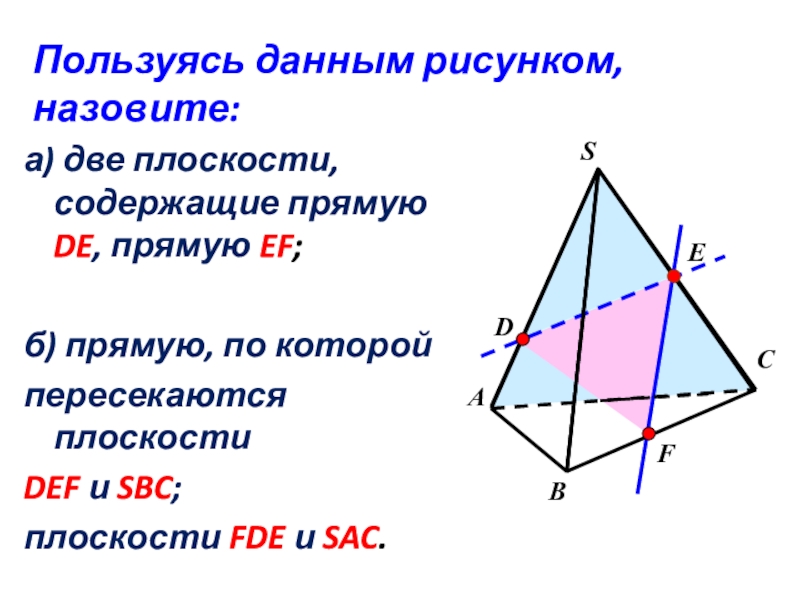
- 17. а) две плоскости, содержащие прямую DE, прямую
- 18. Домашнее задание:Выучить аксиомы2) Введение, п. 2,3,стр. 4 – 63) № 2,15
- 19. Скачать презентанцию
ГеометрияПланиметрияСтереометрия stereos - телесный, твердый, объемный, пространственныйmetreo - измерять
Слайды и текст этой презентации
Слайд 1Аксиомы стереометрии
Геометрия. Урок № 1
10 класс
Евклид
Если теорему так и не
смогли доказать, она становится аксиомой
Слайд 2Геометрия
Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять
Слайд 3Стереометрия
Раздел геометрии, в котором изучаются свойства фигур в пространстве
Основные фигуры
в пространстве:
А
Точка
а
Прямая
Плоскость
Слайд 4Обозначение основных
фигур в пространстве:
точка
прямая
плоскость
A, B, C, …
a, b, c,
…
или
AВ, BС, CD, …
Слайд 8Аксиома
(от греч. axíõma – принятие положения)
- исходное положение научной теории,
принимаемое без доказательства -
"Так называемые аксиомы
математики
- это те немногие
мыслительные определения,
которые необходимы в математике
в качестве исходного пункта"Ф. Энгельс
Слайд 9Аксиомы стереометрии
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна
А
В
С
Слайд 10Аксиомы стереометрии
А2. Если две точки прямой лежат в плоскости, то
все точки прямой лежат в этой плоскости
А
В
Слайд 11Аксиомы стереометрии
А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие точки этих
плоскостей
Слайд 12Аксиомы стереометрии описывают:
А1
А2
А3
А
В
С
Способ задания плоскости
А
В
Взаимное расположение прямой и
плоскости
Взаимное расположение плоскостей
Слайд 13Взаимное расположение прямой и плоскости
Прямая лежит в плоскости
Прямая пересекает плоскость
Прямая
не пересекает плоскость
Множество общих точек
Единственная общая точка
Нет общих точек
а
а
М
g
а
а
а ∩ = М
а ⊄
Слайд 17а) две плоскости, содержащие прямую DE, прямую EF;
б) прямую, по
которой
пересекаются плоскости
DEF и SBC;
плоскости FDE и SAC.
Пользуясь данным рисунком,
назовите:
