Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра высказываний.
Содержание
- 1. Алгебра высказываний.
- 2. Список литературы 1.Шишмарев Ю.Е.
- 3. Алгебра высказываний1. Основные понятия. Логические операцииПод высказыванием
- 4. Операции над высказываниями. ОтрицаниеОпределение 1Высказывание "неверно, что
- 5. Из высказываний А, В можно образовать высказывание
- 6. Из высказываний А, В можно образовать высказывание
- 7. Из высказываний А, В можно образовать следующее
- 8. Эквивалентность задается таблицей истинности: Эквивалентность
- 9. Из высказываний А и В можно образовать
- 10. Задается импликация таблицей истинности: ИмпликацияПримеры1. D="если сегодня
- 11. Сделаем замечания, которые могут прояснить суть определения
- 12. Определение 6Переменная А, принимающая два значения – 0
- 13. Определение 2Таблица истинности для высказывания
- 14. Порядок действий1)Однотипные операции выполняются в порядке их
- 15. Примеры1)Избавиться от лишних скобокОтвет 2)Расставить порядок действий1234567
- 16. ПримерФормализовать высказывание:F=«Хлеба уцелеют тогда и только тогда,
- 17. Пример Построить таблицу истинности для высказывания
- 18. 2. Равносильные высказывания Определение 1Высказывания F(A1,A2,…,An) и
- 19. Примеры Доказательство
- 20. Основные логические тождестваИдемпотентные законы: Коммутативные законы: Ассоциативные законы: 1)2)3)4)5)6)7)8)
- 21. Законы Моргана: Закон двойного отрицания: Закон противоречия: Закон исключенного третьего: 9)10)11)12)13)14)15)Дистрибутивные законы: Без названия:16)17)
- 22. Законы поглощения: ДоказательствоДоказательство16)17)18)19)
- 23. Тождества, содержащие константы:
- 24. Определение 1Конъюнкция логических переменных или их отрицаний
- 25. Примеры
- 26. Теорема Любое высказывание приводимо к ДНФ.Схема приведения
- 27. ПримерПривести высказывание к ДНФ
- 28. 4.Построение высказываний по таблице истинности. Совершенные дизъюнктивные
- 29. Определение 2Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие ее элементарные конъюнкции являются полными.ПримерыСДНФ
- 30. Приведение высказывания к СДНФТеорема
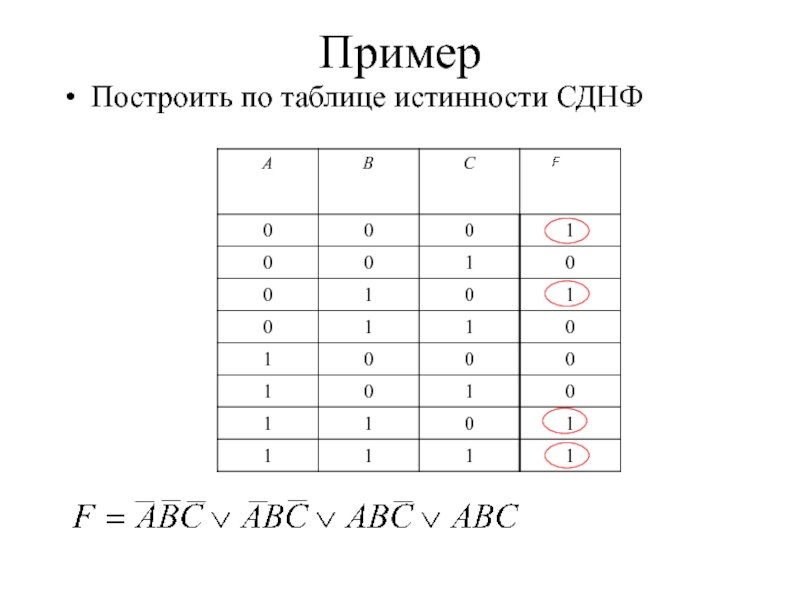
- 31. ПримерПостроить по таблице истинности СДНФ
- 32. Задача «Вернувшись домой, Мегрэ позвонил на набережную
- 33. Решение задачиПустьP=« Франсуа был пьян»L=«Франсуа лжет»I=«Этьен убийца»U=«Убийство
- 34. Приложения алгебры высказываний. Исследование переключательных
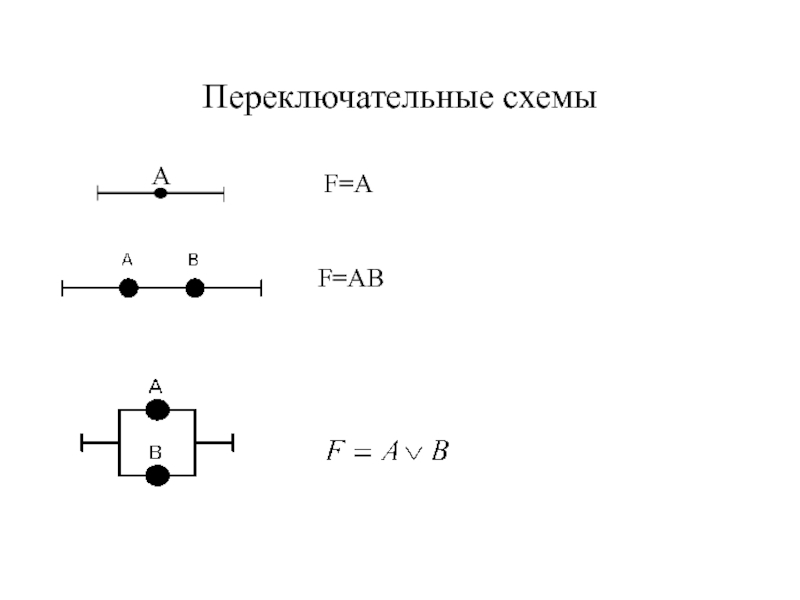
- 35. Переключательные схемы AF=AF=AB
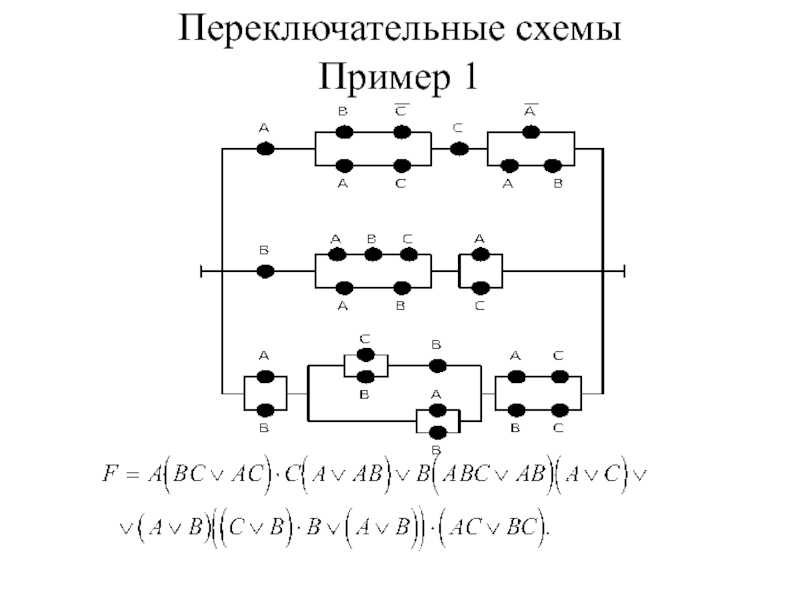
- 36. Переключательные схемы Пример 1
- 37. Переключательные схемы. Пример 1
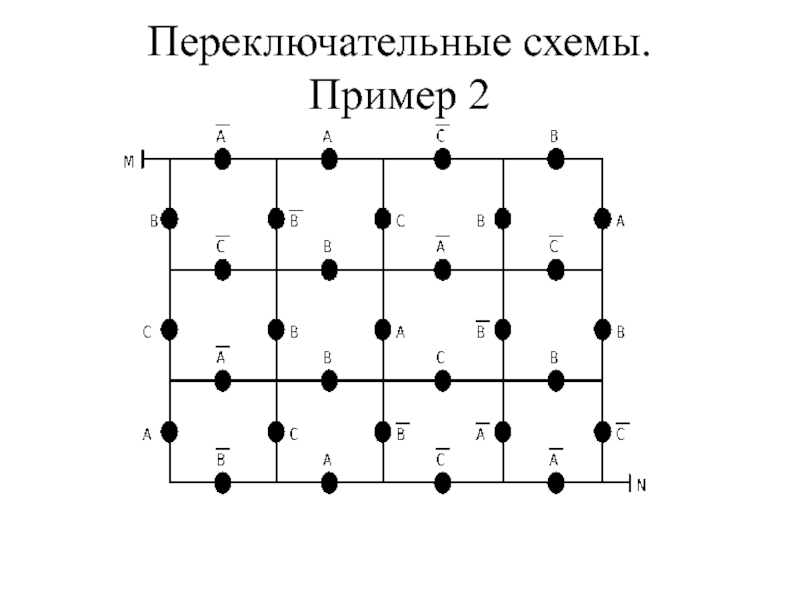
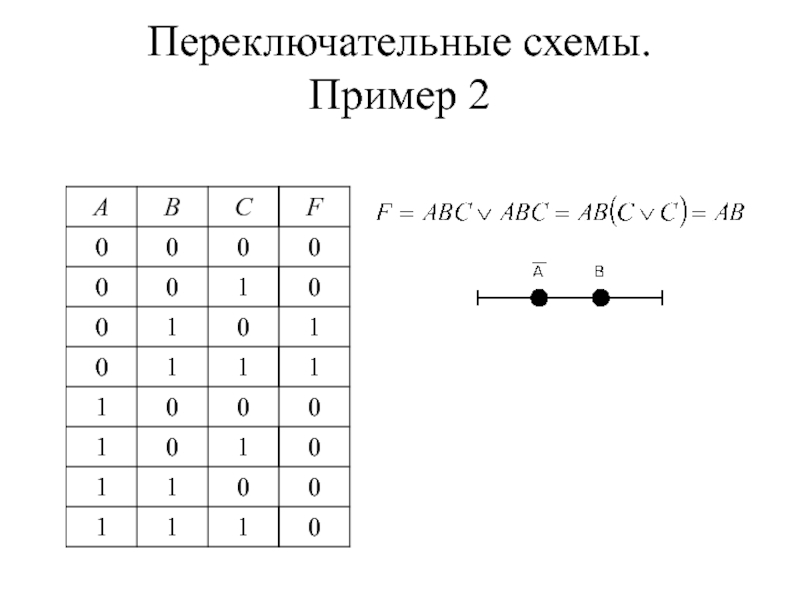
- 38. Переключательные схемы. Пример 2
- 39. Переключательные схемы. Пример 2
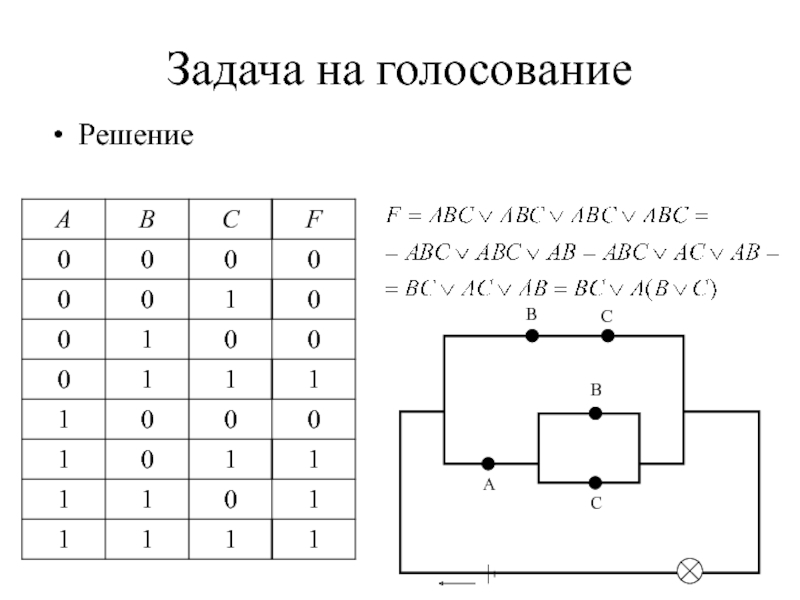
- 40. Задача на голосование Построить контактную схему для
- 41. Задача на голосованиеРешение
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Алгебра высказываний
1. Основные понятия. Логические операции
Под высказыванием мы понимаем предложение
русского языка, о котором можно сказать, истинно оно или ложно.
Высказывания мы будем обозначать заглавными буквами латинского алфавита, возможно с индексами:
Если высказывание А истинно, мы будем писать А=1; если высказывание А ложно, мы будем писать А=0.
Примеры
1. А=«два умножить на два равно семи»
2. В=«два плюс два равно 4»
3. С=«если сентябрь – весенний месяц, то 5*5=25»
4.D=«число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3»
5.E=«если после четверга следует пятница, то в году 13 месяцев»
A=0
B=1
C=?
D=1
E=?
Слайд 4Операции над высказываниями.
Отрицание
Определение 1
Высказывание "неверно, что А" называется отрицанием А
и обозначается
Задается действие отрицания с помощью таблицы истинности:
Слайд 5Из высказываний А, В можно образовать высказывание "А и В".
Например, "2*2=4 и 5+3=9"
Определение 2
Высказывание "А и В" называется
конъюнкцией (или логическим умножением) высказываний А и В.Конъюнкция имеет много обозначений:
Конъюнкция задается с помощью таблицы истинности:
Конъюнкция
Слайд 6Из высказываний А, В можно образовать высказывание "А или В".
Например, "2*2=4 или 5+3=9".
Определение 3
Высказывание "А или В" называется дизъюнкцией
(или логическим сложением) высказываний А и Ви обозначается A v B
Дизъюнкция задается с помощью таблицы истинности:
Дизъюнкция
Слайд 7Из высказываний А, В можно образовать следующее высказывание:
"А тогда
и только тогда, когда В".
Например, треугольник является равносторонним тогда и
только тогда, когда все его углы равны между собой.Синонимами служат фразы:
"А в том и только в том случае, когда В",
"А необходимо и достаточно для того, чтобы выполнялось В",
"А равносильно В",
"А эквивалентно B".
Определение 4
Высказывание "А равносильно В" называется эквивалентностью высказываний А и В и обозначается:
Эквивалентность
Слайд 9Из высказываний А и В можно образовать высказывание "если А,
то В".
Например, если две прямые параллельны третьей, то они параллельны
между собой.Синонимами служат следующие фразы:
"из А следует В",
"В является следствием А",
"А влечет В",
"А достаточное условие для В",
"В необходимое условие для А" и т.п.
Определение 5
Высказывание "если А, то В" называется импликацией высказываний А и В
и обозначается:
В этой ситуации высказывание А называется посылкой, а В – заключением.
Импликация
Слайд 10Задается импликация таблицей истинности:
Импликация
Примеры
1. D="если сегодня среда, то завтра
будет четверг"
D=1
2. Y="если после четверга следует пятница, то
после пятницы следует воскресенье“Y=0
3. Х="если два плюс два равно пяти, то три плюс два равно десяти“
X=1
4. Z="если 1+1=3, то после пятницы следует суббота“
Z=1
Слайд 11Сделаем замечания, которые могут прояснить суть определения таблицы истинности для
импликации и, возможно, помогут получше ее запомнить:
1)
если посылка ложна, то импликация всегда истинна, независимо от заключения, то есть 2) если заключение истинно, то импликация также истинна, независимо от посылки, то есть
Или обобщающая фраза: “из истины ложь не следует”
Импликация
Слайд 12Определение 6
Переменная А, принимающая два значения – 0 или 1, называется
логической (или булевой) переменной.
Обозначаться логические переменные будут заглавными латинскими буквами
с индексами или без них: Слайд 13Определение 2
Таблица истинности для высказывания
имеет вид
Если высказывание F построено из логических переменных
, то будем обозначать это высказывание:
Теорема
Наборов длины n из 0 и 1 существует
Слайд 14Порядок действий
1)Однотипные операции выполняются в порядке их следования.
Например,
2) Отрицание
подразумевает скобки.
3) Конъюнкция связывает сильнее, чем дизъюнкция.
Например,
4) Дизъюнкция связывает
сильнее, чем импликация.Например,
5) Импликация связывает сильнее, чем эквивалентность.
Например,
Слайд 16Пример
Формализовать высказывание:
F=«Хлеба уцелеют тогда и только тогда, когда будут вырыты
ирригационные канавы; если хлеба не уцелеют, то фермеры обанкротятся и
оставят фермы.»Решение
Пусть
А=«хлеба уцелеют»
B=«будут вырыты ирригационные канавы»
С=«фермеры обанкротятся»
D=«фермеры оставят фермы».
Тогда
Слайд 182. Равносильные высказывания
Определение 1
Высказывания F(A1,A2,…,An) и G(A1,A2,…,An) называются равносильными
(или просто равными), если для любого набора
имеет место равенство:
Обозначим
Другими словами, два высказывания равны, если у них совпадают таблицы истинности.
Слайд 20Основные логические тождества
Идемпотентные законы:
Коммутативные законы:
Ассоциативные законы:
1)
2)
3)
4)
5)
6)
7)
8)
Слайд 21Законы Моргана:
Закон двойного отрицания:
Закон противоречия:
Закон исключенного третьего:
9)
10)
11)
12)
13)
14)
15)
Дистрибутивные законы:
Без названия:
16)
17)
Слайд 24Определение 1
Конъюнкция логических переменных или их отрицаний называется элементарной конъюнкцией.
Пример
Определение
2
Высказывание называется дизъюнктивной нормальной формой (ДНФ), если оно представляет собою
дизъюнкцию элементарных конъюнкций. Общий вид ДНФ:
3. Дизъюнктивные нормальные формы (ДНФ)
Слайд 26Теорема
Любое высказывание приводимо к ДНФ.
Схема приведения высказывания к ДНФ
Избавиться
от импликации и эквивалентности, используя законы
16), 17)
2) Донести отрицания до
переменных, используя законы Моргана.3) Раскрыть скобки, используя дистрибутивные законы.
4) Упростить полученное высказывание.
Слайд 284.Построение высказываний по таблице истинности. Совершенные дизъюнктивные нормальные формы (СДНФ)
Определение
1
Пусть
– некоторое множество логических переменных. Элементарная конъюнкция, в которую входят все логические переменные, называется полной элементарной конъюнкцией относительно множества X .Пример
Слайд 29Определение 2
Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие
ее элементарные конъюнкции являются полными.
Примеры
СДНФ
Слайд 30Приведение высказывания к СДНФ
Теорема
Высказывание, не являющееся
тождественно ложным, приводимо к СДНФ. Правило приведения высказывания к СДНФ
СДНФ содержит столько полных элементарных конъюнкций, сколько единиц в последнем столбце таблице истинности.
Вид каждой полной элементарной определяется соответствующим набором значений переменных, а именно, если переменная принимает значение 0, то над ней в полной элементарной конъюнкцией ставится отрицание, иначе – отрицание не ставится.
Слайд 32Задача
«Вернувшись домой, Мегрэ позвонил на набережную Орфевр.
- Говорит Мегрэ.
Есть новости?
- Да, шеф. Поступили сообщения от инспекторов.
Торранс установил,
что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет.Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи.
Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет.
Затем звонила …
- Все. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.»
Что знал Мегрэ?
Слайд 33Решение задачи
Пусть
P=« Франсуа был пьян»
L=«Франсуа лжет»
I=«Этьен убийца»
U=«Убийство произошло после полуночи»
Тогда
получим высказывание
Так как
, то Этьен - убийцаСлайд 34 Приложения алгебры высказываний.
Исследование переключательных схем
Переключательная схема — это схематическое
изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников,
а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.Каждый переключатель X имеет только два состояния: замкнутое (X=1) и разомкнутое(X=0). .