Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмы обучения без учителя
Содержание
- 1. Алгоритмы обучения без учителя
- 2. Алгоритм MAXMINРассмотрим алгоритм, более эффективный по сравнению
- 3. Алгоритм MAXMINНа первом этапе алгоритма все объекты
- 4. В этом алгоритме пороговое расстояние не является
- 5. АлгоритмВыбрать точку-прототип первого класса (например, объект Х1
- 6. Алгоритм
- 7. Алгоритм
- 8. Рассмотрим работу алгоритма MAXMIN на примере. Как
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Проблемы алгоритма K-средних:необходимо заранее знать количество кластеров.
- 29. Слайд 29
- 30. Слайд 30
- 31. Нечеткий алгоритм кластеризации с-means С последней проблемой
- 32. Слайд 32
- 33. Алгоритм ISODATA (Iterative Self-Organizing Data Analysis Techniques)
- 34. Это число выступает в качестве рекомендации: в
- 35. Ликвидируются кластеры, в состав которых входит менее
- 36. Решение о расщеплении принимается с учетом размера
- 37. Слайд 37
- 38. Использующиеся в алгоритме ISODATA эвристики помогают не
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
- 56. Задача минимизации количества решающих функций, достаточных для
- 57. Слайд 57
- 58. Слайд 58
- 59. Прямого ответа на этот вопрос можно избежать,
- 60. Эти эталонные объекты являются наиболее типичными представителями
- 61. Слайд 61
- 62. Классы, однако, могут обладать разными свойствами. Простейшим
- 63. Слайд 63
- 64. Слайд 64
- 65. В соответствии с данным решающим правилом просматривается
- 66. Метод ближайшего соседа весьма чувствителен к выбросам,
- 67. Слайд 67
- 68. Слайд 68
- 69. Слайд 69
- 70. Слайд 70
- 71. Слайд 71
- 72. Слайд 72
- 73. Слайд 73
- 74. Слайд 74
- 75. Слайд 75
- 76. Слайд 76
- 77. Слайд 77
- 78. Слайд 78
- 79. Слайд 79
- 80. Слайд 80
- 81. Слайд 81
- 82. Слайд 82
- 83. Слайд 83
- 84. Слайд 84
- 85. Слайд 85
- 86. Скачать презентанцию
Алгоритм MAXMINРассмотрим алгоритм, более эффективный по сравнению с предыдущим и являющийся улучшением порогового алгоритма. Исходными даннымы для работы алгоритма будет, как и раньше, выборка X. Объекты этой выборки следует разделить на
Слайды и текст этой презентации
Слайд 3Алгоритм MAXMIN
На первом этапе алгоритма все объекты разделяются по классам
на основе критерия минимального расстояния от точек-прототипов этих классов (первая
точка-прототип может выбираться произвольо). Затем в каждом классе выбирается объект, наиболее удаленный от своего прототипа. Если он удален от своего прототипа на расстояние, превышающее пороговое, такой объект становится прототипом нового класса.
Слайд 4В этом алгоритме пороговое расстояние не является фиксированным, а определяется
на основе среднего расстояния между всеми точками-прототипами, то есть корректируется
в процессе работы алгоритма. Если в ходе распределения объектов выборки X по классам были созданы новые прототипы, процесс распределения повторяется. Таким образом, в алгоритме MAXMIN окончательным считается разбиение, для которого в каждом классе расстояние от точки-прототипа до всех объектов этого класса не превышает финального значения порога Т.
Слайд 5Алгоритм
Выбрать точку-прототип первого класса (например, объект Х1 из обучающей выборки).
Количество классов К положить равным 1. Обозначить точку-прототип Z1.
Определить наиболее
удаленный от Z1 объект Xf по условиюD(Z1,Xf) = max D(Z1, Xi),
где D(Z1,Xf) - расстояние между Z1 и Xf, вычисленное одним из возможных способов. Объявить Xf прототипом второго класса. Обозначить Xf как Z2. Число классов К = К + 1.
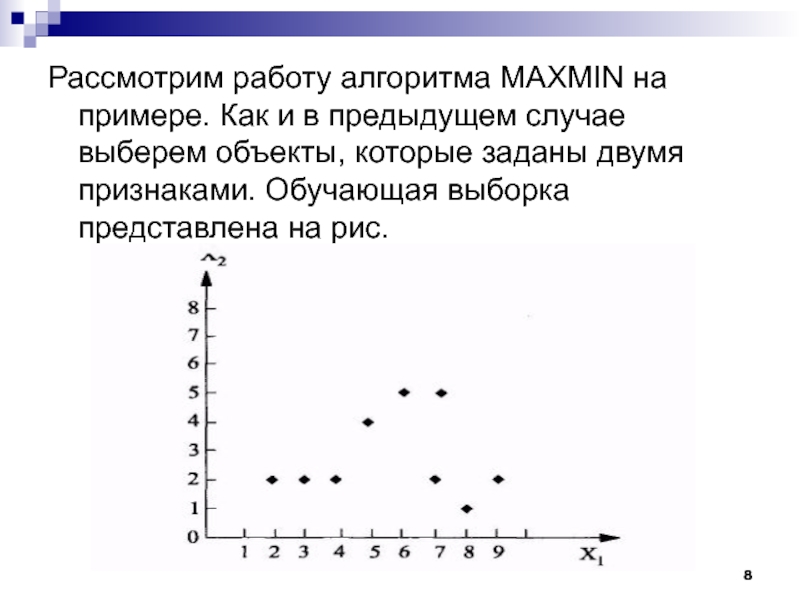
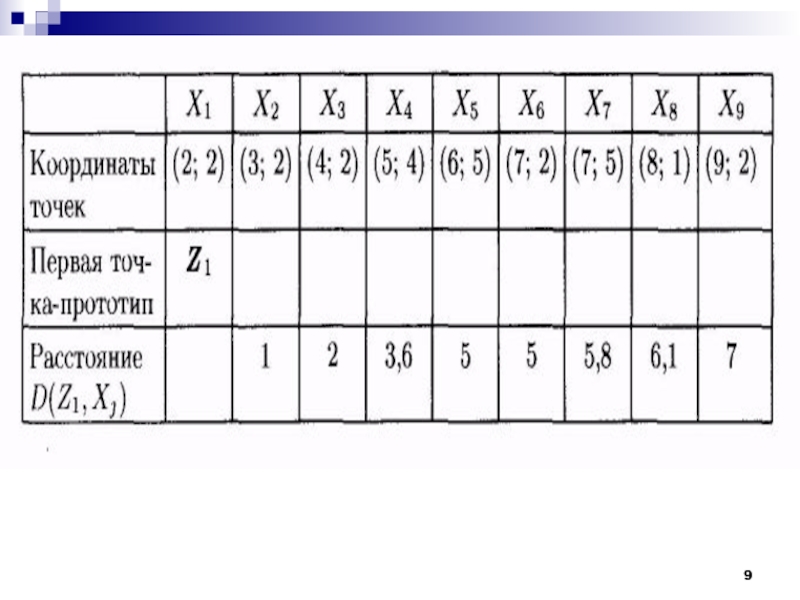
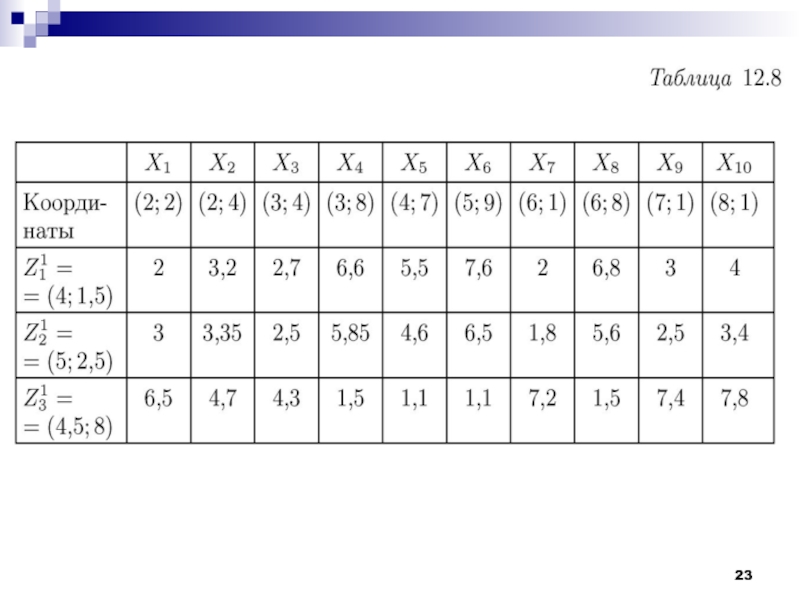
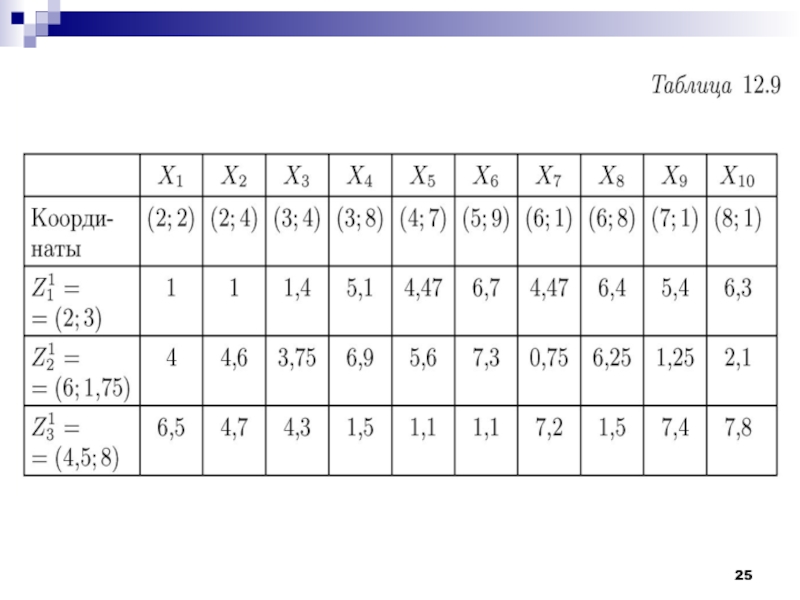
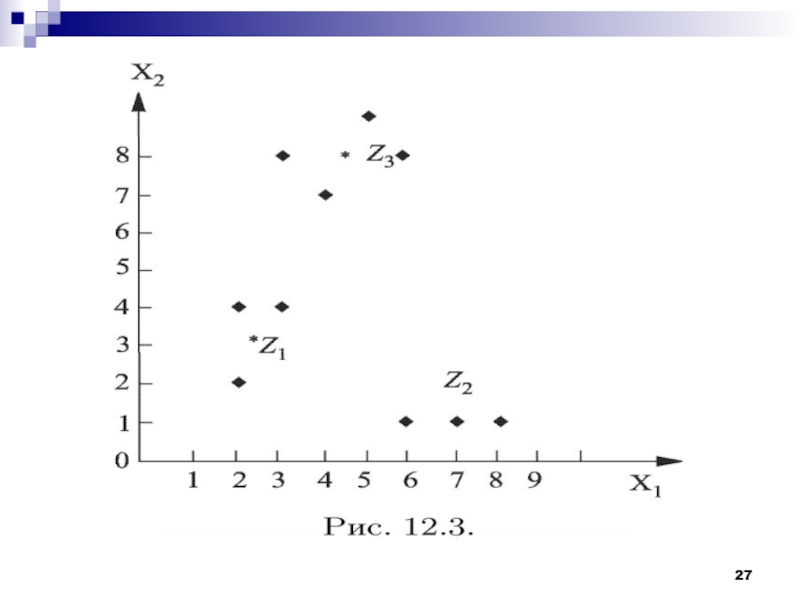
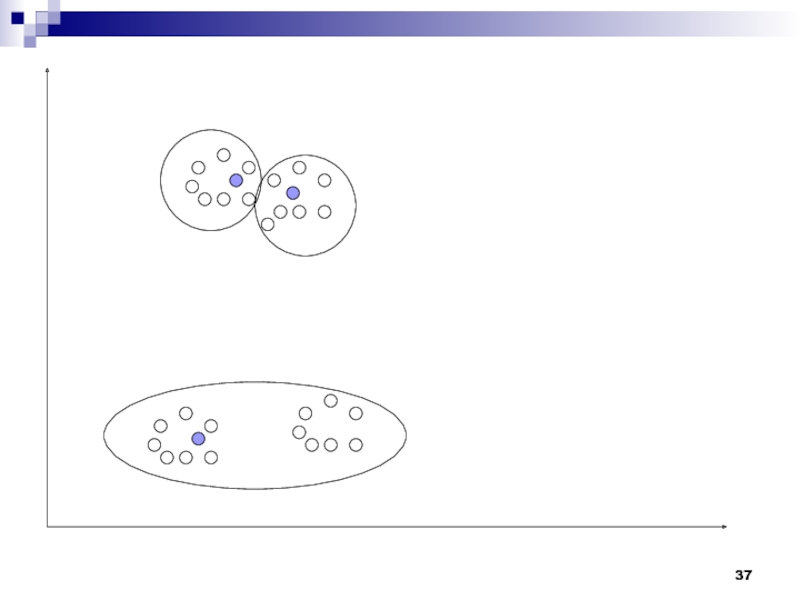
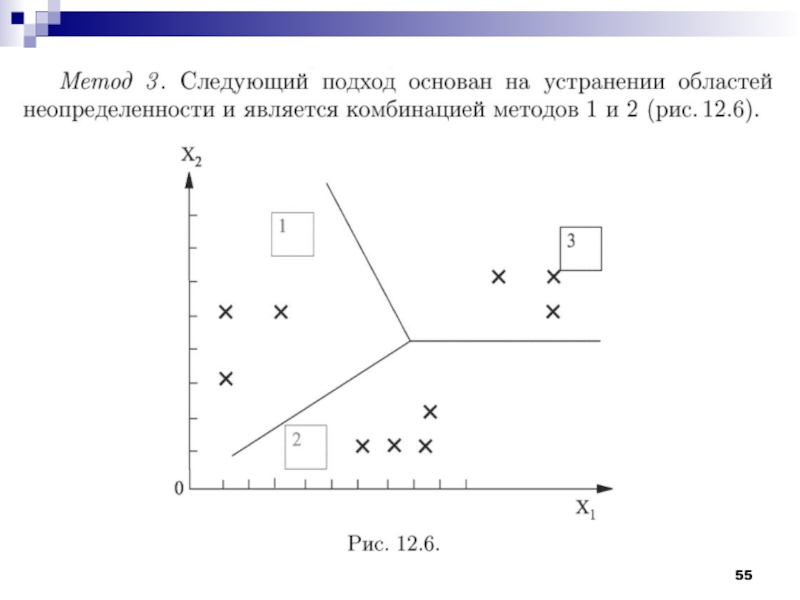
Слайд 8Рассмотрим работу алгоритма MAXMIN на примере. Как и в предыдущем
случае выберем объекты, которые заданы двумя признаками. Обучающая выборка представлена
на рис.
Слайд 28Проблемы алгоритма K-средних:
необходимо заранее знать количество кластеров.
алгоритм очень чувствителен
к выбору начальных центров кластеров. Классический вариант подразумевает случайный выбор
кластеров, что очень часто являлось источником погрешности. Как вариант решения, необходимо проводить исследования объекта для более точного определения центров начальных кластеров.не справляется с задачей, когда объект принадлежит к разным кластерам в равной степени или не принадлежит ни одному.
Слайд 31Нечеткий алгоритм кластеризации с-means
С последней проблемой k-means успешно справляется
алгоритм с-means. Вместо однозначного ответа на вопрос к какому кластеру
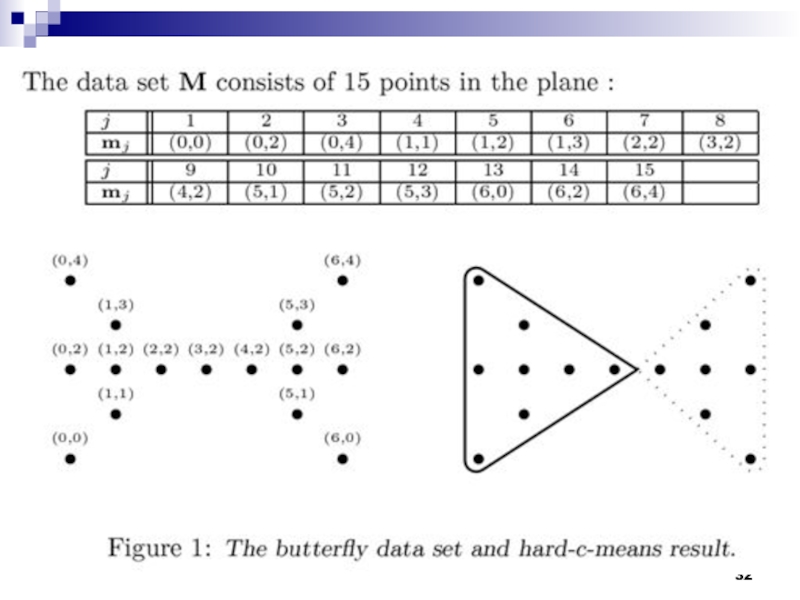
относится объект, он определяет вероятность того, что объект принадлежит к тому или иному кластеру. Таким образом, утверждение «объект А принадлежит к кластеру 1 с вероятностью 90%, к кластеру 2 — 10% » верно и более удобно.Классический пример с-means — т.н. «бабочка» (butterfly):
Слайд 33Алгоритм ISODATA (Iterative Self-Organizing Data Analysis Techniques) основывается на алгоритме
k средних, но включает набор оказавшихся полезными на практике эвристик
и параметры по их настройке. Одним из задаваемых априори параметров является желаемое число кластеров K.
Слайд 34Это число выступает в качестве рекомендации: в результате работы алгоритма
может быть построено как меньшее, так и большее число кластеров,
но оно будет не сильно отличаться от значения K. Сам алгоритм здесь детально описываться не будет (в целом, в нем используются те же шаги, что и в алгоритме k средних); приведем лишь основные эвристики.
Слайд 35Ликвидируются кластеры, в состав которых входит менее чем заданное число
элементов.
Для каждого текущего кластера определяется направление максимальной вытянутости. Наиболее вытянутый
кластер может быть расщеплен на два. 
Слайд 36Решение о расщеплении принимается с учетом размера кластера в направлении
вытянутости (этот размер может сравниваться с фиксированным порогом и отклонением
от среднего размера всех кластеров, а также общего числа кластеров, которое должно быть мало (с учетом параметра K).Попарно сливаются кластеры, расстояние между центрами которых меньше заданного порога, если число кластеров велико (с учетом параметра K).
Слайд 38Использующиеся в алгоритме ISODATA эвристики помогают не только подбирать более
подходящее число классов, но и находить более приемлемое решение, несколько
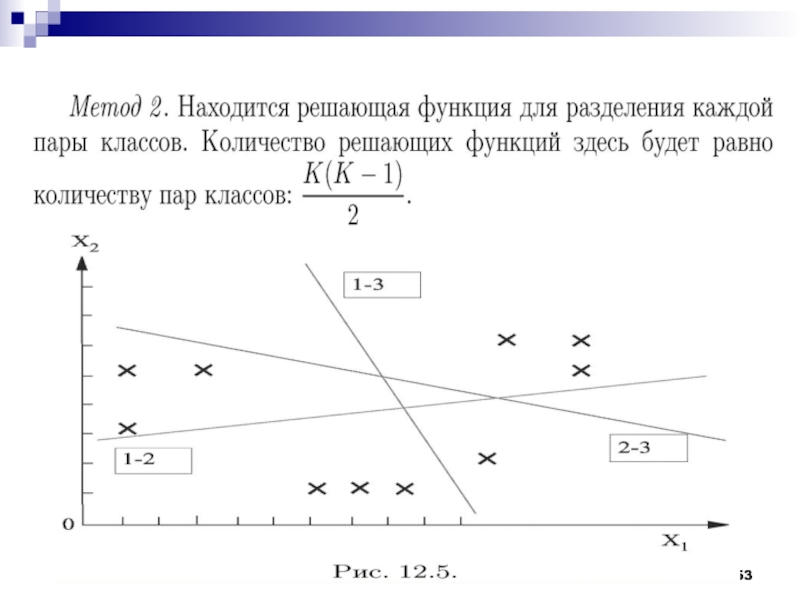
ослабляя (но не убирая полностью) зависимость от начальной гипотезы.
Слайд 56Задача минимизации количества решающих функций, достаточных для классификации образов, может
быть очень важна, особенно если количество классов d велико. Если
представить себе, с каким количеством классов объектов (или понятий) имеет дело человек, становится ясно, что решение этой проблемы в том или ином виде потребуется при разработке универсальной системы машинного обучения. Мы, однако, этот вопрос здесь рассматривать не будем, а перейдем к проблеме распознавания образов.
Слайд 59Прямого ответа на этот вопрос можно избежать, если конструировать методы
распознавания на основе неких эвристических соображений. Два наиболее широко распространенных
эвристических метода – это метод эталонных образов и метод ближайшего соседа.Метод эталонных образов
Метод эталонных образов – это один из эвристических методов построения решающих правил. В основу этого метода положена идея, которая заключается в том, что некоторая совокупность объектов, объединенных в отдельный класс, может быть представлена одним или несколькими эталонными объектами.
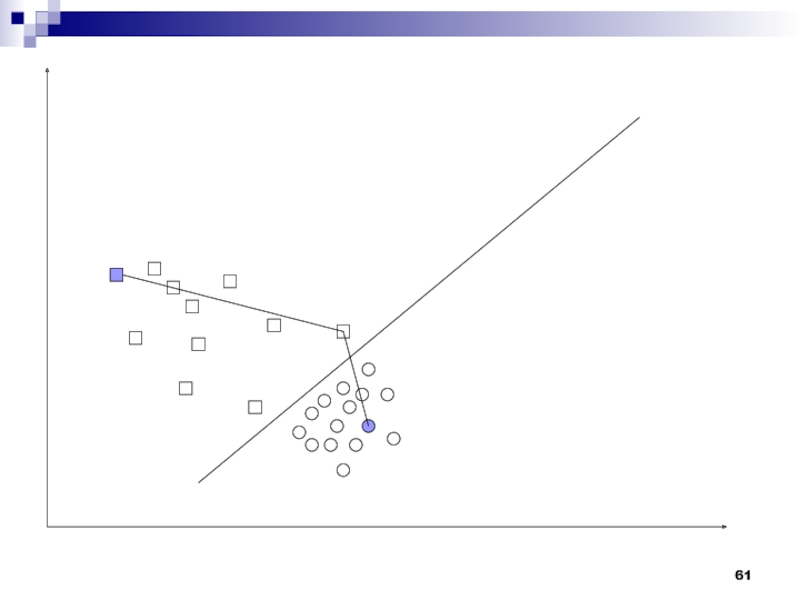
Слайд 60Эти эталонные объекты являются наиболее типичными представителями класса. Типичность эталонного
объекта означает, что он в среднем максимально похож на все
объекты класса.Поскольку сходство двух объектов может трактоваться как величина, противоположная расстоянию между ними в пространстве описаний (образов), то эталон – это объект, для которого минимально среднее расстояние до других объектов.
Слайд 62Классы, однако, могут обладать разными свойствами. Простейшим свойством является характерный
размер класса, который может быть оценен как
Слайд 65В соответствии с данным решающим правилом просматривается вся обучающая выборка,
в ней находится образ, расположенный наиболее близко к данному и
устанавливается, к какому классу он принадлежит (это известно, поскольку он находится в обучающей выборке). Этот класс и приписывается новому образу.
Слайд 66Метод ближайшего соседа весьма чувствителен к выбросам, то есть тем
образам обучающей выборки, для которых указаны ошибочные классы. В методе
k-ближайших соседей выбирается k образов обучающей выборки, наиболее близко расположенных к классифицируемому образу, и определяется, к какому классу относится больше всего из них. Поскольку выбросов, как правило, значительно меньше, чем правильных примеров, можно надеяться, что среди k ближайших соседей выбросов будет мало, и они не окажут влияния на результат классификации.
