Аналитическая

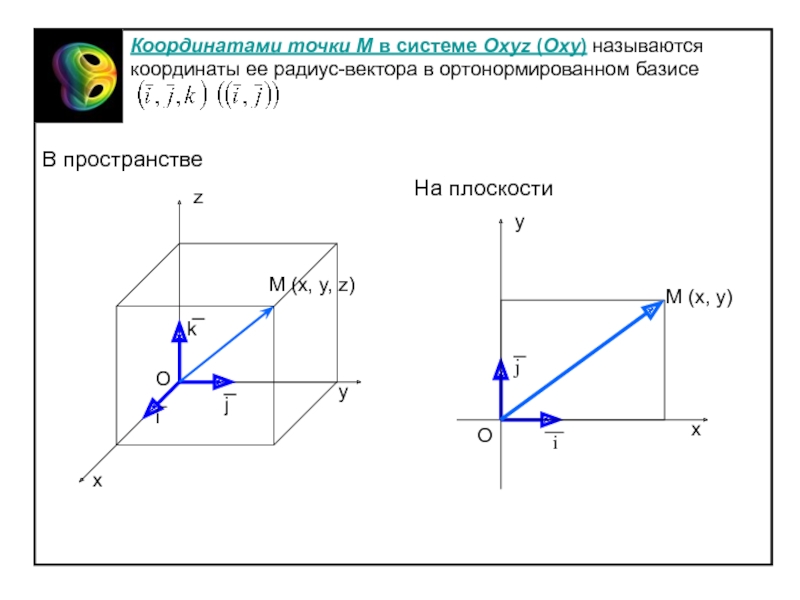
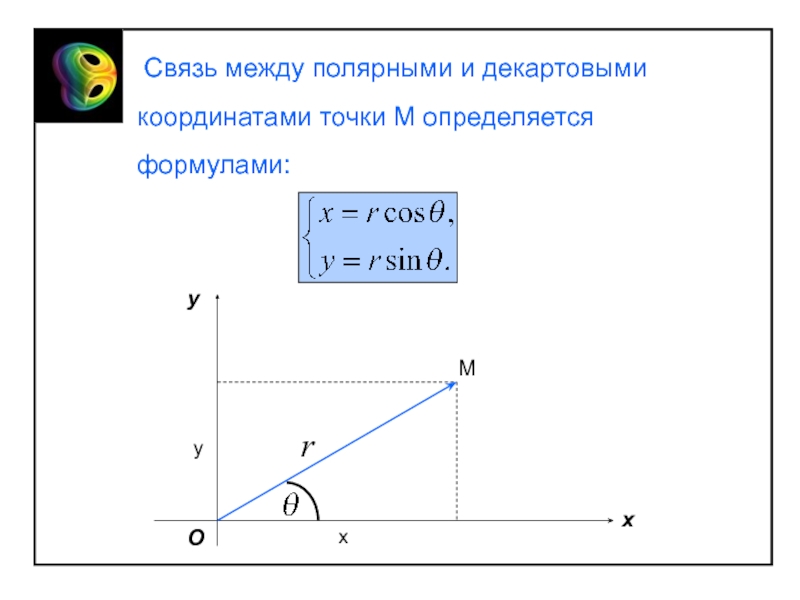
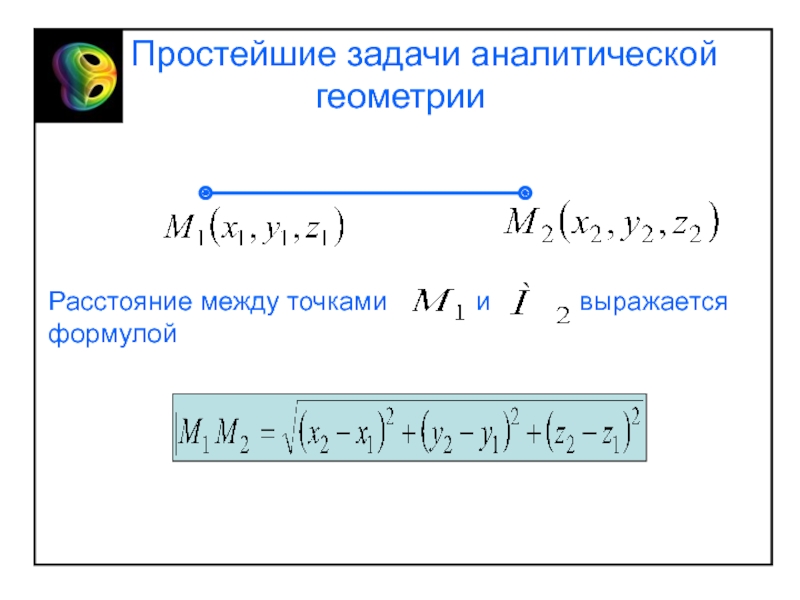
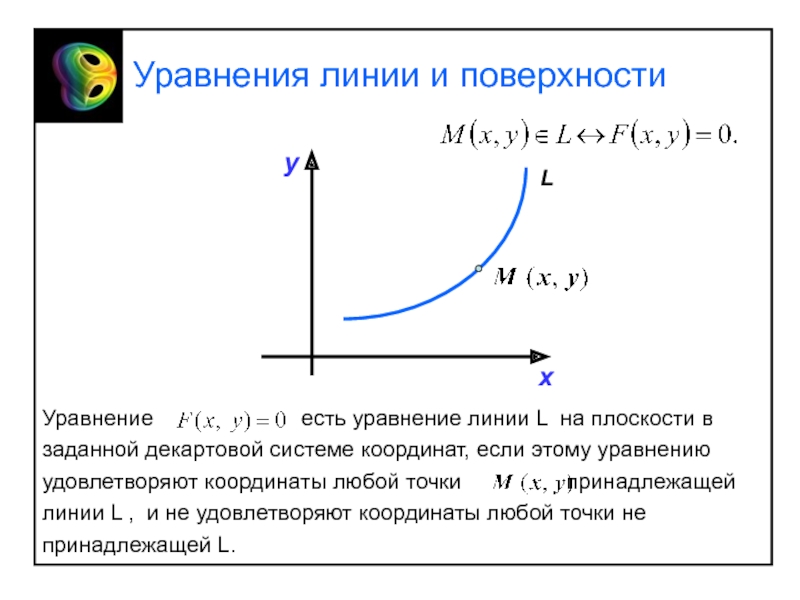
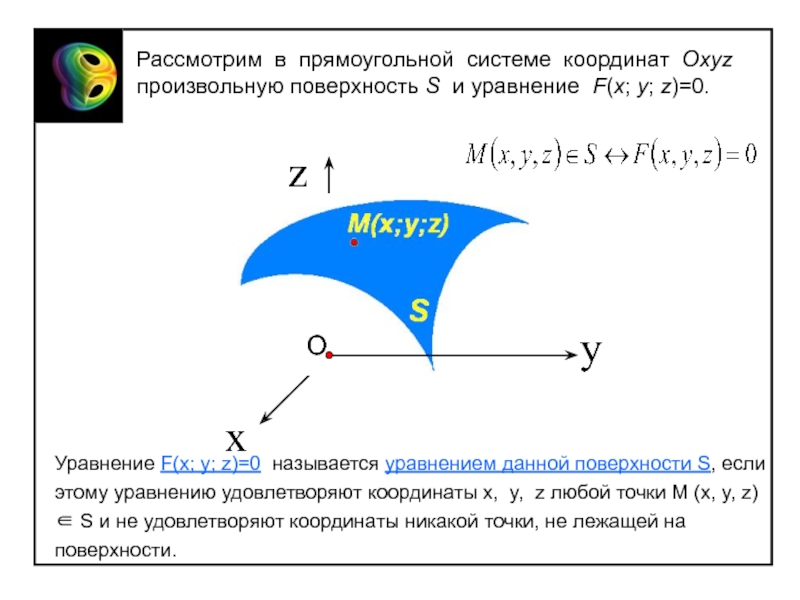
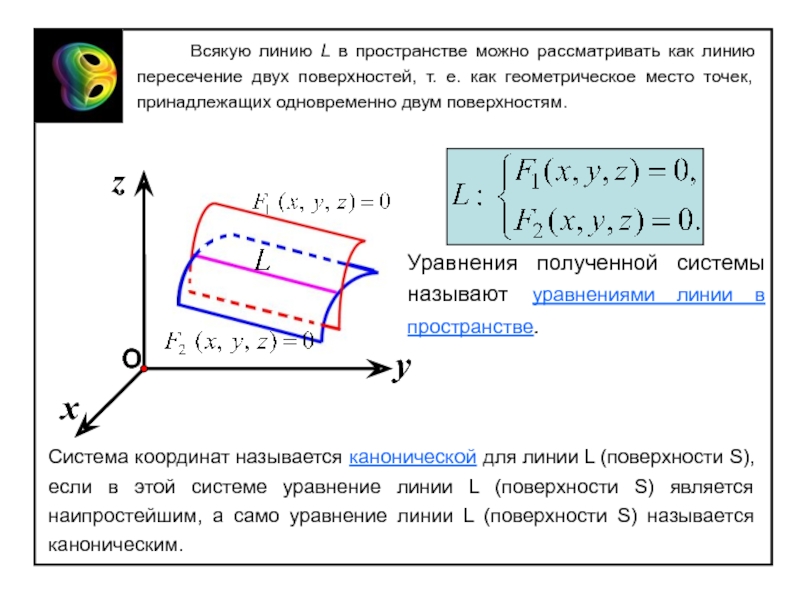
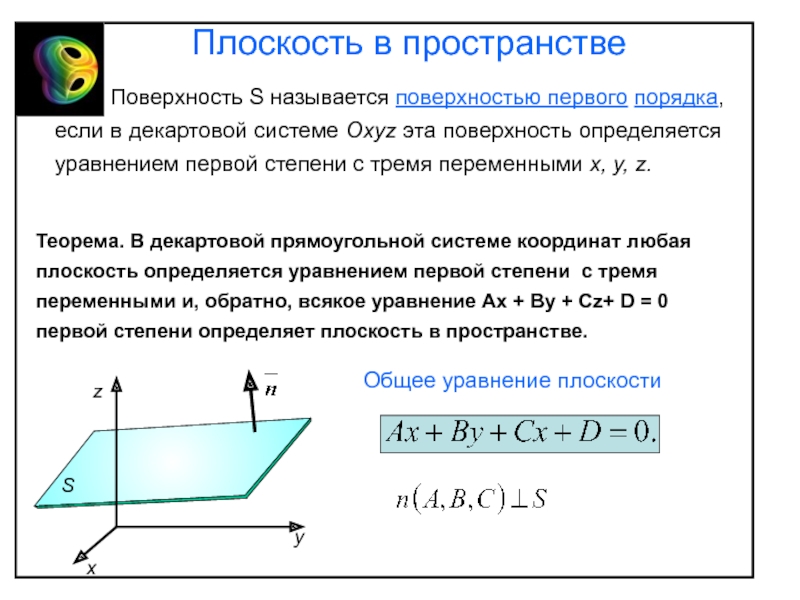
системой координат в пространстве (на плоскости) называется совокупность некоторой точки

Оси, проведенные через начало координат в направлении векторов , называются соответственно осями Ох, Оу, Оz (Ох, Оу).

Радиус-вектор точки М есть вектор

(Oxy) называются координаты ее радиус-вектора в ортонормированном базисе

точки М в системе Oxy и координатами

где - координаты в системе Oxy, а - направленный угол между осями и .

x

плоскости называется совокупность точки О, называемой полюсом, и выходящего из

Полярными координатами точки М на плоскости являются
- полярный радиус и - полярный угол,
причем

М

О

х

и

есть уравнение линии L

центром в точке

уравнение F(x; y; z)=0.
x
z
Уравнение F(x; y; z)=0 называется уравнением данной

рассматривать как линию пересечение двух поверхностей, т. е. как геометрическое

Уравнения полученной системы называют уравнениями линии в пространстве.

Система координат называется канонической для линии L (поверхности S), если в этой системе уравнение линии L (поверхности S) является наипростейшим, а само уравнение линии L (поверхности S) называется каноническим.

любая прямая определяется уравнением первой степени

Линия L на плоскости называется линией первого порядка, если в некоторой декартовой системе координат Oxy эта линия определяется уравнением первой степени относительно переменных x, y.

x

y

Общее уравнение прямой L на плоскости

C возможны следующие частные случаи:
 C = 0, А 

 А = 0, В  0, С  0 {By + C = 0}  прямая параллельна оси OX;

 В = 0, А  0, С  0 {Ax + C = 0} – прямая параллельна оси ОY;

 В = С = 0, А  0 – прямая совпадает с осью ОY;
 А = С = 0, В  0 – прямая совпадает с осью OX.

х

у

у

у

прямых

определяется формулой: