Слайд 1АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
Слайд 2Формы представления информации
Информационное сообщение может существовать
в самых разнообразных
видах и формах:
в виде знаков: это цифры и арифметические знаки,
используемые
в математике, условные графические
изображения;
в виде символов, которые могут быть представлены
буквами алфавита, специальными обозначениями, используемыми для создания текстов и рисунков;
в форме звуковых, световых сигналов и радиоволн,
применяемых в радиовещании, телефонии, телевизионной трансляции;
в форме устной речи;
в форме магнитных полей;
в форме электрического тока или напряжения, на которых основана работа двигателей, генераторов и других технических устройств
Слайд 3Единицы измерения количества информации
В электронно-вычислительных машинах используется объемный способ измерения
информации, учитывающий количество символов, содержащихся в сообщении.
Наименьшей единицей измерения
информации является Бит. Это двоичная ячейка памяти, которая может находиться в двух состояниях: «0» (тока нет) и «1» (ток есть).
Блоки данных, объединяющие 8 Бит, называют Байтами, а их номера — адресами (1 байт – минимальный адресуемый объем данных в ЭВМ). В свою очередь, определенная количественная совокупность Байт называется машинным словом (2 байта).
На практике чаще используют более крупные единицы измерения информации:
1 кБайт = 2^10 Байт;
1 МБайт = 2^20 Байт;
1 ГБайт = 2^30 Байт;
1 терабайт = 2^40 байт; 1 петабайт = 2^50 байт.
Слайд 4Кодирование информации
Информация разнообразных видов и форм кодируется, поступая в ЭВМ.
Кодирование
— перевод значения в двоичный код
Система счисления — это
способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.
В зависимости от способа изображения чисел системы делятся на
позиционные и непозиционные
Слайд 5В позиционной системе счисления количественное значение каждой цифры зависит от
ее местоположения (позиции) в числе.
В непозиционной системе счисления цифры не
меняют своего количественного значения при изменении их положения в числе. – РИМСКАЯ система
I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
Слайд 6Количество цифр, используемых для изображения числа в позиционной системе счисления,
называется основанием системы.
Десятичная (р = 10) система счисления — используется
в математике для записи числа, основание которого равно 10 (количеству используемых цифр от 0 до 9). Таким образом, любое число может быть представлено набором цифр с запятой или без нее. Если запятая присутствует, то последовательность чисел, расположенных до нее (запятой), называется целой частью числа. А последовательность чисел, расположенных после запятой, называется дробной частью числа.
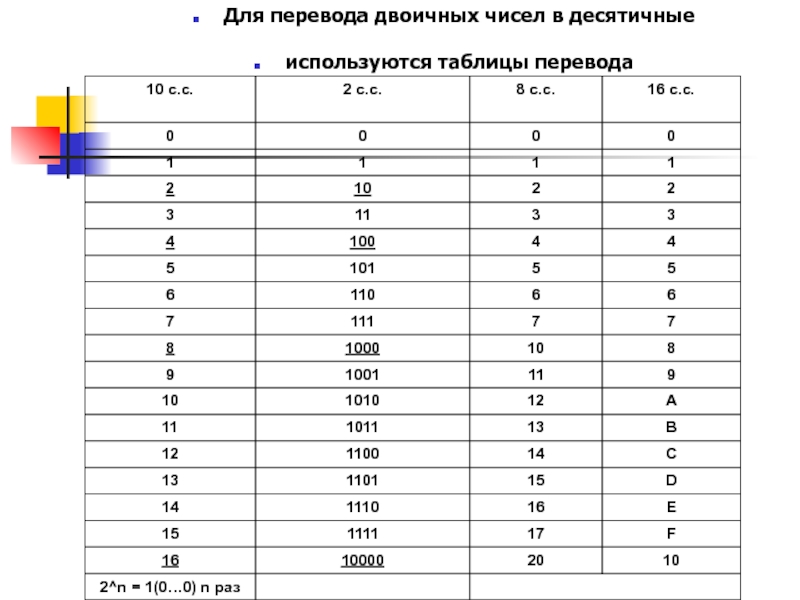
Слайд 7Для перевода двоичных чисел в десятичные
используются таблицы перевода
Слайд 8Алгоритм перевода десятичных чисел в двоичные. Целая часть
1.Разделить число на
2. Зафиксировать остаток (0 или 1) и частное.
2. Если частное
не равно 0, то разделить его на 2, и так далее, пока частное не станет равно 0. Если частное равно 0, то записать все полученные остатки, начиная с первого, справа налево.
В примере ответ 10111.
Слайд 9Алгоритм перевода десятичных чисел в двоичные. Дробная часть
1.Умножить дробную часть
на 2. Зафиксировать целую часть результата (0 или 1). 0,75*2=1,5
2.
Отбросить целую часть результата и продолжить умножение на 2. 0,5*2=1,0
Получить требуемое количество знаков после запятой. 0,11
Слайд 10Запись любого смешанного числа в системе счисления с основанием р
Запись
представляет собой ряд следующего вида:
am-1Pm-1+ am-2Pm-2+…+ a1P1+ a0P0+ a-1P-1+
+a-2P-2+…+
a-3P-3
где нижние индексы определяют местоположение цифры в числе (разряд):
положительные значения индексов — для целой части числа (m разрядов);
отрицательные значения — для дробной части
(s разрядов).
395,47110(10) = 3 • 102 + 9 • 101 + 5 • 100 + 4 •10-1 +
+ 7 •10-2 + 1 •10-3
Слайд 11Двоичная система счисления (р=2)
Используется для преобразования чисел в два символа
«0» и «1», а двоичное число 1011,01(2) представляется следующей последовательностью
:
1011,012= 1*23 + 0*22 + 1*21 + 1*2° + 0*2-1 + 1*2 -2 = 11,2510 (10).
Слайд 12Восьмеричная система счисления (р=8)
Кодирует информацию с помощью восьми символов (0
…7)
542,188= 5*82 + 4*81 + 2*8° + 1*8-1 + 8*8-2
= 354,2510
Шестнадцатеричная система счисления (р=16)
использует для кодирования 16 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А(10), В(11), С(12), D(13), E(14), F(15). Таким образом, запись F5C,E6 соответствует следующему ряду:
F5C,F616= F*162 + 5*161 + С*16° + Е*16-1 + 6*16-2 = 3932,910
Слайд 13ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК
Для анализа и синтеза схем в ЭВМ
при алгоритмизации и программировании решения задач широко используется математический аппарат
алгебры логики.
Алгебра логики – это раздел математической логики, значения всех элементов которой определены в двухэлементном множестве: 0 и 1 (ложь и истина).
Слайд 14Элементы алгебры логики
Основной объект алгебры логики – высказывание.
Высказыванием называется любое
предложение, о котором можно судить, истинно оно или ложно.
Высказывание должно
удовлетворять закону исключенного третьего, т.е. высказывание не должно быть одновременно истинным и ложным.
Слайд 15Операции алгебры логики
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ, КОНЪЮНКЦИЯ
(логическое И, &, )
Таблица истинности
A B AB
1 1 1
1 0 0
0 1 0
0 0 0
Схема
И
Слайд 16Операции алгебры логики
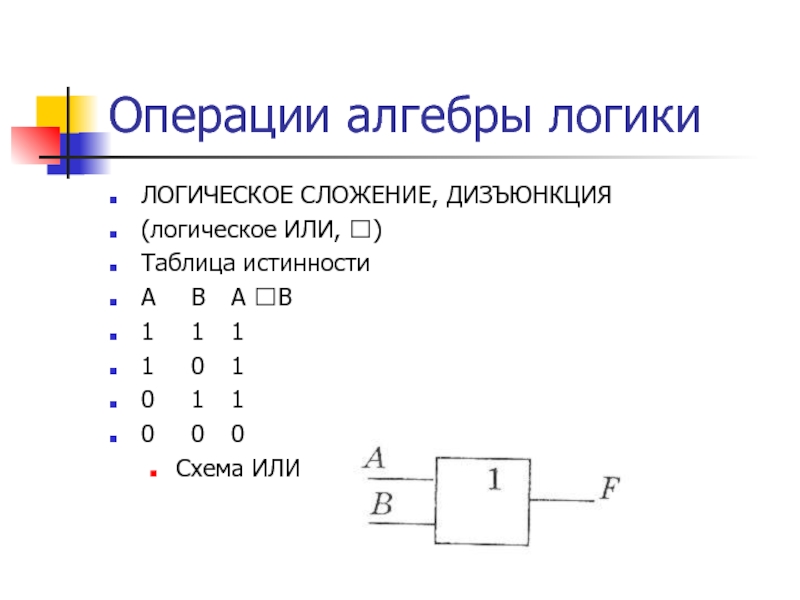
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ, ДИЗЪЮНКЦИЯ
(логическое ИЛИ, )
Таблица истинности
A B A B
1 1 1
1 0 1
0 1 1
0 0 0
Схема
ИЛИ
Слайд 17Операции алгебры логики
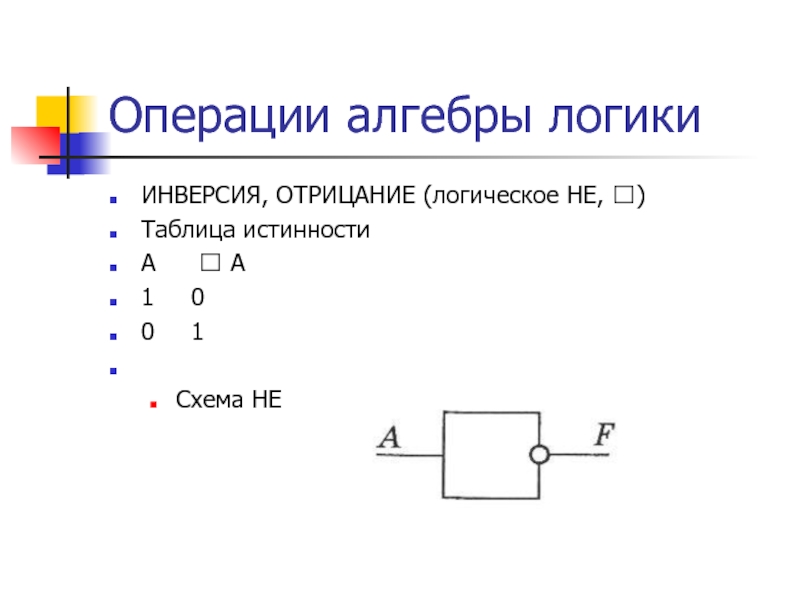
ИНВЕРСИЯ, ОТРИЦАНИЕ (логическое НЕ, )
Таблица истинности
A A
1 0
0 1
Схема
НЕ
Слайд 18Операции алгебры логики
ИМПЛИКАЦИЯ (логическое следование, «если…, то …», ->)
Таблица истинности
A B A
->B
1 1 1
1 0 0
0 1 1
0 0 1
Слайд 19Операции алгебры логики
ЭКВИВАЛЕНЦИЯ (A⬄B, тождественно, (“если и только если”, “необходимо
и достаточно”, “… равносильно …”)
Таблица истинности
A B A B
1 1 1
1 0 0
0 1 0
0 0 1
Слайд 20Законы алгебры логики
Сочетательный
(a+b)+c=a+(b+c); (a*b)*c=a*(b*c)
Переместительный
a+b=b+a; a*b=b*a
Распределительный
a*(b+c)=a*b+a*c
(a+b)*c=a*c+b*c
Слайд 21Законы
Поглощения
а и (а или с)=а; а или (а и с)=а
Склеивания
(а
или с) и (не а или с)=с
(а и с) или
(не а и с)=с
Непротиворечия а и не а=0
Исключенного третьего
а или не а = 1
Слайд 22Законы
Идемпотентности
а или а = а; а и а = а
Де
Моргана (общей инверсии)
Не(а или с)=не а и не с
Не(а и
с)=не а или не с
Исключения констант
A или 1 = 1; A или 0= А
A и 1 = A; A и 0= 0
Контрапозиции A -> B=не B -> не A
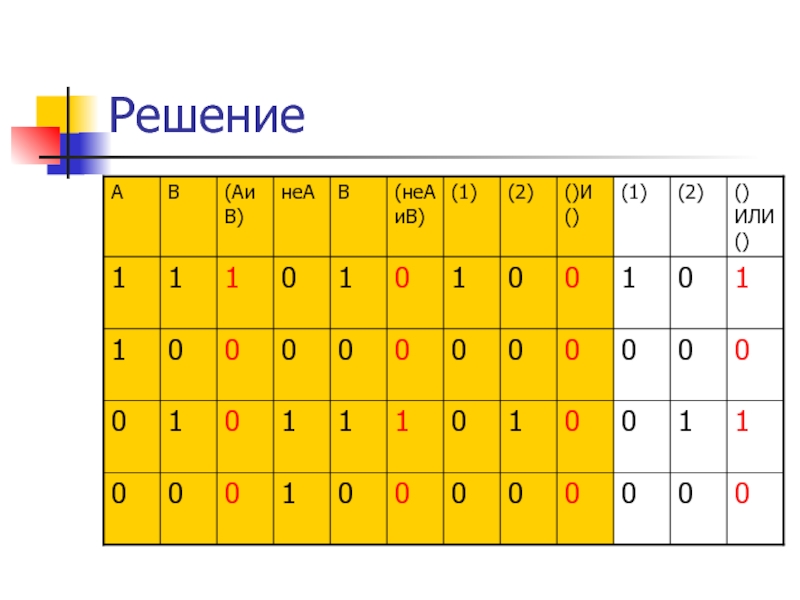
Слайд 23Задача
Для того, чтобы логическое выражение
(а И b) ? (НЕa
И b)
при любых значениях логических переменных а и b всегда
принимало значение "ложь", вместо знака вопроса...
можно поставить как знак дизъюнкции (V), так и знак конъюнкции(Л)
можно поставить знак конъюнкции (Л), но не знак дизъюнкции (V)
нельзя поставить ни знак дизъюнкции (V ), ни знак конъюнкции (Л)
можно поставить знак дизъюнкции (V), но не знак конъюнкции (Л)
Слайд 25В языке программирования QBasic логические операции используются в условном операторе
IF.
И – AND
ИЛИ - OR
НЕ – NOT
Пример:
IF x
x>2 THEN 10
IF x=2 OR x=7 THEN 20