Арифметические выражения

PRECISION или COMPLEX.
Простейшие виды арифметических выражений - это:
Константы.
Использование переменных.
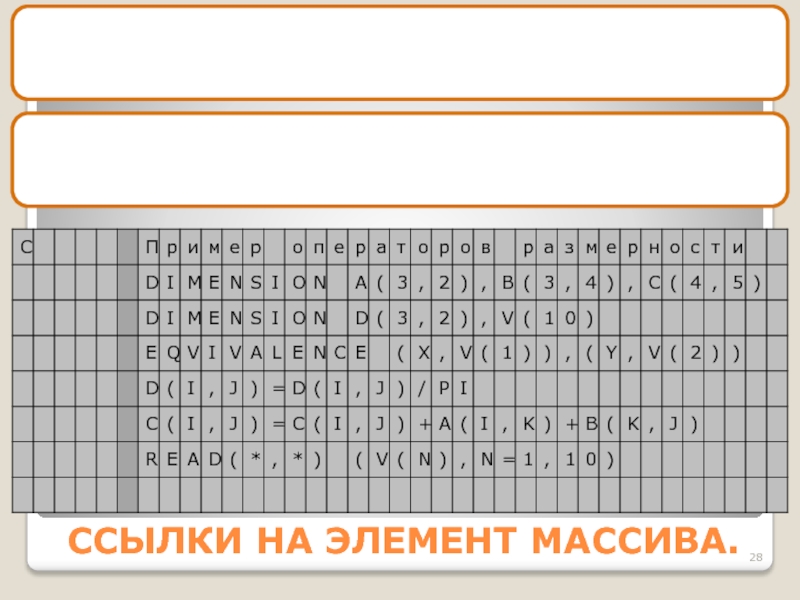
Использование элементов

того, как они появятся в арифметическом выражении.
Величины целых переменных должны

скобок и арифметических операторов.

между двумя операндами арифметического выражения.
Плюс (+) и минус (-) могут

Операции равного приоритета, за исключением возведения в степень выполняются слева направо.

Возведение в степень выполняется справа налево.

Каждое из следующих выражений слева эквивалентно выражению справа :

B
но можно: A * * (- B)

математическому частному двух этих величин, округленному до целого в сторону

Поэтому 7/3 превращается в 2,
а (-7)/3 превращается в -2.
Как 9/10, так и 9/(-10) равны нулю.

одного типа, то величина, являющаяся результатом этого выражения, этого же

Когда операнды разного типа, типом результата выражения является тип операнда максимального ранга.

Ранг операнда зависит от его типа данных соответственно следующему списку :
INTEGER * 2 (низший ранг)
INTEGER * 4
REAL * 4
REAL * 8
COMPLEX * 8
COMPLEX * 16 (высший ранг)

будет величина, относящаяся к типу данных
REAL*4.
Специальный случай:
операция над операндами

Дробный результат от деления в целой арифметике превращается в целое,

Поэтому следующие выражение равно нулю, а не единице : 1/4 + 1/4 + 1/4 + 1/4

или комбинацией действительного и целого операндов.
Но в следующем операторе сначала

:
Символьные константы.
Ссылки на символьные переменные.
Ссылки на элементы символьных массивов.
Любые символьные

выражений

с символьным, пока не определена метакоманда $NOTSTRICT.
В этом случае

Для сравнения величин в выражениях отношения можно использовать любой оператор, указанный в таблице:

операторов отношения нет относительного старшинства или сочетательности
поэтому выражение следующего вида

Выражения отношения могут появляться только в логических выражениях.

типа INTEGER и один операнд типа REAL
В этом случае перед

Выражения отношения символьных операндов сравнивают положение этих операндов в упорядоченной последовательности ASCII

Операнд является меньше чем другой, если он появляется раньше в упорядоченной последовательности.
Если сравниваются операнды разной длины, то более короткий рассматривается как дополненный справа пробелами до такой же длины как и длинный.

выражений следующие:
Логические константы.
Ссылки на логические переменные.
Ссылки на элементы логических массивов.
Ссылки

использованием скобок и логических операторов, указанных в таблице.

между двумя операндами логических выражений.
Оператор .NOT. - унарный и предшествует

Два .NOT. не могут соседствовать друг с другом.
Хотя A .AND. .NOT. B - это пример допустимого выражения с двумя операторами подряд.

.AND. C
.NOT. A .OR. B .AND. C
выполняется как (.NOT.

Операции равного приоритета выполняются слева направо, поэтому, например:

операторы отношения, они выполняются со следующими приоритетами :
Арифметические (высший).
Отношения

ссылаются в выражении, должны быть определены до момента ссылки.
Целые

нулевого операнда в нулевую или отрицательную степень и возведение отрицательного

массива.
Ее синтаксис следующий:
массив ( индекс [, индекс ] . .

в описании массива.
Величина индексного выражения должна находится между единицей и