Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
БГТУ ВОЕНМЕХ им. Д.Ф. Устинова Кафедра электротехники, О8
Содержание
- 1. БГТУ ВОЕНМЕХ им. Д.Ф. Устинова Кафедра электротехники, О8
- 2. Электрическая цепь, когда электрические сопротивления участков не
- 3. Расчёт электрических цепей Если сопротивление элемента электрической цепи
- 4. Расчёт электрических цепей Примеры линейной и нелинейной электрических
- 5. Графический расчет простейшей последовательной нелинейной резистивной схемыРасчёт нелинейных электрических цепей
- 6. Закон ОмаЗакон Ома для участка цепи, без
- 7. Составные части электрических цепейЭлектрическая цепь состоит из
- 8. Узел – это точка электрической цепи, где
- 9. Законы КирхгофаПервый закон КирхгофаАлгебраическая сумма мгновенных значений
- 10. В любом замкнутом контуре электрической цепи алгебраическая
- 11. Последовательность составления системы уравнений по законам Кирхгофа:Обозначаем
- 12. IIIузел aзамкнутый контур Iзамкнутый контур IIПример 1Расчёт электрических цепейЗаконы КирхгофаЦепь содержит:-3 ветви;- 2 узла.
- 13. Iчисло ветвей n=6Пример 2I1I2I3I4I5I6число узлов h=4}h-1=3}n-(h-1)=6-3=3Расчёт линейных электрических цепейЗаконы Кирхгофа
- 14. Баланс мощности Для проверки результатов расчета оставляем
- 15. Пример: Задана электрическая схема, со следующими параметрами:
- 16. Для расчета всех токов не хватает ещё
- 17. 7. Для проверки результатов вычислений, составим уравнения
- 18. Скачать презентанцию
Электрическая цепь, когда электрические сопротивления участков не зависят от направления и значения токов называется линейной электрической цепью. Такая цепь состоит из линейных элементов, токи напряжения которых могут быть найдены системой линейных
Слайды и текст этой презентации
Слайд 1БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова
Кафедра электротехники, О8
Лекция 2
Расчет электрических
цепей
Слайд 2 Электрическая цепь, когда электрические сопротивления участков не зависят от направления
и значения токов называется линейной электрической цепью.
Такая цепь состоит
из линейных элементов, токи напряжения которых могут быть найдены системой линейных уравнений. R
I
U
Обозначение и ВАХ линейного элемента
Расчёт электрических цепей
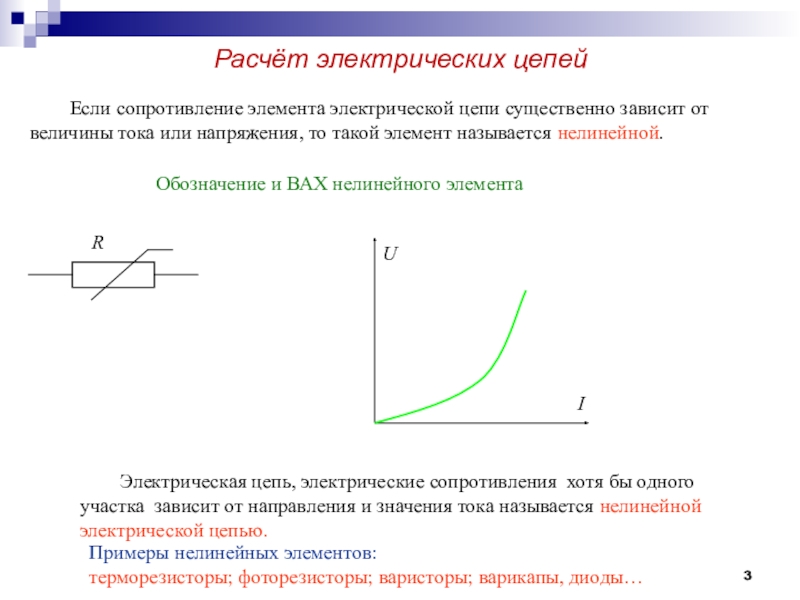
Слайд 3Расчёт электрических цепей
Если сопротивление элемента электрической цепи существенно зависит от
величины тока или напряжения, то такой элемент называется нелинейной.
Электрическая цепь,
электрические сопротивления хотя бы одного участка зависит от направления и значения тока называется нелинейной электрической цепью.R
U
I
Обозначение и ВАХ нелинейного элемента
Примеры нелинейных элементов:
терморезисторы; фоторезисторы; варисторы; варикапы, диоды…
Слайд 4Расчёт электрических цепей
Примеры линейной и нелинейной электрических цепей
Расчет нелинейных цепей
в основном ведут графическим методом.
R1
E
R2
U1
U2
I
E
RНЭ
U1
Uнэ
I
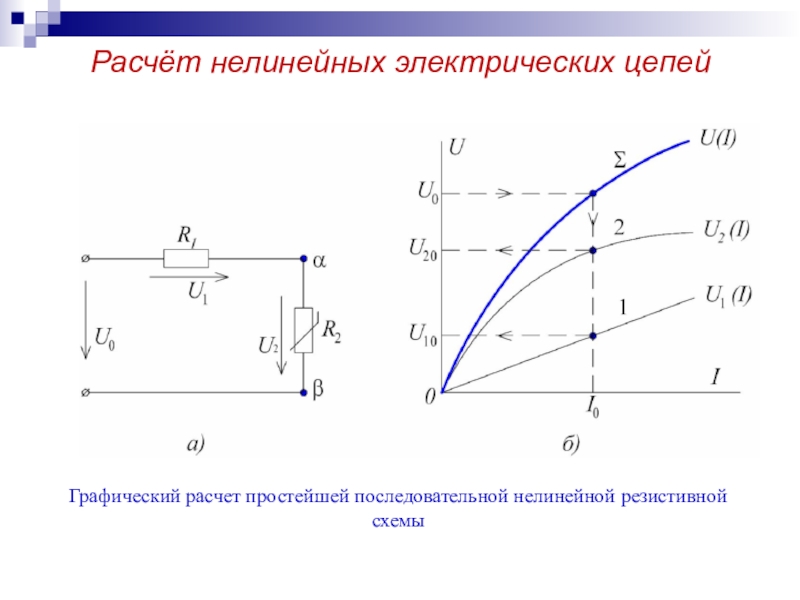
Расчет основывается графическим способов построения ВАХ
элементов и последовательности построения и вычисления.Данную тему изучаем самостоятельно!
Параграф 5.1 учебника «Электротехника и электрические машины»
Слайд 5Графический расчет простейшей последовательной нелинейной резистивной схемы
Расчёт нелинейных электрических цепей
Слайд 6Закон Ома
Закон Ома для участка цепи, без источника ЭДС
R
I
U
Сила тока
в участке цепи прямо пропорционально напряжению
на концах этого участка и
обратно пропорционально сопротивлению.Закон Ома для участка цепи, с источником ЭДС
Если направление тока, ЭДС и напряжения совпадают то напряжение и ЭДС
со знаком +, если нет то со знаком -.
Расчёт линейных электрических цепей
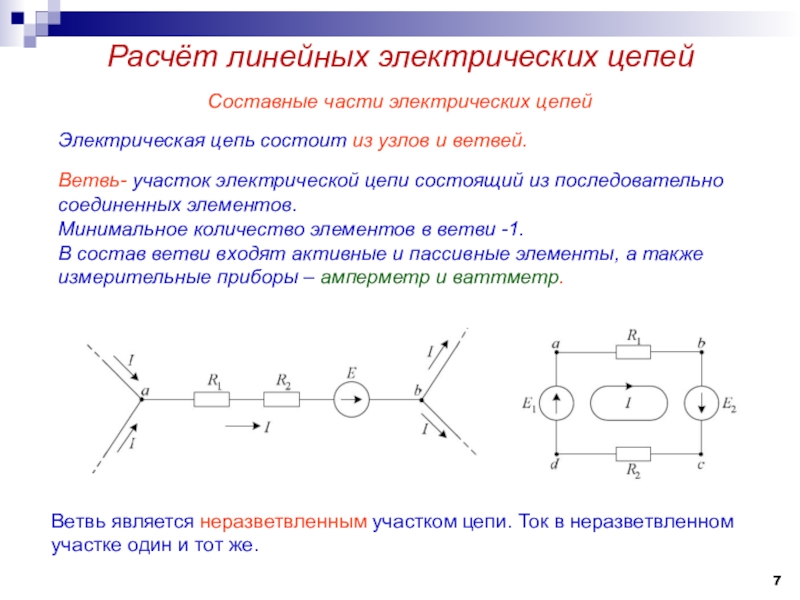
Слайд 7Составные части электрических цепей
Электрическая цепь состоит из узлов и ветвей.
Ветвь-
участок электрической цепи состоящий из последовательно соединенных элементов.
Минимальное количество
элементов в ветви -1.В состав ветви входят активные и пассивные элементы, а также измерительные приборы – амперметр и ваттметр.
Ветвь является неразветвленным участком цепи. Ток в неразветвленном участке один и тот же.
Расчёт линейных электрических цепей
Слайд 8Узел – это точка электрической цепи, где соединяются более трех
ветвей.
Разветвленная электрическая цепь – цепь содержащая три и более ветвей.
Контур
– любой замкнутый путь электрической цепи. В неразветвленной цепи всегда один контур. А в разветвленной цепи более двух.
Ветвь – участок цепи соединяющий узлы.
Ветвь – путь от одного узла до другого.
Составные части электрических цепей
Расчёт линейных электрических цепей
Слайд 9Законы Кирхгофа
Первый закон Кирхгофа
Алгебраическая сумма мгновенных значений токов в узле
равно нулю.
Сумма токов направленных к узлу электрической цепи равно сумме
токов направленных от узла.n – количество токов в ветвях
Пример:
Расчёт линейных электрических цепей
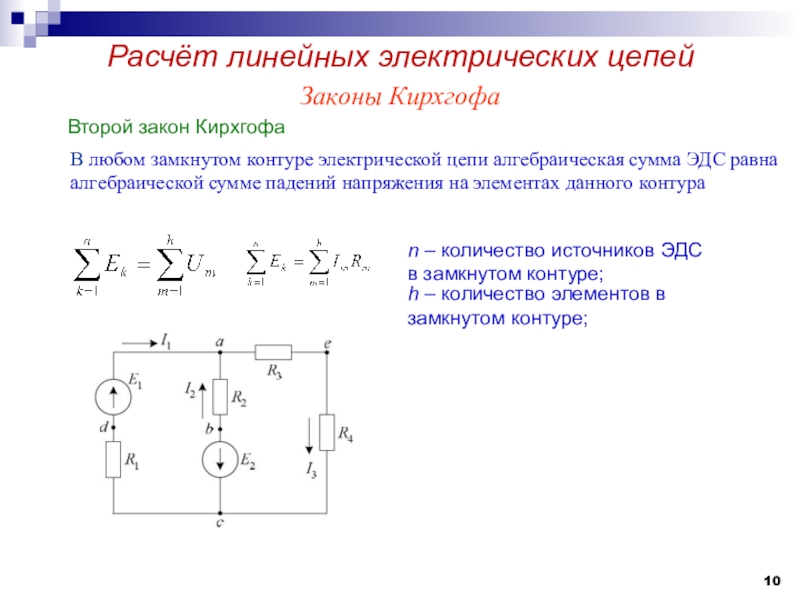
Слайд 10В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна
алгебраической сумме падений напряжения на элементах данного контура
n – количество
источников ЭДС в замкнутом контуре;h – количество элементов в замкнутом контуре;
Расчёт линейных электрических цепей
Законы Кирхгофа
Второй закон Кирхгофа
Слайд 11Последовательность составления системы уравнений по законам Кирхгофа:
Обозначаем (выбираем) произвольные направления
токов в ветвях цепи.
количество токов цепи равняется количеству ветвей -n
;Обозначим (отметим) узлы электрической цепи.
например, h;
Для h-1 узлов составляем уравнения на основании первого закона
Кирхгофа;
Выбираем (произвольно) независимые замкнутые контура.
Их количество равняется n-(h-1);
Для выбранных контуров составляем n-(h-1) уравнения
на основании второго закона Кигхгофа;
Расчёт линейных электрических цепей
Законы Кирхгофа
Слайд 12I
II
узел a
замкнутый контур I
замкнутый контур II
Пример 1
Расчёт электрических цепей
Законы Кирхгофа
Цепь
содержит:
-3 ветви;
- 2 узла.
Слайд 13I
число ветвей n=6
Пример 2
I1
I2
I3
I4
I5
I6
число узлов h=4
}
h-1=3
}
n-(h-1)=6-3=3
Расчёт линейных электрических цепей
Законы Кирхгофа
Слайд 14Баланс мощности
Для проверки результатов расчета оставляем баланс мощностей. На
основании закона сохранения энергии в электрической цепи:
Сумма мощностей, развиваемая источниками
энергии, должна быть равна сумме мощностей приемников: Пример
Расчёт линейных электрических цепей
Мощности источников и потребителей
рассчитываем на основании закона
Джоуля – Ленца.
Слайд 15Пример:
Задана электрическая схема, со следующими параметрами:
Найти токи во
всех ветвях и составить уравнение баланса мощностей
E1=52 В;
E2=69 В;
R01=
1 Ом;R02= 2 Ом;
R2= 5 Ом;
R3= 6 Ом;
R4= 3 Ом.
1. Зададим условно положительные направления токов в ветвях и обозначим их I1 – I6
2. Обозначим узлы, имеющиеся в схеме (a, b, c, d).
3. Составим уравнения на основе первого закона Кирхгофа для любых трех узлов из четырех:
для узла a → I1 + I3 – I4 = 0,
для узла b → I4 + I5 – I6 = 0,
для узла c → I2 – I3 – I5 = 0.
Слайд 16Для расчета всех токов не хватает ещё трёх уравнений.
4. Выберем
три независимых замкнутых контура и обозначим их римскими цифрами I,
II, III;5. Выберем условно положительные направления обхода (например, по часовой стрелке, как показано на рисунке)
6. Для выбранных контуров, составим уравнения на основании второго закона Кирхгофа:
Контур I →
Контур II →
Контур III →
Результаты вычислений:
I1 = 5 А, I2 = 6 А,
I3 = 2 А, I4 = 7 А,
I5 = 4 А, I6 = 11 А.
Слайд 177. Для проверки результатов вычислений, составим уравнения баланса мощностей:
674 Вт
= 674 Вт.
Результаты поверки баланса мощностей подтверждают правильность проведенных расчетов!
