Пирамида

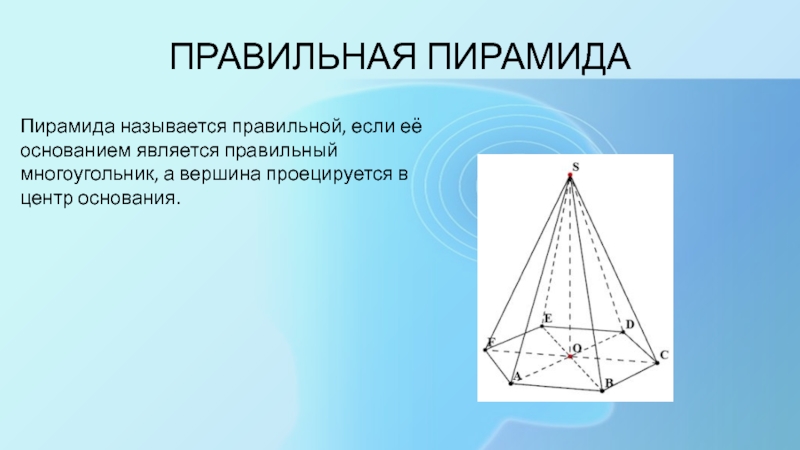
имеют одинаковую длину, при этом вершина пирамиды будет проецироваться в

2) Если боковые грани одинаково наклонены к плоскости основания, то около основания пирамиды можно описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности, а также высоты боковых граней имеют равную длину.

ребра равны, то высота, опущенная из вершины пирамиды, проецируется на

вершина проецируется в центр основания.

боковой грани (?)
S = 0,5Phа

пирамиды