Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Биквадратные уравнения
Содержание
- 1. Биквадратные уравнения
- 2. Актуализация знаний учащихся:Какое уравнение называется квадратным?Что называется
- 3. 5) Какое уравнение называется приведенным? 6) По
- 4. Найдите подбором корни уравнения: а)t²-3t+2=0б)t²-5t+4=0в)t²-20t+64=0г)t²-5t+6=0t₁=1; t₂=2t₁=1; t₂=4t₁=4; t₂=16t₁=2; t₂=3
- 5. ОПРЕДЕЛЕНИЕ Уравнение вида ах⁴+bх²+с=0, где а, b
- 6. Алгоритм решения биквадратного уравнения:Вводим в уравнение новую
- 7. 3) Решаем полученное квадратное уравнение;4) Способом подстановки
- 8. Пример1:х⁴-4х²+3=0х²=tt²-4t+3=0 t₁=3 ;t₂=11) x²=3 ;2) x²=1X=± x=±1Ответ: х₁,₂=±; х₃,₄=±1.
- 9. Пример2:x⁴-2x²-2=0x²=tt²-2t-2=0D=12t₁,₂=1±1) x²=1+2) x²=1-x₁,₂=±нет корнейОтвет: х₁,₂=±
- 10. Пример3:2х⁴-3х²+5=0х²=t2t²-3t+5=0D=9-4*2*5=9-40=-31Корней нетОтвет: корней нет.D
- 11. Пример4:9х⁴-6х²+1=0(3х²-1)²=03х²-1=0х²= х=±Ответ: х₁,₂=±
- 12. Пример5:х⁴+10х²+25=0(х²+5)²=0х²+5=0х²=-5нет корнейОтвет: корней нет.
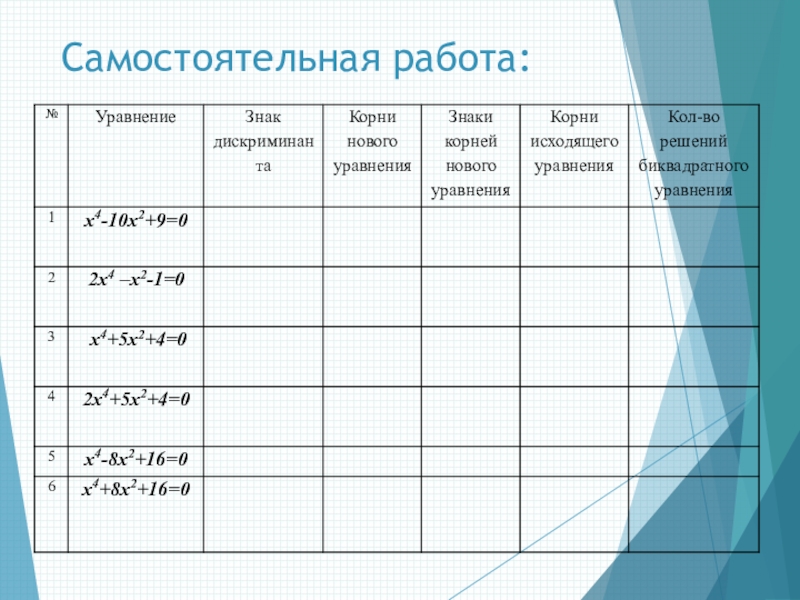
- 13. Самостоятельная работа:
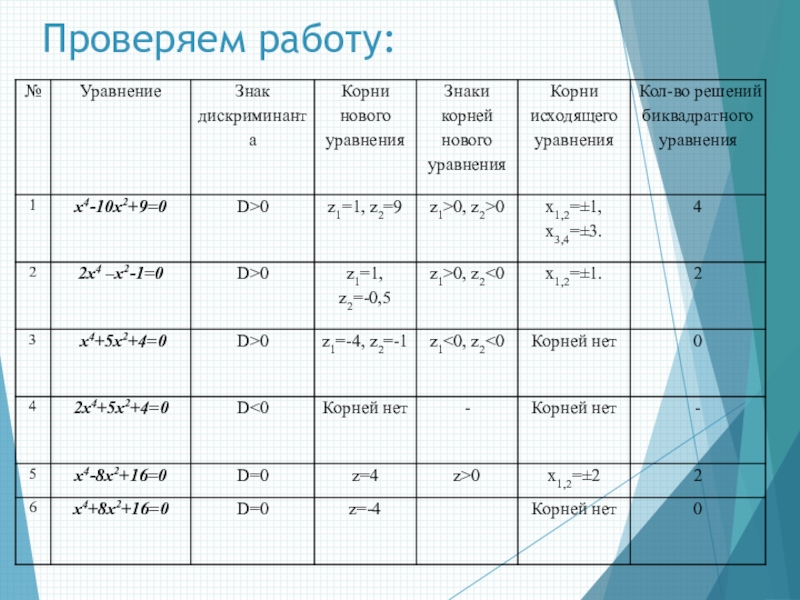
- 14. Проверяем работу:
- 15. 1. Какое уравнение называется биквадратным?2. Как решают биквадратные уравнения?3. Сколько корней может иметь биквадратное уравнение?Вопросы:
- 16. Домашнее задание:№776, 778
- 17. Спасибо за урок!
- 18. Скачать презентанцию
Актуализация знаний учащихся:Какое уравнение называется квадратным?Что называется дискриминантом квадратного уравнения?Какие виды квадратных уравнений вы знаете?Какое квадратное уравнение называется неполным?
Слайды и текст этой презентации
Слайд 2Актуализация знаний учащихся:
Какое уравнение называется квадратным?
Что называется дискриминантом квадратного уравнения?
Какие
виды квадратных уравнений вы знаете?
Слайд 35) Какое уравнение называется приведенным?
6) По каким формулам находятся
корни квадратных уравнений?
7) Сформулируйте теорему Виета.
8) Сформулируйте обратную теорему Виета.
Слайд 4Найдите подбором корни уравнения:
а)t²-3t+2=0
б)t²-5t+4=0
в)t²-20t+64=0
г)t²-5t+6=0
t₁=1; t₂=2
t₁=1; t₂=4
t₁=4; t₂=16
t₁=2; t₂=3
Слайд 5ОПРЕДЕЛЕНИЕ
Уравнение вида
ах⁴+bх²+с=0,
где а, b и с –данные
числа и а≠0,
а х - неизвестное, называют
биквадратным уравнением.
х²
= tat²+bt+c=0
Слайд 6Алгоритм решения биквадратного уравнения:
Вводим в уравнение новую переменную путем обозначения
какого- то выражения из этого уравнения;
Вместо этого выражения подставляем новую
переменную и получим квадратное уравнение относительно новой переменной; 
Слайд 73) Решаем полученное квадратное уравнение;
4) Способом подстановки находим значение исходной
переменной;
5) С помощью проверки определяем корни данного уравнения.
Слайд 151. Какое уравнение
называется биквадратным?
2. Как решают биквадратные
уравнения?
3. Сколько
корней может иметь биквадратное уравнение?
Вопросы:
