Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Биомеханика кровообращения
Содержание
- 1. Биомеханика кровообращения
- 2. 1. Общее представление о строении системы кровообращенияСердце
- 3. Система легочных сосудов — легочные артерии, капилляры и вены — образует малый (легочный) круг кровообращения.
- 4. Обогащенная кислородом кровь из легких по легочным
- 5. Система этих сосудов образует большой круг кровообращения.
- 6. Слайд 6
- 7. 2. Основные параметры гемодинамики. Линейная и объёмная
- 8. Скорость перемещения самих частиц жидкости (или плывущих
- 9. Однако, на практике чаще важнее знать объём
- 10. Между линейной скоростью υ и объёмной скоростью
- 11. Слайд 11
- 12. Выделим поперечный слой жидкости, который в момент
- 13. Объёмная скорость жидкости Q при этом будет
- 14. Так как жидкость крайне мало сжимаема, то
- 15. Отсюда следует закон постоянства расхода жидкости (условие неразрывности струи):
- 16. Таким образом, если мы имеем дело с
- 17. На основании уравнения неразрывности струи можно качественно
- 18. Схема разветвления сосудов в большом круге
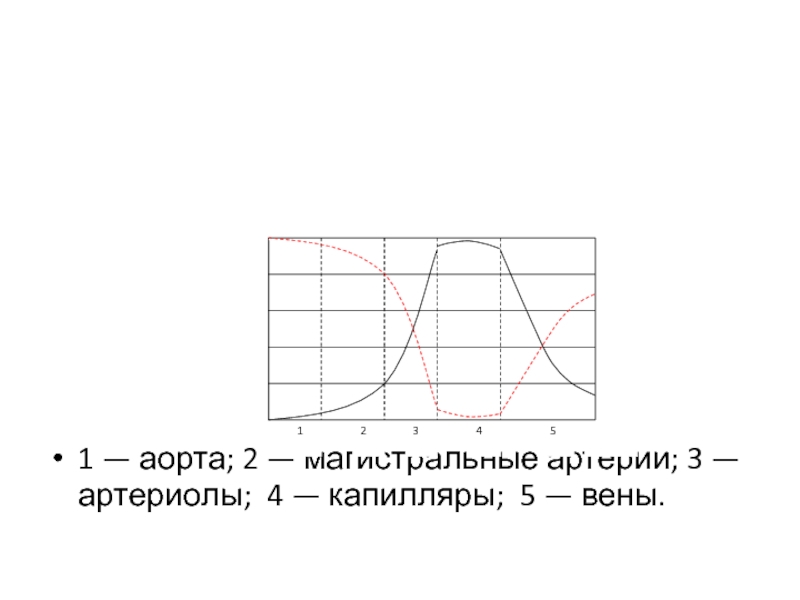
- 19. 1 — аорта; 2 — магистральные артерии; 3 — артериолы; 4 — капилляры; 5 — вены.
- 20. 3. Течение идеальной жидкости. Теорема Бернулли.
- 21. Считалось, что таких жидкостей не существует, но
- 22. Установившееся течение (стационарное) - такое течение, при
- 23. Уравнение Бернулли справедливо для стационарного движения идеальной
- 24. В потоке идеальной жидкости сумма статического, гидростатического и гидродинамического давлений есть величина постоянная.
- 25. р – внешнее статическое давление, которое, согласно
- 26. Для горизонтального течения жидкости, когда ρgh = const, можно уравнение Бернулли упростить:
- 27. Статическое давление - это то давление, которое
- 28. Слайд 28
- 29. Из теоремы Бернулли следует, что там, где
- 30. Практическое значение уравнения Бернулли1) При сильном ветре
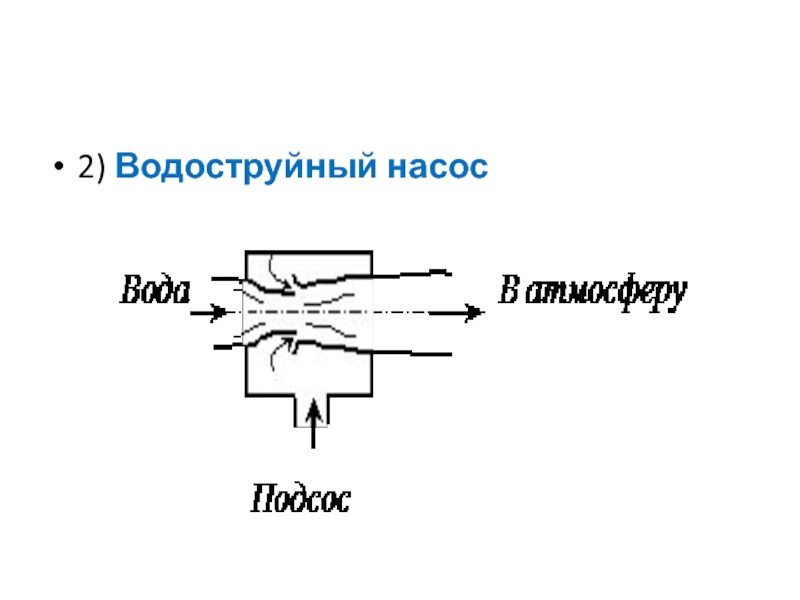
- 31. 2) Водоструйный насос
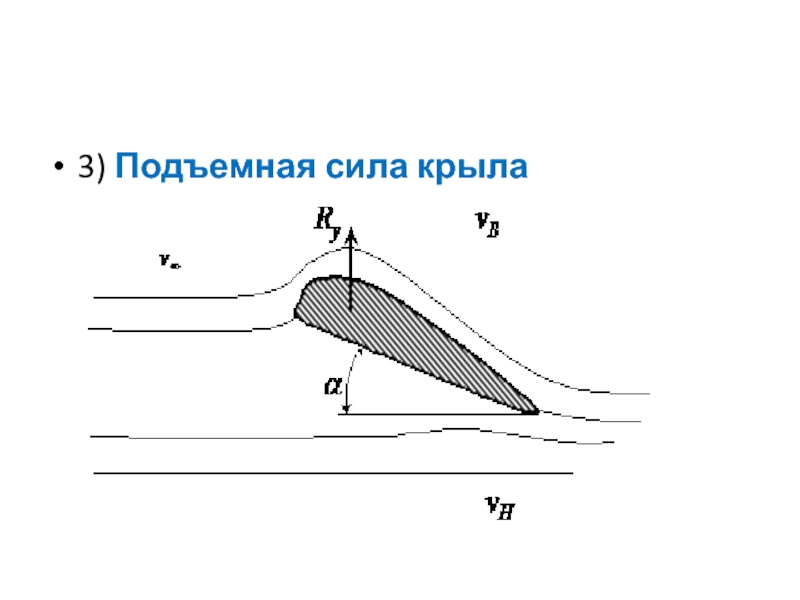
- 32. 3) Подъемная сила крыла
- 33. 4) Закупорка артерии. Артериальный шум.
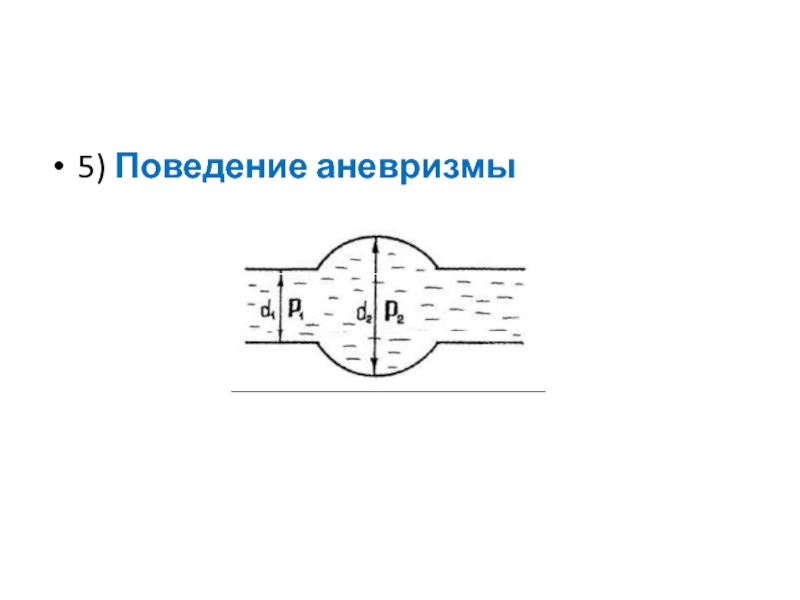
- 34. 5) Поведение аневризмы
- 35. 4. Ламинарное течение жидкости, формула Пуазейля.
- 36. Формула Пуазейля позволяет рассчитать объёмную скорость течения
- 37. Как и можно было ожидать, объёмная скорость
- 38. Интересно сравнить движение жидкости с электрическим током (движением электрических зарядов).
- 39. Запишем формулу Пуазейля в таком виде:
- 40. В первой формуле слева стоит причина течения
- 41. Очевидно, что величина имеет смысл сопротивления движению
- 42. Используя это обозначение, можно формулу Пуазейля записать
- 43. Гемодинамическое сопротивление (Rr) разных отделов кровеносного
- 44. 5. Элементы биомеханики сердца. Работа, совершаемая
- 45. Работа, совершаемая сердцем, затрачивается, во-первых, на выталкивание
- 46. Статический компонент работы сердца вычисляется по формуле:
- 47. Изменение КД в артериях является сложной периодической функцией:
- 48. Поэтому среднее давление равно не полусумме максимального
- 49. Следовательно, оно определяется так:Среднее давление – одна из гомеостатических констант организма.
- 50. Величина рср в большом круге кровообращения составляет
- 51. Поскольку Vc обоих желудочков одинаков, а давление,
- 52. Кинетический компонент работы сердца определяется по формуле:где
- 53. Следовательно, Аk = 103 кг. м-3. 70.10-6
- 54. Поэтому при физических и психических нагрузках вклад
- 55. 6. Биофизические особенности аорты. Пульсовая волна
- 56. Аст миокарда затрачивается на растяжение стенок артерий
- 57. Упругость аортальной стенки обусловливает еще одно важное
- 58. Слайд 58
- 59. Непрерывность кровотока обеспечивается первой из них,
- 60. Пульсовая волна распространяется от места своего возникновения
- 61. Общую характеристику пульсовой волны врач получает при
- 62. Записав сфигмограммы в двух точках артериальной магистрали
- 63. С возрастом скорость пульсовой волны увеличивается. Чем
- 64. 7. Биофизические особенности артериол большого круга
- 65. Слайд 65
- 66. Из-за малого радиуса артериолы обладают наибольшим гемодинамическим
- 67. Но каждая артериола снабжает кровью около 100
- 68. Слайд 68
- 69. Так как разность давлений (падение давления) на
- 70. В стенках мелких артерий (и особенно –
- 71. В результате растёт гемодинамическое сопротивление и, соответственно,
- 72. Важно отметить, что во всех названных случаях
- 73. Таким образом, артерии мышечного типа, особенно артериолы
- 74. Кроме того, еще И.М. Сеченов называл артериолы
- 75. 8. Транспорт веществ через стенку капилляра
- 76. Физиологическое значение капилляров состоит в том, что
- 77. Большое значение в обмене веществ между кровью
- 78. Так, гидростатическое давление в артериальном конце капилляра
- 79. Вследствие фильтрации содержимое плазмы крови поступает в
- 80. Факторы, обусловливающие обратный транспорт, составляют: Онкотическое давление
- 81. Факторы, противодействующие обратному транспорту: Гидростатическое давление крови
- 82. Отсюда, давление, обеспечивающее обратный транспорт, составляет: 27 - 21 = 6 мм. рт. ст.
- 83. Подсчитано, что за один час фильтруется около
- 84. 9. Движение крови в венах Движение
- 85. Даже если давление в венозной системе повысится
- 86. Таким образом, вены (а также сосуды малого круга кровообращения) являются резервуаром крови переменной емкости.
- 87. Скачать презентанцию
1. Общее представление о строении системы кровообращенияСердце и кровеносные сосуды составляют систему кровообращения.Оттекающая от тканей венозная кровь поступает в правое предсердие, а оттуда в правый желудочек сердца. При сокращении его кровь
Слайды и текст этой презентации
Слайд 1ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ
имени С.М. Кирова
Кафедра биологической и медицинской физики
ЛЕКЦИЯ № 15
по
дисциплине «Физика, математика»
курса ФПВ, ФПиУГВ, спецфакультетаСлайд 21. Общее представление о строении системы кровообращения
Сердце и кровеносные сосуды
составляют систему кровообращения.
Оттекающая от тканей венозная кровь поступает в правое
предсердие, а оттуда в правый желудочек сердца. При сокращении его кровь нагнетается в легочную артерию. Протекая через легкие, она отдает СО2 и насыщается О2. Слайд 3
Система легочных сосудов — легочные артерии, капилляры и вены —
образует малый (легочный) круг кровообращения.
Слайд 4
Обогащенная кислородом кровь из легких по легочным венам поступает в
левое предсердие, а оттуда в левый желудочек.
При сокращении последнего кровь
нагнетается в аорту, артерии, артериолы и капилляры всех органов и тканей, а оттуда по венам притекает в правое предсердие. Слайд 72. Основные параметры гемодинамики. Линейная и объёмная скорости движения жидкости;
связь между ними. Условие неразрывности струи
Основной характеристикой любого движения является
его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах.
Слайд 8
Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью
мелких тел – например, эритроцитов в крови) обозначают υ
и называют линейной скоростью.[м/с]
Слайд 9
Однако, на практике чаще важнее знать объём V жидкости, протекающей
через поперечное сечение данного потока (трубы, русла реки, кровеносного сосуда
и т.п.) за единицу времени.Эту величину называют объёмной скоростью и обозначают Q.
[м3/с]
Слайд 10
Между линейной скоростью υ и объёмной скоростью Q существует простая
связь.
Рассмотрим трубку с площадью поперечного сечения S.
Слайд 12
Выделим поперечный слой жидкости, который в момент времени t =
0 занимает положение 1.
Через некоторое время t он переместится
в положение 2, отстоящее на расстояние x = υt .
При этом через трубку пройдёт объём жидкости V = Sx .
Слайд 14
Так как жидкость крайне мало сжимаема, то объем, протекающий за
единицу времени через любое сечение трубки, одинаков, то есть объемная
скорость Q на протяжении всей трубки постоянна.Слайд 16
Таким образом, если мы имеем дело с жесткой неразрывной трубой
переменного сечения, то линейная скорость течения жидкости тем больше, чем
меньше сечение трубы.Слайд 17
На основании уравнения неразрывности струи можно качественно объяснить изменения скорости
течения крови в системе кровообращения.
Sаорты = 4 см2; Vаорт.= 0,5-1
м/с (до 20 м/с при физических нагрузках)Sкап. = 11.000 см2 (обычно 3.000 см2) ;
Vкап.= 1 мм/с
Слайд 18 Схема разветвления сосудов в большом круге кровообращения (модель разветвленной сосудистой
трубки).
1 — аорта; 2 — капиллярное русло;
3 — полые вены (верхняя и нижняя).
Слайд 20
3. Течение идеальной жидкости. Теорема Бернулли.
Идеальная жидкость – жидкость абсолютно
несжимаемая и не имеющая внутреннего трения (вязкости).
Следовательно, при движении
жидкости не происходит диссипация энергии (переход механической энергии в тепло).Слайд 21
Считалось, что таких жидкостей не существует, но в 1938 году
академик П.Л.Капица обнаружил, что при температурах, очень близких к абсолютному
нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью»; за открытие и исследование этого явления ему в дальнейшем была присуждена Нобелевская премия).Слайд 22
Установившееся течение (стационарное) - такое течение, при котором характер движения
жидкости не меняется (любая частица жидкости проходит данную точку пространства
с одним и тем же значением скорости).Слайд 23
Уравнение Бернулли справедливо для стационарного движения идеальной несжимаемой жидкости и,
по сути, выражает закон сохранения механической энергии для движущейся жидкости.
Слайд 24
В потоке идеальной жидкости сумма статического, гидростатического и гидродинамического давлений
есть величина постоянная.
Слайд 25
р – внешнее статическое давление, которое, согласно закону Паскаля, передается
жидкостью во все стороны без изменения.
ρgh - давление силы
тяжести жидкости, или гидростатическое давление. - динамическое давление, направленное по вектору скорости жидкости.
Слайд 26
Для горизонтального течения жидкости, когда ρgh = const, можно уравнение
Бернулли упростить:
Слайд 27
Статическое давление - это то давление, которое движущаяся жидкость оказывает
на стенки трубки.
Динамическое давление – это давление, которая движущаяся
жидкость оказывает на преграду ее течению (не действует на стенки).Слайд 29
Из теоремы Бернулли следует, что там, где скорость жидкости или
газа больше, статическое давление меньше,
и наоборот.Слайд 30Практическое значение уравнения Бернулли
1) При сильном ветре динамическое давление сильно
возрастает (пропорционально квадрату скорости ветра), поэтому статическое давление над крышей
значительно падает.Под крышей, где нет движения воздуха, статическое давление остаётся высоким; разность давлений срывает листы кровли вверх.
Слайд 35
4. Ламинарное течение жидкости, формула Пуазейля.
Рассмотрим часто встречающийся случай ламинарного
движения жидкости по трубке с круглым сечением под действием разности
давлений на её концах.Слайд 36
Формула Пуазейля позволяет рассчитать объёмную скорость течения жидкости по известным
значениям радиуса трубки r, её длины L, вязкости жидкости η
и разности давлений на концах трубки p1 – р2.
Слайд 37
Как и можно было ожидать, объёмная скорость прямо пропорциональна разности
давлений и обратно пропорциональна вязкости.
Обращает на себя внимание очень
сильная зависимость объёмной скорости от радиуса: Q ~ r4. Слайд 38
Интересно сравнить движение жидкости с электрическим током (движением электрических зарядов).
Слайд 39
Запишем формулу Пуазейля в таком виде:
р1 – р2 =
и сравним её с
формулой закона Ома, написанной так: U1 – U2 = R.I . Легко видеть, что между этими формулами существует аналогия.
Слайд 40
В первой формуле слева стоит причина течения жидкости -разность давлений,
во второй - причина возникновения тока, то есть разность потенциалов.
Справа в первой формуле стоит объёмная скорость, то есть количество жидкости, протекающее в единицу времени; во второй формуле - сила тока, то есть количество зарядов, протекающее в единицу времени.
Слайд 41
Очевидно, что величина
имеет смысл сопротивления движению жидкости.
Ее так
и называют - гидродинамическое сопротивление.
RГД =
Слайд 42
Используя это обозначение, можно формулу Пуазейля записать в таком виде:
p1
– p2 = RГД.Q или Q =
Слайд 43
Гемодинамическое сопротивление (Rr) разных отделов кровеносного русла:
1 — аорта; 2
— магистральные артерии; 3 — артериолы; 4 — капилляры;
5 — вены.Слайд 44 5. Элементы биомеханики сердца. Работа, совершаемая сердцем, ее статический и
динамический компоненты
Механическая работа, совершаемая сердцем, развивается за счет сократительной деятельности
миокарда. Вслед за распространением возбуждения происходит сокращение миокардиальных волокон.
Слайд 45
Работа, совершаемая сердцем, затрачивается, во-первых, на выталкивание крови в магистральные
артериальные сосуды против сил давления и, во-вторых, на придание крови
кинетической энергии.Первый компонент работы называется статическим (потенциальным), а второй — кинетическим.
Слайд 46
Статический компонент работы сердца вычисляется по формуле:
Аст = рcpVc
где
рср — среднее давление крови в соответствующем магистральном сосуде (аорте
— для левого желудочка, легочном артериальном стволе — для правого желудочка), Vc – систолический объем.Слайд 48
Поэтому среднее давление равно не полусумме максимального (систолического) и минимального
(диастолического) давлений, а среднему из бесконечно малых изменений давления от
максимального до минимального в течение одного сердечного цикла.Слайд 49
Следовательно, оно определяется так:
Среднее давление – одна из гомеостатических констант
организма.
Слайд 50
Величина рср в большом круге кровообращения составляет приблизительно 100 мм
рт. ст. (13,3 кПа).
В малом круге рср = 15
мм рт. ст. (2 кПа), т. е. примерно в 6 раз меньше, чем в большом.
Слайд 51
Поскольку Vc обоих желудочков одинаков, а давление, против которого они
совершают работу, имеет шестикратное различие, то и статический компонент работы
левого желудочка приблизительно в 6 раз больше:Aст ЛЖ = 13,3.103 Па . 70.10-6 м3 = 0,9 Дж;
Аст ПЖ ~ 0,15 Дж.
Слайд 52
Кинетический компонент работы сердца определяется по формуле:
где ρ - плотность
крови (примерно 103 кг.м-3);
v - скорость кровотока в магистральном
артериальном стволе (в среднем 0,7 м.с-1).Слайд 53
Следовательно, Аk = 103 кг. м-3. 70.10-6 м3. 0,49 м2.
c-2 / 2= 0,02 Дж.
В целом работа левого желудочка за
одно сокращение в условиях покоя составляет около 1 Дж, а правого — менее 0,2 Дж, причем статический компонент доминирует, достигая 98% всей работы, тогда как на долю кинетического компонента приходится всего 2%. Средняя мощность миокарда поддерживается на уровне 1 Вт.
Слайд 54
Поэтому при физических и психических нагрузках вклад кинетического компонента в
работу сердца становится весомее (до 30% всей работы), чем в
покое.Например, при выполнении тяжелой физической работы тренированным человеком его рср достигает 16 кПа, Vc = 200 мл, и V = 3 м.с-1 .
Тогда работа левого желудочка достигает
А = 4,1 Дж.
Средняя мощность возрастает до 8,2 Вт.
Слайд 55
6. Биофизические особенности аорты. Пульсовая волна
Среди артерий эластического типа важнейшую
роль играет грудной отдел аорты.
С ним главным образом связана
основная функция сосудов этого типа — обеcпечение непрерывности кровотока. Слайд 56
Аст миокарда затрачивается на растяжение стенок артерий (прежде всего, грудного
отдела аорты).
Накопив энергию во время систолы, аортальная стенка отдает
ее крови в диастолу, когда сердце пребывает в расслабленном состоянии и не поставляет кровь в сосудистое русло. Благодаря упругости артерий эластического типа кровь не останавливается и в диастолу сердца, когда потенциальная энергия растянутой стенки артерии эластического типа преобразуется в кинетическую энергию крови.
Слайд 57
Упругость аортальной стенки обусловливает еще одно важное явление - возникновение
и распространение пульсовой волны по стенке артерий.
Дело в том,
что Fynp , развивающаяся при растяжении аорты, направлена не строго перпендикулярно к оси сосуда и может быть разложена на нормальную и тангенциальную составляющие.Слайд 59
Непрерывность кровотока обеспечивается первой из них, тогда как вторая
является источником артериального импульса, под которым понимают упругие колебания артериальной
стенки.Слайд 60
Пульсовая волна распространяется от места своего возникновения до капилляров, где
затухает. Скорость ее распространения (VП) можно рассчитать по формуле:
где Е
- модуль Юнга сосудистой стенки; b - ее толщина; r - радиус сосуда; ρ - плотность крови.Слайд 61
Общую характеристику пульсовой волны врач получает при пальпации артерии, но
более полные сведения дает регистрация кривой артериального пульса, которая называется
сфигмограммой.Слайд 62
Записав сфигмограммы в двух точках артериальной магистрали и измерив сдвиг
фазы между ними, можно определить скорость пульсовой волны в стенках
исследуемых артерий и по ней судить об их модуле Юнга.Скорость пульсовой волны в аорте составляет 4-6 м/с, а в лучевой артерии
8-12 м/с.
Слайд 63
С возрастом скорость пульсовой волны увеличивается.
Чем выше упругость артериальной
стенки, тем больше амплитуда колебаний кровяного давления в аорте и
крупных артериях.Высокоамплитудные колебания КД создают дополнительную нагрузку на сердце и усиливают деформацию сосудистых стенок.
Слайд 64
7. Биофизические особенности артериол большого круга кровообращения
Артериолы – предкапиллярные артерии.
Это
мелкие сосуды диаметром от 100 до 50 мкм.
Обладают гладкомышечной стенкой,
т.е. относятся к артериям мышечного типа.Слайд 66
Из-за малого радиуса артериолы обладают наибольшим гемодинамическим сопротивлением.
Радиус капилляров ещё
меньше (примерно, в 2,5 раза), длина капилляра меньше, а вязкость
крови в капиллярах больше. Если учесть всё это, то оказывается, что Rгд одного капилляра в 40-60 раз больше, чем у артериолы.Слайд 67
Но каждая артериола снабжает кровью около 100 капилляров, соединённых параллельно.
При этом общее сопротивление всех капилляров, отходящих от одной артериолы,
будет равно Rк/n, где Rк - сопротивление одного капилляра, а n - число капилляров. Поэтому гемодинамическое сопротивление всех капилляров составляет 0,4 - 0,6 от Rгд артериол.
Слайд 69
Так как разность давлений (падение давления) на участке, то есть
величина
р1 – р2, прямо пропорциональна гемодинамическому сопротивлению, наибольшее падение
давления происходит именно в артериолах.Это имеет ключевое значение для регуляции кровяного давления.
Слайд 70
В стенках мелких артерий (и особенно – артериол) находится много
мышечных волокон. Если артериальное кровяное давление (АКД) уменьшается, специальные рецепторы
сигнализируют об этом нервным узлам, расположенным в стенках сосудов.Оттуда поступают нервные импульсы к мышечным волокнам артериол, волокна сокращаются, и диаметры артериол уменьшаются.
Слайд 71
В результате растёт гемодинамическое сопротивление и, соответственно, повышается давление крови
в крупных артериях.
При увеличении АКД всё происходит в обратном
порядке. Таким образом, у здорового человека АКД достаточно точно поддерживается постоянным.
Слайд 72
Важно отметить, что во всех названных случаях диаметр артериол меняется
относительно мало.
Например, чтобы давление уменьшилось со 130 мм до
120 мм, достаточно увеличения диаметра артериолы всего на 8%. Если наблюдать в микроскоп, то такое увеличение размера сосуда почти незаметно.
Слайд 73
Таким образом, артерии мышечного типа, особенно артериолы большого круга кровообращения,
являются резистивными сосудами.
Они обеспечивают сопротивление работе сердца, что создает
«подпор» в системе кровообращения, проявляющийся в наличии кровяного давления. Слайд 74
Кроме того, еще И.М. Сеченов называл артериолы «сосудистыми кранами»:
они
распределяют кровь между потребителями – различными капиллярами.
Слайд 75
8. Транспорт веществ через стенку капилляра
Капилляры представляют собой тончайшие сосуды
диаметром 5—7 мкм, длиной 0,5—1,1 мм.
Эти сосуды пролегают в
межклеточных пространствах, тесно соприкасаясь с клетками органов и тканей организма. Суммарная длина всех капилляров тела человека составляет около 100 000 км, т. е. нить, которой можно было бы 3 раза опоясать земной шар по экватору.
Слайд 76
Физиологическое значение капилляров состоит в том, что через их стенки
осуществляется обмен веществ между кровью и тканями.
Стенки капилляров образованы
только одним слоем клеток эндотелия, снаружи которого находится тонкая соединительнотканная базальная мембрана. Слайд 77
Большое значение в обмене веществ между кровью и тканями имеет
фильтрация, основанная на градиенте давления жидкости.
Можно рассчитать силы фильтрации в
артериальном конце капилляра, как и силы обратного транспорта в его венозном конце.Слайд 78
Так, гидростатическое давление в артериальном конце капилляра в среднем составляет
34 мм. рт. ст.
Способствует фильтрации также онкотическое давление межтканевого
пространства, равное 3 мм. рт. ст. Следовательно, давление, способствующее фильтрации, составит: 34 + 3 = 37 мм. рт. ст.
Слайд 79
Вследствие фильтрации содержимое плазмы крови поступает в межтканевое пространство, где
происходит обмен с клетками (необходимые для жизнедеятельности вещества поступают в
клетки, а из последних выделяются продукты метаболизма).В венозном конце капилляра в результате обратного транспорта жидкость возвращается обратно в кровь, ее поступление зависит от тех же самых факторов, обеспечивающих фильтрацию.
Слайд 80
Факторы, обусловливающие обратный транспорт, составляют:
Онкотическое давление белков плазмы крови
- 23 мм. рт. ст.,
Гидростатическое давление межтканевого пространства -
4 мм. рт. ст.Итого - 27 мм рт. ст.
Слайд 81
Факторы, противодействующие обратному транспорту:
Гидростатическое давление крови - 18 мм.
рт. ст. ;
Онкотическое давление белков межтканевого пространства - 3
мм. рт. ст., Итого - 21 мм. рт. ст. Слайд 83
Подсчитано, что за один час фильтруется около 14 мл жидкости,
в то время, как обратному транспорту подвергается 12 мл.
Оставшаяся
жидкость (14 - 12 = 2 мл) возвращается в сосудистую систему посредством лимфатической системы.Слайд 84
9. Движение крови в венах
Движение крови в венах обеспечивает наполнение
полостей сердца во время диастолы.
Ввиду небольшой толщины мышечного слоя
стенки вен гораздо более растяжимы, чем стенки артерий, поэтому в венах может скапливаться большое количество крови.Слайд 85
Даже если давление в венозной системе повысится всего на несколько
миллиметров, объем крови в венах увеличится в 2—3 раза, а
при повышении давления в венах на 10 мм рт.ст. вместимость венозной системы возрастет в 6 раз.Вместимость вен может также изменяться при сокращении или расслаблении гладкой мускулатуры венозной стенки.