Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Большие списки
Содержание
- 1. Большие списки
- 2. Находим в массиве наибольший элемент и помещаем
- 3. Находим в массиве второй по величине элемент
- 4. К-ый элементДалее процесс повторяется до расположения к-го по величине элемента на нужном местеК-ый элемент
- 5. В массиве задаем опорный элемент “P1”Просматриваем
- 6. В оставшейся части массива задаем опорный элемент
- 7. Продолжаем этот процесс. Возможны два варианта завершения:На
- 8. Алгоритмы сортировкиЕсть последовательность ,
- 9. Возможна ситуация, когда элементы состоят из нескольких
- 10. Критерии эффективности работы алгоритмовВремя сортировки - основной
- 11. Устойчивость - устойчивая сортировка не меняет взаимного
- 12. Естественность поведения - эффективность метода при обработке
- 13. Сравнение времени сортировок коричневая линия: сортировка
- 14. Быстрая сортировка Метод основан на подходе "разделяй-и-властвуй". Общая
- 15. Разделение массиваНа входе массив a[0]...a[N] и опорный
- 16. Исходный массивПервый обменВторой обмен653918457437192436539184574371924365391849743715243
- 17. Третий обменЧетвертый обменКонечный результат653918797434152431539687974341524315369879743415243
- 18. Конечный результатРазделённые массивыДля разделённых массивов процедура повторяется1536987974341524315369879743415243Первый массивВторой массив
- 19. Общее быстродействие метода - хорошее. Метод неустойчив.
- 20. Сортировка слияниемСортировка слиянием также построена на принципе
- 21. Рекурсивный алгоритм обходит получившееся дерево слияния в
- 22. Исходный массивПервый проход – парыВторой проход – четвёрки3728461537824615
- 23. Третий проход – восьмёркиПроцесс слияния в буфер2378145614562378
- 24. Сортировку слиянием используют для упорядочения массивов, лишь
- 25. Скачать презентанцию
Находим в массиве наибольший элемент и помещаем его в буферСдвигаем правую часть массива на одну ячейку влевоНаибольший элемент из буфера перемещаем в конец массива
Слайды и текст этой презентации
Слайд 1Большие списки
Очень большие списки можно разбить на подсписки и
выбрать один подсписок, в котором содержатся интересующие нас элементы.
Слайд 2Находим в массиве наибольший элемент и помещаем его в буфер
Сдвигаем
правую часть массива на одну ячейку влево
Наибольший элемент из буфера
перемещаем в конец массива
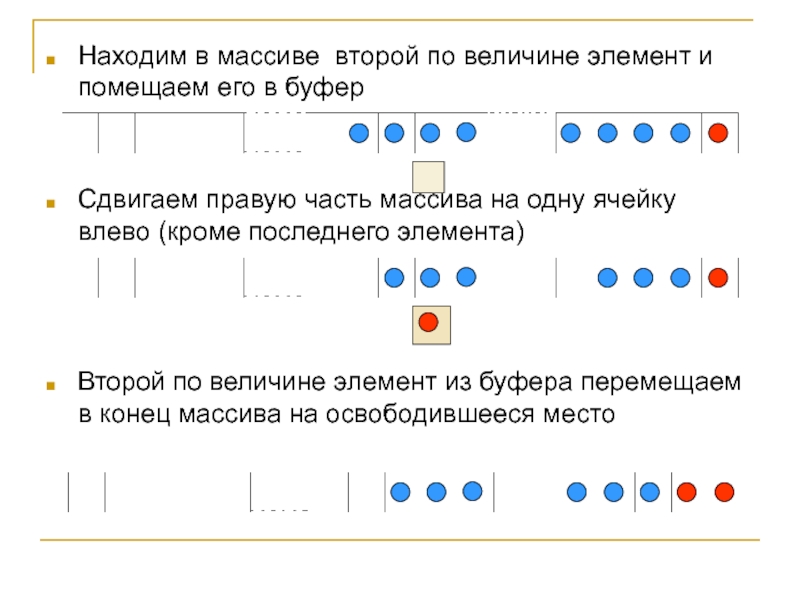
Слайд 3Находим в массиве второй по величине элемент и помещаем его
в буфер
Сдвигаем правую часть массива на одну ячейку влево (кроме
последнего элемента)Второй по величине элемент из буфера перемещаем в конец массива на освободившееся место
Слайд 4К-ый элемент
Далее процесс повторяется до расположения к-го по величине элемента
на нужном месте
К-ый элемент
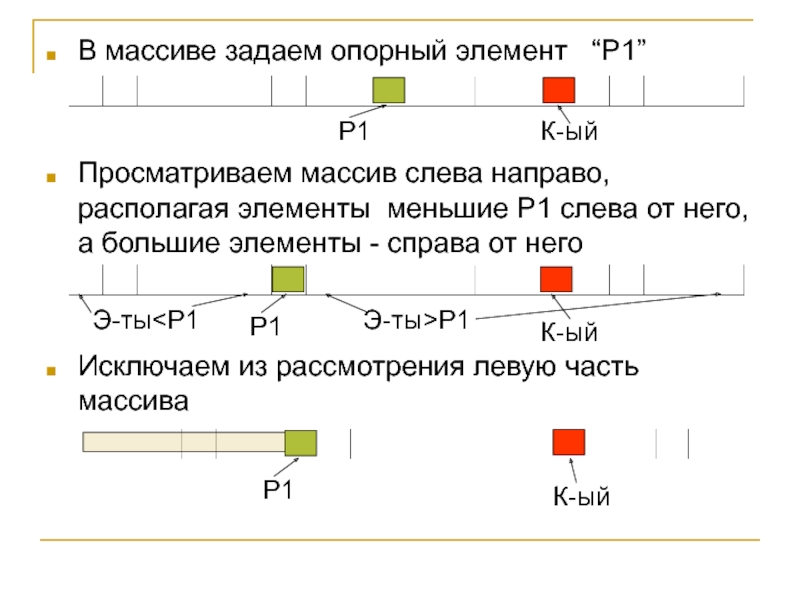
Слайд 5В массиве задаем опорный элемент “P1”
Просматриваем массив слева направо,
располагая элементы меньшие P1 слева от него, а большие элементы
- справа от негоИсключаем из рассмотрения левую часть массива
P1
К-ый
P1
К-ый
P1
К-ый
Э-ты Э-ты>P1
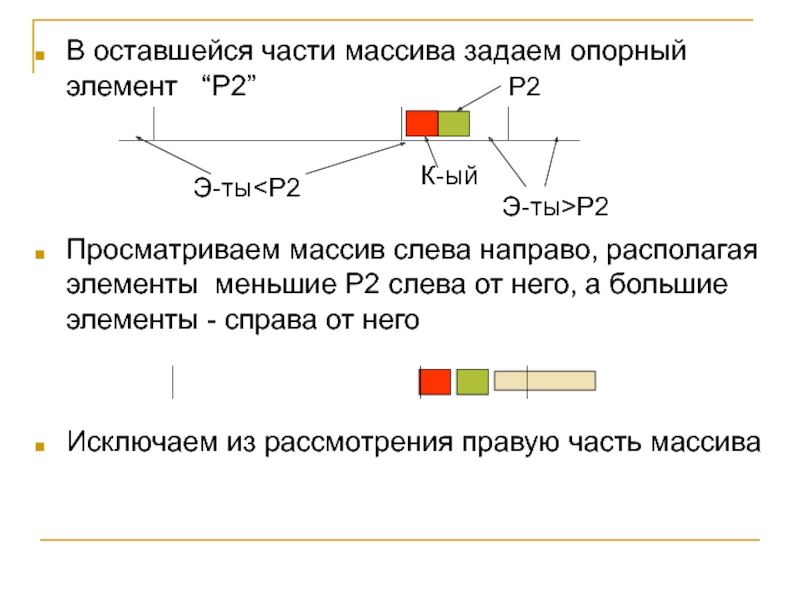
Слайд 6В оставшейся части массива задаем опорный элемент “P2”
Просматриваем массив
слева направо, располагая элементы меньшие P2 слева от него, а
большие элементы - справа от негоИсключаем из рассмотрения правую часть массива
P2
К-ый
Э-ты Э-ты>P2
Слайд 7
Продолжаем этот процесс.
Возможны два варианта завершения:
На очередной итерации опорный
элемент Pi располагается на К-ой позиции.
Процесс сокращения интервала идет до
логического конца – остается подинтервал из двух элементов, один из которых располагается на К-ой позиции.Слайд 8Алгоритмы сортировки
Есть последовательность , ...
и функция сравнения, которая
на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие:
для всех i от 0 до n.
Слайд 9Возможна ситуация, когда элементы состоят из нескольких полей:
Если значение функции
сравнения зависит только от поля x , то x называют
ключом, по которому производится сортировка.На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.
x
y
Слайд 10Критерии эффективности работы алгоритмов
Время сортировки - основной параметр, характеризующий быстродействие
алгоритма.
Память - ряд алгоритмов требует выделения дополнительной памяти под временное
хранение данных. При оценке используемой памяти не учитывается место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы. Слайд 11Устойчивость - устойчивая сортировка не меняет взаимного расположения равных элементов.
Расположение дополнительных полей "a", "b", "c" осталось прежним
Взаимное расположение
равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось Слайд 12
Естественность поведения - эффективность метода при обработке уже отсортированных, или
частично отсортированных данных.
Алгоритм ведет себя естественно, если учитывает эту
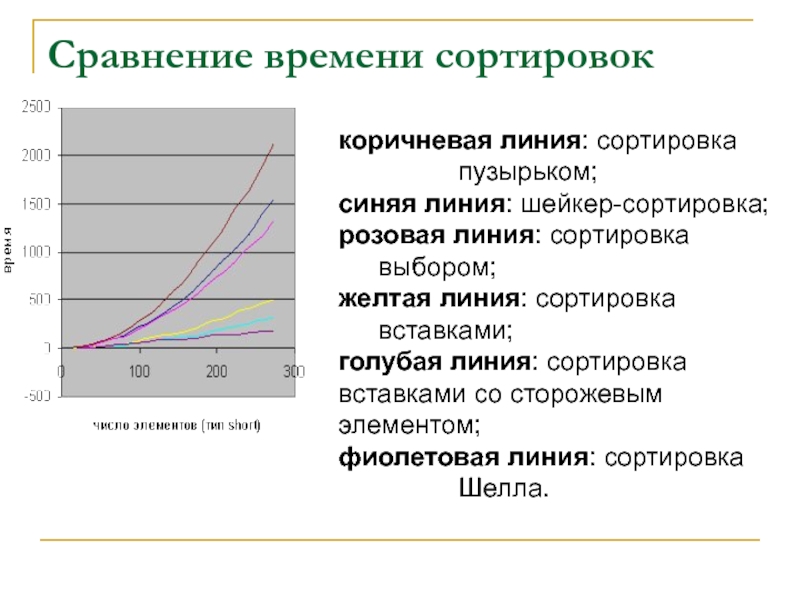
характеристику входной последовательности. Слайд 13Сравнение времени сортировок
коричневая линия: сортировка пузырьком;
синяя линия: шейкер-сортировка;
розовая линия: сортировка выбором;
желтая линия: сортировка
вставками; голубая линия: сортировка вставками со сторожевым элементом;
фиолетовая линия: сортировка Шелла.
Слайд 14Быстрая сортировка
Метод основан на подходе "разделяй-и-властвуй". Общая схема такова:
из
массива выбирается некоторый опорный элемент a[i],
запускается процедура разделения массива,
которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо, теперь массив состоит из двух подмножеств, причем левое меньше (либо равно) правого,
для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.
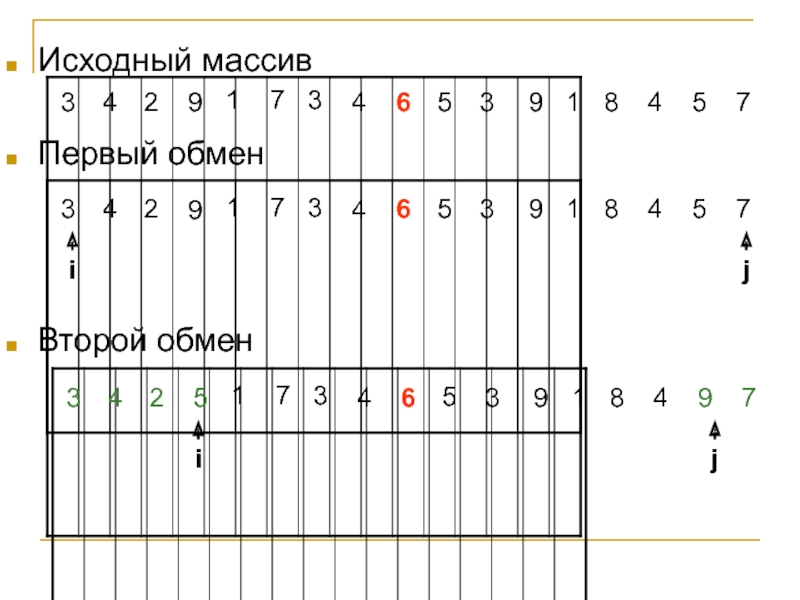
Слайд 15 Разделение массива
На входе массив a[0]...a[N] и опорный элемент p, по
которому будет производиться разделение.
Введем два указателя: i и j.
В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.
Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i, j по тем же правилам...
Повторяем шаг 3, пока i <= j.
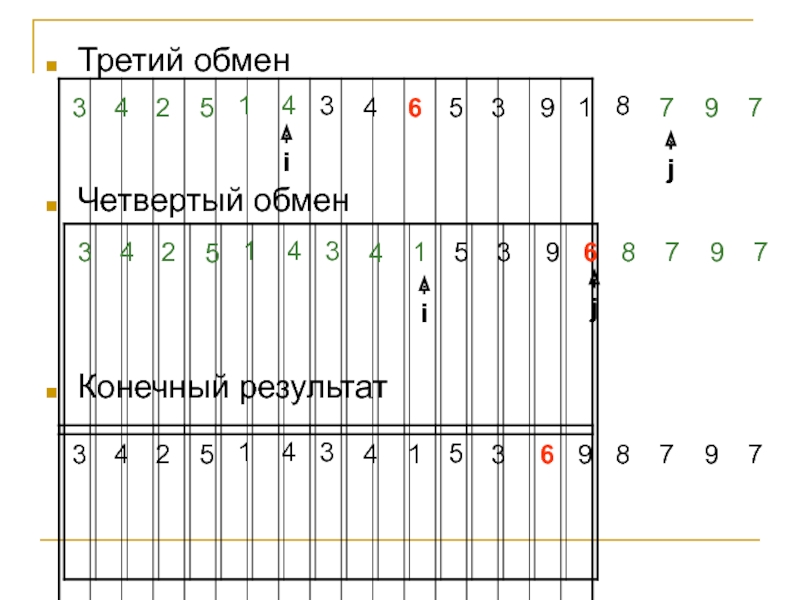
Слайд 17Третий обмен
Четвертый обмен
Конечный результат
6
5
3
9
1
8
7
9
7
4
3
4
1
5
2
4
3
1
5
3
9
6
8
7
9
7
4
3
4
1
5
2
4
3
1
5
3
6
9
8
7
9
7
4
3
4
1
5
2
4
3
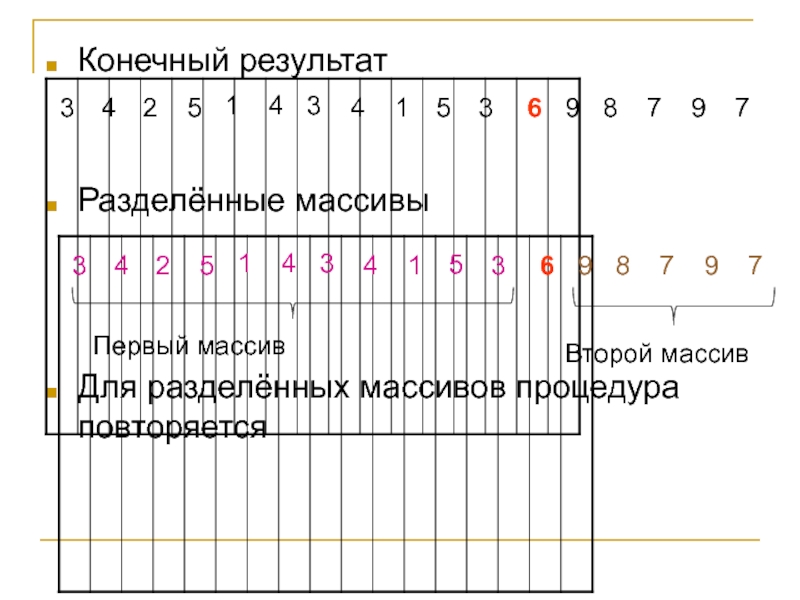
Слайд 18Конечный результат
Разделённые массивы
Для разделённых массивов процедура повторяется
1
5
3
6
9
8
7
9
7
4
3
4
1
5
2
4
3
1
5
3
6
9
8
7
9
7
4
3
4
1
5
2
4
3
Первый массив
Второй массив
Слайд 19Общее быстродействие метода - хорошее.
Метод неустойчив.
Поведение довольно естественно,
если учесть, что при частичной упорядоченности повышаются шансы разделения массива
на более равные части.Сортировка использует дополнительную память, так как данные о рекурсивных подвызовах каждый раз запоминать.
Слайд 20Сортировка слиянием
Сортировка слиянием также построена на принципе "разделяй-и-властвуй", однако реализует
его несколько по-другому, нежели быстрая сортировка.
Вместо разделения по опорному
элементу массив просто делится пополам.Слайд 21
Рекурсивный алгоритм обходит получившееся дерево слияния в прямом порядке. Каждый
уровень представляет собой проход сортировки слияния - операцию, полностью переписывающую
массив.Деление происходит до массива из единственного элемента. Такой массив можно считать упорядоченным.
Один из способов состоит в слиянии двух упорядоченных последовательностей при помощи вспомогательного буфера, равного по размеру общему количеству имеющихся в них элементов. Элементы последовательностей будут перемещаться в этот буфер по одному за шаг.
Слайд 24
Сортировку слиянием используют для упорядочения массивов, лишь если требуется устойчивость
метода (которой нет у быстрой сортировки).
Сортировка слиянием является одним из
наиболее эффективных методов для списков, когда есть лишь последовательный доступ к элементам.Несмотря на хорошее общее быстродействие и учитывая отсутствие "худшего случая", у сортировки слиянием есть и серьезный минус: она требует дополнительную память.









![Большие списки Разделение массиваНа входе массив a[0]...a[N] и опорный элемент p, по которому Разделение массиваНа входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение. Введем два указателя:](/img/thumbs/fc21b89cfe7995e6a591b7490b7abbbe-800x.jpg)