Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числа и векторы
Содержание
- 1. Числа и векторы
- 2. Содержание лекции 1. ПО и программирование. Парадигмы
- 3. Программное обеспечение Программное обеспечение принято по
- 4. Программное обеспечение Прикладное ПО
- 5. Программное обеспечение Прикладное ПО
- 6. Программное обеспечение Прикладное ПО
- 7. Программное обеспечение Прикладное ПО
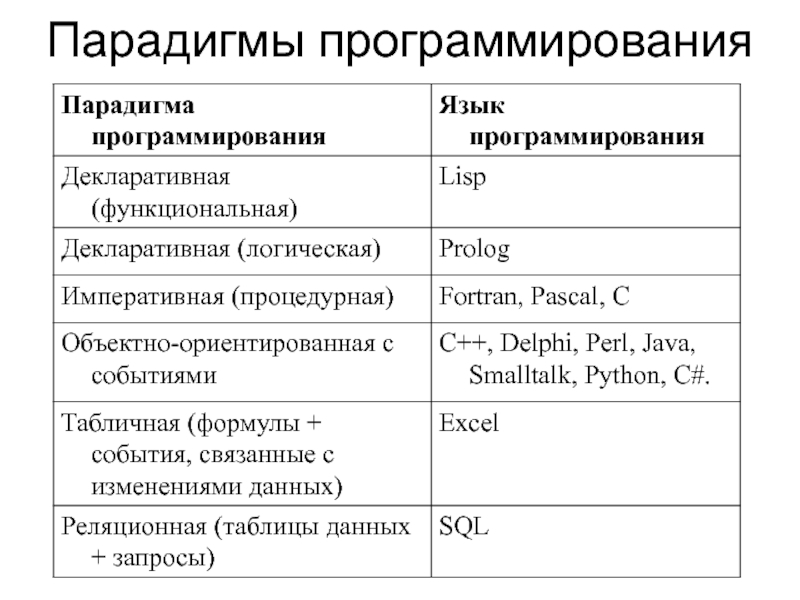
- 8. Парадигмы программирования Агентно-ориентированнаяКомпонентно-ориентированнаяКонкатенативнаяДекларативнаяДекларативная (контрастирует с Императивной) ОграничениямиФункциональнаяПотоком данных Таблично-ориентированная (электронные таблицы)РеактивнаяЛогическаяСобытийно-ориентированная Сервис-ориентированнаяКомбинаторнаяИмперативнаяИмперативная (контрастирует с Декларативной) Процедурная
- 9. Парадигмы программирования Предметно-ориентированнаяМетапрограммирование Автоматизация процесса программированияОбобщённое
- 10. Парадигмы программирования Декларативное программирование 1. Программа
- 11. Парадигмы программирования Императивное программирование — это парадигма
- 12. Парадигмы программирования Функциональное программирование — парадигма программирования —
- 13. Парадигмы программирования Событийно-ориентированное программирование (англ. event-driven programming;
- 14. Парадигмы программирования Процедурное (императивное) программирование является
- 15. Парадигмы программирования Объектно-ориентированное, или объектное, программирование
- 16. Парадигмы программирования
- 17. Парадигмы программирования Программы = Алгоритмы + структуры данных (Н. Вирт)Паскаль и Вирт
- 18. Парадигмы программирования Программы = Алгоритмы +
- 19. Парадигмы программирования Программы = Алгоритмы +
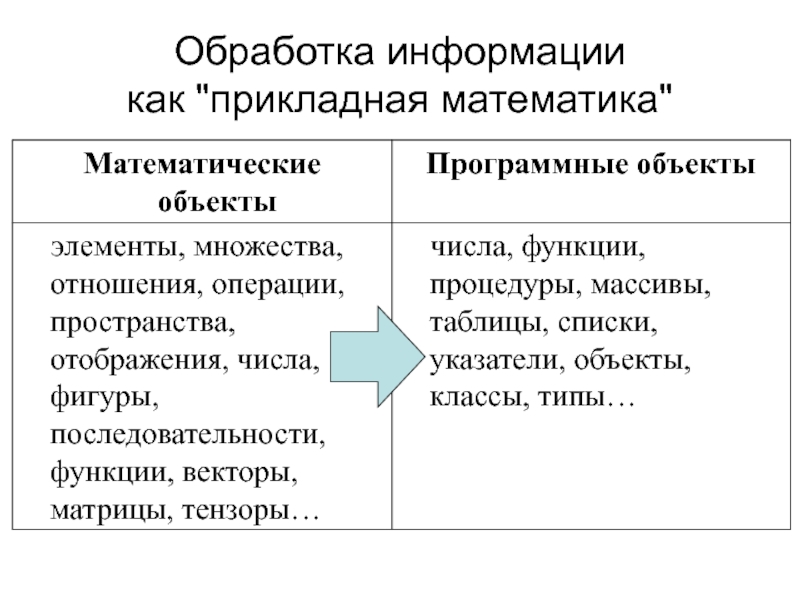
- 20. Обработка информации как "прикладная математика"
- 21. Числа - базовый тип данных в прикладной
- 22. Задачи и числа. Решение уравненийОктонионыДля решения арифметических уравнений видаx = a +by = ab
- 23. Задачи и числа. Решение уравненийОктонионыДля решения арифметических
- 24. Задачи и числа. Решение уравненийОктонионыДля решения арифметических уравнений видаb = ax ⇒ x = b/a
- 25. Задачи и числа. Решение уравненийОктонионыДля решения алгебраических уравнений видаb = axn ⇒ x = n√ (b/a)
- 26. Задачи и числа. Решение уравненийОктонионыДля решения любых
- 27. Дальнейшее расширение понятия "числа"ОктонионыПодробнее см.
- 28. Комплексные числа и операции с точками на
- 29. Комплексные числа и операции с точками на
- 30. Комплексные числа и операции с точками на
- 31. Кватернионы и операции с точками пространства Кватернион
- 32. Кватернионы и операции с точками пространства Кватернионы
- 33. Октонионы и операции с точками пространства Октонион
- 34. Других чисел нет!
- 35. произведение сумм четырёх квадратов является суммой четырёх
- 36. Других чисел нет!Тождество восьми квадратов — математическая теорема о том, что
- 37. А другие пространства есть… Векторы и "Векторы" ВекторВекторное
- 38. А другие пространства есть… МатрицыМатрица — математический объект,
- 39. Задачи и матрицы. Системы линейных уравненийСистему из
- 40. В частном случае, когда рассматриваются линейные преобразования
- 41. Представление чисел в компьютерных системах Подробнее см.
- 42. Представление чисел и других данных в компьютерных
- 43. Натуральные двоичные числа Преобразование десятичных чисел в
- 44. Информативность натуральных двоичных чисел Вопрос: Число больше
- 45. Представление целых чисел в ЭВМ Дополнительный код
- 46. Представление дробных чисел в ЭВМ Число с
- 47. Представление действительных чисел Плавающая запятая — форма представления
- 48. Типы данных Подробнее см.Простые. Перечислимый тип. Может
- 49. Типы данных Подробнее см.Составные (сложные). МассивМассив. Является
- 50. Типы данных Подробнее см.Структурные типы данных Регулярные
- 51. Типы данных. Массив Индексный массив — именованный
- 52. Типы данных. Структура Структура — конструкция большинства языков
- 53. Типы данных. Список Связный список — структура данных,
- 54. Типы данных. Динамические списки типа "стек" и
- 55. Типы данных. Динамические списки типа "стек" и
- 56. Типы данных. Графы (модели) Граф — это совокупность
- 57. Типы данных. Графы (модели) Неориентированный граф G —
- 58. Типы данных. Графы (модели) Ориентированный граф (сокращённо
- 59. Типы данных. Графы (модели) Граф называется:связным, если
- 60. Типы данных. Графы: деревья Дерево — является связанным
- 61. Типы данных. Графы: Деревья, Сети Подробнее см.
- 62. Типы данных. Таблицы. Базы данных Подробнее см.Кортежи.
- 63. Типы данных. Кодирование данных Подробнее см.Структурные типы
- 64. Типы данных. Цифровое изображение Лабораторная система обработки
- 65. Компьютерное зрение как типовая область компьютерной обработки
- 66. Компьютерное зрение как обобщение школьной геометрии
- 67. Компьютерное зрение как школьная геометрия++ Отличия КЗ
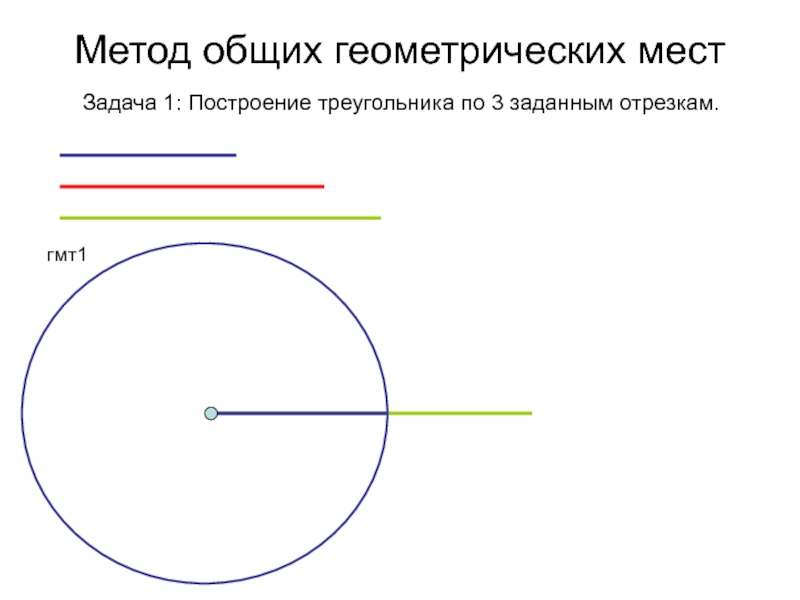
- 68. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.
- 69. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1
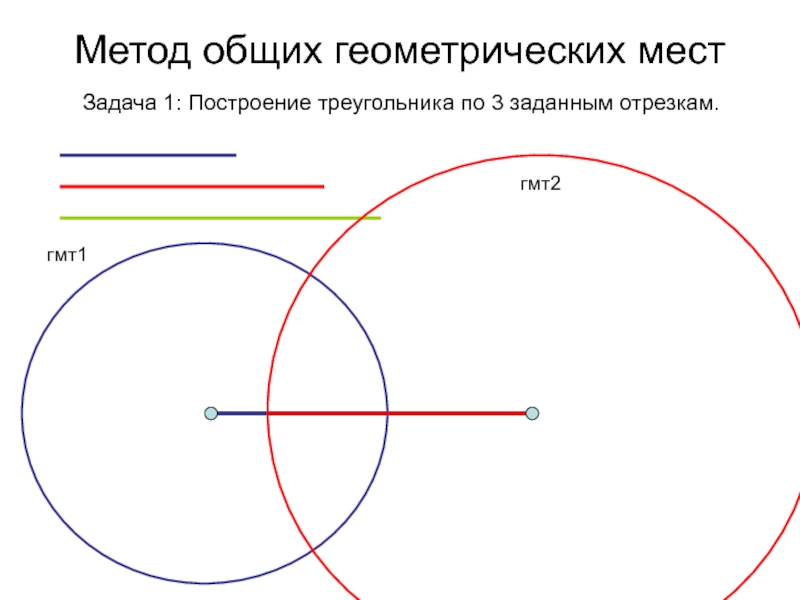
- 70. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1гмт2
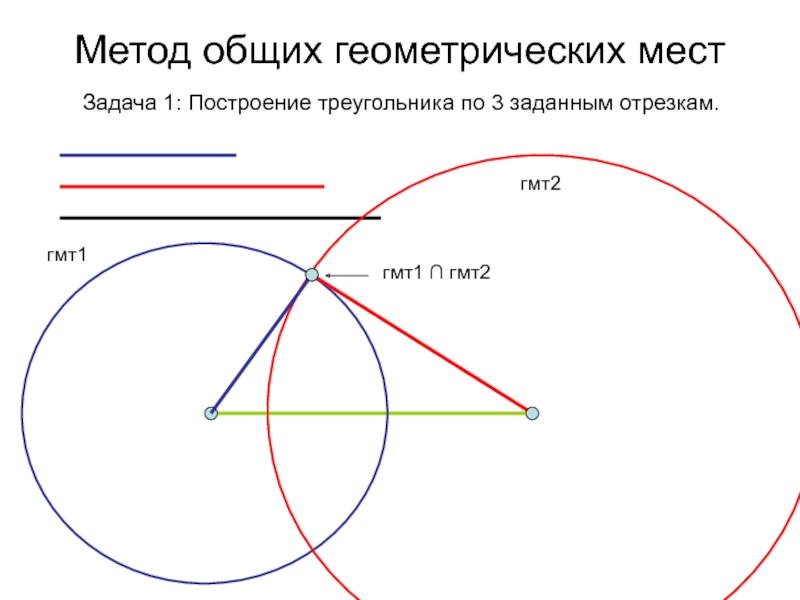
- 71. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1гмт2гмт1 ∩ гмт2
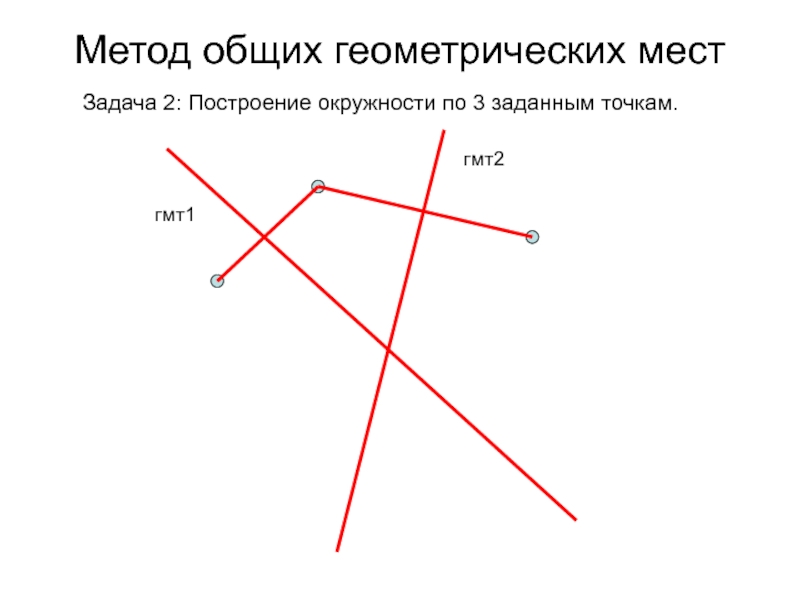
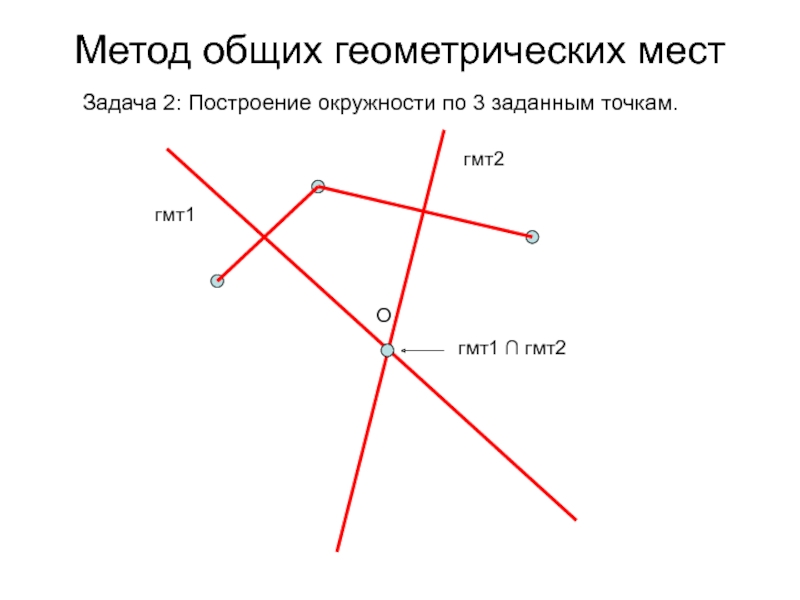
- 72. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.
- 73. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1
- 74. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2
- 75. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2O
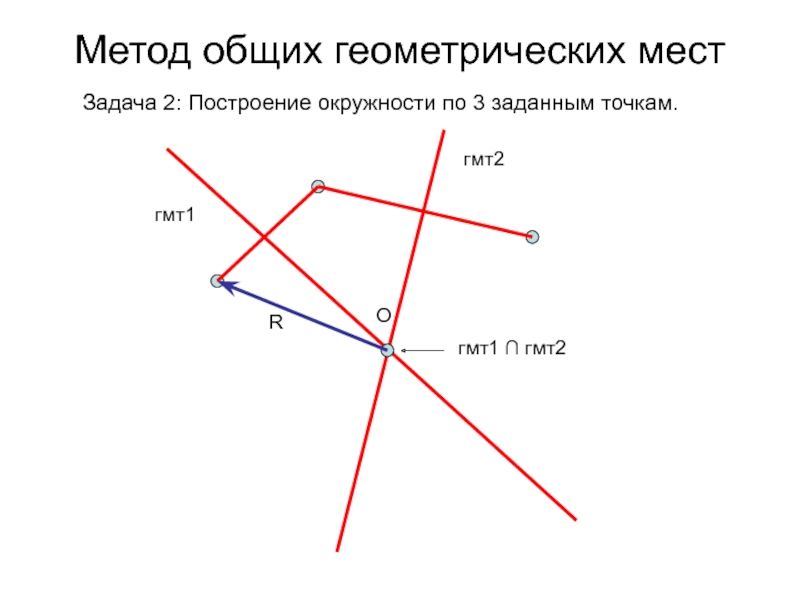
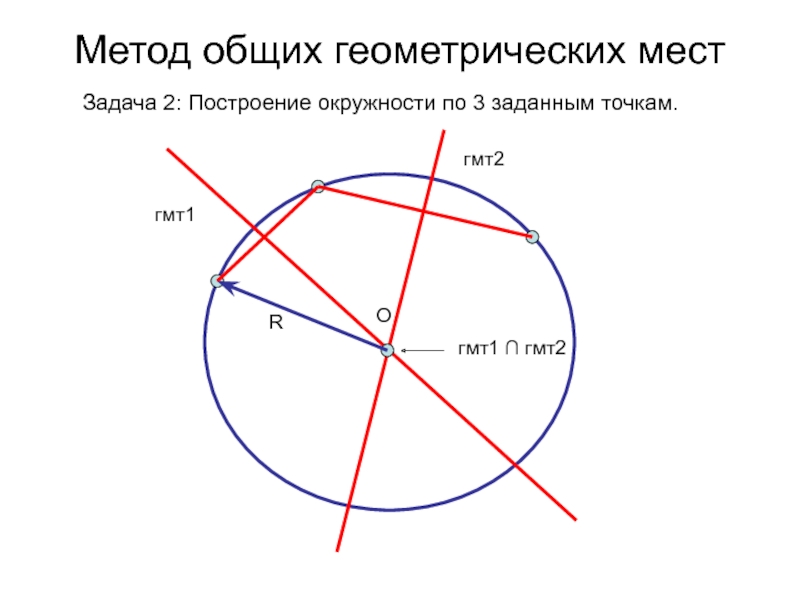
- 76. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2RO
- 77. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2RO
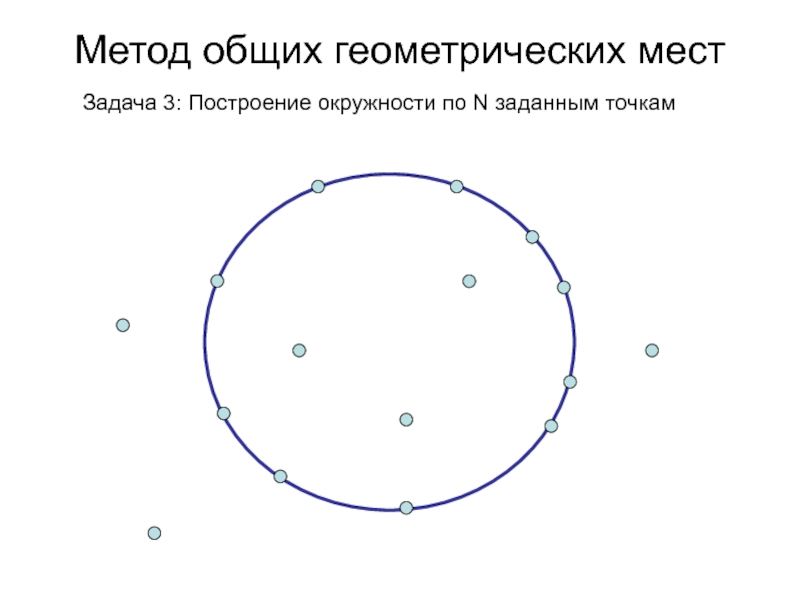
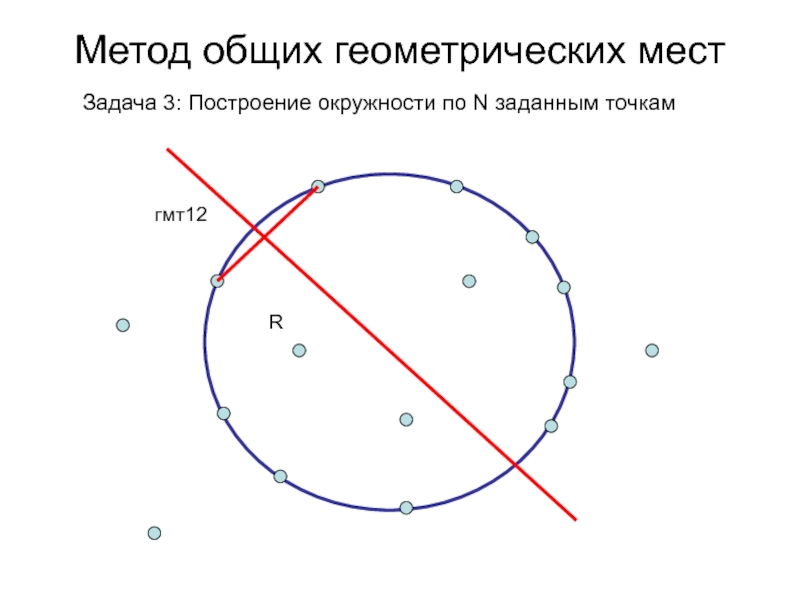
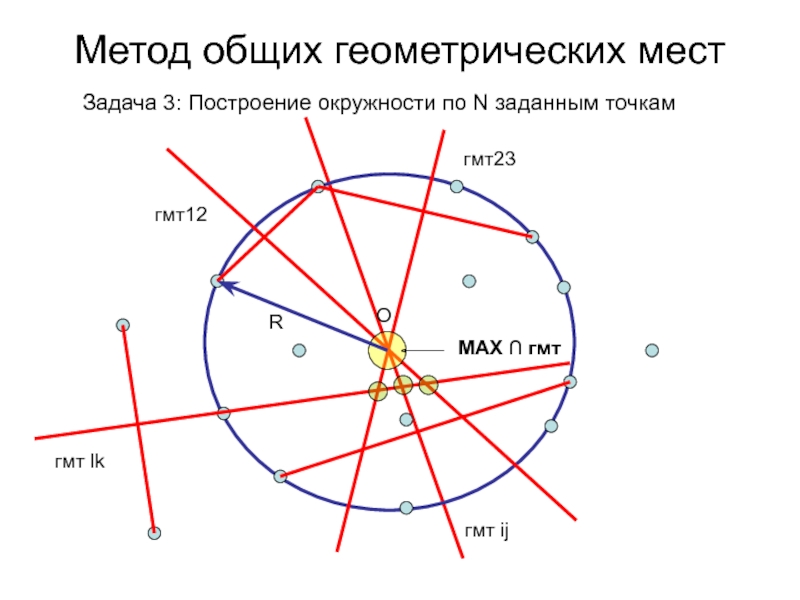
- 78. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкам
- 79. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкам
- 80. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12R
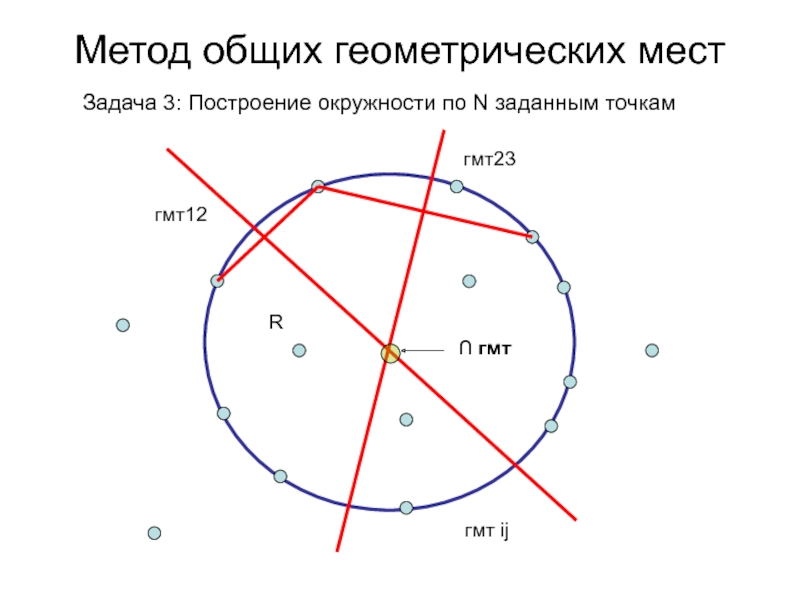
- 81. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23∩ гмтRгмт ij
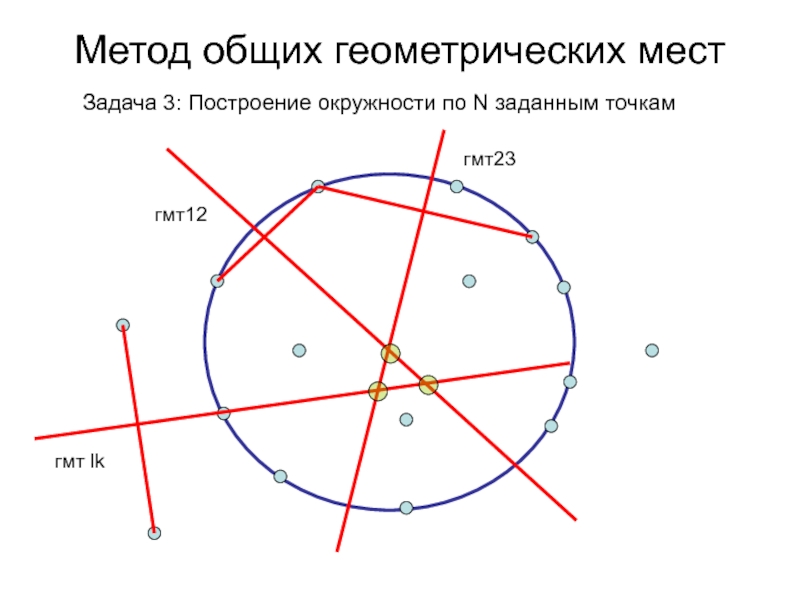
- 82. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23гмт lk
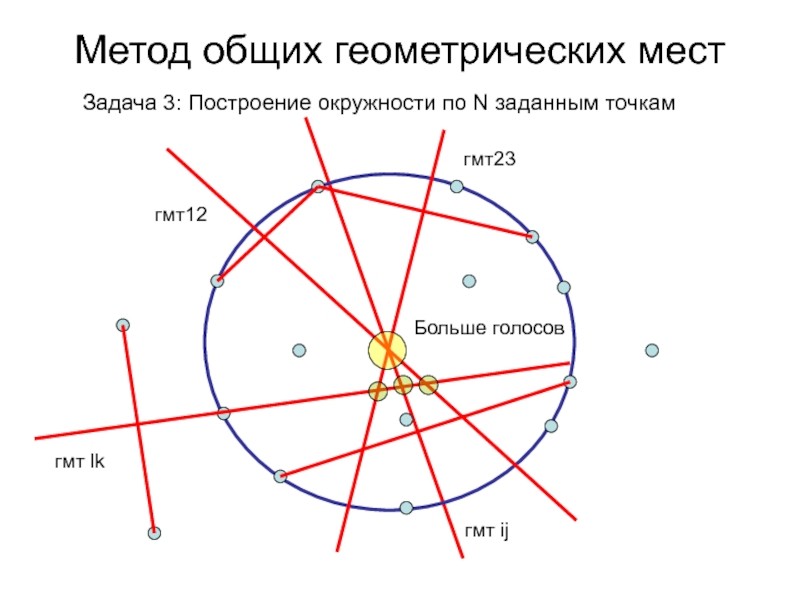
- 83. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23гмт ijгмт lkБольше голосов
- 84. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23MAX ∩ гмтROгмт ijгмт lk
- 85. Области применения и типовые примеры практических систем компьютерного и машинного зрения. Примеры приложений
- 86. Задачи и методы компьютерной обработки информации Содержание учебного курса
- 87. Возможные темы курсовых Программа учебного курса
- 88. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1КОМПЬЮТЕРНЫЕ МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ
Лекция 02 (С)
Методы компьютерного представления информации.
Цифровое изображение и компьютерное зрение.
Слайд 2Содержание лекции
1. ПО и программирование. Парадигмы программирования. Роль способа
представления данных.
2. Методы компьютерного представления и передачи информации.
3. Цифровое изображение.
Сжатие видеоинформации.4. Компьютерное зрение. Области приложения и примеры систем.
5. Возможные темы курсовых работ.
Слайд 3Программное обеспечение
Программное обеспечение принято по назначению подразделять на
системноеПрограммное обеспечение принято по назначению подразделять на системное, прикладноеПрограммное обеспечение
принято по назначению подразделять на системное, прикладное и инструментальное.Системное ПО
Инструментальное ПО
Слайд 8Парадигмы программирования
Агентно-ориентированная
Компонентно-ориентированная
Конкатенативная
ДекларативнаяДекларативная (контрастирует с Императивной)
Ограничениями
Функциональная
Потоком данных
Таблично-ориентированная (электронные
таблицы)
Реактивная
Логическая
Событийно-ориентированная
Сервис-ориентированная
Комбинаторная
ИмперативнаяИмперативная (контрастирует с Декларативной)
Процедурная
Слайд 9Парадигмы программирования
Предметно-ориентированная
Метапрограммирование
Автоматизация процесса программирования
Обобщённое программирование
Рефлексивно-ориентированная
Итерационная
Параллельная
Структурная
Модульная
Рекурсивная
Объектно-ориентированная
Автоматная
Разделение
ответственности:
Аспектно-ориентированная
Субъектно-ориентированная
Прототип-ориентированная
Слайд 10Парадигмы программирования
Декларативное программирование 1. Программа «декларативна», если она
описывает каково́ нечто, а не как его создать. Например, веб-страницы
на HTML декларативны, так как они описывают что должна содержать страница, а не как отображать страницу на экране. Этот подход отличается от языков императивного программирования, требующих от программиста указывать алгоритм для исполнения.Декларативное программирование 2. Программа «декларативна», если она написана на исключительно функциональном Программа «декларативна», если она написана на исключительно функциональном, логическом Программа «декларативна», если она написана на исключительно функциональном, логическом или языке программирования с ограничениями Программа «декларативна», если она написана на исключительно функциональном, логическом или языке программирования с ограничениями. Выражение «декларативный язык» иногда употребляется для описания всех таких языков программирования как группы, чтобы подчеркнуть их отличие от императивных языков.
Слайд 11Парадигмы программирования
Императивное программирование — это парадигма программирования — это парадигма
программирования, которая, в отличие от декларативного программирования — это парадигма программирования,
которая, в отличие от декларативного программирования, описывает процесс вычисления в виде инструкций — это парадигма программирования, которая, в отличие от декларативного программирования, описывает процесс вычисления в виде инструкций, изменяющих состояние программы. Императивная программа очень похожа на приказы, выражаемые повелительным наклонением в естественных языках — это парадигма программирования, которая, в отличие от декларативного программирования, описывает процесс вычисления в виде инструкций, изменяющих состояние программы. Императивная программа очень похожа на приказы, выражаемые повелительным наклонением в естественных языках, то есть это последовательность команд, которые должен выполнить компьютер.Императивные языки программирования противопоставляются функциональным противопоставляются функциональным и логическим противопоставляются функциональным и логическим языкам программирования. Функциональные языки, например, Haskell противопоставляются функциональным и логическим языкам программирования. Функциональные языки, например, Haskell, не представляют собой последовательность инструкций и не имеют глобального состояния. Логические языки программирования, такие как Prolog, обычно определяют что надо вычислить, а не как это надо делать.
Слайд 12Парадигмы программирования
Функциональное программирование — парадигма программирования — парадигма программирования, в
которой процесс вычисления — парадигма программирования, в которой процесс вычисления трактуется
как вычисление значений функций — парадигма программирования, в которой процесс вычисления трактуется как вычисление значений функций в математическом понимании последних (в отличие от функций как подпрограмм в процедурном программировании).Противопоставляется парадигме императивного программированияПротивопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состоянийПротивопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состояний (в значении, подобном таковому в теории автоматовПротивопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состояний (в значении, подобном таковому в теории автоматов). Функциональное программирование предполагает обходиться вычислением результатов функций от исходных данных и результатов других функций, и не предполагает явного хранения состояния программы. Соответственно, не предполагает оно и изменяемость этого состояния (в отличие от императивногоПротивопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состояний (в значении, подобном таковому в теории автоматов). Функциональное программирование предполагает обходиться вычислением результатов функций от исходных данных и результатов других функций, и не предполагает явного хранения состояния программы. Соответственно, не предполагает оно и изменяемость этого состояния (в отличие от императивного, где одной из базовых концепций является переменнаяПротивопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состояний (в значении, подобном таковому в теории автоматов). Функциональное программирование предполагает обходиться вычислением результатов функций от исходных данных и результатов других функций, и не предполагает явного хранения состояния программы. Соответственно, не предполагает оно и изменяемость этого состояния (в отличие от императивного, где одной из базовых концепций является переменная, хранящая своё значение и позволяющая менять его по мере выполнения алгоритма).
Слайд 13Парадигмы программирования
Событийно-ориентированное программирование (англ. event-driven programming; СОП) — парадигма программирования;
СОП) — парадигма программирования, в которой выполнение программы; СОП) — парадигма программирования,
в которой выполнение программы определяется событиями; СОП) — парадигма программирования, в которой выполнение программы определяется событиями — действиями пользователя (клавиатура, мышь), сообщениями других программ и потоков, событиями операционной системы (например, поступлением сетевого пакета).СОП можно также определить как способ построения компьютерной программы, при котором в коде (как правило, в головной функции программы) явным образом выделяется главный цикл приложения, тело которого состоит из двух частей: выборки события и обработки события.
Слайд 14Парадигмы программирования
Процедурное (императивное) программирование является отражением архитектуры является
отражением архитектуры традиционных ЭВМ является отражением архитектуры традиционных ЭВМ, которая
была предложена фон Нейманом является отражением архитектуры традиционных ЭВМ, которая была предложена фон Нейманом. Теоретической моделью процедурного программирования Машина Тьюринга. Выполнение программы сводится к последовательному выполнению операторов с целью преобразования исходного состояния памяти, то есть значений исходных данных, в заключительное, то есть в результаты. Таким образом, с точки зрения программиста имеются программа и память, причем первая последовательно обновляет содержимое последней.Процедурный язык программирования предоставляет возможность программисту определять каждый шаг в процессе решения задачи. Используя процедурный язык, программист определяет языковые конструкции для выполнения последовательности алгоритмических шагов.
Слайд 15Парадигмы программирования
Объектно-ориентированное, или объектное, программирование (ООП) — парадигма программирования,
программирование (ООП) — парадигма программирования, в которой основными концепциями, программирование (ООП) —
парадигма программирования, в которой основными концепциями являются понятия объектов, программирование (ООП) — парадигма программирования, в которой основными концепциями являются понятия объектов и классов.Объект — это сущность, которой можно посылать сообщения, и которая может на них реагировать, используя свои данные. Данные объекта скрыты от остальной программы. Сокрытие данных называется инкапсуляцией.
Класс описывает множество объектов одного типа. Новые классы (объекты) порождаются из прежних путем наследования описывает множество объектов одного типа. Новые классы (объекты) порождаются из прежних путем наследования их основных свойств. Полиморфизм классов дает возможность для объектов с одинаковой спецификацией иметь различную реализацию (классы-наследники изменяют одноименные свойства классов-предков).
Слайд 18Парадигмы программирования
Программы = Алгоритмы + структуры данных
Что
нужно помнить:
Разные способы представления одних и тех же данных связаны
с разными способами их обработки (разными алгоритмами).Для решения каждой конкретной задачи всегда найдется эффективный способ представления данных
Пример-задача. Как оптимальным образом представить целое число, чтобы компьютерная программа могла определить, делится оно нацело на 3? А на 9? А на 19? А на 21?
Подсказка: Пользоваться можно любыми элементарными функциями из школьной программы.
(Кнут Д.Э. Искусство программирования. В 3-х томах. М: Вильямс, 2007. 720 с., 832 с., 824 с.)
Слайд 19Парадигмы программирования
Программы = Алгоритмы + структуры данных
Пример-задача.
Как оптимальным образом представить целое число, чтобы компьютерная программа могла
определить, делится оно нацело на 3? А на 9? А на 19? А на 21?Подсказка: Пользоваться можно любыми элементарными функциями из школьной программы.
Ответ. Число N делится нацело на число K, если
Cos(2πK/N) = 1
(Кнут Д.Э. Искусство программирования. В 3-х томах. М: Вильямс, 2007. 720 с., 832 с., 824 с.)
Слайд 21Числа - базовый тип данных
в прикладной математике
Подробнее см.
Определение: "Число" это
такой математический объект, для которого определены 4 арифметических действия (+,-,×÷).
Основная
идея: Разные типы чисел, как и все другие типы данных, появлялись в связи с необходимостью решать разные типы прикладных задач. Слайд 22Задачи и числа.
Решение уравнений
Октонионы
Для решения арифметических уравнений вида
x = a
+b
y = ab
Слайд 23Задачи и числа.
Решение уравнений
Октонионы
Для решения арифметических уравнений вида
b = a
+ x ⇒ x = b – a
y = ab
Слайд 24Задачи и числа.
Решение уравнений
Октонионы
Для решения арифметических уравнений вида
b = ax
⇒ x = b/a
Слайд 25Задачи и числа.
Решение уравнений
Октонионы
Для решения алгебраических уравнений вида
b = axn
⇒ x = n√ (b/a)
Слайд 26Задачи и числа.
Решение уравнений
Октонионы
Для решения любых алгебраических уравнений:
c0 + c1x
+ c2x2 + c3x3 + …. = 0
⇒ x =
a + ib, где i = √-1.Слайд 28Комплексные числа и операции
с точками на плоскости
Действия над комплексными
числами
Сравнение
a + bi = c + di означает, что
a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).Сложение
(a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание
(a + bi) − (c + di) = (a − c) + (b − d)i.
Умножение
Деление
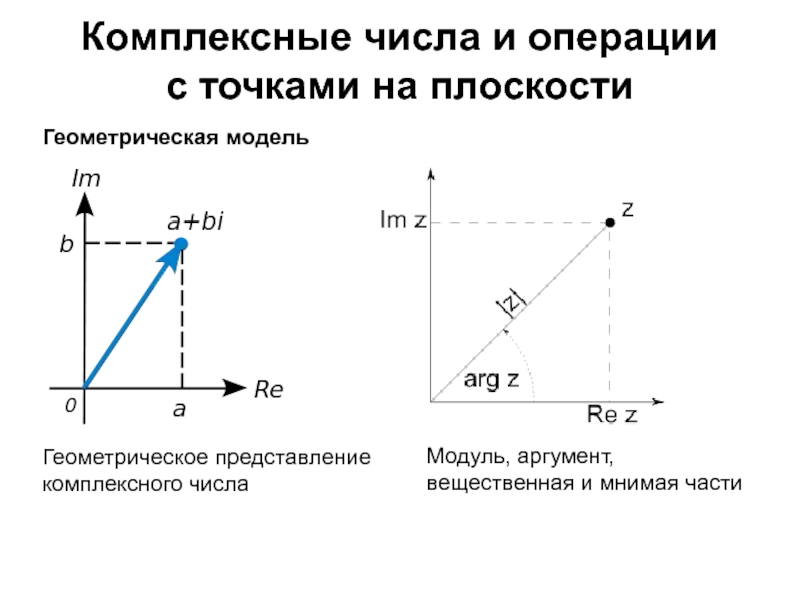
Слайд 29Комплексные числа и операции
с точками на плоскости
Геометрическая модель
Геометрическое представление
комплексного
числа
Модуль, аргумент, вещественная и мнимая части
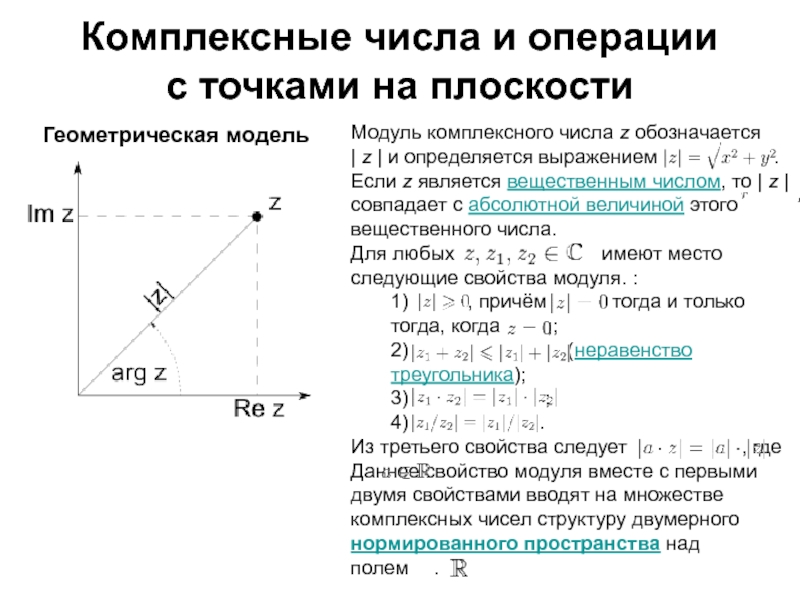
Слайд 30Комплексные числа и операции
с точками на плоскости
Геометрическая модель
Модуль комплексного
числа z обозначается
| z | и определяется выражением .
Если z является вещественным числом, то | z | совпадает с абсолютной величиной этого вещественного числа.Для любых имеют место следующие свойства модуля. :
1) , причём тогда и только тогда, когда ;;
2) (неравенство треугольника);
3) ;
4) .
Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .
Слайд 31Кватернионы и операции
с точками пространства
Кватернион представляет собой паруКватернион представляет
собой пару где — вектор трёхмерного пространства,
а — скаляр, то есть вещественное число. Операции сложения определены следующим образом:Произведение определяется следующим образом:
где * обозначает скалярное произведение,
а — векторное произведение.
Слайд 32Кватернионы и операции
с точками пространства
Кватернионы можно определить как формальную
сумму где — вещественные числа, а
— мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов — — выглядит так:например, , a .
Так же, как и для комплексных чисел,
называется модулем .
Кватернионы и повороты пространства
Организация трёх степеней свободы, но окончательная свобода меньших колец зависит от положения больших колец
Слайд 33Октонионы и операции
с точками пространства
Октонион (октава, число Кэли) — это
линейная комбинация элементов .
Каждая октава x может быть
записана в формес вещественными коэффициентами . Норма октониона
Таблица умножения
элементов октавы:
Слайд 35
произведение сумм четырёх квадратов является суммой четырёх квадратов.
Других чисел нет!
Тождество
Эйлера о четырёх квадратах — математическая теорема о том, что
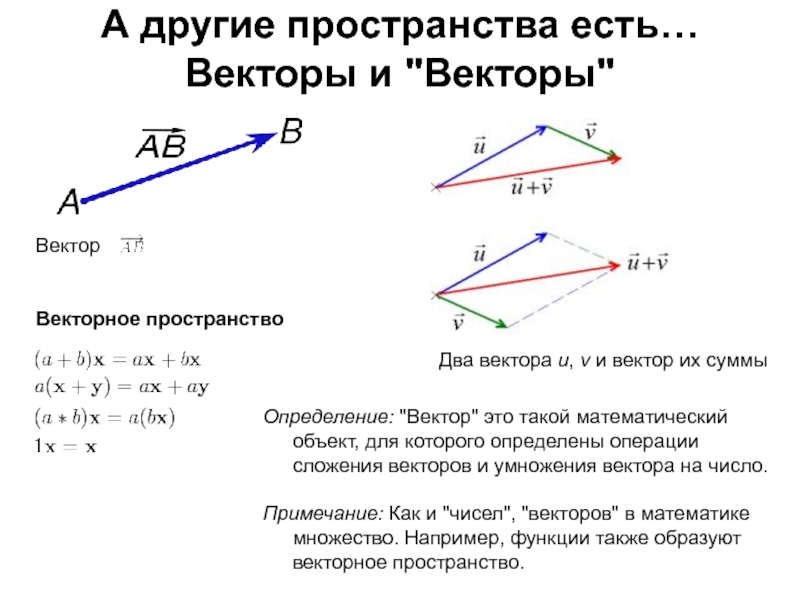
Слайд 37А другие пространства есть…
Векторы и "Векторы"
Вектор
Векторное пространство
Два
вектора u, v и вектор их суммы
Определение: "Вектор" это такой
математический объект, для которого определены операции сложения векторов и умножения вектора на число.Примечание: Как и "чисел", "векторов" в математике множество. Например, функции также образуют векторное пространство.
Слайд 38А другие пространства есть…
Матрицы
Матрица — математический объект, записываемый в виде прямоугольной
таблицы чисел, которая представляет собой совокупность строк — математический объект, записываемый
в виде прямоугольной таблицы чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.Сложение матриц A + B есть операция нахождения матрицы C,
Умножение матриц (обозначение: AB) — вычисление матрицы C,
Слайд 39Задачи и матрицы.
Системы линейных уравнений
Систему из m уравнений с n
неизвестными
можно представить в матричном виде
и тогда всю систему
можно записать так:AX = B.
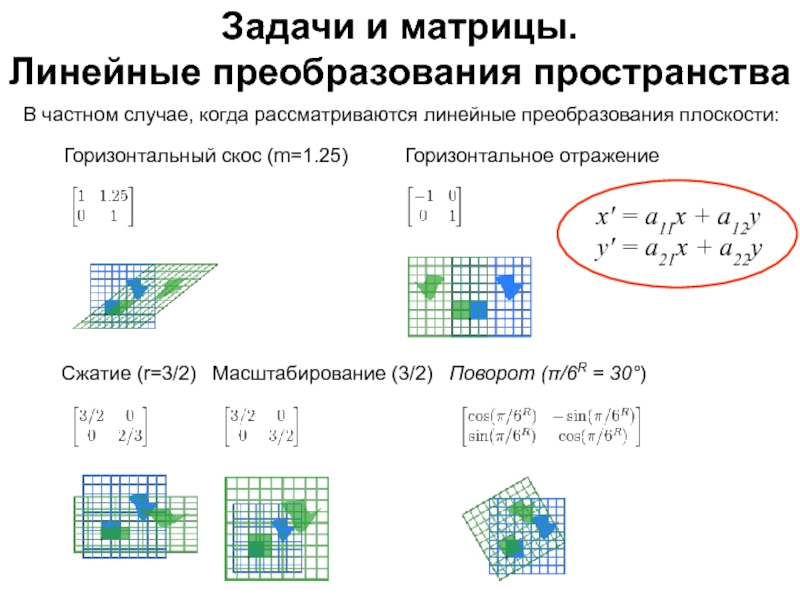
Слайд 40В частном случае, когда рассматриваются линейные преобразования плоскости:
x' = a11x + a12y
y' = a21x + a22y
Задачи и матрицы.
Линейные преобразования пространства
Слайд 41Представление чисел в компьютерных системах
Подробнее см.
Целочисленные Целочисленные: со
знаком, то есть могут принимать как положительные, так и отрицательные
значения; и без знака, то есть могут принимать только неотрицательные значения.Вещественные Вещественные: с запятой Вещественные: с запятой (то есть хранятся знак и цифры целой и дробной частей) и с плавающей запятой (то есть число приводится к виду m*be, где m — мантисса, где m — мантисса, b — основание показательной функции, где m — мантисса, b — основание показательной функции, e — показатель степени (порядок, где m — мантисса, b — основание показательной функции, e — показатель степени (порядок) (в англоязычной литературе экспонента), причём в нормальной форме 0<=m
Слайд 42Представление чисел и других данных в компьютерных системах
Подробнее см.
Контрольный
вопрос по предыдущей лекции. Действительно ли каждый бит натурального числа,
записанного в компьютере в двоичной системе, имеет информативность 1 бит?Подсказка: Все дело в разрядности и диапазоне значений.
Слайд 43Натуральные двоичные числа
Преобразование десятичных чисел в двоичные
19 /2 =
9 с остатком 1
9 /2 = 4 c остатком
14 /2 = 2 без остатка 0
2 /2 = 1 без остатка 0
1 /2 = 0 с остатком 1
В результате получаем число 19 в двоичной записи: 10011.
Преобразование двоичных чисел в десятичные
Пусть дано двоичное число 110001. Для перевода в десятичное запишите его справа налево как сумму по разрядам следующим образом:
.
Слайд 44Информативность натуральных двоичных чисел
Вопрос: Число больше порога? Да –
1, Нет – 0.
0
255
0
0
1
0
0
1
0 0 1 0 0 1…
число
Числовой диапазон
порог
каждый раз делитоставшийся диапазон пополам,
поэтому априорная вероятность ответов ½,
и апостериорная информативность их – 1 бит.
Слайд 45Представление целых чисел в ЭВМ
Дополнительный код (англ. two’s complement, иногда
twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в
компьютерах) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение). Либо вычитанием числа из нуля.Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. .
Слайд 46Представление дробных чисел в ЭВМ
Число с фиксированной запятой — формат
представления рационального или вещественного числа в памяти ЭВМ — формат представления
рационального или вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление x′ связаны формулой ,где z — цена (вес) младшего разряда.
Простейший пример арифметики с фиксированной запятой — перевод рублейПростейший пример арифметики с фиксированной запятой — перевод рублей в копейки. В таком случае, чтобы запомнить сумму 12 рублей 34 копейки, мы записываем в ячейку памяти число 1234.
Недостаток фиксированной запятой — очень узкий диапазон чисел, с угрозой переполненияНедостаток фиксированной запятой — очень узкий диапазон чисел, с угрозой переполнения на одном конце диапазона и потерей точностиНедостаток фиксированной запятой — очень узкий диапазон чисел, с угрозой переполнения на одном конце диапазона и потерей точности вычислений на другом. Эта проблема и привела к изобретению плавающей запятойНедостаток фиксированной запятой — очень узкий диапазон чисел, с угрозой переполнения на одном конце диапазона и потерей точности вычислений на другом. Эта проблема и привела к изобретению плавающей запятой. Например: если нужна точность в 3 значащих цифры, 4-байтовая фиксированная запятая даёт диапазон в 6 порядков (то есть, разница приблизительно 106 между самым большим и самым маленьким числом), 4-байтовое число одинарной точности — в 70 порядков.
Слайд 47Представление действительных чисел
Плавающая запятая — форма представления действительных чисел, в
которой число хранится в форме мантиссы — форма представления действительных чисел,
в которой число хранится в форме мантиссы и показателя степени — форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Например, число 1,528535047×10−25 в большинстве языков программирования высокого уровня записывается как 1.528535047E-25.
S — знак, E — показатель степени, I — целая часть, F — дробная часть
Так же, как и для целых, знаковый бит — старший.
Слайд 48Типы данных
Подробнее см.
Простые.
Перечислимый тип. Может хранить только те
значения, которые прямо указаны в его описании.
Числовые данные.
Символьный типСимвольный
тип. Хранит один символСимвольный тип. Хранит один символ. Могут использоваться различные кодировки.Логический типЛогический тип. Имеет два значения: истинаЛогический тип. Имеет два значения: истина и ложьЛогический тип. Имеет два значения: истина и ложь, при троичной логикеЛогический тип. Имеет два значения: истина и ложь, при троичной логике может иметь и третье значение — «не определено» (или «неизвестно»). Могут применяться логические операцииЛогический тип. Имеет два значения: истина и ложь, при троичной логике может иметь и третье значение — «не определено» (или «неизвестно»). Могут применяться логические операции. Используется в операторах ветвленияЛогический тип. Имеет два значения: истина и ложь, при троичной логике может иметь и третье значение — «не определено» (или «неизвестно»). Могут применяться логические операции. Используется в операторах ветвления и циклахЛогический тип. Имеет два значения: истина и ложь, при троичной логике может иметь и третье значение — «не определено» (или «неизвестно»). Могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипомЛогический тип. Имеет два значения: истина и ложь, при троичной логике может иметь и третье значение — «не определено» (или «неизвестно»). Могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипом числового типа, при этом ложь=0, истина=1.
МножествоМножество. В основном совпадает с обычным математическимМножество. В основном совпадает с обычным математическим понятием множестваМножество. В основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип.
Слайд 49Типы данных
Подробнее см.
Составные (сложные).
МассивМассив. Является индексированным набором элементов
одного типа. Одномерный массивМассив. Является индексированным набором элементов одного типа.
Одномерный массив — векторМассив. Является индексированным набором элементов одного типа. Одномерный массив — вектор, двумерный массивМассив. Является индексированным набором элементов одного типа. Одномерный массив — вектор, двумерный массив — матрица.Строковый типСтроковый тип. Хранит строкуСтроковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенацияСтроковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенация (прибавление одной строки в конец другой строки). В языках, близких к бинарному представлению данных, чаще рассматривается как массив символов, в языках более высокой абстракции зачастую выделяется в качестве простого.
Запись (структура). Набор различных элементов (полей записи), хранимый как единое целое. Возможен доступ к отдельным полям записи. Например, struct в C или record в Pascal.
Класс.
Файловый типФайловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файлФайловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включённый в некоторые системы программированияФайловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включённый в некоторые системы программирования, фактически является неявным массивом).
УказательУказатель. Хранит адресУказатель. Хранит адрес в памяти компьютераУказатель. Хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — указательУказатель. Хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — указатель на переменную.
Ссылка.
Слайд 50Типы данных
Подробнее см.
Структурные типы данных
Регулярные массивы
Структуры (записи, кортежи)
Динамические
списки и массивы переменной длинны
Ациклические графы (деревья)
Сетевые графы
Специализированные типы данных
Таблицы
и базы данныхТекст (символы и символьные строки)
Аудиоданные
Векторная и растровая графика
Слайд 51Типы данных. Массив
Индексный массив — именованный набор однотипных переменных,
расположенных в памяти непосредственно друг за другом, доступ к которым
осуществляется по индексу, расположенных в памяти непосредственно друг за другом, доступ к которым осуществляется по индексу (в отличие от списка).Индекс массива — целое число, либо значение типа, приводимого к целому, указывающее на конкретный элемент массива.
Примеры:
int Array[10]; // Одномерный массив целых чисел размера 10
// Нумерация элементов от 0 до 9
double Array[12][15]; // Двумерный массив вещественных чисел двойной точности
// размера 12 на 15. Нумерация строк от 0 то 11, столбцов от 0 до 14
Достоинства массива как структуры данных
лёгкость вычисления адреса элемента по его индексу (поскольку элементы массива располагаются один за другим)
одинаковое время доступа ко всем элементам
экономия памяти - элементы состоят только из информационного поля
Недостатки
невозможность удаления или добавления элемента без сдвига других
при работе с массивом в стиле C (с указателями*) и при отсутствии дополнительных средств контроля — угроза выхода за границы массива и повреждения данных
*Указатель Хранит адрес Хранит адрес в памяти компьютера Хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — указатель Хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — указатель на переменную.
Слайд 52Типы данных. Структура
Структура — конструкция большинства языков программирования, позволяющая содержать
в себе фиксированный набор переменных различных типов.
В языках семейства Pascal
структуры традиционно называют записями (англ. record). Пример объявления структуры на C:
struct str_name {
int member_1;
float member_2;
char member_3[256];
};
Пример объявления структуры на Pascal:
type str_name = record
begin
member_1 : integer;
member_2 : extended;
member_3 : string;
end;
Слайд 53Типы данных. Список
Связный список — структура данных, состоящая из узлов —
структура данных, состоящая из узлов, каждый из которых содержит как
собственно данные — структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.Достоинства списка как структуры данных
лёгкость добавления и удаления элементов
размер ограничен только объёмом памяти и разрядностью указателей
Недостатки
сложность определения адреса элемента по его индексу (номеру) в списке
на поля-указатели (указатели на следующий и предыдущий элемент) расходуется дополнительная память
работа со списком медленнее, чем с массивами, так как к любому элементу списка можно обратиться, только пройдя все предшествующие ему элементы
элементы списка могут быть расположены в памяти разреженно, что окажет негативный эффект на кэширование процессора
над связными списками гораздо труднее (хотя и в принципе возможно) производить параллельные векторные операции, такие как вычисление суммы
Односвязный список Кольцевой связный список
Двусвязный список
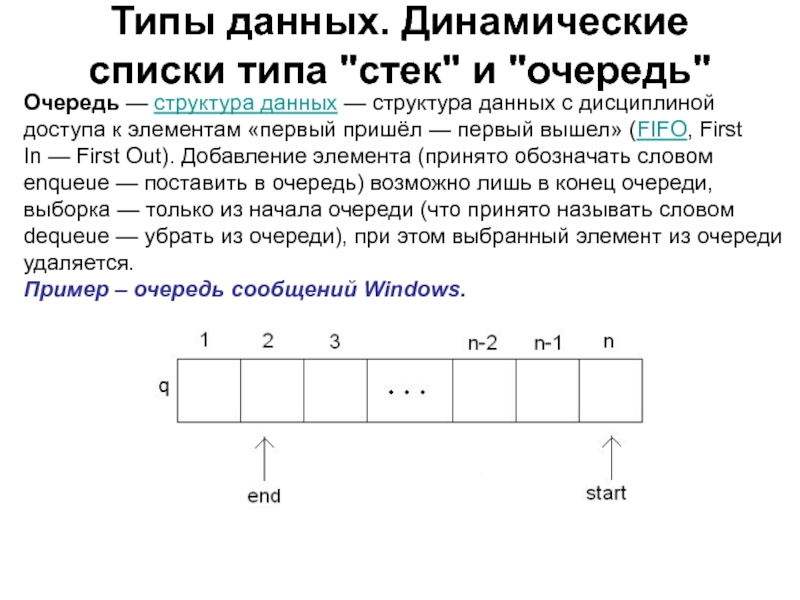
Слайд 54Типы данных. Динамические списки типа "стек" и "очередь"
Очередь — структура
данных — структура данных с дисциплиной доступа к элементам «первый пришёл —
первый вышел» (FIFO, First In — First Out). Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется.Пример – очередь сообщений Windows.
Слайд 55Типы данных. Динамические списки типа "стек" и "очередь"
Стек (англ. stack —
стопка) — структура данных, в которой доступ к элементам организован по
принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»). Чаще всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую сверху, нужно снять верхнюю.Добавление элемента, называемое также проталкиванием (push), возможно только в вершину стека (добавленный элемент становится первым сверху). Удаление элемента, называемое также выталкиванием (pop), тоже возможно только из вершины стека, при этом второй сверху элемент становится верхним. Пример – стек вызова подпрограмм (рекурсивый вызов функций).
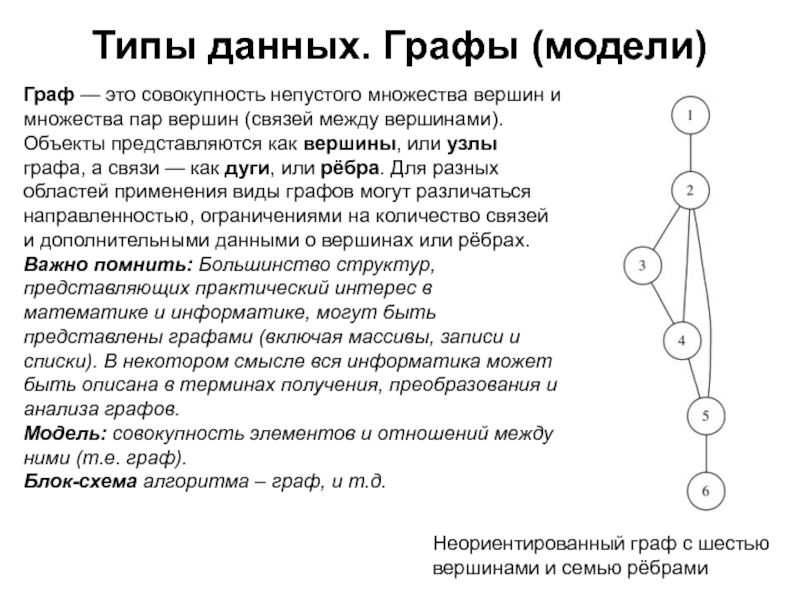
Слайд 56Типы данных. Графы (модели)
Граф — это совокупность непустого множества вершин
и множества пар вершин (связей между вершинами).
Объекты представляются как вершины,
или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.Важно помнить: Большинство структур, представляющих практический интерес в математике и информатике, могут быть представлены графами (включая массивы, записи и списки). В некотором смысле вся информатика может быть описана в терминах получения, преобразования и анализа графов.
Модель: совокупность элементов и отношений между ними (т.е. граф).
Блок-схема алгоритма – граф, и т.д.
Неориентированный граф с шестью вершинами и семью рёбрами
Слайд 57Типы данных. Графы (модели)
Неориентированный граф G — это упорядоченная пара
G: = (V,E), для которой выполнены следующие условия: V —
это непустое множество вершин, или узлов, E — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Вершины u и v называются концевыми вершинами (или просто концами) ребра e = {u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают, то есть e = {v,v}. Степенью deg V вершины V называют количество инцидентных ей рёбер(при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
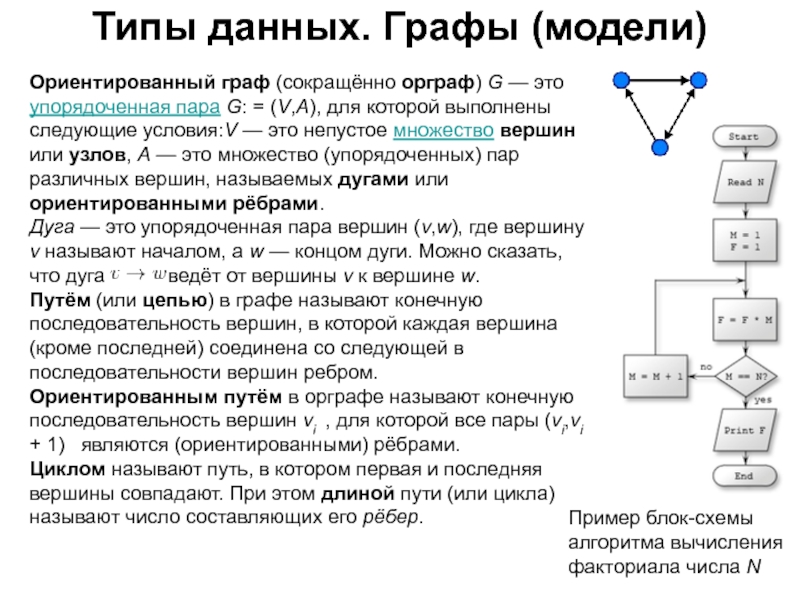
Слайд 58Типы данных. Графы (модели)
Ориентированный граф (сокращённо орграф) G — это
упорядоченная пара G: = (V,A), для которой выполнены следующие условия:V
— это непустое множество вершин или узлов, A — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.Дуга — это упорядоченная пара вершин (v,w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга ведёт от вершины v к вершине w.
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi , для которой все пары (vi,vi + 1) являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.
Пример блок-схемы алгоритма вычисления факториала числа N
Слайд 59Типы данных. Графы (модели)
Граф называется:
связным, если для любых вершин
u,v есть путь из u в v.
сильно связным или
ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь. деревом, если он связный и не содержит простых циклов.
полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.
двудольным, если его вершины можно разбить на два непересекающихся подмножества V1 и V2 так, что всякое ребро соединяет вершину из V1 с вершиной из V2.
k-дольным, если его вершины можно разбить на k непересекающихся подмножества V1, V2, …, Vk так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.
взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.
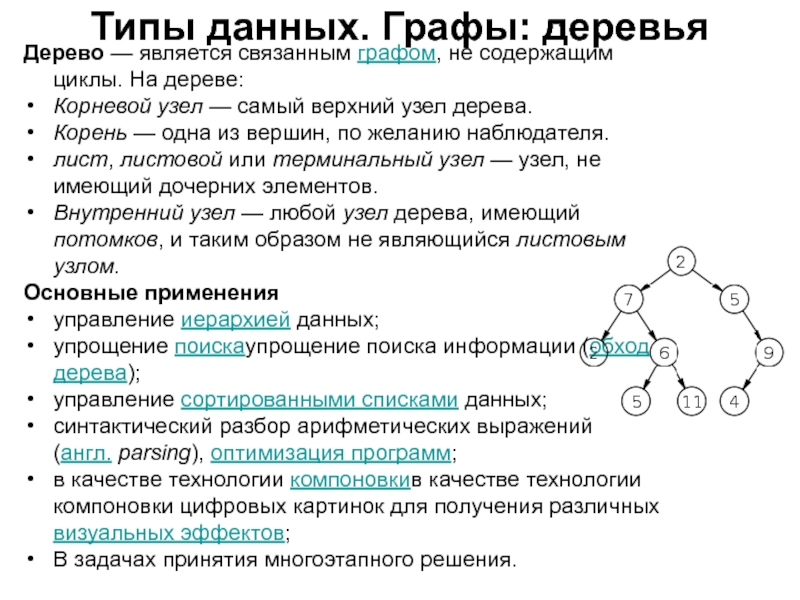
Слайд 60Типы данных. Графы: деревья
Дерево — является связанным графом, не содержащим
циклы. На дереве:
Корневой узел — самый верхний узел дерева.
Корень — одна
из вершин, по желанию наблюдателя.лист, листовой или терминальный узел — узел, не имеющий дочерних элементов.
Внутренний узел — любой узел дерева, имеющий потомков, и таким образом не являющийся листовым узлом.
Основные применения
управление иерархией данных;
упрощение поискаупрощение поиска информации (обход дерева);
управление сортированными списками данных;
синтактический разбор арифметических выражений (англ. parsing), оптимизация программ;
в качестве технологии компоновкив качестве технологии компоновки цифровых картинок для получения различных визуальных эффектов;
В задачах принятия многоэтапного решения.
Слайд 62Типы данных. Таблицы. Базы данных
Подробнее см.
Кортежи. Таблицы. Реляционные базы
данных. SQL.
Копейкин М.В., Спиридонов В.В., Шумова Е.O. Базы данных. Основы
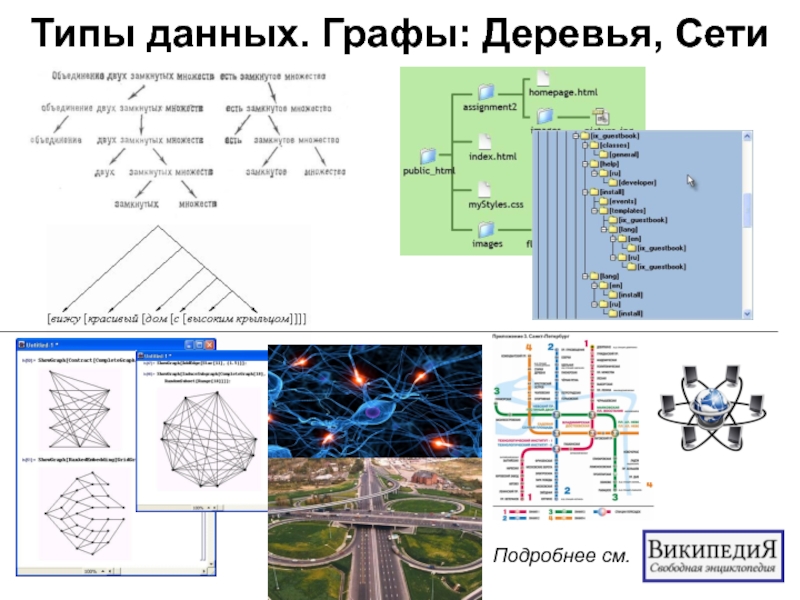
SQL реляционных баз данных: Учебное пособие. - СПб.: СЗТУ, 2005. - 160 с. Слайд 63Типы данных. Кодирование данных
Подробнее см.
Структурные типы данных
Регулярные массивы
Динамические
списки и массивы переменной длинны
Ациклические графы (деревья)
Сетевые графы
Специализированные типы данных
Таблицы
и базы данныхТекст (символы и символьные строки)
Аудиоданные
Векторная и растровая графика
Кодирование данных - преобразования, касающиеся не содержания, а формы представления данных:
Сжатие (хранение и передача данных)
Помехоустойчивое кодирование (передача данных)
Криптография (защита данных)
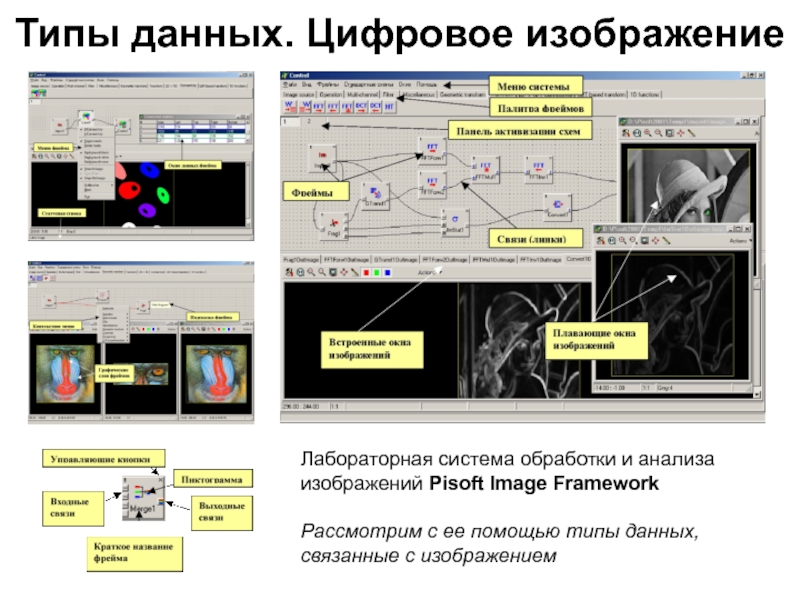
Слайд 64Типы данных. Цифровое изображение
Лабораторная система обработки и анализа изображений
Pisoft Image Framework
Рассмотрим с ее помощью типы данных, связанные с
изображением Слайд 65Компьютерное зрение как типовая область компьютерной обработки информации
Специализированное
зрение без "встроенных" алгоритмов.
Требования к системам и алгоритмам технического
зрения: надежность, точность, быстродействие.Основные задачи анализа изображений.
Компьютерное зрение = "геометрия сегодня"
Слайд 67Компьютерное зрение
как школьная геометрия++
Отличия КЗ от классической геометрии:
1. Увеличение
числа точек на порядки.
2. Появление у точек атрибутов интенсивности, цвета
и других характеристик.3. Рассмотрение не только правильных фигур, но и фигур любых других форм.
4. Учет всякого рода неидеальностей, погрешностей, шумов, искажений, дискретностей, неполной наблюдаемости и т.п. реальных факторов, которые, впрочем, также имеют математическое выражение.