Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное дифференцирование
Содержание
- 1. Численное дифференцирование
- 2. При вычислении производной функции, будем иметь в
- 3. Таким образом, вычисляется производная в середине промежутка.
- 4. Для производной третьего порядка можно использовать следующую
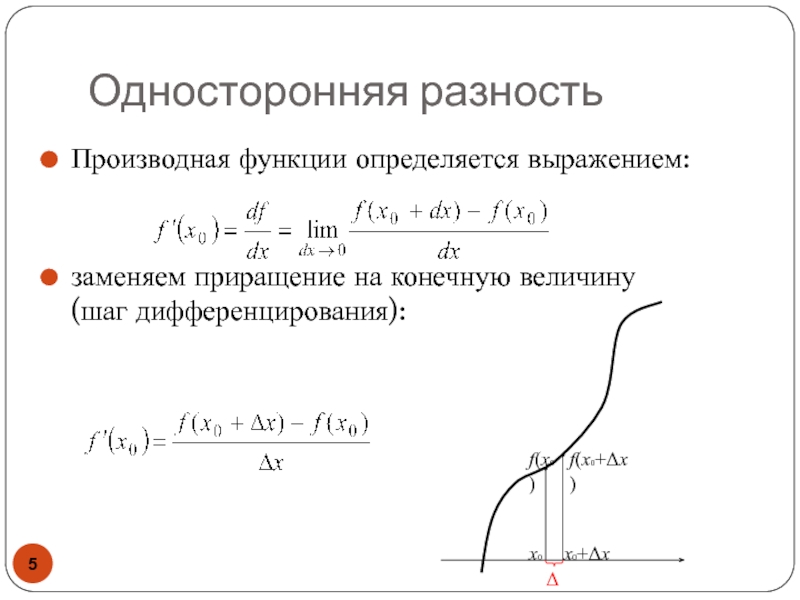
- 5. Односторонняя разностьПроизводная функции определяется выражением: заменяем приращение на конечную величину (шаг дифференцирования):x0f(x0)f(x0+Δx)x0+ΔxΔx
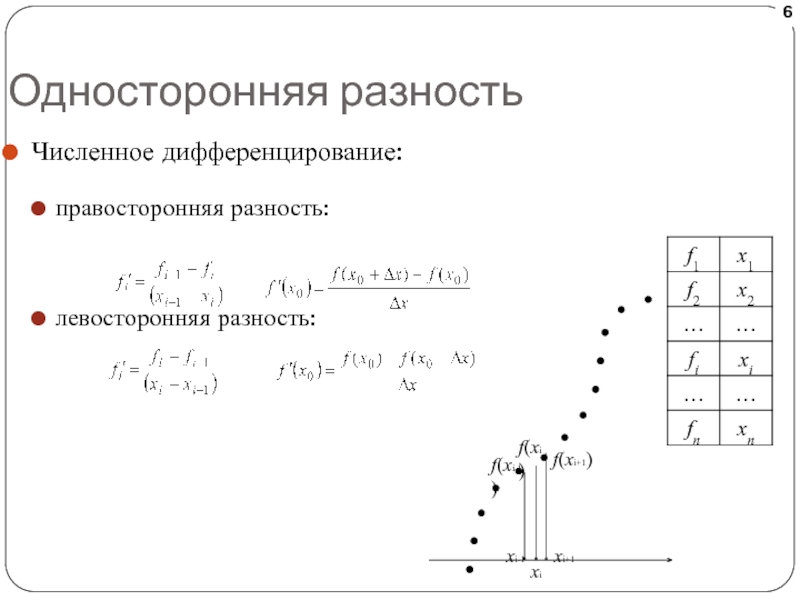
- 6. Односторонняя разностьЧисленное дифференцирование:правосторонняя разность:левосторонняя разность:xif(xi)f(xi+1)xi-1 xi+1f(xi-1)
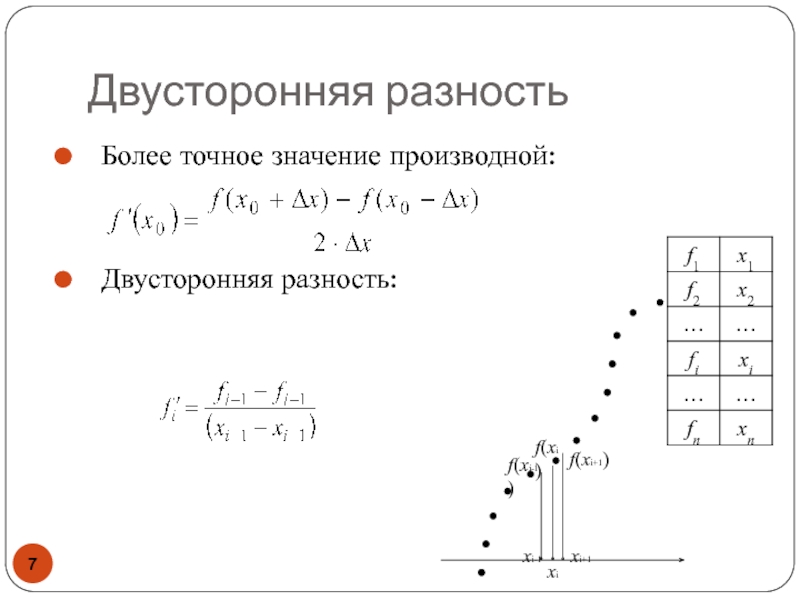
- 7. Двусторонняя разностьБолее точное значение производной:Двусторонняя разность:xif(xi)f(xi+1)xi-1 xi+1f(xi-1)
- 8. Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона
- 9. Оценка погрешности и точности вычисления не менее
- 10. Слайд 10
- 11. Мы будем пользоваться формулой (2), а впоследствии
- 12. Частное дифференцирование функции от многих переменныхВсе аргументы
- 13. Интерполяция полиномом Заданная таблица сглаживается какой-либо функцией
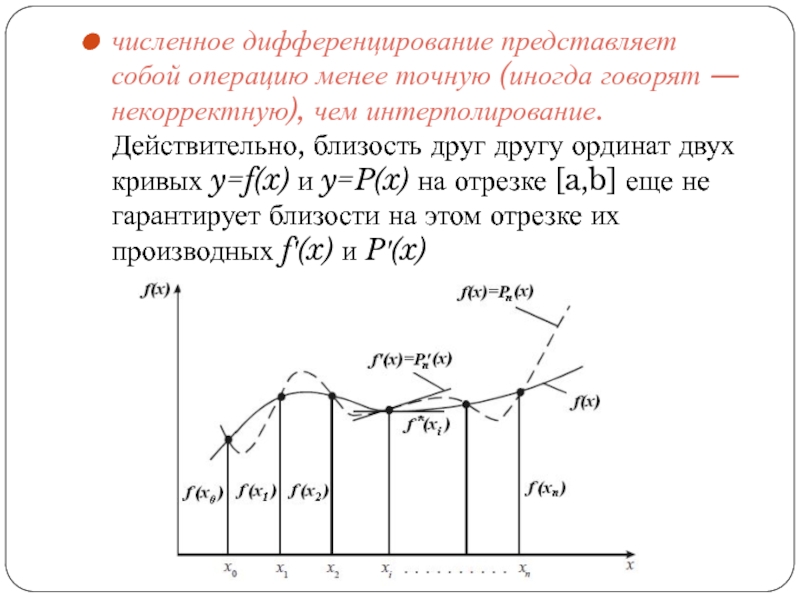
- 14. численное дифференцирование представляет собой операцию менее точную
- 15. Интерполяция конечными разностямиВ этом случае (x*= xi
- 16. Выразим yi’, разделив предварительно на h и оставляя слагаемые с первой степенью шага h, получим
- 17. где — центральная разность первого порядка
- 18. Метод Рунге С целью оценки погрешности продифференцируем
- 19. Из этого выражения видно, что это уже метод порядка p+1, т.е. на порядок точнее
- 20. Скачать презентанцию
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева на равном расстоянии от - точке, в которой
Слайды и текст этой презентации
Слайд 1К численному (приближенному) дифференцированию чаще всего прибегают, когда приходится вычислять
производные от функций, заданных таблично, или, когда непосредственное дифференцирование затруднительно.
дифференцирование
Слайд 2При вычислении производной функции, будем иметь в виду, что один
из способов найти производную
- это взять достаточно малые значения справа
и слева на равном расстоянии от - точке, в которой мы хотим найти производную.
Слайд 3Таким образом, вычисляется производная в середине промежутка. По значениям f'
можно таким же способом найти производную от f', т.е. f''.
Можно выразить f'' непосредственно через f(x):
Слайд 4Для производной третьего порядка можно использовать следующую формулу:
Возникают естественные
вопросы, откуда происходят эти формулы и как оценивать точность вычисления
производных по этим формулам?
Слайд 5Односторонняя разность
Производная функции определяется выражением:
заменяем приращение на конечную величину
(шаг дифференцирования):
x0
f(x0)
f(x0+Δx)
x0+Δx
Δx
Слайд 6Односторонняя разность
Численное дифференцирование:
правосторонняя разность:
левосторонняя разность:
xi
f(xi)
f(xi+1)
xi-1
xi+1
f(xi-1)
Слайд 7Двусторонняя разность
Более точное значение производной:
Двусторонняя разность:
xi
f(xi)
f(xi+1)
xi-1
xi+1
f(xi-1)
Слайд 8Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона и других. Сущность
которых состоит в том, что заданная функция f(x) представляется в
виде многочлена, который значительно проще дифференцировать, чем какие-либо другие функции, особенно трансцендентные или представляющие собой сложные выражения.
Слайд 9Оценка погрешности и точности вычисления не менее серьезный и сложный
процесс, чем само приближенное вычисление. Так для оценки погрешности дифференцирования
могут быть применены следующие формулы:где предполагается, что функция f(x) дифференцируемая
n + 1 раз, а точка
- некоторое промежуточное значение между x0 - точкой, в которой находится производная и точками (x0 - 2dx), (x0 - dx), (x0 + dx), (x0 + 2dx), ...
из заданного промежутка [a, b].
(2)
Слайд 10 На практике f (n+1)(c) оценивать непросто, поэтому при малых dx
приближенно полагают:
и тогда получается следующая формула
(3)
Слайд 11Мы будем пользоваться формулой (2), а впоследствии и формулой (3),
в зависимости от конкретной задачи и тех сложностей, которые могут
возникнуть при составлении программ. Используя эти формулы, составим функцию для вычисления первой производной. Точность вычисления eps задается пользователем, а первоначальная величина промежутка dx устанавливается 1, а затем, для уточнения вычисления - делится на 2.
Слайд 12Частное дифференцирование функции от многих переменных
Все аргументы функции становятся константами,
кроме аргумента по которому проводится дифференцирование
Требуемый порядок производной получается путем
последовательного вычисления производных, вплоть до требуемого порядка
Слайд 13Интерполяция полиномом
Заданная таблица сглаживается какой-либо функцией P(x), являющейся интерполяционным полиномом,
или полиномом, полученным с использованием МНК (метода наименьших квадратов) с
некоторой погрешностью Rn(x), в результате чего имеют место следующие равенства:f(x) = P(x) + Rn(x), f(x*) = P(x*) + Rn(x*):
f′(x) = P′(x) + R′n(x), f′(x*) = P′(x*) + R′n(x*):
f′′(x) = P′′(x) + R′′n(x), f′′(x*) = P′′(x*) + R′′n(x*)
Слайд 14численное дифференцирование представляет собой операцию менее точную (иногда говорят —
некорректную), чем интерполирование. Действительно, близость друг другу ординат двух кривых
y=f(x) и y=P(x) на отрезке [a,b] еще не гарантирует близости на этом отрезке их производных f′(x) и P′(x)
Слайд 15Интерполяция конечными разностями
В этом случае (x*= xi , i =
0,…, n) используется аппарат разложения функций в ряд Тейлора, для
чего функция в точке x* должна иметь достаточное число производных. Предполагается, что заданная таблица является сеточной функцией для некоторой функции y(x) (т.е. yi = y(xi )), имеющей в точке производные до четвертого порядка включительно. (9.3)
Слайд 16Выразим yi’, разделив предварительно на h и оставляя слагаемые с
первой степенью шага h, получим
Слайд 18Метод Рунге
С целью оценки погрешности продифференцируем численно методом p-го
порядка функцию f(xi) = yi , i = 0,…, n с шагом h. Затем продифференцируем численно функцию
тем же методом p-го порядка, с шагом kh (k=1/2; 1/4; 1/16; ...)
