Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Деревья. Алгоритм Краскала
Содержание
- 1. Деревья. Алгоритм Краскала
- 2. ПОВТОРЕНИЕГраф называется связным, если для любых двух
- 3. ОПРЕДЕЛЕНИЕ ДЕРЕВАДеревом называется связный граф с выделенной
- 4. СВОЙСТВА ДЕРЕВЬЕВВ дереве любые две вершины связаны
- 5. СВО ЙСТВА ДЕРЕВЬЕВГраф G(V, X ) является деревом
- 6. Дерево с n вершинами имеет n –1 ребро, поэтому оно будет минимальным связным графом.
- 7. Лес – это граф, компоненты которого
- 8. Бинарное дерево называется деревом поиска, если его
- 9. Пирамида - это такое двоичное дерево, для
- 10. СЕТИ. СЕТЕВЫЕ МОДЕЛИ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ Граф называется
- 11. АЛГОРИТМ КРАСКАЛА Имеется n сельских домов, которые
- 12. ПОСТАНОВКА ЗАДАЧИДан связный неориентированный граф G(V;E), и
- 13. ОПИСАНИЕ АЛГОРИТМА1. Вначале текущее множество рѐбер устанавливается
- 14. началовыбор первого ребра с минимальным весомвыбор следующего
- 15. ПРИМЕРРебра AD и CE имеют минимальный вес,
- 16. ПРИМЕРАналогично выбираем ребро DF, вес которого равен
- 17. ПРИМЕРАналогичным образом выбирается ребро BE, вес которого
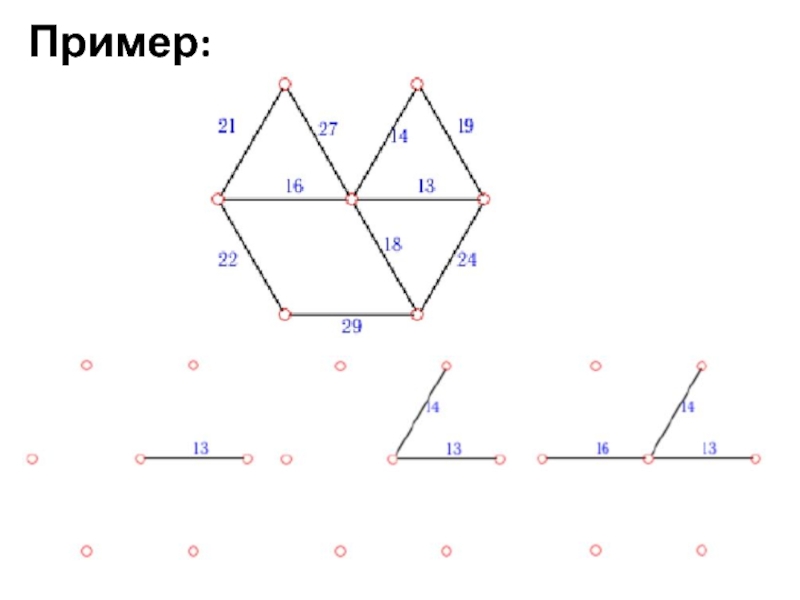
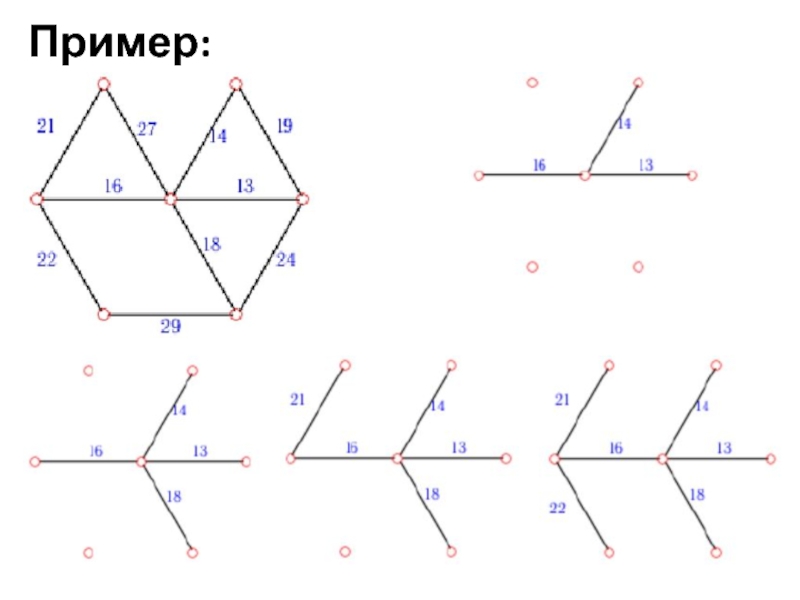
- 18. Пример:
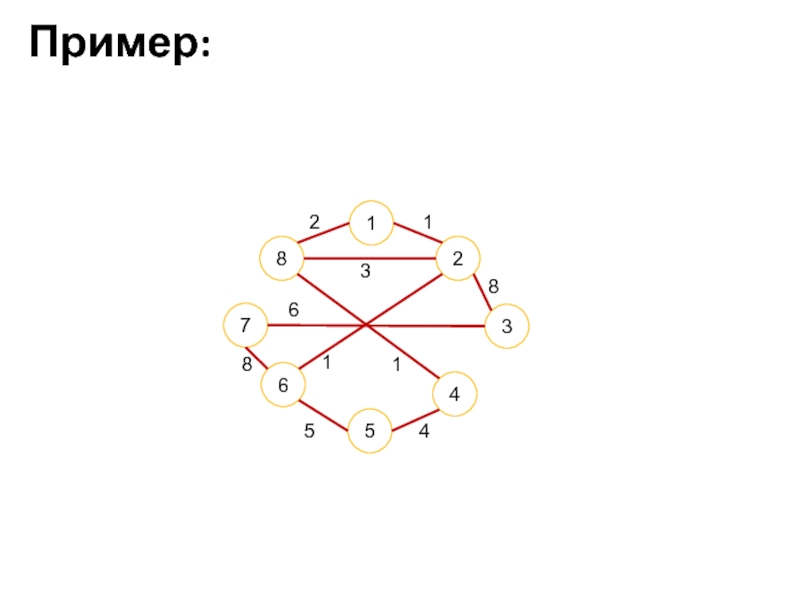
- 19. Пример:
- 20. 178264351328611458Пример:
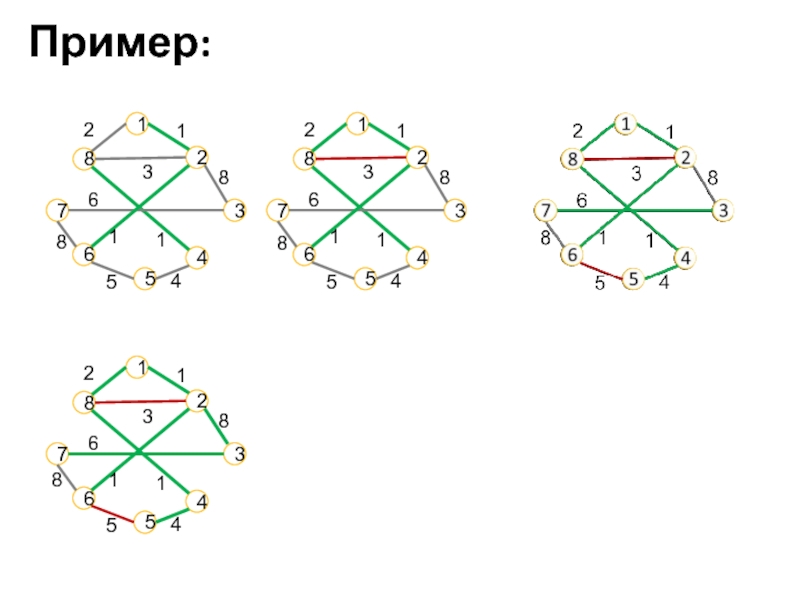
- 21. 178264351328611458178264351328611458178264351328611458Пример:
- 22. Пример:
- 23. Контрольные вопросы:1. Что называется деревом в графе?
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Деревья. Алгоритм Краскала
1. Деревья и их свойства.
2. Алгоритм Краскала нахождения
минимального остовного дерева
Слайд 2ПОВТОРЕНИЕ
Граф называется связным, если для любых двух его вершин имеется
путь, соединяющий эти вершины.
Граф – это множество точек, называемых вершинами,
и множество линий, называемых ребрами, которые соединяют пары вершин (или вершину саму с собой).Длиной маршрута называется количество ребер в нем. Расстоянием между вершинами u, v (обозначается s(u,v)) называется наименьшая длина цепи < u,v >
Маршрутом в графе называется последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной
Маршрут, в котором все ребра различны, называется цепью (путем)
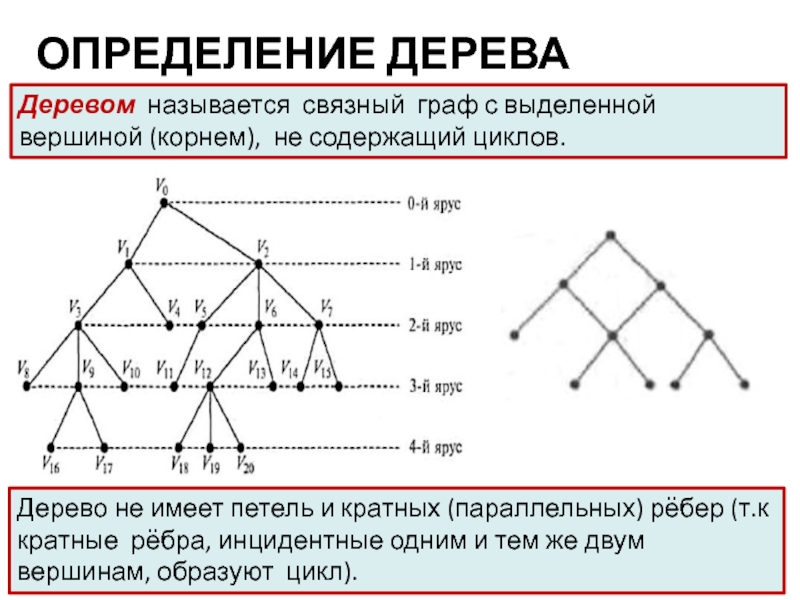
Слайд 3ОПРЕДЕЛЕНИЕ ДЕРЕВА
Деревом называется связный граф с выделенной вершиной (корнем), не
содержащий циклов.
Дерево не имеет петель и кратных (параллельных) рёбер
(т.к кратные рёбра, инцидентные одним и тем же двум вершинам, образуют цикл). Слайд 4СВОЙСТВА ДЕРЕВЬЕВ
В дереве любые две вершины связаны единственной цепью
Любая ветвь
дерева является мостом – при ее удалении граф распадается на
две части (два подграфа)Для каждой пары вершин дерева (узлов) существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины.
Расстояние до корневой вершины V0 называется ярусом s вершины, s = d(V0,V).
Узел без поддеревьев называется листом и является висячей вершиной.
Слайд 5СВО ЙСТВА ДЕРЕВЬЕВ
Граф G(V, X ) является деревом тогда и только
тогда, когда выполняется хотя бы одно из условий:
граф G(V,X
) связан и не содержит циклов; граф G(V, X ) не содержит циклов и имеет n –1 ребро;
граф G(V, X ) связан и имеет n –1 ребро;
граф G(V, X ) не содержит циклов, но добавление ребра между несмежными вершинами приводит к появлению одного и только одного элементарного цикла;
граф G(V, X ) связный, но утрачивает это свойство после удаления любого ребра;
в графе G(V, X ) всякая пара вершин соединена цепью, и притом только одной.
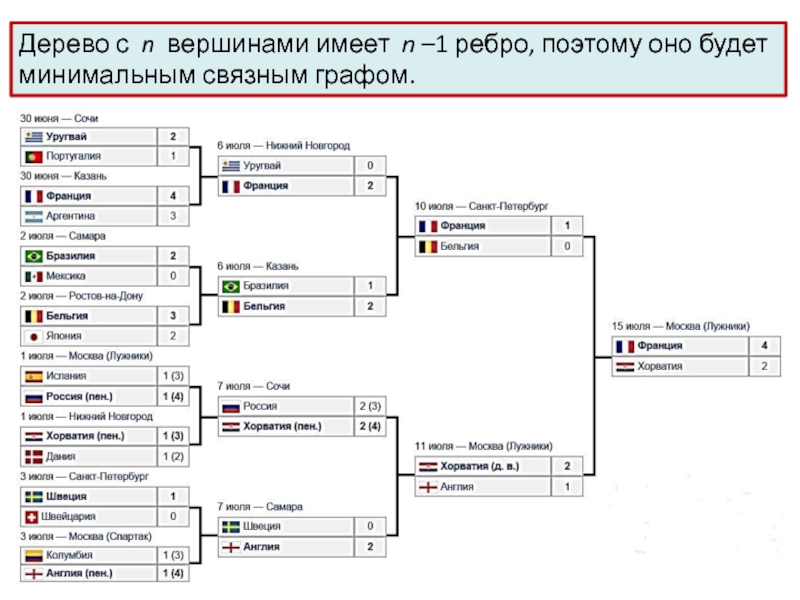
Дерево с n вершинами имеет n –1 ребро, поэтому оно будет минимальным связным графом.
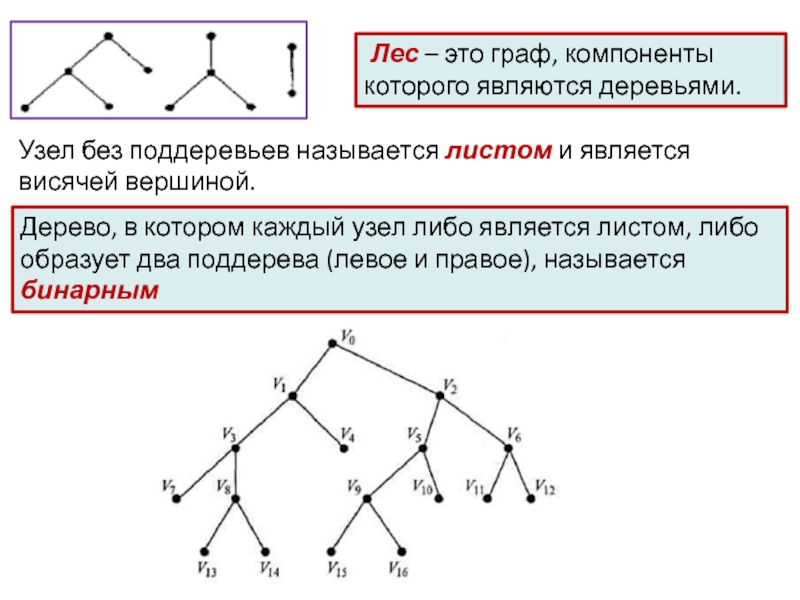
Слайд 7 Лес – это граф, компоненты которого являются деревьями.
Узел без
поддеревьев называется листом и является висячей вершиной.
Дерево, в котором
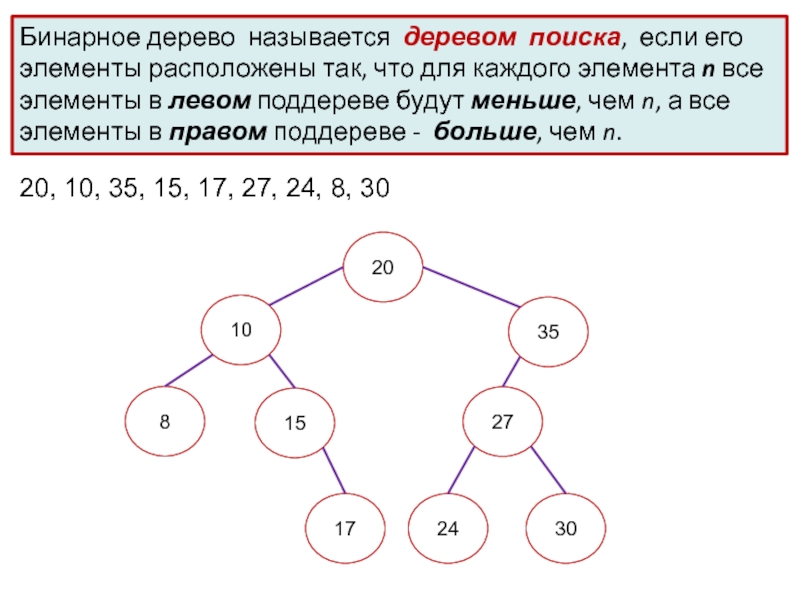
каждый узел либо является листом, либо образует два поддерева (левое и правое), называется бинарнымСлайд 8Бинарное дерево называется деревом поиска, если его элементы расположены так,
что для каждого элемента n все элементы в левом поддереве
будут меньше, чем n, а все элементы в правом поддереве - больше, чем n.20, 10, 35, 15, 17, 27, 24, 8, 30
20
10
35
8
15
27
30
24
17
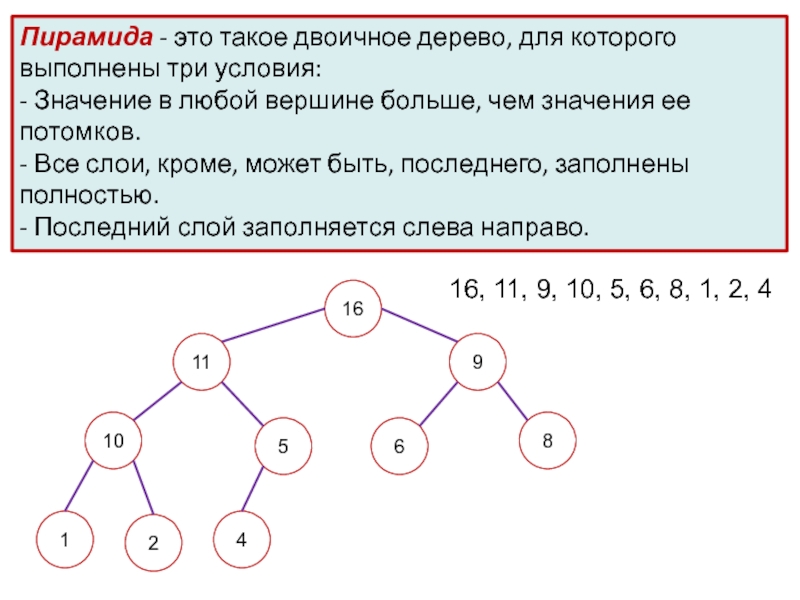
Слайд 9Пирамида - это такое двоичное дерево, для которого выполнены три
условия:
- Значение в любой вершине больше, чем значения ее
потомков. - Все слои, кроме, может быть, последнего, заполнены полностью.
- Последний слой заполняется слева направо.
16, 11, 9, 10, 5, 6, 8, 1, 2, 4
16
11
9
10
5
6
8
4
1
2
Слайд 10СЕТИ. СЕТЕВЫЕ МОДЕЛИ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ
Граф называется взвешенным или сетью,
если каждому его ребру поставлено в соответствие некоторое число (вес).
Взвешенными
графами могут быть схемы в электронике, электрические схемы, схемы компьютерных сетей, карты автомобильных и железных дорог и др. На картах автодорог вершины являются населенными пунктами, ребра — дорогами, а весом — числа, равные расстоянию между населенными пунктами.
Ребрам графа могут соответствовать числа, означающие длину, уклон, запланированное время и другие характеристики.
Слайд 11АЛГОРИТМ КРАСКАЛА
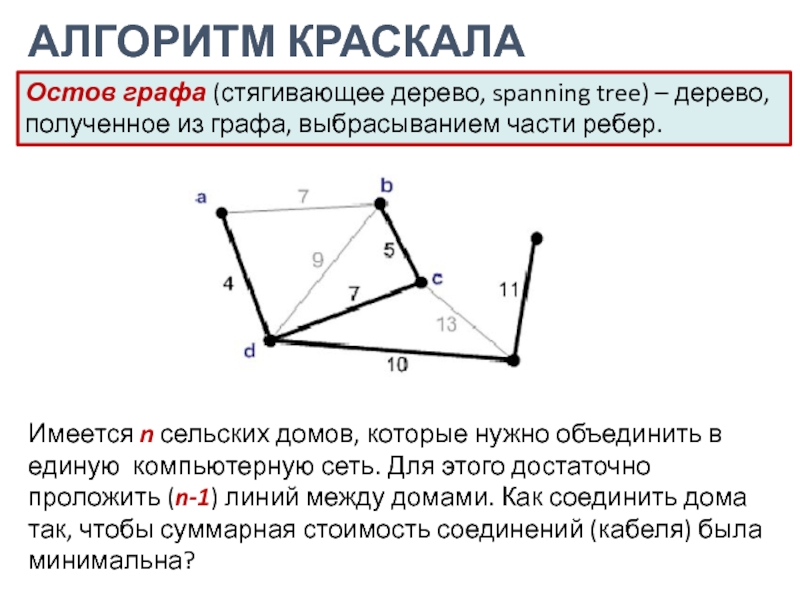
Имеется n сельских домов, которые нужно объединить в
единую компьютерную сеть. Для этого достаточно проложить (n-1) линий между
домами. Как соединить дома так, чтобы суммарная стоимость соединений (кабеля) была минимальна?Остов графа (стягивающее дерево, spanning tree) – дерево, полученное из графа, выбрасыванием части ребер.
Слайд 12ПОСТАНОВКА ЗАДАЧИ
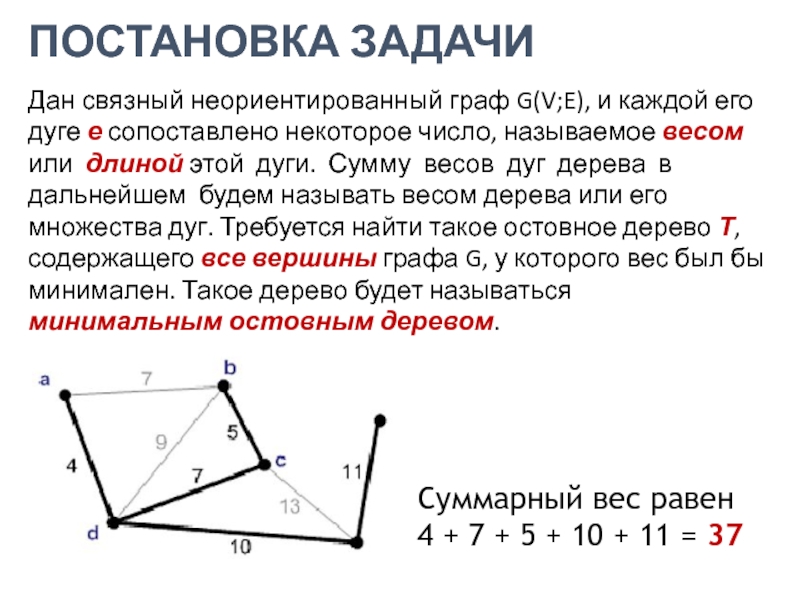
Дан связный неориентированный граф G(V;E), и каждой его дуге
е сопоставлено некоторое число, называемое весом или длиной этой дуги.
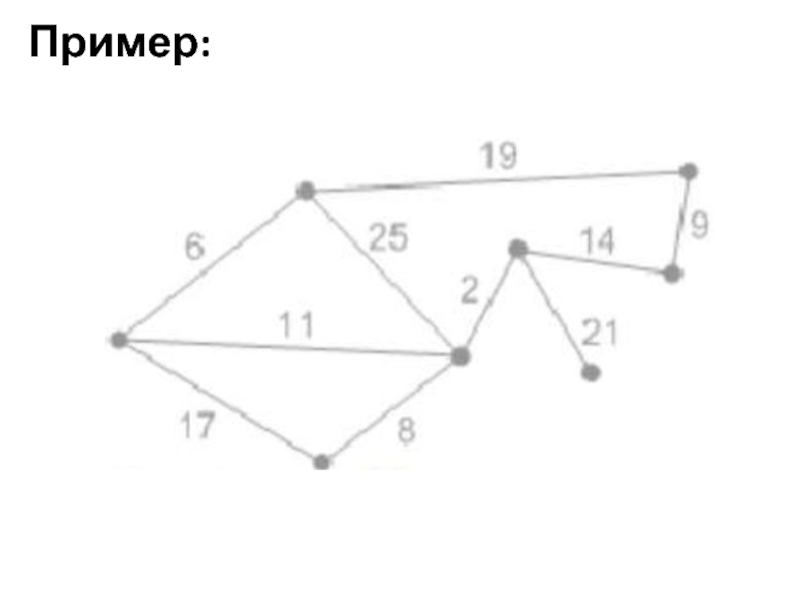
Сумму весов дуг дерева в дальнейшем будем называть весом дерева или его множества дуг. Требуется найти такое остовное дерево Т, содержащего все вершины графа G, у которого вес был бы минимален. Такое дерево будет называться минимальным остовным деревом.Суммарный вес равен
4 + 7 + 5 + 10 + 11 = 37
Слайд 13ОПИСАНИЕ АЛГОРИТМА
1. Вначале текущее множество рѐбер устанавливается пустым.
2. Затем,
пока это возможно, проводится следующая операция:
из всех рѐбер, добавление
которых к уже имеющемуся множеству не вызовет появление в нѐм цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рѐбер больше нет, алгоритм завершѐн. Подграф данного графа, содержащий все его вершины и найденное множество рѐбер, является его остовным деревом минимального веса
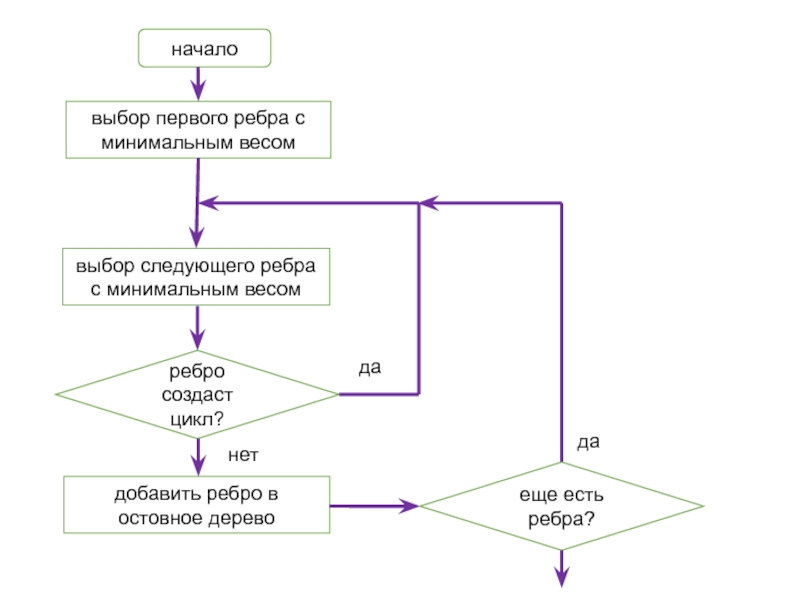
Слайд 14начало
выбор первого ребра с минимальным весом
выбор следующего ребра с минимальным
весом
ребро создаст цикл?
добавить ребро в остовное дерево
еще есть ребра?
нет
да
да
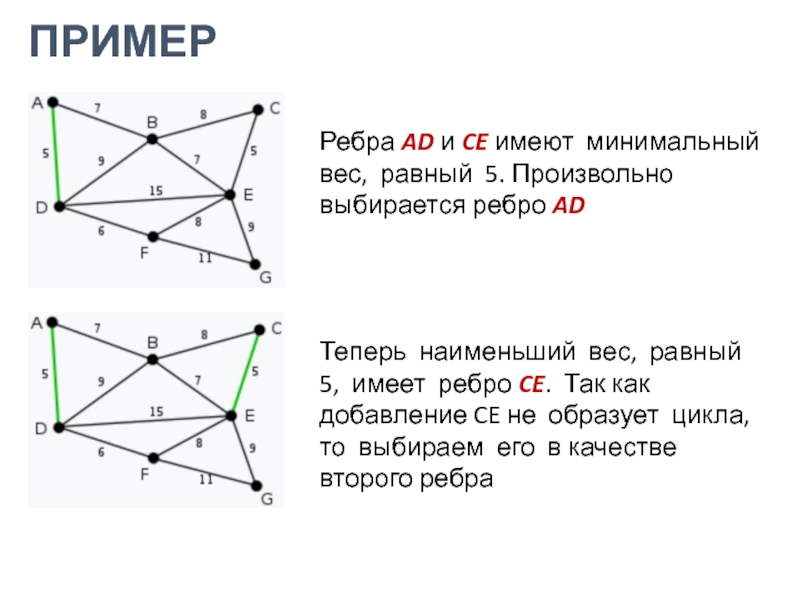
Слайд 15ПРИМЕР
Ребра AD и CE имеют минимальный вес, равный 5. Произвольно
выбирается ребро AD
Теперь наименьший вес, равный 5, имеет ребро CE.
Так как добавление CE не образует цикла, то выбираем его в качестве второго ребраСлайд 16ПРИМЕР
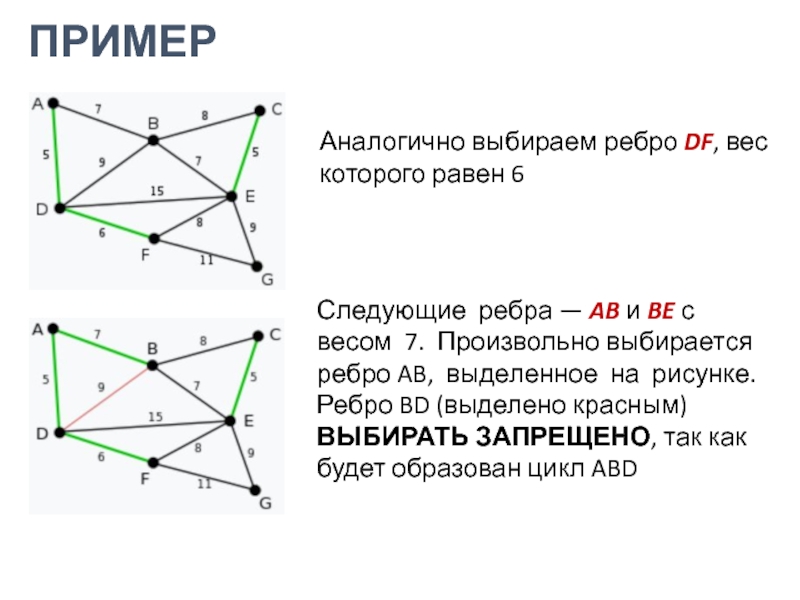
Аналогично выбираем ребро DF, вес которого равен 6
Следующие ребра —
AB и BE с весом 7. Произвольно выбирается ребро AB,
выделенное на рисунке.Ребро BD (выделено красным) ВЫБИРАТЬ ЗАПРЕЩЕНО, так как будет образован цикл ABD
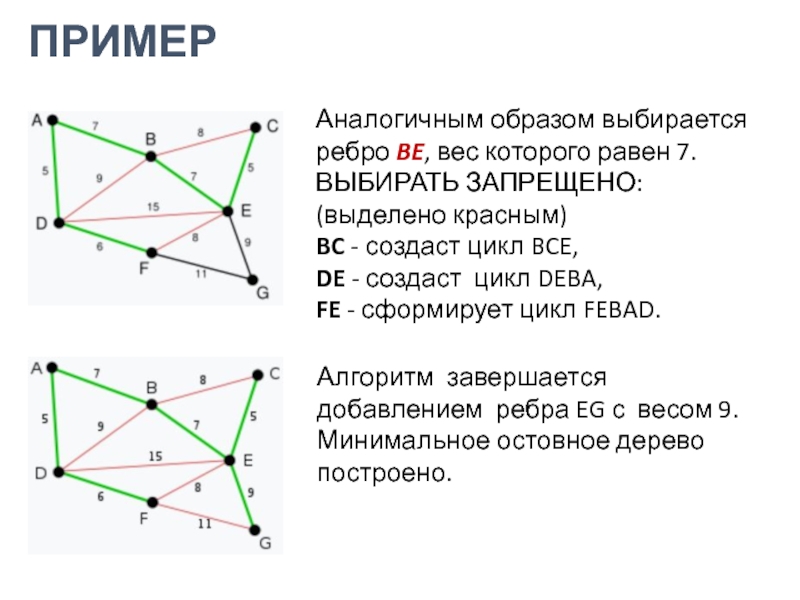
Слайд 17ПРИМЕР
Аналогичным образом выбирается ребро BE, вес которого равен 7.
ВЫБИРАТЬ
ЗАПРЕЩЕНО:
(выделено красным)
BC - создаст цикл BCE,
DE - создаст цикл
DEBA,FE - сформирует цикл FEBAD.
Алгоритм завершается добавлением ребра EG с весом 9. Минимальное остовное дерево построено.
Слайд 23Контрольные вопросы:
1. Что называется деревом в графе?
2. Опишите свойства
деревьев.
4. Что называется бинарным деревом?
5. Что называется цикломатическим
числом графа? Чему равно это число в дереве? Лесе? 6. Какой граф называется сетью?
7. Что называется весом или длиной дуги?
8. Дайте определение остов графа.
9. Дайте определение минимальный остов графа.
10. В чем смысл алгоритма Краскала?