Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве
Содержание
- 1. Векторы в пространстве
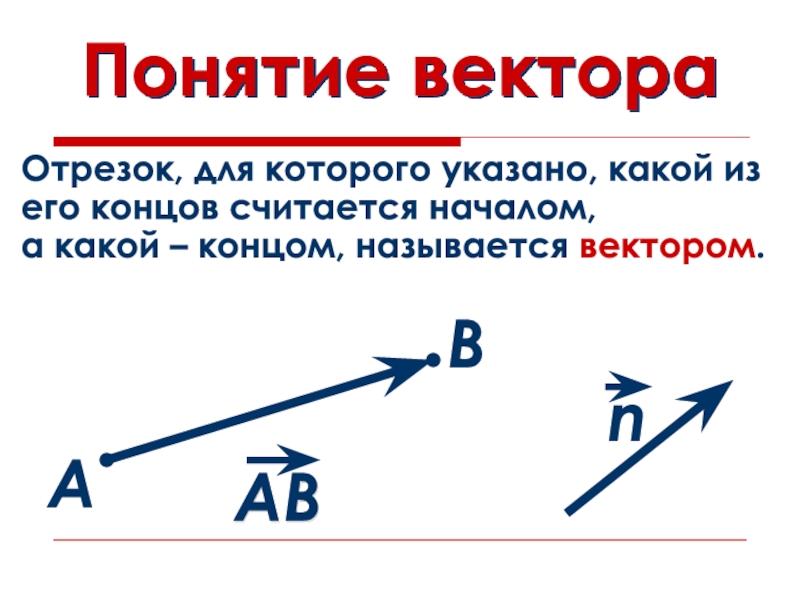
- 2. Понятие вектораАВОтрезок, для которого указано, какой из его концов считается началом,а какой – концом, называется вектором.
- 3. Нулевой векторЛюбая точка на плоскости может рассматриваться как вектор. МТакой вектор называется нулевым.
- 4. Длина вектораАВ
- 5. Коллинеарность векторовДва ненулевых вектора называются коллинеарными, если
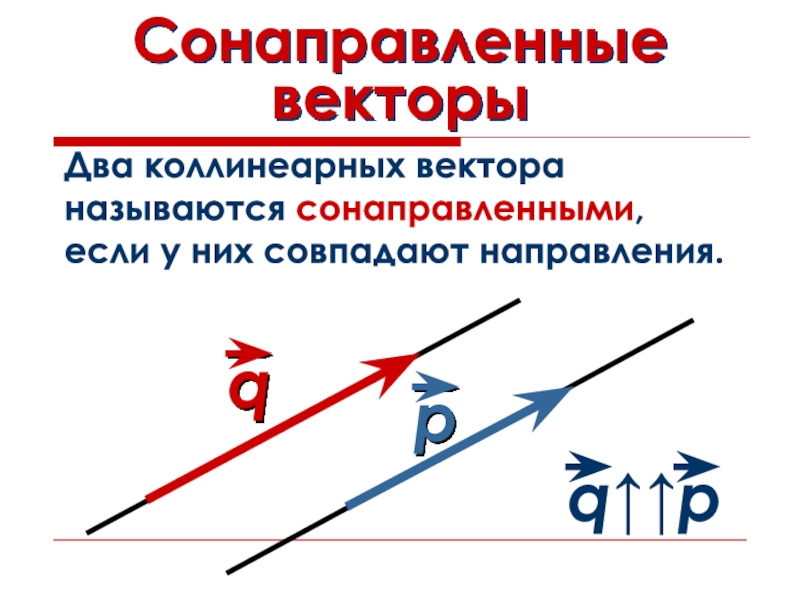
- 6. Сонаправленные векторыДва коллинеарных вектора называются сонаправленными, если у них совпадают направления.
- 7. Противоположно направленные векторыДва коллинеарных вектора называются противоположно направленными, если они не сонаправлены.
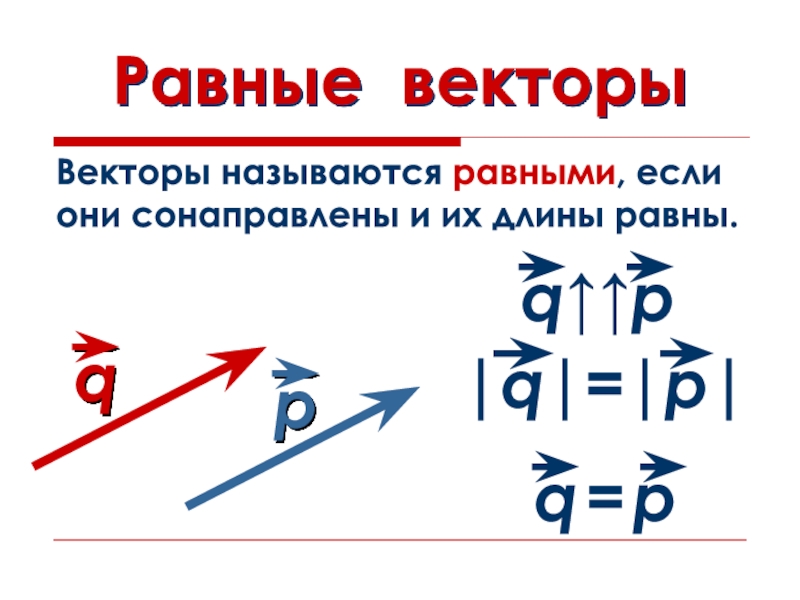
- 8. Равные векторыВекторы называются равными, если они сонаправлены и их длины равны.
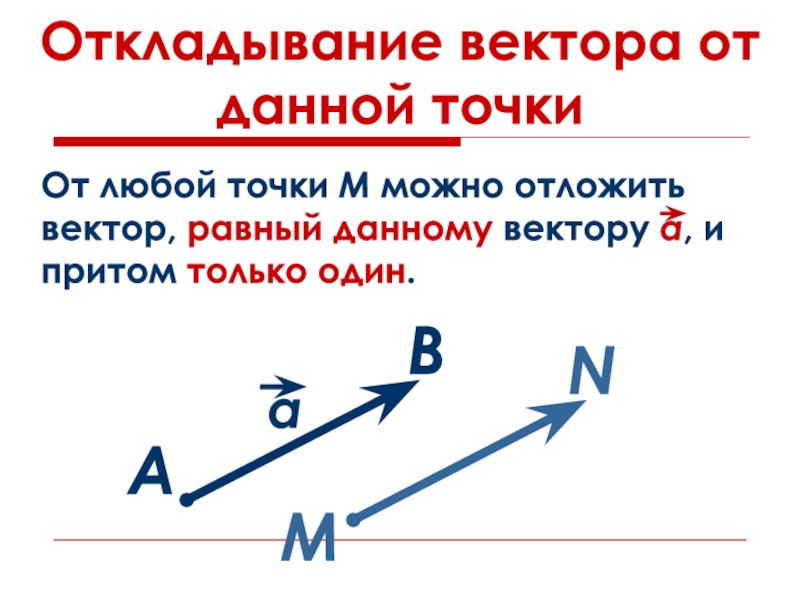
- 9. Откладывание вектора от данной точкиАВМN
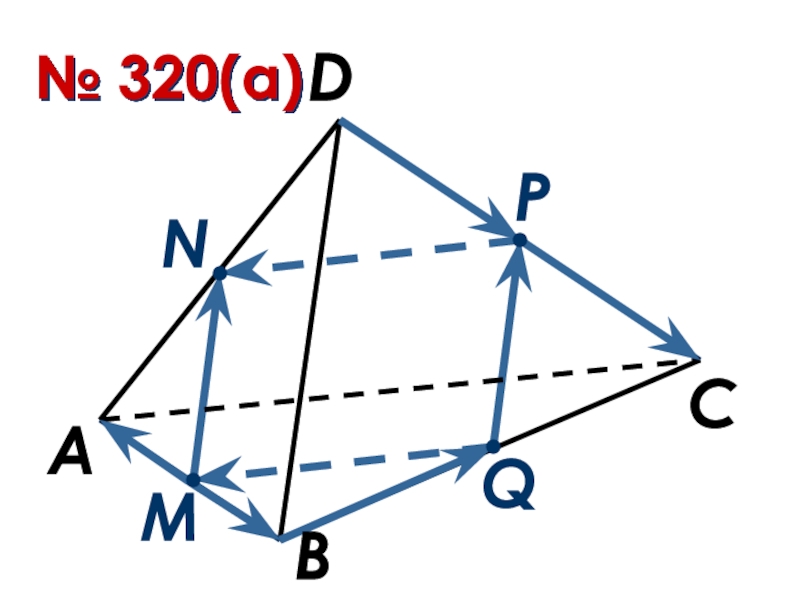
- 10. № 320(а)АВСDMQPN
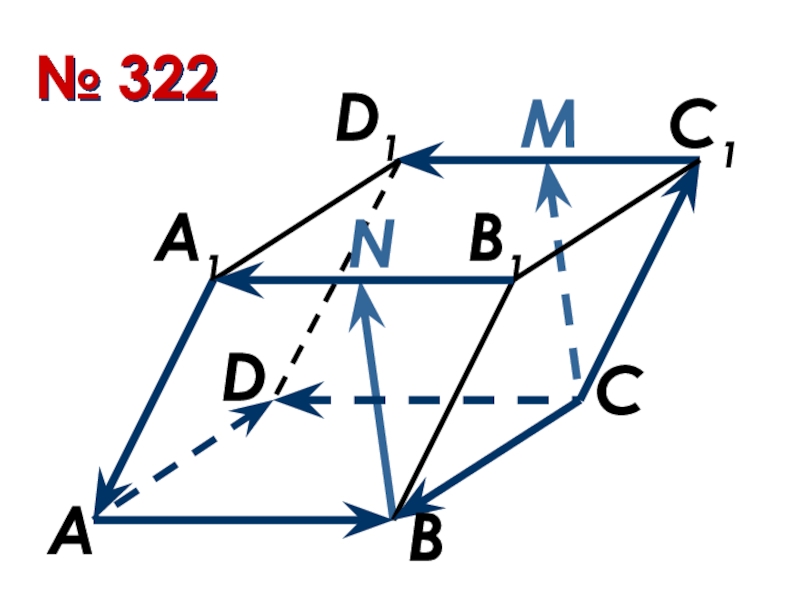
- 11. № 322АВСDА1B1C1D1MN
- 12. Домашнее задание:П. 38, 39, № 320(б)
- 13. СПАСИБО ЗА РАБОТУ!
- 14. Слайд 14
- 15. Скачать презентанцию
Понятие вектораАВОтрезок, для которого указано, какой из его концов считается началом,а какой – концом, называется вектором.
Слайды и текст этой презентации
Слайд 3Нулевой вектор
Любая точка на плоскости может
рассматриваться как вектор.
М
Такой
вектор называется нулевым.
Слайд 5Коллинеарность векторов
Два ненулевых вектора называются
коллинеарными, если они лежат на
одной
прямой или на параллельных прямых.
Слайд 6Сонаправленные векторы
Два коллинеарных вектора
называются сонаправленными,
если у них совпадают
направления.
Слайд 7Противоположно направленные векторы
Два коллинеарных вектора называются
противоположно направленными, если
они
не сонаправлены.
