Слайд 1Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Слайд 2Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
Слайд 3Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
Рассмотрим
функцию y=f(x), заданную на интервале [a;b].
Разделим интервал [a;b] на n
равных частей.
Занумеруем полученные точки xi начиная с нулевого номера
a=xo
Длину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].
Слайд 4Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
Рассмотрим
функцию y=f(x), заданную на интервале [a;b].
Разделим интервал [a;b] на n
равных частей.
Занумеруем полученные точки xi начиная с нулевого номера a=xoДлину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].
В каждой точке xi вычислим значение функции yi =f(xi ).
Полученную пару (xi ; yi ) будем называть узлами функции.
Слайд 6
Однако если возьмем x = – h, тогда получим
Или
.
(2)
Слайд 7
Аналогично взяв x = 2h, получим
или
(3)
Слайд 8
Аналогично взяв x = 2h, получим
или
(3)
Полученные формулы (1) – (3)
называются соответственно правой, левой и центральной разностными формулами численного дифференцирования для первой производной.
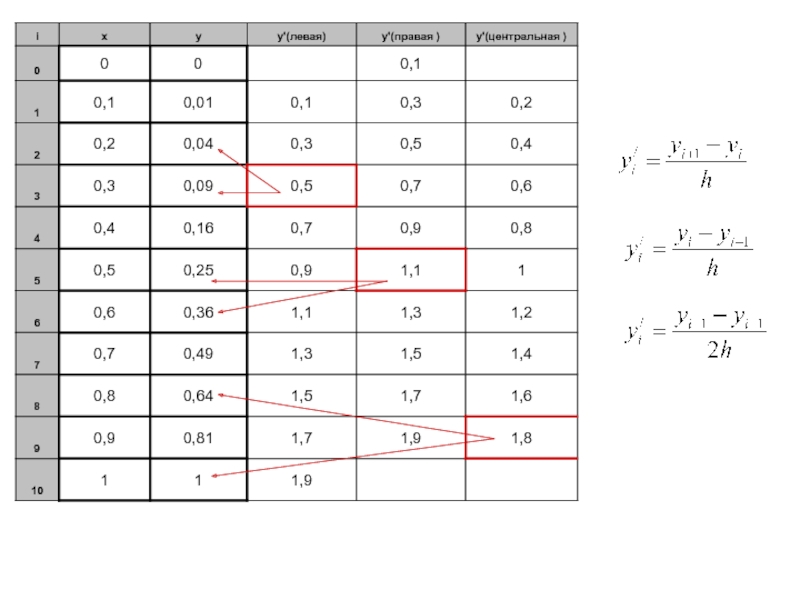
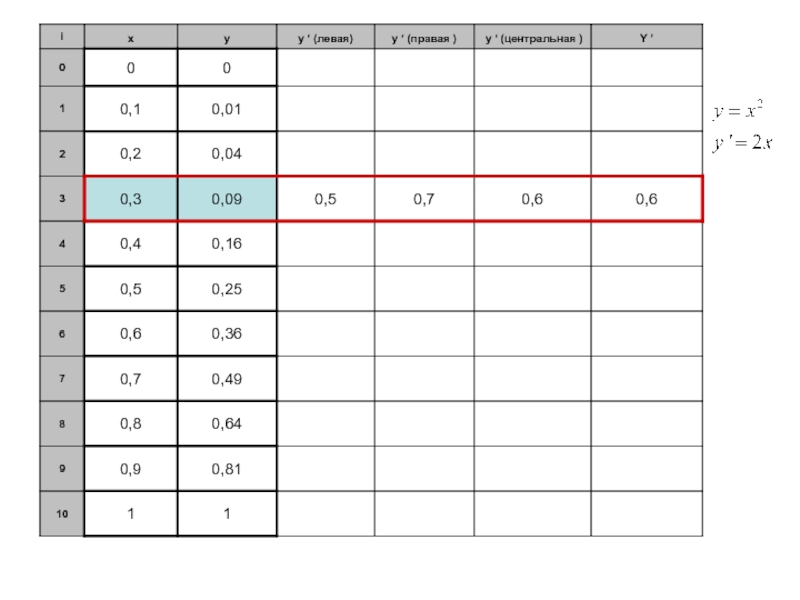
Слайд 9Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с
шагом 0,1.
Найдем первую производную этой функции.
Мы вывели для этого три
различные формулы (1), (2) и (3).
Слайд 12
Аналогично определяются разностные формулы и для старших производных.
Или
Слайд 15
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем
говорить, что функция задана неравномерной сеткой,
если hi =xi +1 –
xi =/= hj=x j+1 – xj
Слайд 16
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем
говорить, что функция задана неравномерной сеткой,
если hi =xi +1 –
xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
Слайд 17
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем
говорить, что функция задана неравномерной сеткой,
если hi =xi +1 –
xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
Слайд 18
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем
говорить, что функция задана неравномерной сеткой,
если hi =xi +1 –
xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
Слайд 19
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем
говорить, что функция задана неравномерной сеткой,
если hi =xi +1 –
xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
- правая производная,
где hi-1=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
Общая формула
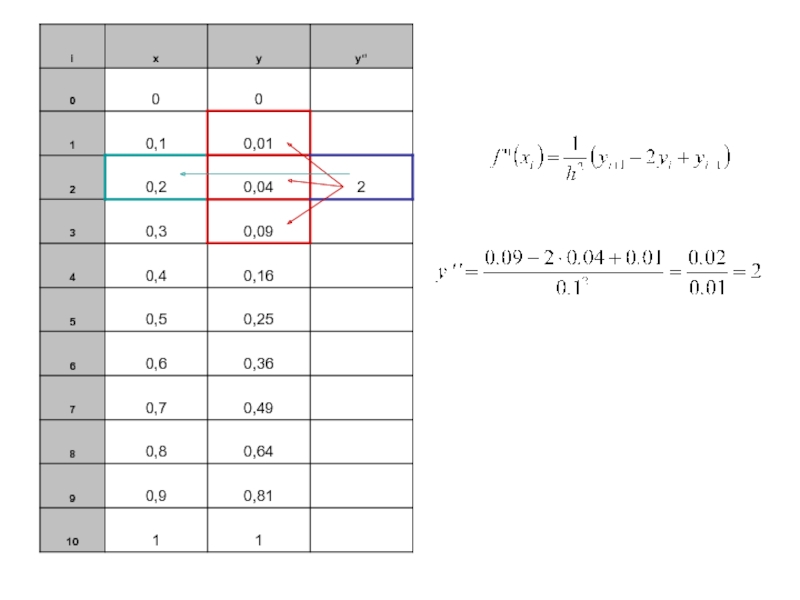
Слайд 21Вторая производная задается формулой
Слайд 22Пример.
Рассмотрим функцию, заданную таблицей
Найти Y/(0.2) и Y//(0.2)
- Правая
Слайд 23Пример.
Рассмотрим функцию, заданную таблицей
Найти Y/(0.2) и Y//(0.2)
- Правая
Y//(0.2)=(0.2*0.25 - (0.2+0.3)*0.04+0.3*0)
/(0.3*0.2 *0.2)=1.67
Погрешность вычисленного значения производной зависит от шага h.
![Численное дифференцированиеРассмотрим функцию y=f(x).По определению производнойИз определения предела получаемприближенное равенствоРассмотрим функцию y=f(x), заданную на интервале [a;b].Разделим интервал](/img/thumbs/8a5926c9ce24df2de62dd0dfbc6f5fac-800x.jpg "Численное дифференцирование
Рассмотрим функцию y = f ( x ).
По определению Численное дифференцированиеРассмотрим функцию y=f(x).По определению производнойИз определения предела получаемприближенное равенствоРассмотрим функцию")
![Численное дифференцированиеРассмотрим функцию y=f(x).По определению производнойИз определения предела получаемприближенное равенствоРассмотрим функцию y=f(x), заданную на интервале [a;b].Разделим интервал](/img/thumbs/d8d9e047a32896206a374bbd3b285b06-800x.jpg "Численное дифференцирование
Рассмотрим функцию y = f ( x ).
По определению Численное дифференцированиеРассмотрим функцию y=f(x).По определению производнойИз определения предела получаемприближенное равенствоРассмотрим функцию")
![Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с шагом 0,1.Найдем первую производную этой функции.Мы вывели](/img/tmb/3/279571/61fb3e4cb39635e50f1d347d849f4c84-800x.jpg "Численное дифференцирование
Рассмотрим функцию y = f ( x ).
По определению Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с шагом")
