Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное моделирование движения и взаимодействия разрывов на декартовых
Содержание
- 1. Численное моделирование движения и взаимодействия разрывов на декартовых
- 2. [1] К.П. Петров. Аэродинамика тел простейших форм.
- 3. [8] A.V. Erofeev, T.A. Lapushkina, S. A.
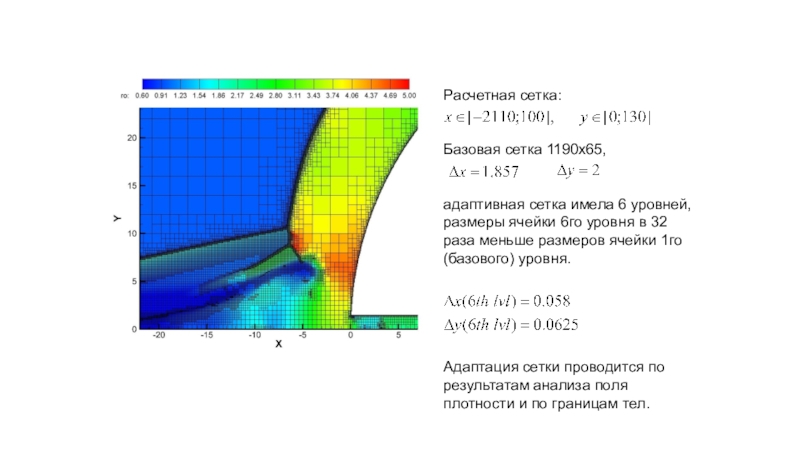
- 4. Расчетная сетка:Базовая сетка 1190х65,адаптивная сетка имела 6
- 5. Распределение давления с линиями тока (стадия увеличения области рециркуляции перед телом)
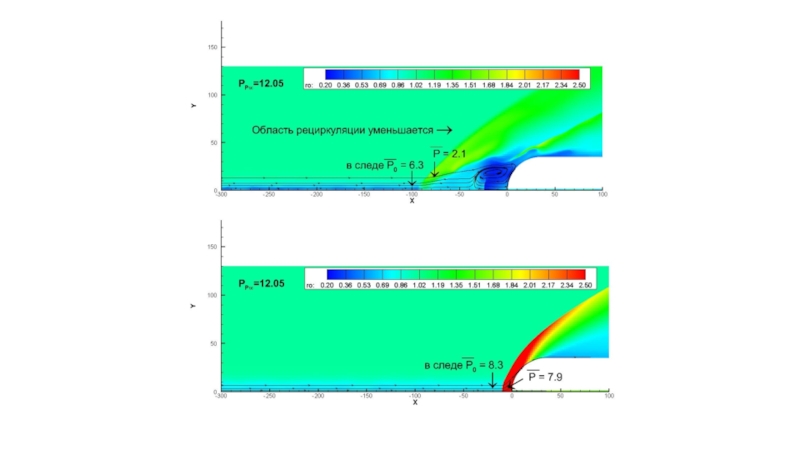
- 6. Распределение давления с линиями тока (продолжение, стадия уменьшения и исчезновения области рециркуляции перед телом)
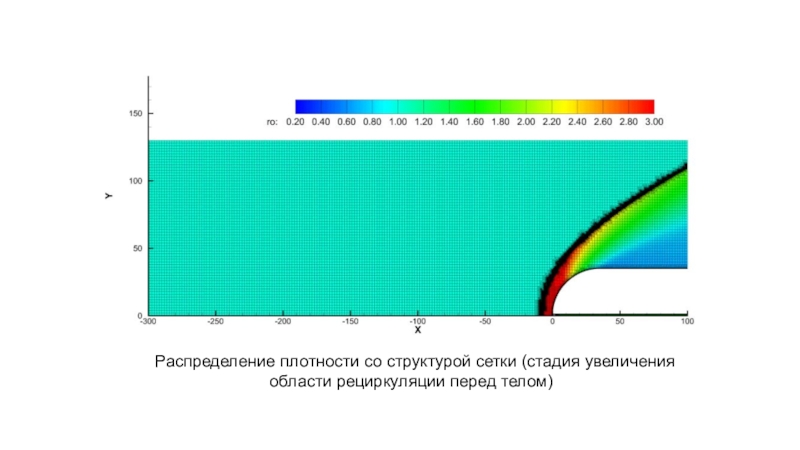
- 7. Распределение плотности со структурой сетки (стадия увеличения области рециркуляции перед телом)
- 8. Распределение плотности со структурой сетки (продолжение, стадия уменьшения и исчезновения области рециркуляции перед телом)
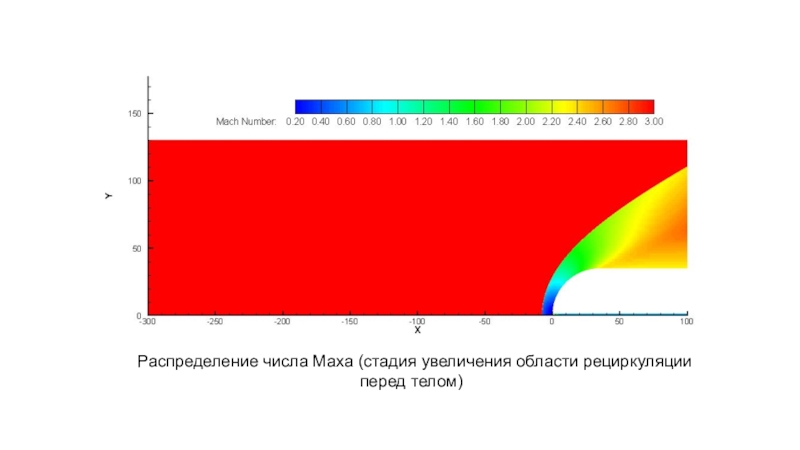
- 9. Распределение числа Маха (стадия увеличения области рециркуляции перед телом)
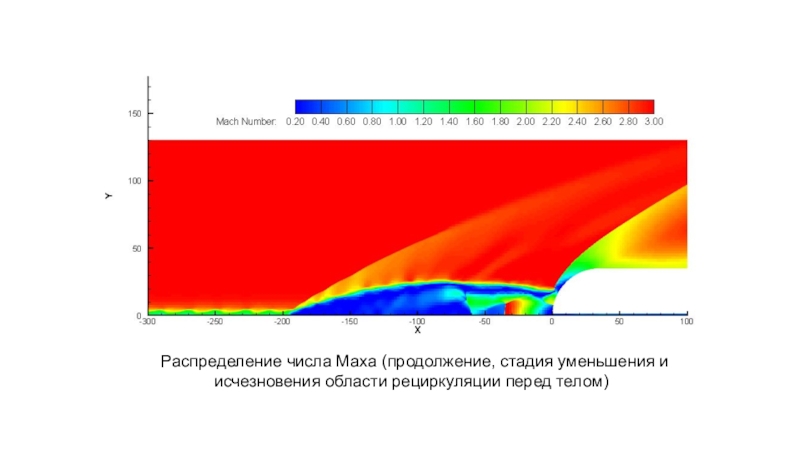
- 10. Распределение числа Маха (продолжение, стадия уменьшения и исчезновения области рециркуляции перед телом)
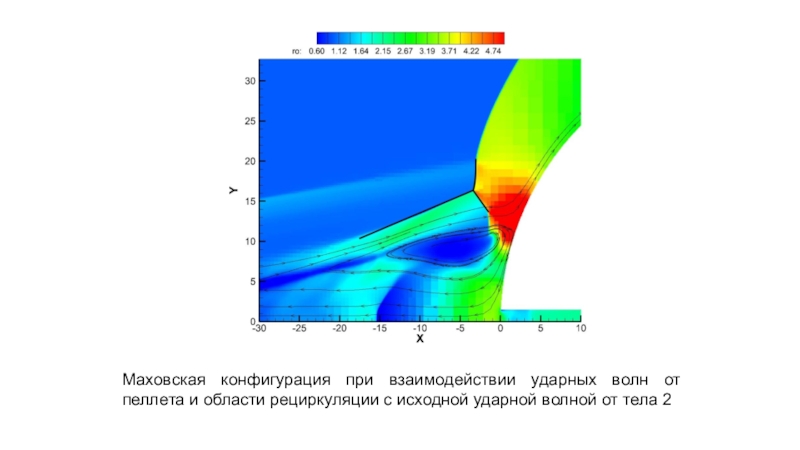
- 11. Маховская конфигурация при взаимодействии ударных волн от
- 12. П.Ю. Георгиевский, В.А. Левин. Сверхзвуковое обтекание тел
- 13. Число Маха из [9] и настоящей работы в следе за пеллетом.Рост числа Маха вдоль оси следа
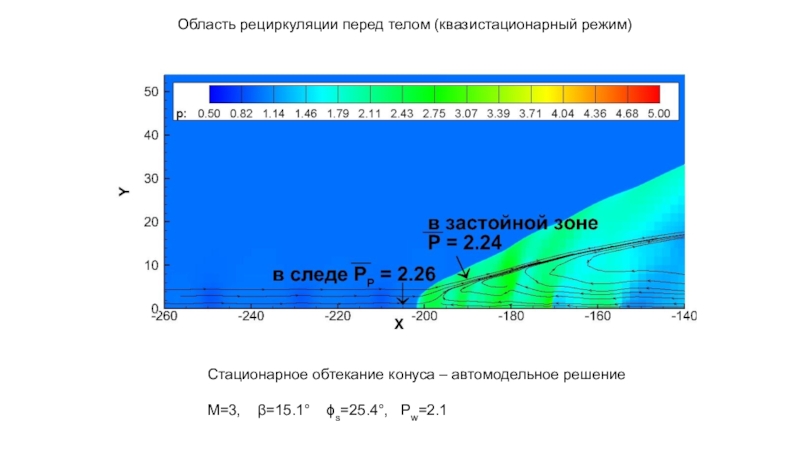
- 14. Область рециркуляции перед телом (квазистационарный режим)Стационарное обтекание
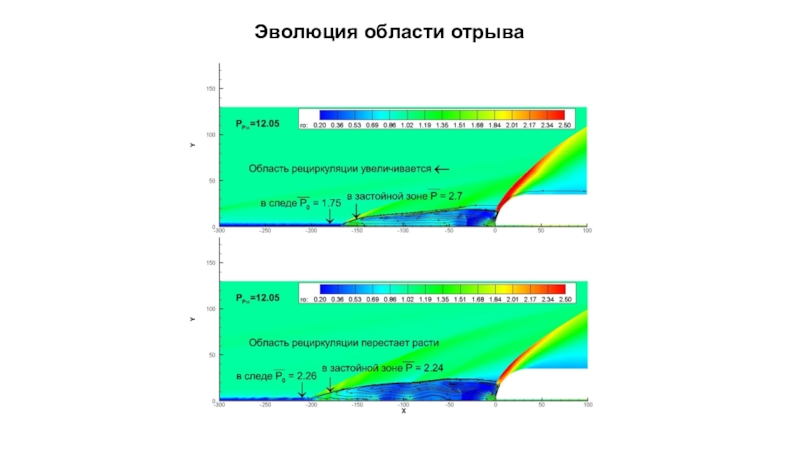
- 15. Эволюция области отрыва
- 16. Слайд 16
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Численное моделирование движения и взаимодействия разрывов на декартовых локально адаптивных
сетках
Слайд 2[1] К.П. Петров. Аэродинамика тел простейших форм. – М.: Издательство
«Факториал»,
1998, 432 с., ISBN 5-88688-014-3;
[2] Кудрявцев В. Н., Черкез
А. Я., Шилов В. А. Исследование сверхзвукового обтекания двухразделяющихся тел. Изв. АН СССР. МЖГ·, 1969, N2.
[3] В.С. Хлебников. Картина сверхзвукового обтекания пары тел и перестройка течения
между ними // Механика жидкости и газа, 1994, № 1. Издательство РАН, Москва;
[4] В.С. Хлебников. Перестройка течения между парой тел, одно из которых расположено в
следе другого, при сверхзвуковом обтекании // Ученые записки ЦАГИ, 1976, т. 7, №3, с.
133-136.
[5] Л.Г. Васенев, Д.А. Внучков, В.И. Звегинцев, С.В. Лукашевич, А.Н. Шиплюк. Измерение
сопротивления двух последовательно расположенных тел вращения при их разделении в
сверхзвуковом потоке //Перспективные технологии самолетостроения в России и в мире:
труды IV-й Всероссийской научно-практической конференции молодых специалистов и
ученых (Новосибирск, 22-24 мая 2012 г.), СибНИА. Новосибирск, 2012. С. 19-24.
[6] Zhukov B. G., Kurakin R. O., Rozov S. I., Sakharov V. A., Beloborodii M. V., Drobyshevski E.
M., Shibanova N. Y. (2002, April). Synchronous EM launch of two bodies with double-barrel
railgun and some peculiarities of their hypersonic flight in air. In Proceedings of the 4-th
Workshop" PA and MHD in Aerospace Applications" (pp. 355-360).
[7] S.Leonov, V.Bityurin, A.Yuriev, S.Pirogov, B.Zhukov. “Problems in Energetic Method of Drag
Reduction and Flow/Flight Control”, AIAA-2003-0035, 41th AIAA Aerospace Sciences Meeting &
Exhibit, Reno, NV, USA, 2003.
[8] A.V. Erofeev, T.A. Lapushkina, S. A. Poniaev, R.O. Kurakin, B.G. Zhukov. "Flow Around
Different Bodies at the Pellet or Plasma Jet Injection", 50th AIAA Aerospace Sciences Meeting
including the New Horizons Forum and Aerospace Exposition, 2012
[9] A.L. Afendikov, Ya. V. Khankhasaeva, A. E. Lusky, I. S. Menshov, K. D. Merkulov.
“Computation and visualization of flows past bodies in mutual motion” // Scientific
Visualization, 2016, T.8. № 4. C. 128-138.
Исследование обтекания последовательно расположенных тел
Слайд 3[8] A.V. Erofeev, T.A. Lapushkina, S. A. Poniaev, R.O. Kurakin,
B.G. Zhukov. "Flow Around Different Bodies at the Pellet or
Plasma Jet Injection", 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2012Тело 1 (пеллет) – цилиндр с d = 2 мм и
l = 2 мм, тело 2 – сферически затупленный цилиндр с D = 70 мм и
L = 100 мм. Диаметр канала – 3 мм.
Скорость набегающего потока М = 3.
Тело 1 вылетает из канала тела 2 со скоростью М = 4 (относительно тела 2)
Слайд 4Расчетная сетка:
Базовая сетка 1190х65,
адаптивная сетка имела 6 уровней, размеры ячейки
6го уровня в 32 раза меньше размеров ячейки 1го (базового)
уровня.Адаптация сетки проводится по результатам анализа поля плотности и по границам тел.
Слайд 6 Распределение давления с линиями тока (продолжение, стадия уменьшения и исчезновения
области рециркуляции перед телом)
Слайд 7 Распределение плотности со структурой сетки (стадия увеличения области рециркуляции перед
телом)
Слайд 8 Распределение плотности со структурой сетки (продолжение, стадия уменьшения и исчезновения
области рециркуляции перед телом)
Слайд 10 Распределение числа Маха (продолжение, стадия уменьшения и исчезновения области рециркуляции
перед телом)
Слайд 11Маховская конфигурация при взаимодействии ударных волн от пеллета и области
рециркуляции с исходной ударной волной от тела 2
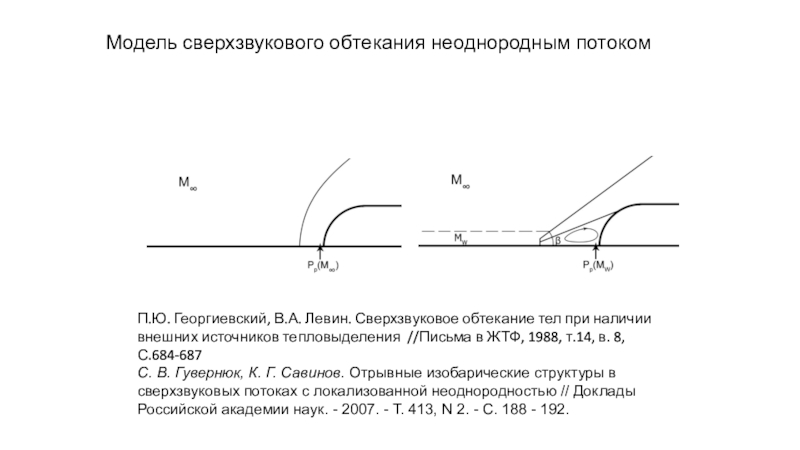
Слайд 12П.Ю. Георгиевский, В.А. Левин. Сверхзвуковое обтекание тел при наличии внешних
источников тепловыделения //Письма в ЖТФ, 1988, т.14, в. 8, С.684-687
С.
В. Гувернюк, К. Г. Савинов. Отрывные изобарические структуры в сверхзвуковых потоках с локализованной неоднородностью // Доклады Российской академии наук. - 2007. - Т. 413, N 2. - С. 188 - 192. Модель сверхзвукового обтекания неоднородным потоком

![Численное моделирование движения и взаимодействия разрывов на декартовых [1] К.П. Петров. Аэродинамика тел простейших форм. – М.: Издательство «Факториал», [1] К.П. Петров. Аэродинамика тел простейших форм. – М.: Издательство «Факториал», 1998, 432 с., ISBN 5-88688-014-3;[2] Кудрявцев](/img/tmb/6/579888/d5f5af71534c8ee99e52f4fd1ea8149c-800x.jpg)
![Численное моделирование движения и взаимодействия разрывов на декартовых [8] A.V. Erofeev, T.A. Lapushkina, S. A. Poniaev, R.O. Kurakin, B.G. [8] A.V. Erofeev, T.A. Lapushkina, S. A. Poniaev, R.O. Kurakin, B.G. Zhukov.](/img/tmb/6/579888/207b5286c42f3d165f738b012ff94fda-800x.jpg)



![Численное моделирование движения и взаимодействия разрывов на декартовых Число Маха из [9] и настоящей работы в следе за пеллетом.Рост числа Маха вдоль оси следа Число Маха из [9] и настоящей работы в следе за пеллетом.Рост числа Маха вдоль оси следа](/img/tmb/6/579888/b80ef5758a24757924da79109e65fff5-800x.jpg)