которую можно задать по своему усмотрению.
Задача решения нелинейного уравнения состоит
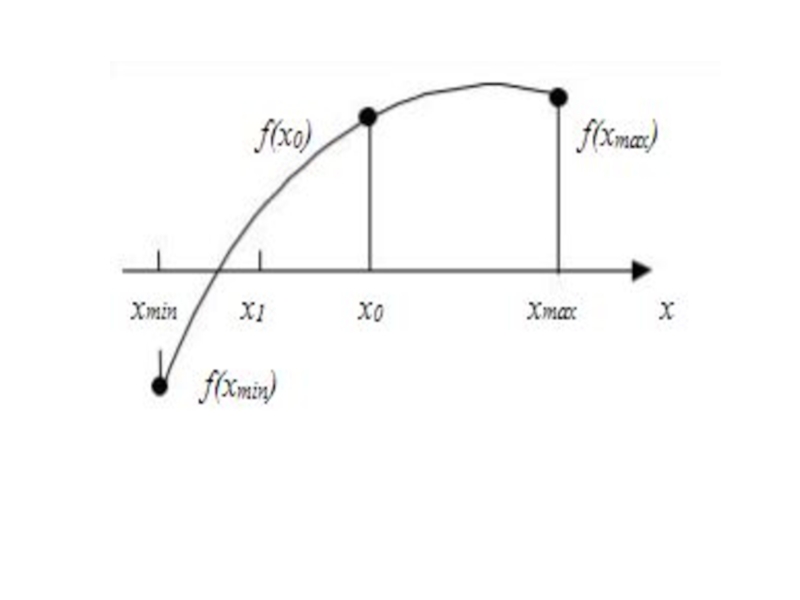
из двух этапов:локализация корней, т.е. определение интервала изоляции (интервала неопределенности), в котором расположен корень;
определение с заданной точностью точности ε приближенного значения корня.














![Численные методы хj– узлы интегрирования Выражение называют квадратурной формулой.Разделим отрезок [a, b] на N равных частей, то хj– узлы интегрирования Выражение называют квадратурной формулой.Разделим отрезок [a, b] на N равных частей, то есть на N элементарных отрезков. Длина каждого элементарного](/img/thumbs/5b222b50db365915c361c20fec404bee-800x.jpg)