Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы ( язык Си )
Содержание
- 1. Численные методы ( язык Си )
- 2. Численные методы (язык Си)Тема 1. Решение уравнений
- 3. Основные понятияТипы решения:аналитическое (точное, в виде формулы)приближенное (неточное)Задача: решить уравнениечисленные методыначальное приближениепри N
- 4. Численные методыИдея: последовательное уточнение решения с помощью
- 5. Есть ли решение на [a, b]?есть решениенет решениянет решения
- 6. Метод дихотомии (деление пополам)Найти середину отрезка [a,b]:
- 7. Метод дихотомии (деления пополам)простотаможно получить решение с
- 8. Метод деления отрезка пополам//----------------------------------------------// BinSolve находит решение
- 9. Как подсчитать число шагов?float BinSolve ( float
- 10. Метод итераций (повторений)Задача:Эквивалентные преобразования:имеет те же решения
- 11. Сходимость итерацийСходящийся итерационный процесс: последовательность
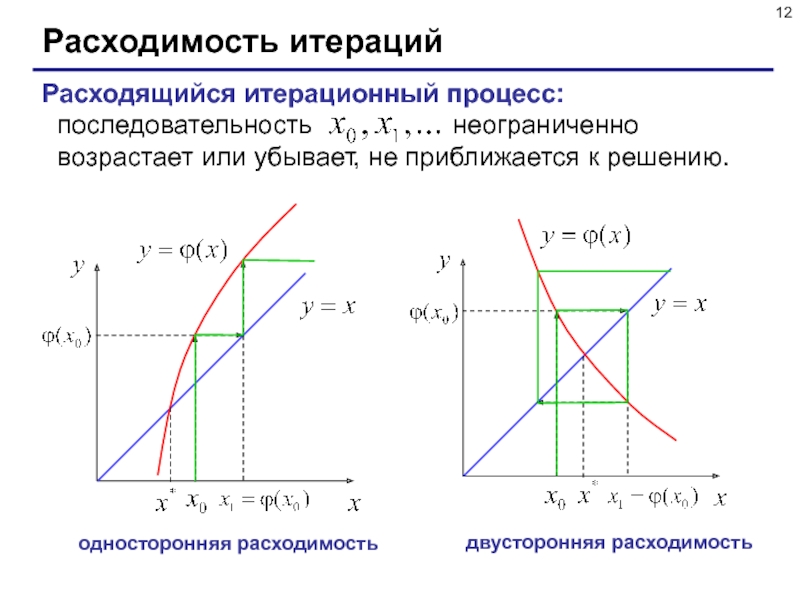
- 12. Расходимость итерацийРасходящийся итерационный процесс: последовательность
- 13. От чего зависит сходимость?сходитсярасходитсяВыводы:сходимость итераций зависит от
- 14. Как выбрать b?наугад, пробовать разные вариантыдля начального приближения x0 пересчитывать на каждом шаге, например:
- 15. Метод итераций (программа)//----------------------------------------------// Iter решение уравнения методом
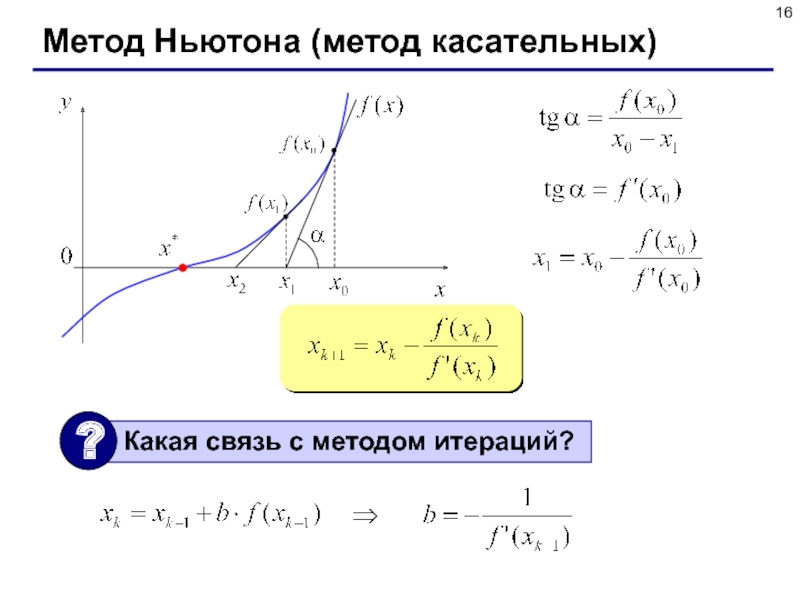
- 16. Метод Ньютона (метод касательных)
- 17. Метод Ньютона (программа)//----------------------------------------------// Newton решение уравнения методом
- 18. Метод Ньютонабыстрая (квадратичная) сходимость – ошибка на
- 19. Численные методы (язык Си)Тема 2. Вычисление площади (интеграла)
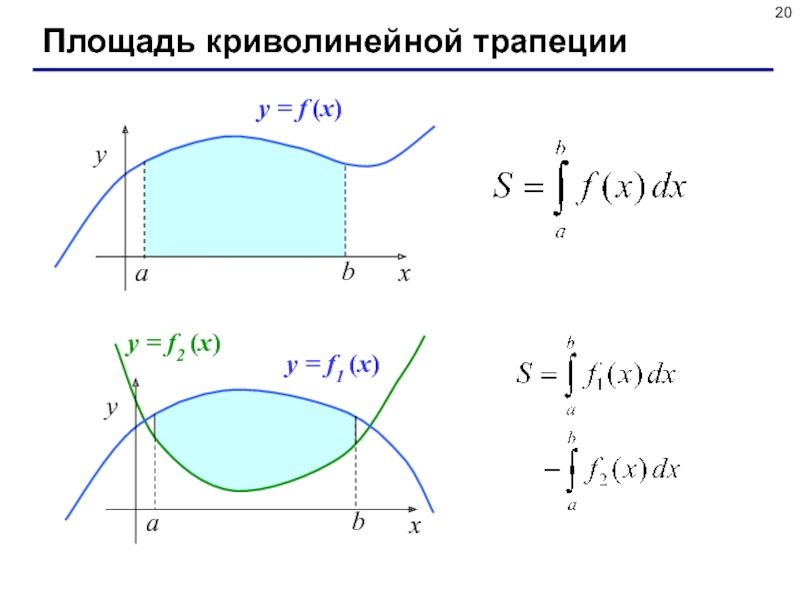
- 20. Площадь криволинейной трапеции
- 21. Метод (левых) прямоугольниковy = f1 (x)y =
- 22. Метод (правых) прямоугольниковxyx2x1y = f1 (x)y =
- 23. Метод (средних) прямоугольниковxyx2x1y = f1 (x)y =
- 24. Метод трапецийxyx2x1y = f1 (x)y = f2
- 25. Метод Монте-КарлоПрименение: вычисление площадей сложных фигур (трудно
- 26. Метод Монте-КарлоВписываем сложную фигуру в другую фигуру,
- 27. Численные методы (язык Си)Тема 3. Вычисление длины кривой
- 28. Длина кривойТочное решение:нужна формула для производнойсложно взять интегралПриближенное решение:
- 29. Длина кривой//-----------------------------------------// CurveLen вычисление длины кривой// Вход:
- 30. Численные методыТема 4. Оптимизация
- 31. Найти x, при котором
- 32. Локальные и глобальные минимумыглобальный минимумЗадача: найти глобальный
- 33. Минимум функции одной переменнойДано: на интервале [a,b]
- 34. Минимум функции одной переменнойКоэффициент сжатия:Самое быстрое сжатие:придолжно
- 35. Отношение «золотого сечения»Идея: выбрать c и d
- 36. Метод «золотого сечения»//----------------------------------------------// Gold поиск минимума функции
- 37. Функции нескольких переменныхПроблемы:нет универсальных алгоритмов поиска глобального
- 38. Метод покоординатного спускаИдея:выбираем начальную точкубудем менять только
- 39. Градиентные методыГрадиент – это вектор, показывающий направление
- 40. Метод случайного поискаИдея:выбираем начальную точкупробуем сделать шаг
- 41. Конец фильма
- 42. Скачать презентанцию
Численные методы (язык Си)Тема 1. Решение уравнений
Слайды и текст этой презентации
Слайд 1Численные методы
(язык Си)
Решение уравнений
Вычисление площади (интеграла)
Вычисление длины кривой
Оптимизация
Слайд 3Основные понятия
Типы решения:
аналитическое (точное, в виде формулы)
приближенное (неточное)
Задача: решить уравнение
численные
методы
Слайд 4Численные методы
Идея: последовательное уточнение решения с помощью некоторого алгоритма.
Область применения:
когда найти точное решение невозможно или крайне сложно.
можно найти хоть
какое-то решениево многих случаях можно оценить ошибку (то есть можно найти решение с заданной точностью)
нельзя найти точное решение
невозможно исследовать решение при изменении параметров
большой объем вычислений
иногда сложно оценить ошибку
нет универсальных методов
![Есть ли решение на [a, b]?есть решениенет решениянет решения](/img/thumbs/a696caac232a110bb9929ffc16610fbc-800x.jpg "Численные методы ( язык Си ) Есть ли решение на [a, b]?есть решениенет решениянет решения")
Слайд 6Метод дихотомии (деление пополам)
Найти середину отрезка [a,b]:
c
= (a + b) / 2;
Если f(c)*f(a)
интервала
b = c;Если f(c)*f(a)≥ 0, сдвинуть левую границу интервала a = c;
Повторять шаги 1-3, пока не будет b – a ≤ .
![Метод дихотомии (деление пополам)Найти середину отрезка [a,b]: c = (a + b) / 2;Если](/img/thumbs/eb23d74de6369ac511533eaf5b9bf049-800x.jpg "Численные методы ( язык Си ) Метод дихотомии (деление пополам)Найти середину отрезка [a,b]: c = (a + b) / 2;Если f(c)*f(a)")
Слайд 7Метод дихотомии (деления пополам)
простота
можно получить решение с заданной точностью (в
пределах точности машинных вычислений)
нужно знать интервал [a, b]
на интервале [a,
b] должно быть только одно решениебольшое число шагов для достижения высокой точности
только для функций одной переменной
Слайд 8Метод деления отрезка пополам
//----------------------------------------------
// BinSolve находит решение на [a,b]
//
методом деления отрезка пополам
// Вход: a,
b – границы интервала, a < b// eps - точность решения
// Выход: x – решение уравнения f(x)=0
//----------------------------------------------
float BinSolve ( float a, float b, float eps )
{
float c;
while ( b - a > eps )
{
c = (a + b) / 2;
if ( f(a)*f(c) < 0 )
b = c;
else a = c;
}
return (a + b) / 2;
}
float f ( float x )
{
return x*x – 5;
}
![Метод деления отрезка пополам//----------------------------------------------// BinSolve находит решение на [a,b]// методом деления отрезка пополам](/img/thumbs/5f73e4158569d28672e0c27edd35f19b-800x.jpg "Численные методы ( язык Си ) Метод деления отрезка пополам//----------------------------------------------// BinSolve находит решение на [a,b]//")
Слайд 9Как подсчитать число шагов?
float BinSolve ( float a, float b,
float
eps, int &n ){
float c;
n = 0;
while ( b - a > eps )
{
c = (a + b) / 2;
if ( f(a)*f(c) < 0 )
b = c;
else a = c;
n ++;
}
return (a + b) / 2;
}
int &n
n = 0;
n ++;
значение переменной меняется внутри функции
Слайд 10Метод итераций (повторений)
Задача:
Эквивалентные преобразования:
имеет те же решения при
Идея решения:
– начальное
приближение (например, с графика)
Проблемы:
как лучше выбрать ?
всегда ли
так можно найти решение?
Слайд 11Сходимость итераций
Сходящийся итерационный процесс: последовательность
приближается (сходится) к точному решению.
односторонняя сходимость
двусторонняя
сходимость
Слайд 12Расходимость итераций
Расходящийся итерационный процесс: последовательность
неограниченно возрастает или убывает, не приближается
к решению.односторонняя расходимость
двусторонняя расходимость
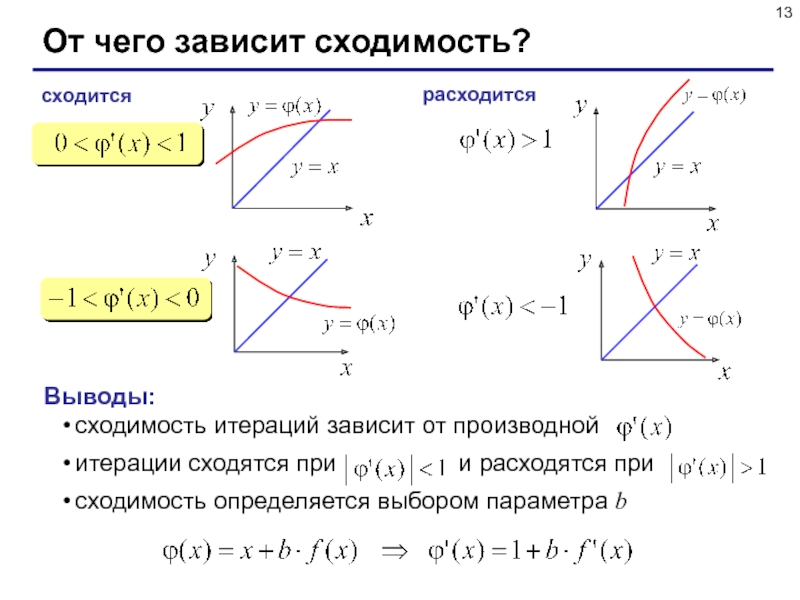
Слайд 13От чего зависит сходимость?
сходится
расходится
Выводы:
сходимость итераций зависит от производной
итерации сходятся при
и расходятся
присходимость определяется выбором параметра b
Слайд 14Как выбрать b?
наугад, пробовать разные варианты
для начального приближения x0
пересчитывать
на каждом шаге, например:
Слайд 15Метод итераций (программа)
//----------------------------------------------
// Iter решение уравнения методом итераций
// Вход: x
– начальное приближение
// b - параметр
//
eps - точность решения// Выход: решение уравнения f(x)=0
// n - число шагов
////----------------------------------------------
float Iter ( float x, float b, float eps, int &n)
{
float dx;
n = 0;
while ( 1 ) {
dx = b*f(x);
x = x + dx;
if ( fabs(dx) < eps ) break;
n ++;
if ( n > 100 ) break;
}
return x;
}
аварийный выход (итерации расходятся)
нормальный выход
Слайд 17Метод Ньютона (программа)
//----------------------------------------------
// Newton решение уравнения методом Ньютона
// Вход: x
– начальное приближение
// eps - точность решения
//
Выход: решение уравнения f(x)=0// n - число шагов
//----------------------------------------------
float Newton ( float x, float eps, int &n)
{
float dx;
n = 0;
while ( 1 ) {
dx = f(x) / df(x);
x = x - dx;
if ( fabs(dx) < eps ) break;
n ++;
if ( n > 100 ) break;
}
return x;
}
float f ( float x ) {
return 3*x*x*x+2*x+5;
}
float df ( float x ) {
return 9*x*x + 2;
}
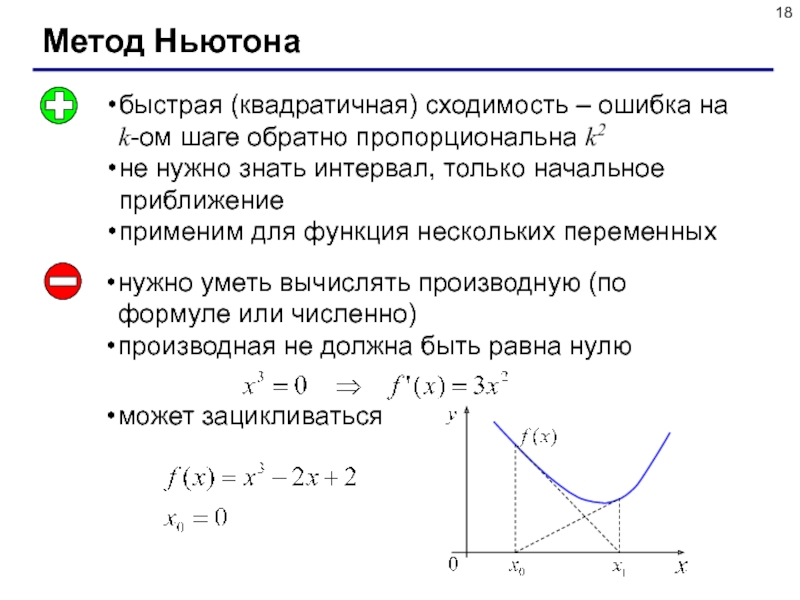
Слайд 18Метод Ньютона
быстрая (квадратичная) сходимость – ошибка на k-ом шаге обратно
пропорциональна k2
не нужно знать интервал, только начальное приближение
применим для функция
нескольких переменныхнужно уметь вычислять производную (по формуле или численно)
производная не должна быть равна нулю
может зацикливаться
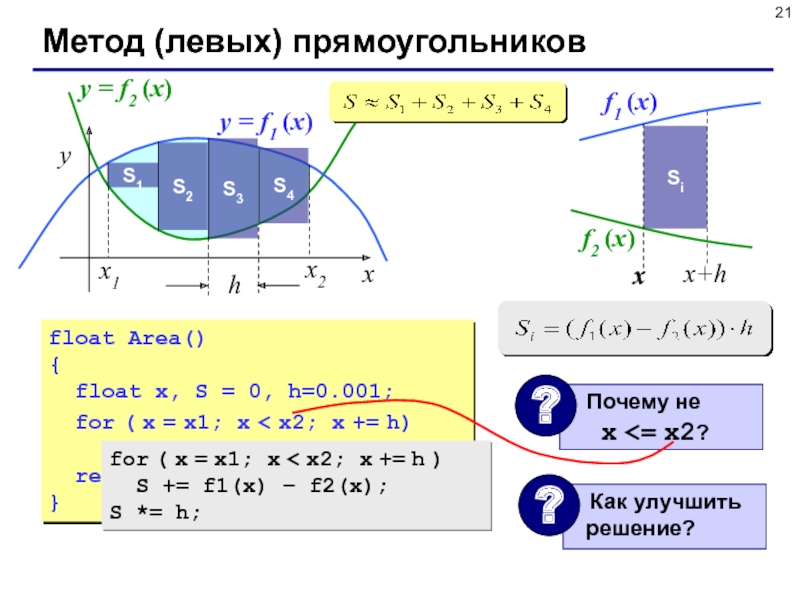
Слайд 21Метод (левых) прямоугольников
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
float Area()
{
float x, S = 0, h=0.001;
for ( x =
x1; x < x2; x += h)S += h*(f1(x) – f2(x));
return S;
}
for ( x = x1; x < x2; x += h )
S += f1(x) – f2(x);
S *= h;
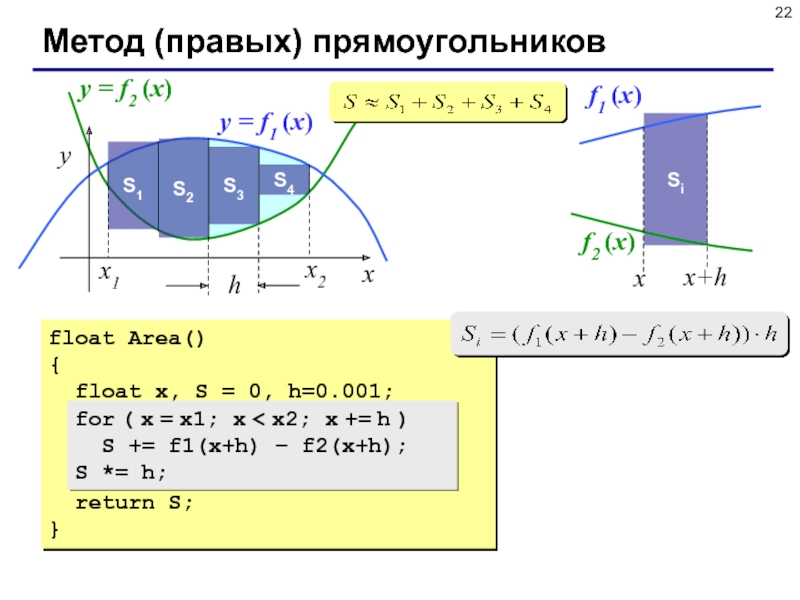
Слайд 22Метод (правых) прямоугольников
x
y
x2
x1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
float Area()
{
float x, S = 0, h=0.001;
for ( x =
x1; x < x2; x += h)S += h*(f1(x+h) – f2(x+h));
return S;
}
for ( x = x1; x < x2; x += h )
S += f1(x+h) – f2(x+h);
S *= h;
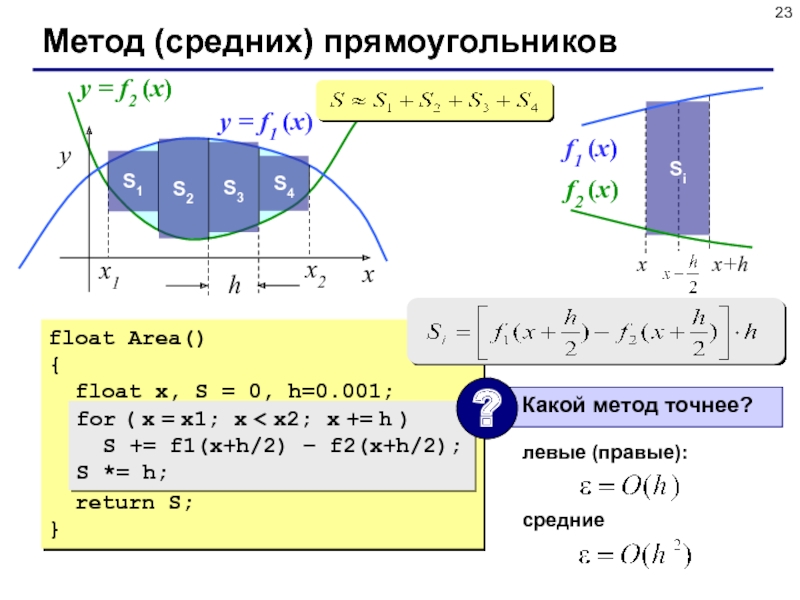
Слайд 23Метод (средних) прямоугольников
x
y
x2
x1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
float Area()
{
float x, S = 0, h=0.001;
for ( x =
x1; x < x2; x += h)S += h*(f1(x+h) – f2(x+h));
return S;
}
for ( x = x1; x < x2; x += h )
S += f1(x+h/2) – f2(x+h/2);
S *= h;
левые (правые):
средние
Слайд 24Метод трапеций
x
y
x2
x1
y = f1 (x)
y = f2 (x)
for ( x
= x1; x < x2; x += h )
S += f1(x) – f2(x) +f1(x+h) – f2(x+h);
S *= h/2;
S =( f1(x1) - f2(x1)
+ f1(x2) - f2(x2) )/2.;
for ( x = x1+h; x < x2; x += h )
S += f1(x) – f2(x);
S *= h;
Слайд 25Метод Монте-Карло
Применение: вычисление площадей сложных фигур (трудно применить другие методы).
Требования:
необходимо уметь достаточно просто определять, попала ли точка (x, y)
внутрь фигуры.Пример: заданы 100 кругов (координаты центра, радиусы), которые могу пересекаться. Найти площадь области, перекрытой кругами.
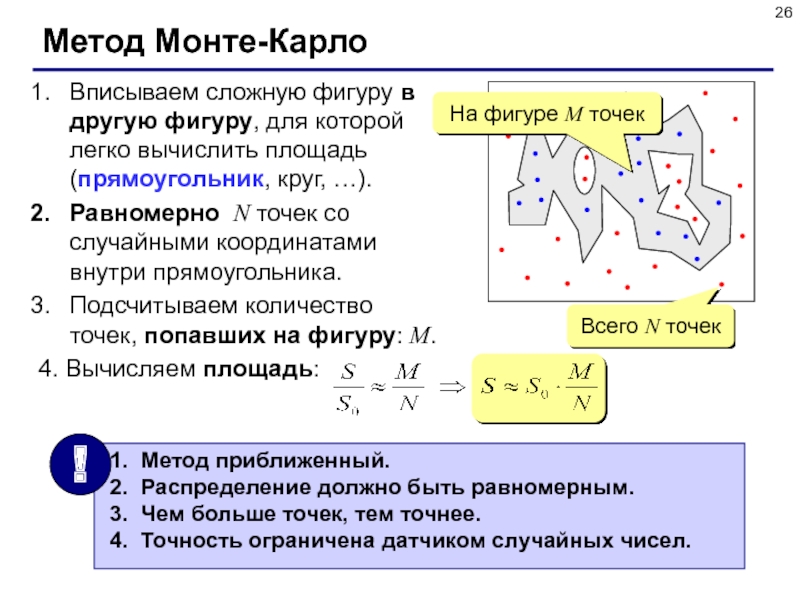
Слайд 26Метод Монте-Карло
Вписываем сложную фигуру в другую фигуру, для которой легко
вычислить площадь (прямоугольник, круг, …).
Равномерно N точек со случайными
координатами внутри прямоугольника. Подсчитываем количество точек, попавших на фигуру: M.
4. Вычисляем площадь:
Всего N точек
На фигуре M точек
Метод приближенный.
Распределение должно быть равномерным.
Чем больше точек, тем точнее.
Точность ограничена датчиком случайных чисел.
!
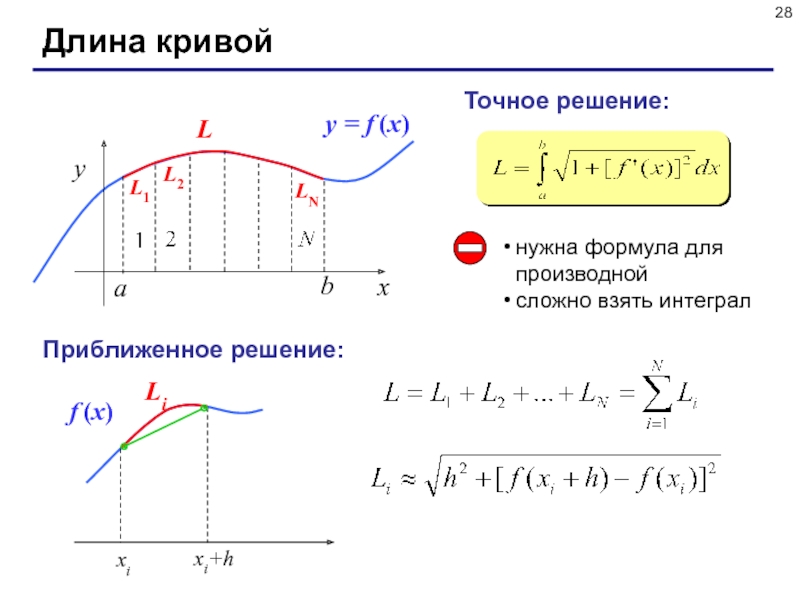
Слайд 28Длина кривой
Точное решение:
нужна формула для производной
сложно взять интеграл
Приближенное решение:
Слайд 29Длина кривой
//-----------------------------------------
// CurveLen вычисление длины кривой
// Вход: a, b –
границы интервала
// Выход: длина кривой y = f(x) на [a,b]
//-----------------------------------------
float
CurveLen ( float a, float b ){
float x, dy, h = 0.0001,
h2 = h*h, L = 0;
for ( x = a; x < b; x += h ) {
dy = f(x+h) - f(x);
L += sqrt(h2 + dy*dy);
}
return L;
}
Слайд 31Найти x, при котором
или
при заданных ограничениях.Основные понятия
Оптимизация – поиск оптимального (наилучшего в некотором смысле) решения.
Цель: определить значения неизвестных параметров, при которых заданная функция достигает минимума (затраты) или максимума (доходы).
Ограничения – условия, которые делают задачу осмысленной.
или
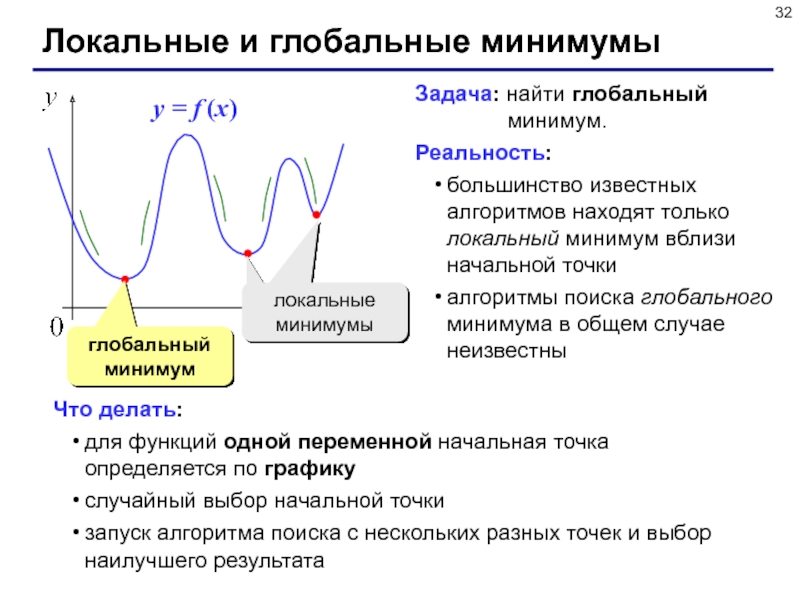
Слайд 32Локальные и глобальные минимумы
глобальный минимум
Задача: найти глобальный
минимум.
Реальность:
большинство известных алгоритмов находят только
локальный минимум вблизи начальной точкиалгоритмы поиска глобального минимума в общем случае неизвестны
Что делать:
для функций одной переменной начальная точка определяется по графику
случайный выбор начальной точки
запуск алгоритма поиска с нескольких разных точек и выбор наилучшего результата
Слайд 33Минимум функции одной переменной
Дано: на интервале [a,b] функция непрерывна и
имеет единственный минимум.
Найти: x*
y = f (x)
Принцип сжатия интервала:
![Минимум функции одной переменнойДано: на интервале [a,b] функция непрерывна и имеет единственный минимум.Найти: x*y = f (x)Принцип](/img/thumbs/c05dfc6a09b48c48a9edb2ccea0043d5-800x.jpg "Численные методы ( язык Си ) Минимум функции одной переменнойДано: на интервале [a,b] функция непрерывна и имеет")
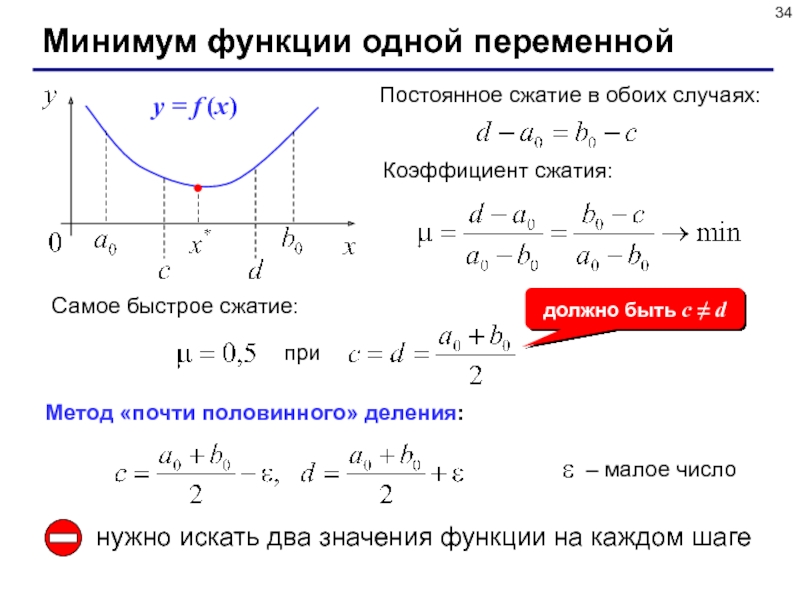
Слайд 34Минимум функции одной переменной
Коэффициент сжатия:
Самое быстрое сжатие:
при
должно быть c
d
Метод «почти половинного» деления:
– малое число
нужно искать два значения функции
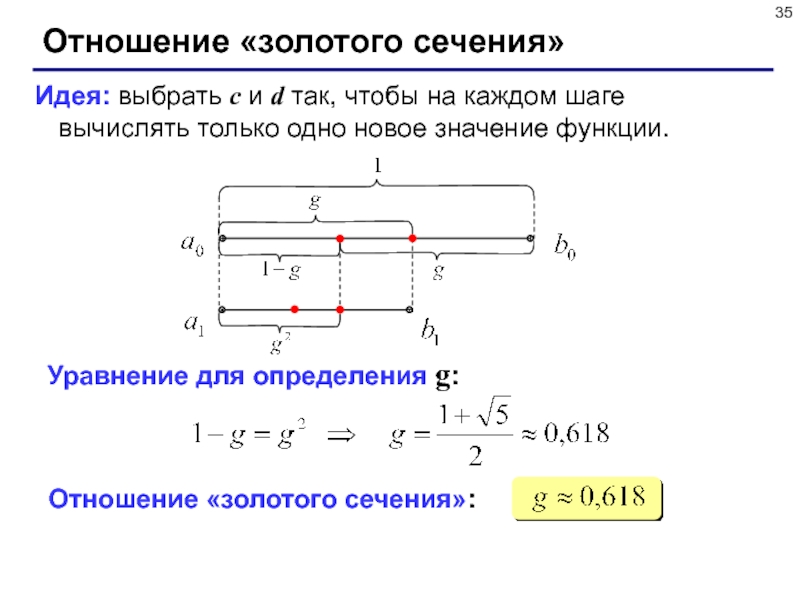
на каждом шаге
Слайд 35Отношение «золотого сечения»
Идея: выбрать c и d так, чтобы на
каждом шаге вычислять только одно новое значение функции.
Уравнение для
определения g:Отношение «золотого сечения»:
Слайд 36Метод «золотого сечения»
//----------------------------------------------
// Gold поиск минимума функции («золотое сечение»)
// Вход:
a, b – границы интервала
// eps –
точность // Выход: x, при котором f(x) имеет минимум // на интервале [a,b]
//----------------------------------------------
float Gold (float a, float b, float eps )
{
float x1, x2, g = 0.618034, R = g*(b - a);
while ( fabs(b-a) > eps ) {
x1 = b - R; x2 = a + R;
if ( f(x1) > f(x2) ) a = x1;
else b = x2;
R *= g;
}
return (a + b) /2.;
}
Слайд 37Функции нескольких переменных
Проблемы:
нет универсальных алгоритмов поиска глобального минимума
неясно, как выбрать
начальное приближение (зависит от задачи и интуиции)
Подходы:
методы локальной оптимизации (результат
зависит от выбора начального приближения)случайный поиск (без гарантии)
методы глобальной оптимизации (для особых классов функций)
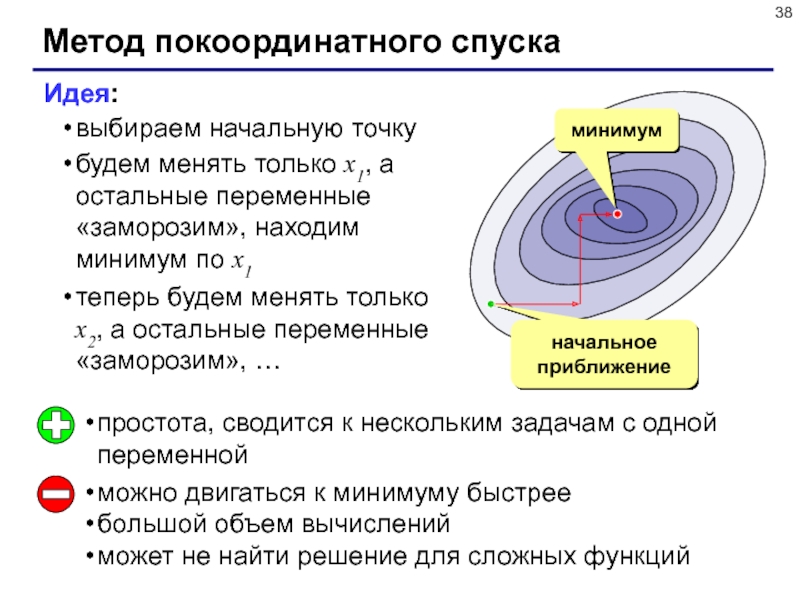
Слайд 38Метод покоординатного спуска
Идея:
выбираем начальную точку
будем менять только x1, а остальные
переменные «заморозим», находим минимум по x1
теперь будем менять только x2,
а остальные переменные «заморозим», … начальное приближение
минимум
простота, сводится к нескольким задачам с одной переменной
можно двигаться к минимуму быстрее
большой объем вычислений
может не найти решение для сложных функций
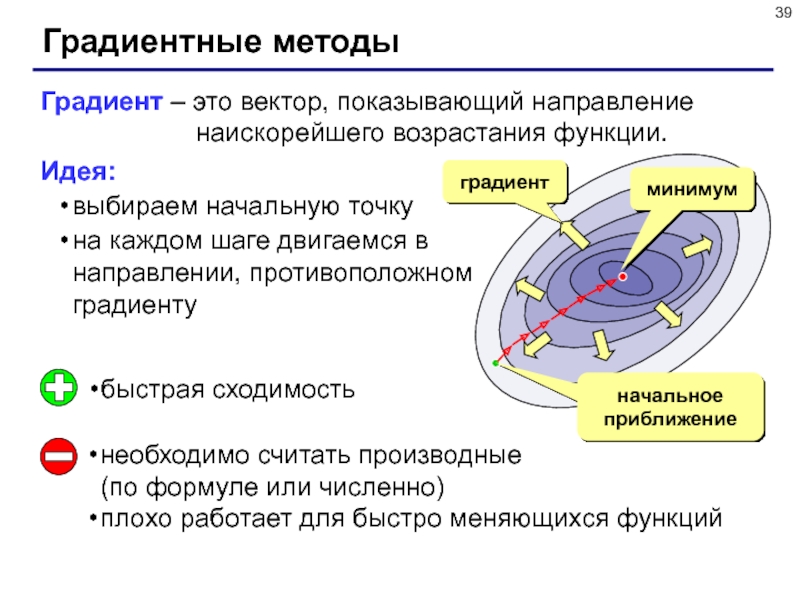
Слайд 39Градиентные методы
Градиент – это вектор, показывающий направление
наискорейшего возрастания
функции.Идея:
выбираем начальную точку
на каждом шаге двигаемся в направлении, противоположном градиенту
минимум
начальное приближение
быстрая сходимость
необходимо считать производные
(по формуле или численно)
плохо работает для быстро меняющихся функций
градиент
Слайд 40Метод случайного поиска
Идея:
выбираем начальную точку
пробуем сделать шаг в случайном направлении
если
значение функции уменьшилось, шаг удачный (запоминается)
минимум
начальное приближение
простота реализации
не требует вычисления
производныхмного вариантов с самообучением
хорошо работает для функций с многими локальными минимумами
очень большой объем вычислений
