Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цифровая обработка сигналов
Содержание
- 1. Цифровая обработка сигналов
- 2. Лекция 1Основные понятия и определения
- 3. Сигнал S(t) обычно является
- 4. Например, эквивалентная схема дифференцирующего аналогового устройства имеет
- 5. Слайд 5
- 6. В другом примере показана эквивалентная схема
- 7. Слайд 7
- 8. Наряду с аналоговыми методами,
- 9. Поэтому цифровая обработка сигнала включает
- 10. Значительным событием в развитии ЦОС
- 11. Следующим шагом в развитии ЦОС
- 12. Классификация сигналов Сигнал (от лат.
- 13. Исходный физический сигнал, например
- 14. Слайд 14
- 15. На втором графике показан дискретный сигнал (discrete
- 16. Величина, обратная периоду дискретизации, называется частотой дискретизации
- 17. Значения цифрового сигнала приведены в таблице
- 18. В зависимости от того, известен
- 19. Следующий класс сигналов –
- 20. Величина обратная периоду сигнала называется
- 21. Следующий класс – сигналы
- 22. Сигналы бесконечной длительности или нефинитные
- 23. Очень важную роль в
- 24. К тестовым сигналам относится
- 25. Иногда для образного представления
- 26. К тестовым сигналам относится также сигнал равный
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ (ЦОС)
Digital Signal Processing (DSP)
Лектор:
Корнеева Мария Викторовна
Кафедра Телекоммуникационные
системы (ТКС)
Слайд 2Лекция 1
Основные понятия и определения
Основной задачей телекоммуникационных
систем является передача сообщений на расстояние. В процессе передачи сообщений
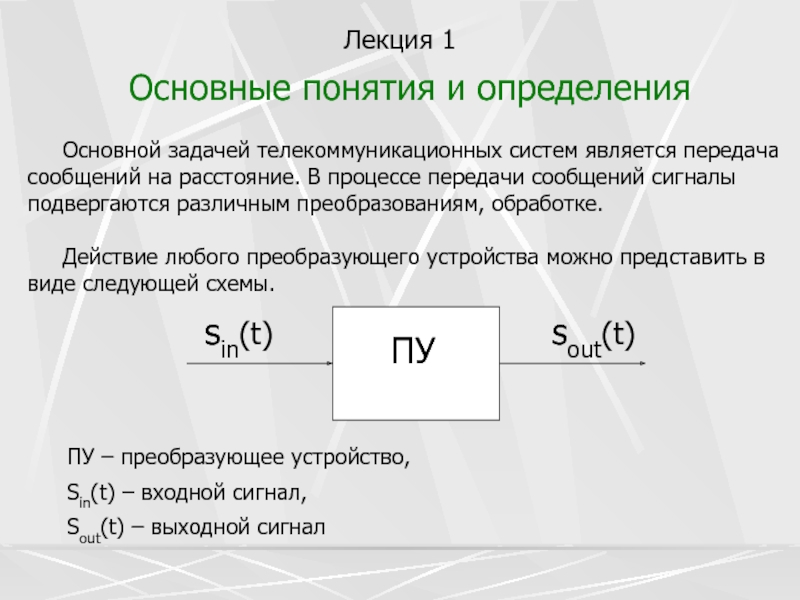
сигналы подвергаются различным преобразованиям, обработке.Действие любого преобразующего устройства можно представить в виде следующей схемы.
ПУ – преобразующее устройство,
Sin(t) – входной сигнал,
Sout(t) – выходной сигнал
Слайд 3 Сигнал S(t) обычно является напряжением, реже током.
В дальнейшем, говоря о физической природе сигнала, будем считать, что
сигнал представляет собой зависимость напряжения от времени. До недавнего времени обработка сигналов, как правило, выполнялась при помощи аналоговых устройств. Аналоговое устройство – это некоторое электронное устройство, где преобразование сигнала происходит в результате физических процессов протекающих в этом устройстве.
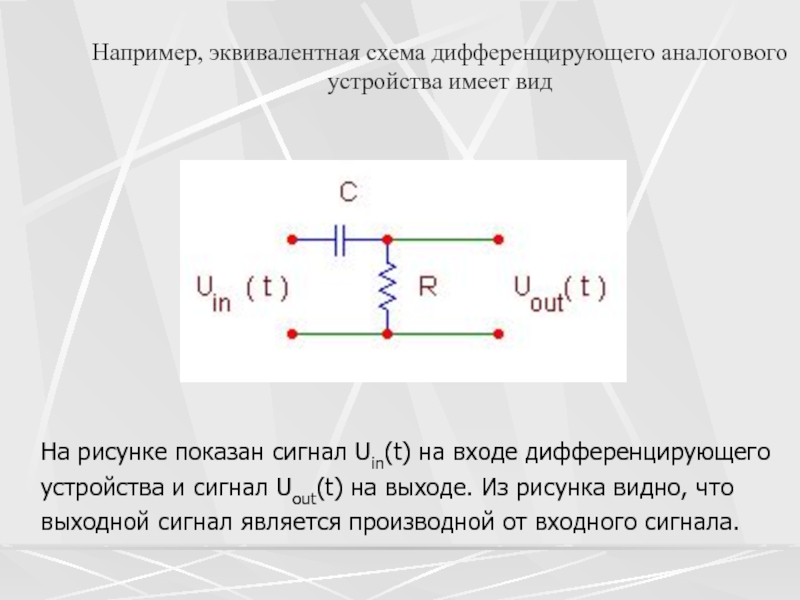
Слайд 4Например, эквивалентная схема дифференцирующего аналогового устройства имеет вид
На рисунке показан
сигнал Uin(t) на входе дифференцирующего устройства и сигнал Uout(t) на
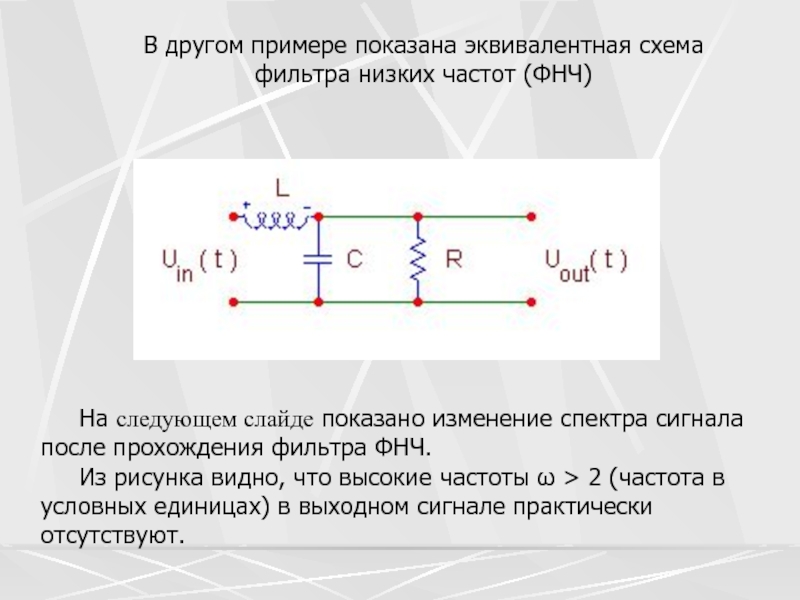
выходе. Из рисунка видно, что выходной сигнал является производной от входного сигнала.Слайд 6 В другом примере показана эквивалентная схема
фильтра низких
частот (ФНЧ)
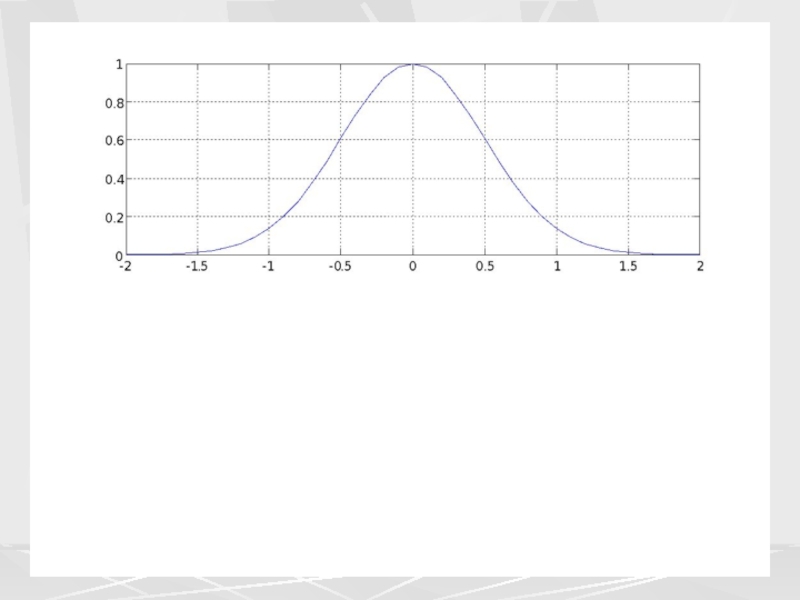
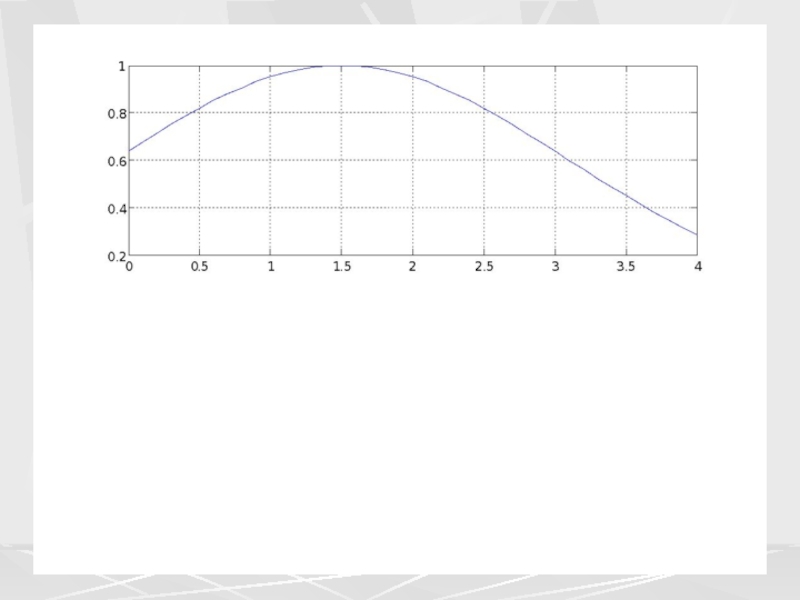
На следующем слайде показано изменение
спектра сигнала после прохождения фильтра ФНЧ. Из рисунка видно, что высокие частоты ω > 2 (частота в условных единицах) в выходном сигнале практически отсутствуют.
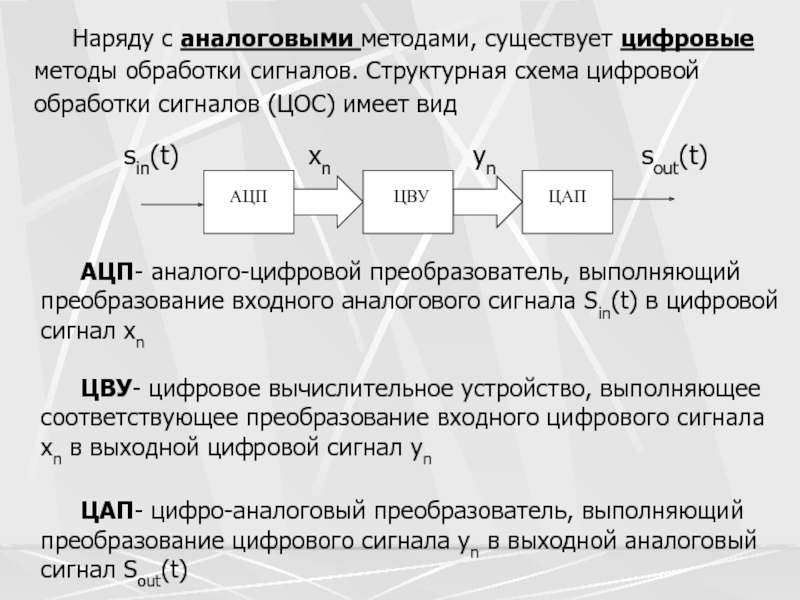
Слайд 8 Наряду с аналоговыми методами, существует цифровые методы
обработки сигналов. Структурная схема цифровой обработки сигналов (ЦОС) имеет вид
АЦП-
аналого-цифровой преобразователь, выполняющий преобразование входного аналогового сигнала Sin(t) в цифровой сигнал xn ЦВУ- цифровое вычислительное устройство, выполняющее соответствующее преобразование входного цифрового сигнала xn в выходной цифровой сигнал yn
ЦАП- цифро-аналоговый преобразователь, выполняющий преобразование цифрового сигнала yn в выходной аналоговый сигнал Sout(t)
Слайд 9 Поэтому цифровая обработка сигнала включает в себя три
основных этапа обработки.
Во-первых, это преобразование аналогового сигнала в
цифровой
сигнал. Во-вторых, обратное преобразование, т.е. восстановление аналогового сигнала из цифрового сигнала.
В-третьих, преобразование входного цифрового сигнала в выходной цифровой сигнал по определенным алгоритмам.
В зависимости от выбора алгоритмов обработки сигналов устройства ЦОС могут иметь самый разнообразный характер.
Можно, например, создавать фильтры, анализаторы спектра, нелинейные преобразователи спектра и многое другое.
Слайд 10 Значительным событием в развитии ЦОС было открытие в
1965 г. эффективных алгоритмов для вычислений преобразований Фурье. Этот класс
алгоритмов стал известен как быстрое преобразование Фурье (БПФ). Значимость этого открытия состоит в следующем. Составной частью ЦОС является спектральный анализ сигналов.
В спектральном анализе основным математическим аппаратом является преобразование Фурье, на вычисление которого тратилась значительная часть машинного времени. Алгоритм быстрого преобразования Фурье уменьшил время вычисления преобразования Фурье на несколько порядков. Это позволило создать очень сложные алгоритмы обработки сигналов в реальном времени.
Слайд 11 Следующим шагом в развитии ЦОС было появление специализированных
цифровых устройств обработки сигналов. В недалеком прошлом в качестве ЦВУ
(цифровое вычислительное устройство) применялась обычная ЭВМ. Теперь для этой цели используются процессоры цифровой обработки сигналов или сигнальные процессоры. Эти сигнальные процессоры обладают приспособленной для ЦОС архитектурой, например, быстрое преобразование Фурье выполняется на аппаратном уровне. В настоящее время системы цифровой обработки сигналов вошли в нашу повседневную жизнь в виде CD- и DVD- проигрывателей, модемов, сотовых телефонов и многого другого. В некоторых прикладных областях цифровая обработка сигналов стала вытеснять «традиционную» аналоговую обработку сигналов. В значительной мере это произошло в аудиотехнике, интенсивно идет процесс перехода телевизионного вещания на цифровую основу.
Слайд 12Классификация сигналов
Сигнал (от лат. “signum”) - некоторый
процесс изменения во времени физического состояния какого-либо объекта (напряжение), служащий
для отображения,регистрации и передачи информации. Сигнал может быть определен как функция s(t), переносящая информацию о состоянии или поведении физической системы. Математически сигналы представляются в виде функций одной или более независимых переменных.
Классификация сигналов по способу обработки
Сигналы разделяются на аналоговые, дискретные и цифровые
Слайд 13
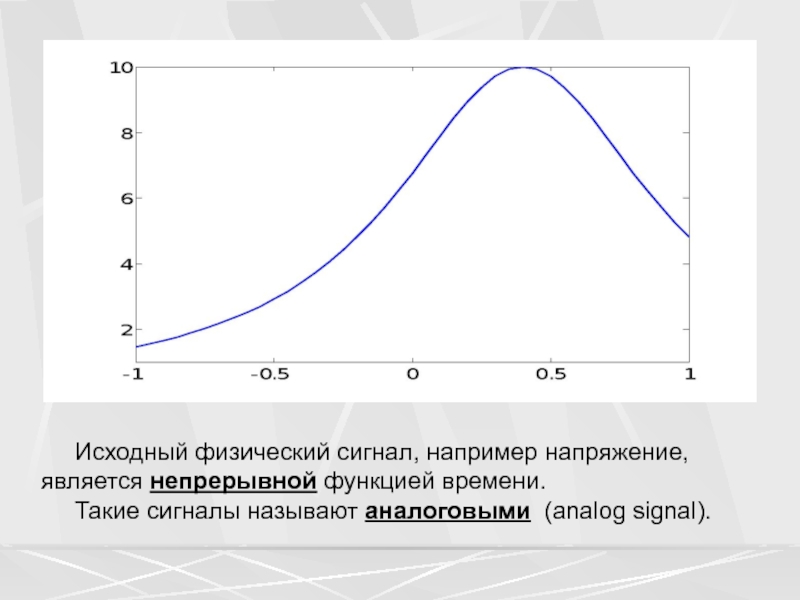
Исходный физический сигнал, например напряжение, является непрерывной
функцией времени.
Такие сигналы называют аналоговыми (analog
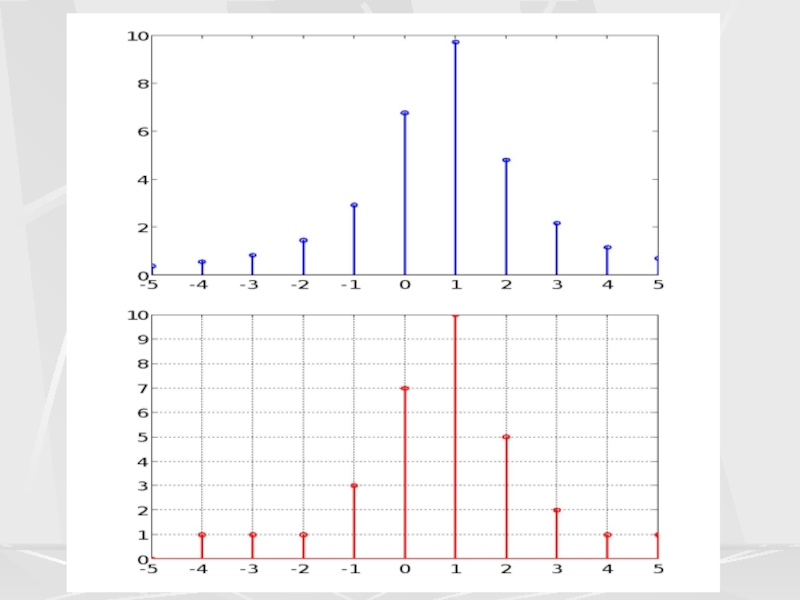
signal). Слайд 15На втором графике показан дискретный сигнал (discrete signal), полученный из
аналогового сигнала с помощью дискретизации (sampling). Дискретный сигнал это ряд
значений аналогового сигнала,в дискретные моменты времени.Числа , составляющие дискретный сигнал, называются отсчетами сигнала (samples). Обычно, отсчеты берут через равные промежутки времени , называемые периодом дискретизации (или интервалом, шагом дискретизации – sample time). В нашем примере период дискретизации выбран
Значения дискретного сигнала приведены в таблице
Слайд 16Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency).
В дальнейшем мы будем пользоваться частотой Найквиста (Nyquist frequency),
которая связана с частотой дискретизации соотношением. При обработке сигнала в вычислительных устройствах его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов (например, 16 - разрядные, 32 - разрядные). Поэтому значения дискретного сигнала округляются. Процесс такого округления называется квантованием по уровню (quantization). Дискретный сигнал, квантованный по уровню, называется цифровым сигналом (digital signal). Пример цифрового сигнала показан на третьем графике. Здесь, для примера, в качестве уровней квантования взяты целые числа.
Слайд 17Значения цифрового сигнала приведены в таблице
Возникающие при
округлении ошибки называют ошибками квантования или шумами квантования (quantization error,
quantization noise).Слайд 18 В зависимости от того, известен ли нам сигнал
точно, различают детерминированные и случайные сигналы. Детерминированный сигнал полностью известен
– его значения в любой момент времени можно определить точно. Случайный же сигнал в любой моментвремени представляет собой случайную величину, которая принимает конкретные значения с некоторой вероятностью.
Следующий важный класс сигналов – сигналы с интегрируемым квадратом. Эти сигналы называет также сигналами с ограниченной энергией. Для таких сигналов S(t) выполняется соотношение
Этот интеграл условно называется энергией сигнала E.
Классификация сигналов по физическим свойствам
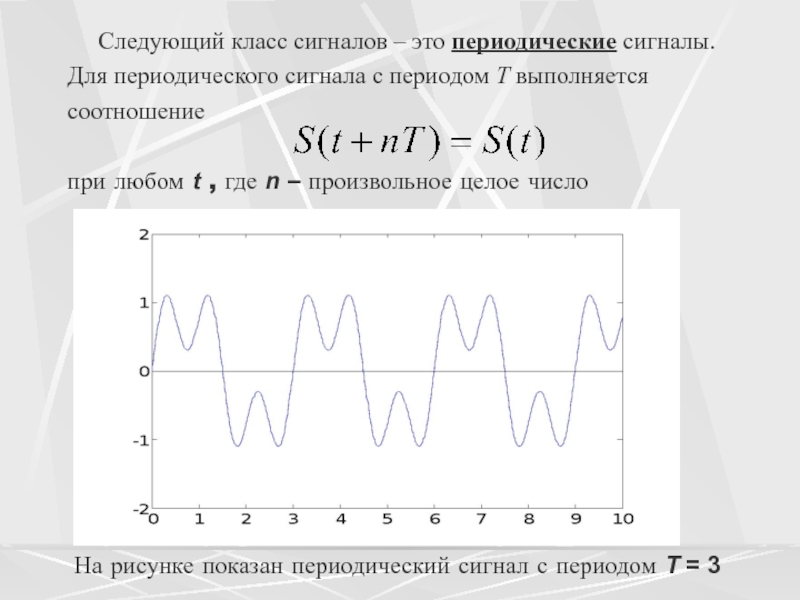
Слайд 19 Следующий класс сигналов – это периодические сигналы.
Для периодического сигнала с периодом T выполняется соотношение при любом t
, где n – произвольное целое числоНа рисунке показан периодический сигнал с периодом T = 3
Слайд 20 Величина обратная периоду сигнала называется частотой сигнала, и
измеряется в герцах (Гц).
В теории сигналов также используется круговая
частота, которая измеряется в радианах на секунду (рад/c).Любой периодический сигнал имеет бесконечную энергию, так как интеграл энергии для этих сигналов всегда расходится
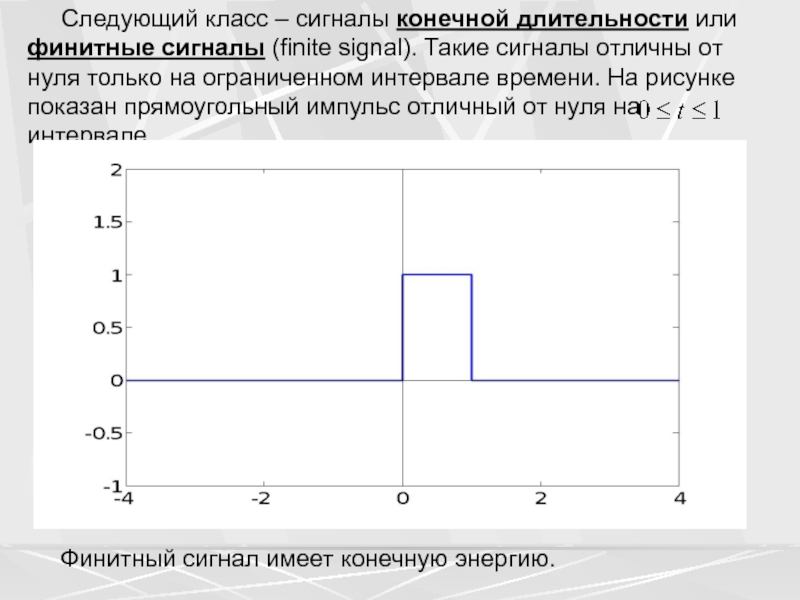
Слайд 21 Следующий класс – сигналы конечной длительности или
финитные сигналы (finite signal). Такие сигналы отличны от нуля только
на ограниченном интервале времени. На рисунке показан прямоугольный импульс отличный от нуля на интервале Финитный сигнал имеет конечную энергию.
Слайд 22 Сигналы бесконечной длительности или нефинитные сигналы
(non-finite signal)
могут быть отличны от нуля для любого момента времени. Примером
нефинитных сигналов являются любые периодические сигналы. Инфинитные сигналы могут иметь конечную энергию. Рассмотрим, например следующий инфинитный сигналГрафик этого сигнала приведен на рисунке. Легко проверить путем интегрирования, что энергия такого сигнала конечна и равна
Слайд 23
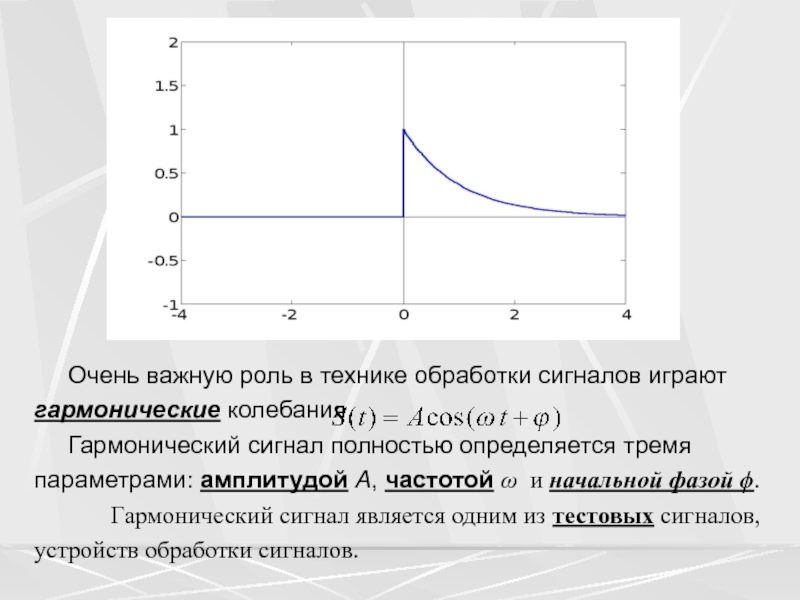
Очень важную роль в технике обработки сигналов
играют гармонические колебания
Гармонический сигнал полностью определяется
тремя параметрами: амплитудой A, частотой ω и начальной фазой ϕ. Гармонический сигнал является одним из тестовых сигналов, устройств обработки сигналов.Слайд 24 К тестовым сигналам относится также сигнал равный
дельта – функции Дирака.
где - некоторый заданный момент
времени. Дельта – функция Дирака является обобщенной функцией и определяется следующим интегральным соотношениемотсюда вытекаю свойства дельта – функции
где функция должна быть непрерывной в точке
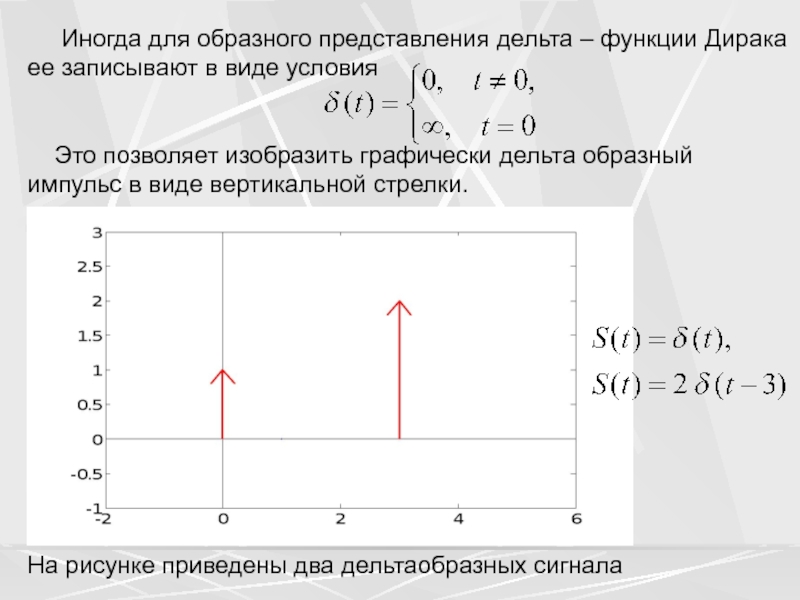
Слайд 25 Иногда для образного представления дельта – функции
Дирака ее записывают в виде условия
Это позволяет изобразить
графически дельта образный импульс в виде вертикальной стрелки.На рисунке приведены два дельтаобразных сигнала
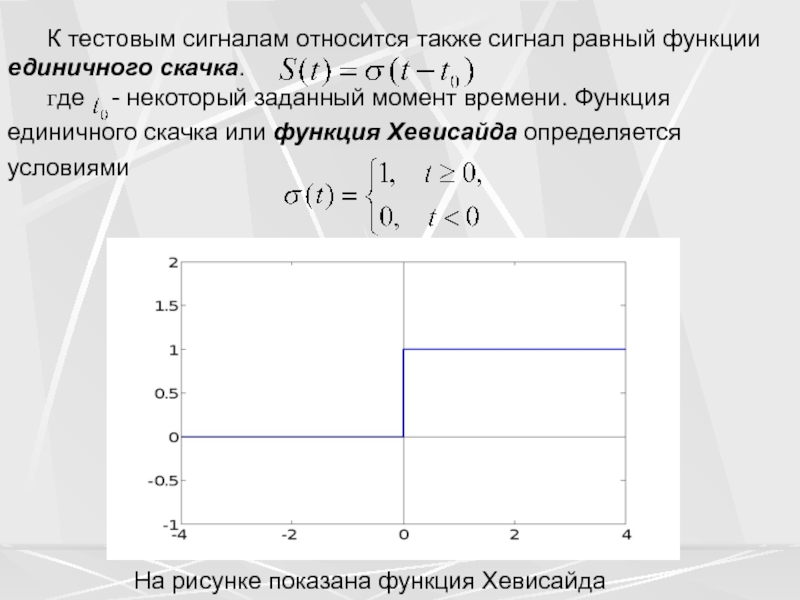
Слайд 26К тестовым сигналам относится также сигнал равный функции единичного скачка.
где - некоторый заданный момент времени. Функция единичного скачка
или функция Хевисайда определяется условиямиНа рисунке показана функция Хевисайда