Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цифровая обработка сигналов и изображений
Содержание
- 1. Цифровая обработка сигналов и изображений
- 2. Структура дисциплиныОсенний семестр 2+4 часа лекций4+4 часа лабораторных работЗачетВесенний семестр2+4 часа лекций4 часа лабораторных работЭкзамен
- 3. Минимальные требования для получения зачета в осеннем
- 4. Перечень вопросов, выносимых на зачетТипы сигналов. Связь
- 5. ЧТО ТАКОЕ СИГНАЛ?ВОЗМОЖНЫЕ ВАРИАНТЫ КЛАССИФИКАЦИИ СИГНАЛОВПРОБЛЕМА ВЫБОРКИТЕОРЕМА КОТЕЛЬНИКОВАВводная информация по курсу
- 6. Физический смысл – сигнал создается определенным процессом,
- 7. Сигналы бывают разные…Сигналы это:Различные физические величины;Различные единицы измерения;Различные масштабы переменных.
- 8. Классификация сигналовСлучайный сигнал – значение такого сигнала
- 9. Аналоговые (непрерывные)Примеры:звук в воздухе или в проводе,
- 10. Классификация колебаний КОЛЕБАНИЯ:Каузальное колебание, имеющее
- 11. Проблема выборки В процессе преобразования аналогового
- 12. Теорема Котельникова-Найквиста-Шенона Интервал дискретизации выборки
- 13. НЕОБХОДИМЫЕ МАТЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯРАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕНЕПРЕРЫВНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕРазложение в ряд Фурье
- 14. А вот и он☺Jean Baptiste Joseph Fourier
- 15. Необходимые математические представленияКомплексное представление чисел на плоскостиПредставление комплексных сопряженных чиселГрафическая иллюстрация формулы Эйлера
- 16. Необходимые математические представленияАбсолютная величина (модуль) числаАргумент числа
- 17. Ортогональные функции Множество непрерывных функций действительного переменного
- 18. Впервые в 1807 году французский математик и
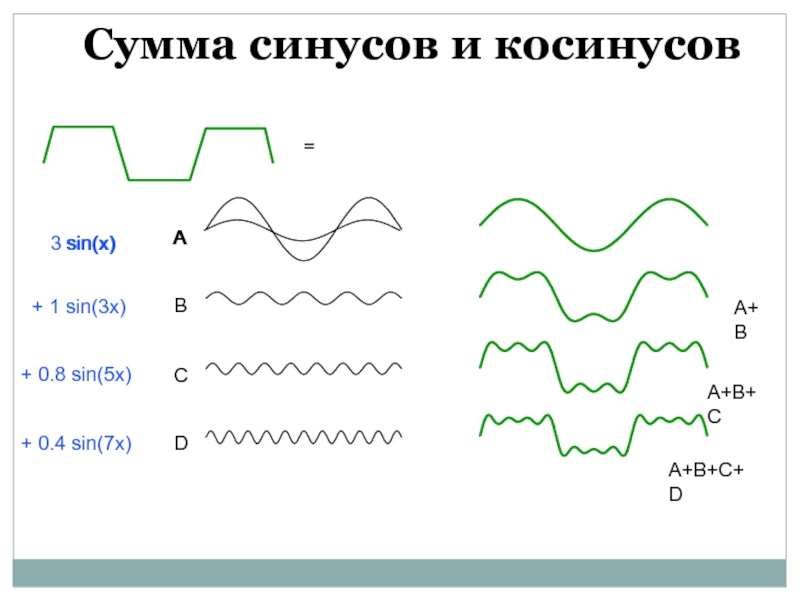
- 19. = Сумма синусов и косинусов
- 20. Прямое и обратное преобразования Фурьеx(t) – исходная
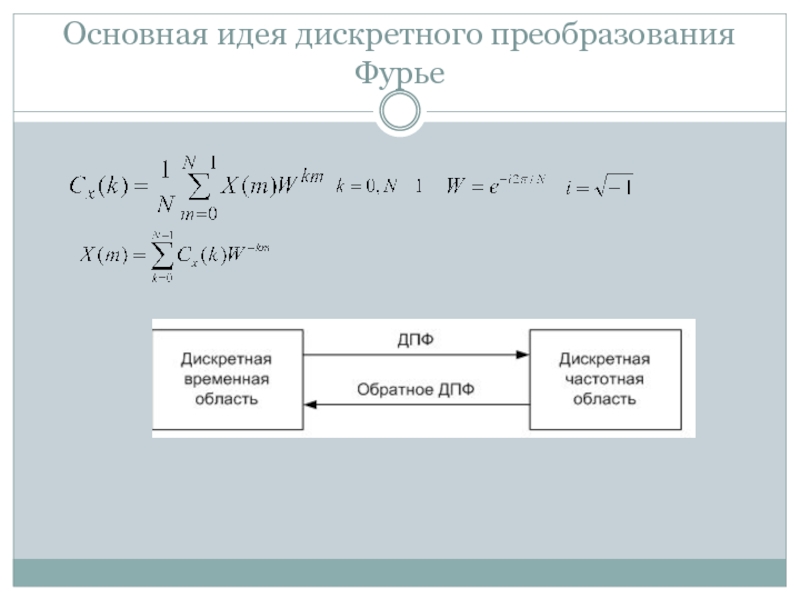
- 21. Основная идея дискретного преобразования Фурье
- 22. БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИБПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕАлгоритм быстрого преобразования Фурье
- 23. Дискретное преобразование Фурье (ДПФ)Вычислительная сложность: Каждый коэффициент
- 24. 8-точечное ДПФ (N=8)
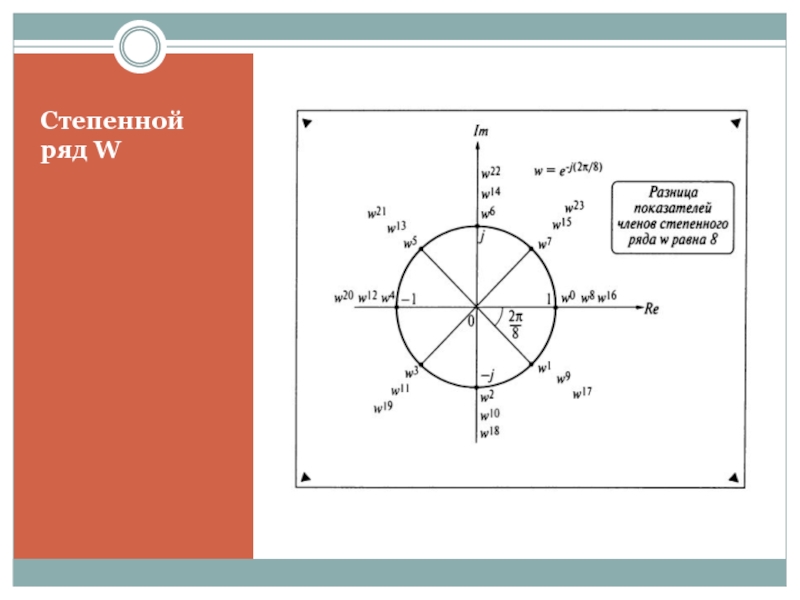
- 25. Степенной ряд W
- 26. Алгоритм БПФ с прореживанием по времениПрименяются свойства
- 27. Прореживание по времениПример 8-точечного ДПФ с прореживанием
- 28. Прореживание по времениПосле двух шагов прореживания по времениПовторять пока не останутся 2-точечные ДПФ
- 29. Алгоритм БПФ С прореживанием по времениФинальная граф-схема алгоритма для N=8Вычислительная сложность:Nlog2N комплексных сложений и умножений
- 30. Вычисление «бабочки»Следующий граф определяет бабочкуМы можем реализовать
- 31. Примечание к алгоритмуОтметим последовательность входных элементовБит-реверсная индексация
- 32. Примечание к алгоритму
- 33. Алгоритм БПФ с прореживанием по частотеДПФРазделим ДПФ на две части («верхняя» и «нижняя»)ПолучимАналогично для второй половины
- 34. Алгоритм БПФ с прореживанием по частотеФинальная граф-схема алгоритма для N=8
- 35. БПФ с прореживанием по времениБПФ с прореживанием
- 36. Практическое применение
- 37. Спектральный анализОтображение спектров изображенийСпектр – это картинка,
- 38. Спектральный анализПримеры изображений и их спектровВидно, что
- 39. Спектральный анализПримеры изображений и их спектровПо спектру
- 40. Спектральный анализОтображение спектра звука: спектрограммаСпектрограмма – график
- 41. Двумерное ДПФ, пример
- 42. Двумерное ДПФ, пример
- 43. Frequency BandsPercentage of image power enclosed in
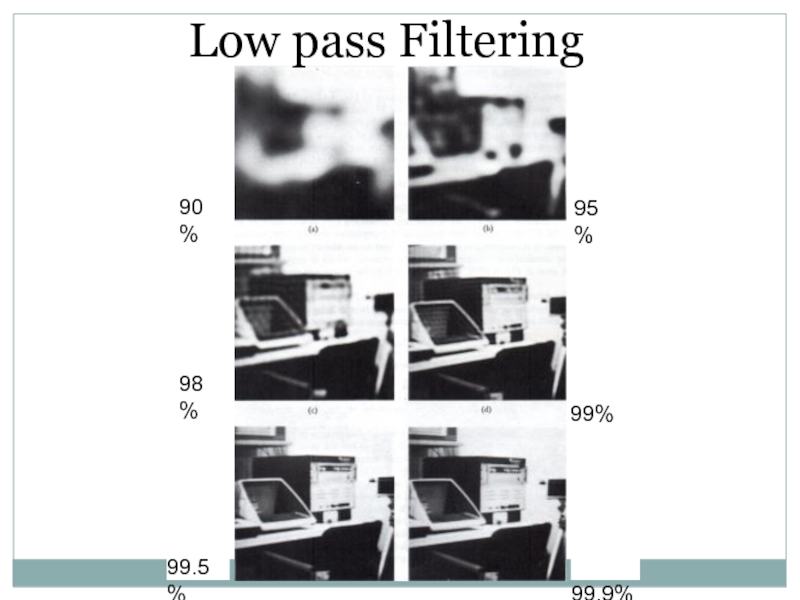
- 44. Low pass Filtering90%95%98% 99%99.5% 99.9%
- 45. Noise RemovalNoisy image
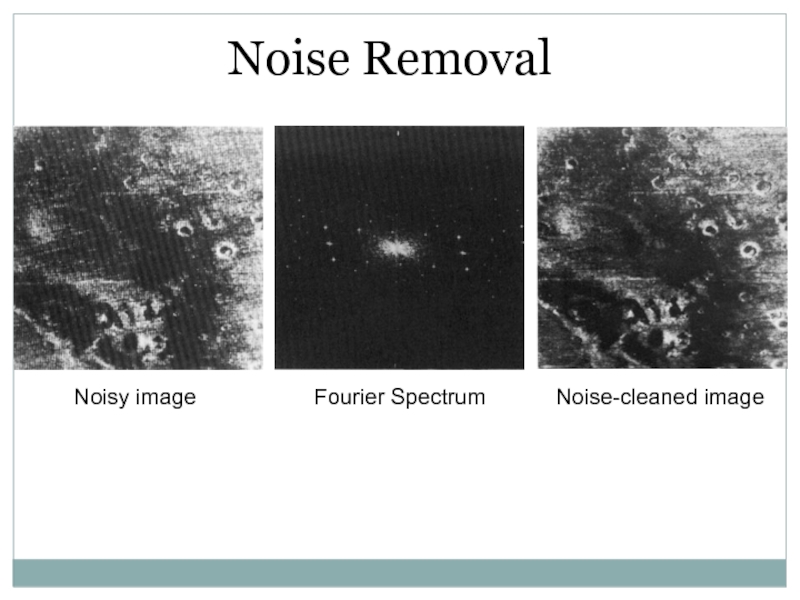
- 46. Noise RemovalNoisy imageFourier SpectrumNoise-cleaned image
- 47. High Pass FilteringOriginalHigh Pass Filtered
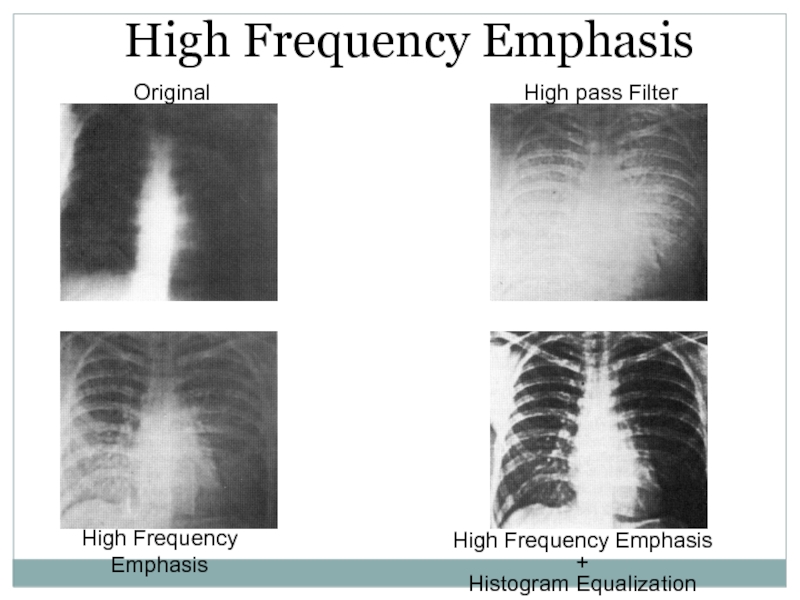
- 48. High Frequency Emphasis+OriginalHigh Pass Filtered
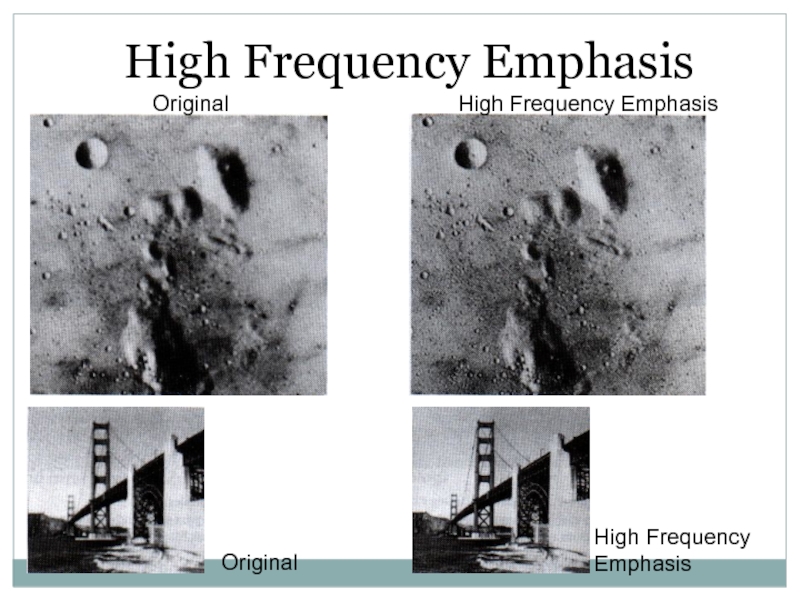
- 49. High Frequency EmphasisOriginalHigh Frequency EmphasisOriginalHigh Frequency Emphasis
- 50. OriginalHigh Frequency Emphasis
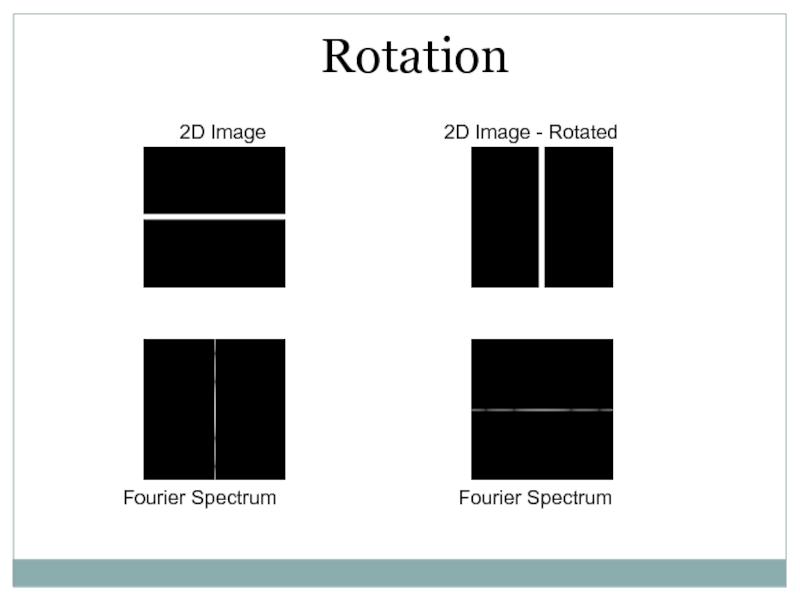
- 51. 2D ImageRotation
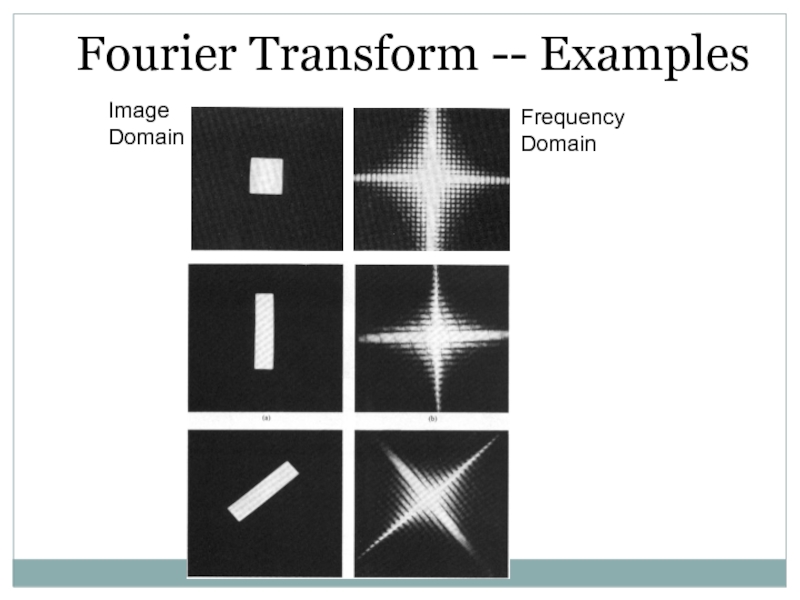
- 52. Image DomainFrequency DomainFourier Transform -- Examples
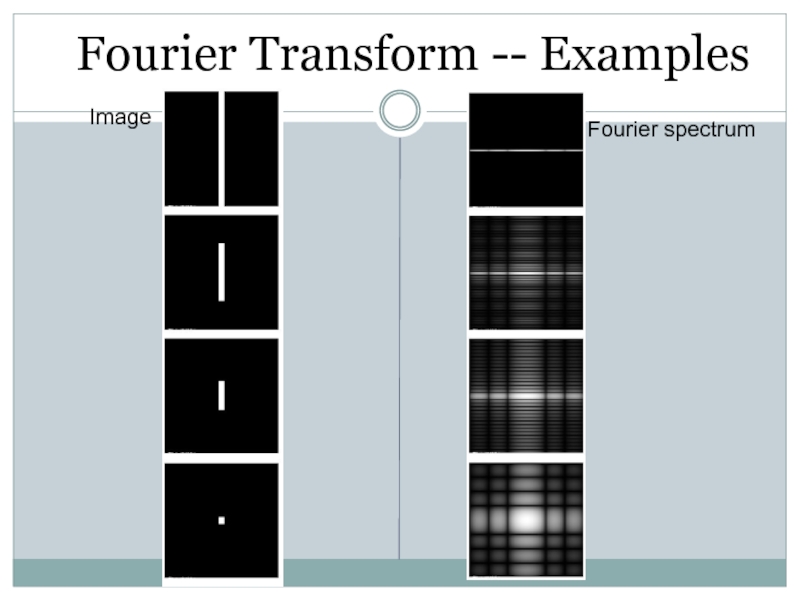
- 53. ImageFourier spectrumFourier Transform -- Examples
- 54. ЧТО ЖЕ МЫ ТАМ НАПИСАЛИ, ИСХОДЯ ИЗ ТОГО, ЧТО МЫ СЕЙЧАС ПРОСЛУШАЛИ…Контрольная работа
- 55. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЭКЗАМЕНАЦИОННАЯ СЕССИЯ
ПРЕПОДАВАТЕЛЬ
АССИСТЕНТ КАФЕДРЫ ЭВМ
ЛУКАШЕВИЧ МАРИНА МИХАЙЛОВНА
Цифровая обработка сигналов и изображений
Слайд 2Структура дисциплины
Осенний семестр
2+4 часа лекций
4+4 часа лабораторных работ
Зачет
Весенний семестр
2+4
часа лекций
Слайд 3Минимальные требования для получения зачета в осеннем семестре
Сдать и защитить
контрольную работу (КР защищается индивидуально каждым студентом).
Выполнить и защитить ДВЕ
лабораторные работы (выполнение и защита ЛР возможна в бригаде в составе двух человек).ЗАЧЕТ (два теоретических вопроса из перечня).
До зачета допускаются студенты, защитившие КР и две ЛР.
Слайд 4Перечень вопросов, выносимых на зачет
Типы сигналов. Связь между сигналами различных
типов.
Задачи анализа и синтеза сигналов.
Представление сигнала с помощью ортогональных функций.
Ряд
Фурье. Преобразование Фурье.Теорема корреляции.
Теорема свертки.
Теорема отсчетов.
Определение дискретного преобразования Фурье (ДПФ) и обратного дискретного преобразования Фурье (ОБПФ).
Свойства ДПФ (теорема линейности, теорема комплексной сопряженности, теорема сдвига, теорема сверки, теорема корреляции).
Вычислительная сложность ДПФ.
Двумерное ДПФ.
Алгоритм быстрого преобразования Фурье (БПФ) с децимацией во временной области.
Вычислительные преимущества БПФ.
Обратное быстрое преобразование Фурье.
БПФ с частотной децимацией.
Схемы вычисления свертки и корреляции на основе БПФ.
Класс несинусоидальных ортогональных функций (функции Радемахера, функции Хаара, функции Уолша).
Код Грея.
Преобразование Уолша.
Преобразование Уолша-Адамара (Адамара).
Алгоритм быстрого преобразования Уолша-Адамара.
Дискретное косинусное преобразование (ДКП). Применение ДКП: сжатие изображений (алгоритм JPEG).
Вейвлет- преобразование. Принцип неопределенности Гейзенберга.
Кратномасштабный анализ.
Дискретное вейвлет-преобразвование. Алгоритм JPEG 2000.
Слайд 5ЧТО ТАКОЕ СИГНАЛ?
ВОЗМОЖНЫЕ ВАРИАНТЫ КЛАССИФИКАЦИИ СИГНАЛОВ
ПРОБЛЕМА ВЫБОРКИ
ТЕОРЕМА КОТЕЛЬНИКОВА
Вводная информация
по курсу
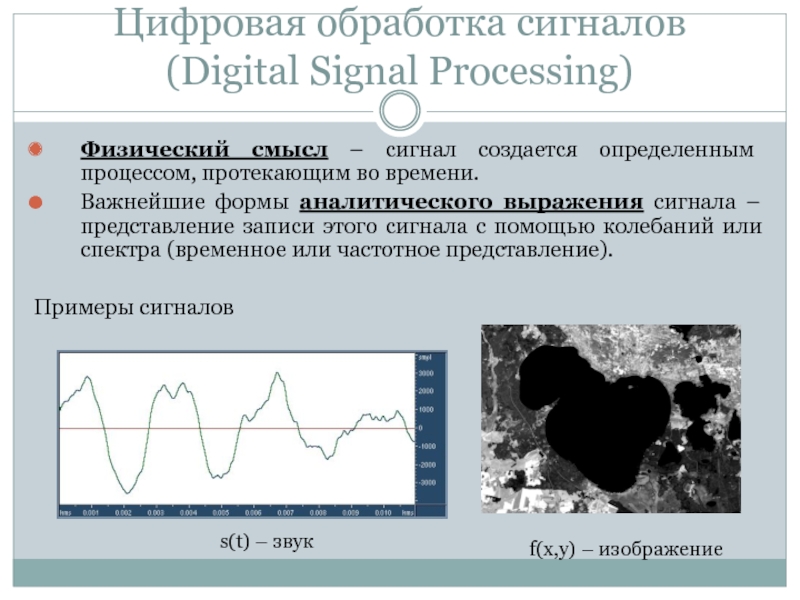
Слайд 6Физический смысл – сигнал создается определенным процессом, протекающим во времени.
Важнейшие
формы аналитического выражения сигнала – представление записи этого сигнала с
помощью колебаний или спектра (временное или частотное представление).Примеры сигналов
Цифровая обработка сигналов
(Digital Signal Processing)
s(t) – звук
f(x,y) – изображение
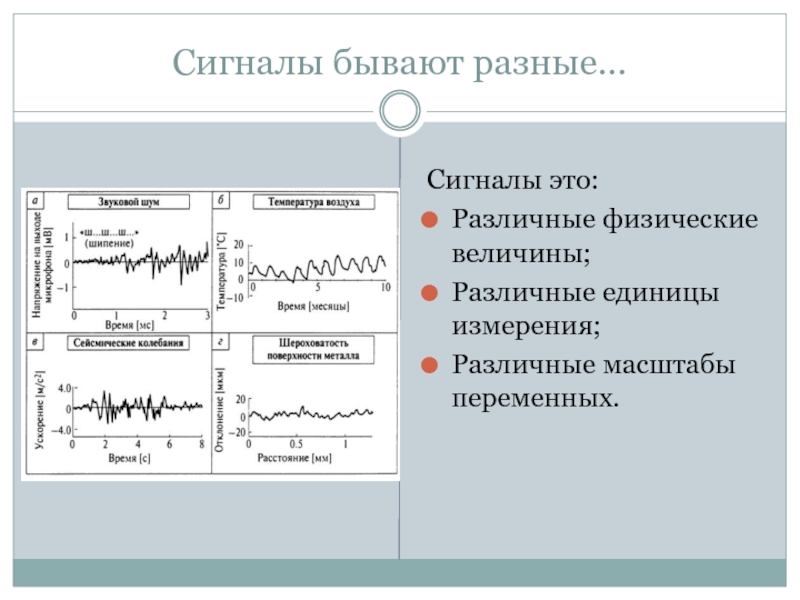
Слайд 7Сигналы бывают разные…
Сигналы это:
Различные физические величины;
Различные единицы измерения;
Различные масштабы переменных.
Слайд 8Классификация сигналов
Случайный сигнал – значение такого сигнала в любой момент
времени является случайной величиной.
Детерминированный сигнал – величину такого сигнала можно
предсказать в любой момент времени (в любой точке).Слайд 9Аналоговые (непрерывные)
Примеры:
звук в воздухе или в проводе, идущем от микрофона
изображение
(до ввода в компьютер)
запись показаний датчика
Цифровые (дискретные)
Примеры:
звук в компьютере (одномерный
массив чисел)изображение в компьютере (двумерный массив чисел)
запись показаний датчика в компьютере (одномерный массив)
Классификация сигналов
Слайд 10Классификация колебаний
КОЛЕБАНИЯ:
Каузальное
колебание, имеющее начало во
времени, которое можно рассматривать как причинное.
Периодическое
колебание,
которое задается на интервале и любое значение повторяется через интервалы времени, равные Т (период):Финитное
колебание, локализованное во времени, т.е. колебание равное нулю вне некоторого ограниченного интервала времени
Непрерывное
колебание, которое рассматривается в каждой точке оси времени, т.е. такое колебание задано на несчетном временном интервале
Дискретное
колебание рассматривается только в фиксированный момент времени, т.е. заданное на счетном множестве временных точек
Слайд 11Проблема выборки
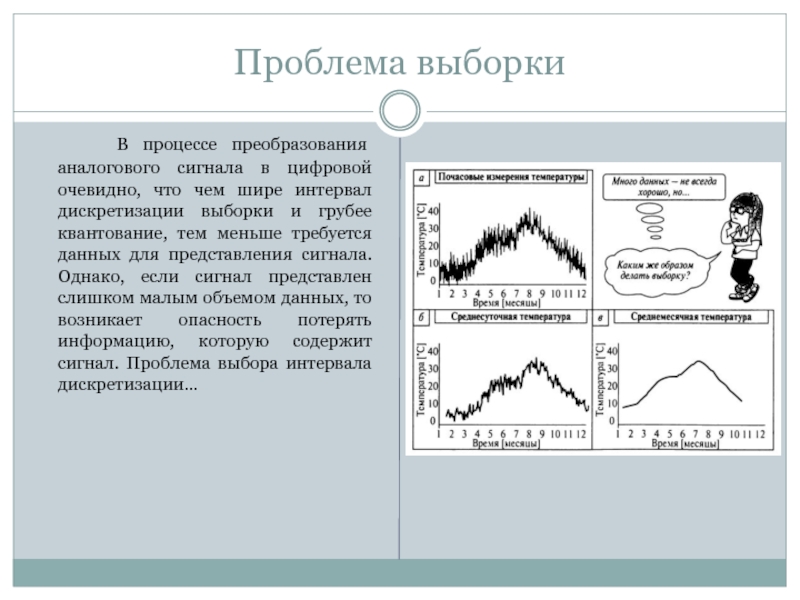
В процессе преобразования аналогового сигнала в цифровой
очевидно, что чем шире интервал дискретизации выборки и грубее квантование,
тем меньше требуется данных для представления сигнала. Однако, если сигнал представлен слишком малым объемом данных, то возникает опасность потерять информацию, которую содержит сигнал. Проблема выбора интервала дискретизации…Слайд 12Теорема Котельникова-Найквиста-Шенона
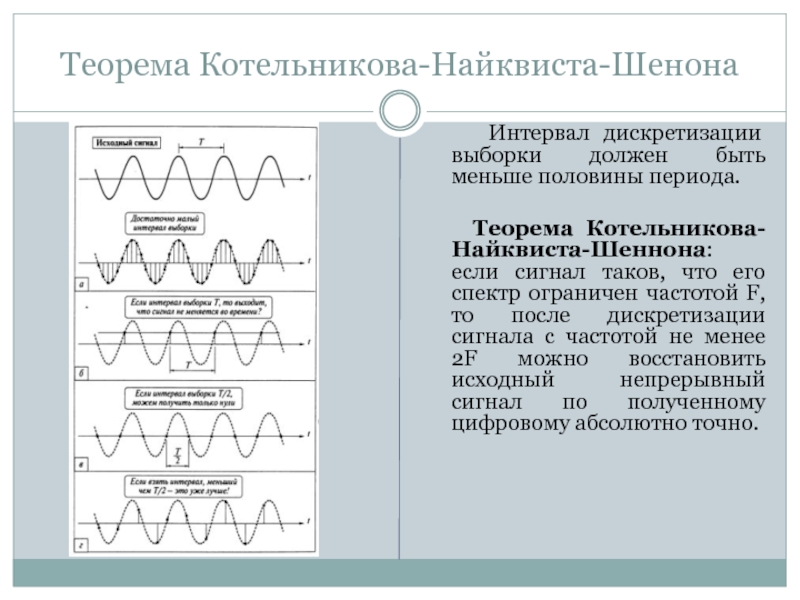
Интервал дискретизации выборки должен быть меньше
половины периода.
Теорема Котельникова-Найквиста-Шеннона: если сигнал таков, что его
спектр ограничен частотой F, то после дискретизации сигнала с частотой не менее 2F можно восстановить исходный непрерывный сигнал по полученному цифровому абсолютно точно.Слайд 13НЕОБХОДИМЫЕ МАТЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ
РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ
НЕПРЕРЫВНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ
ФУРЬЕ
Разложение в ряд Фурье
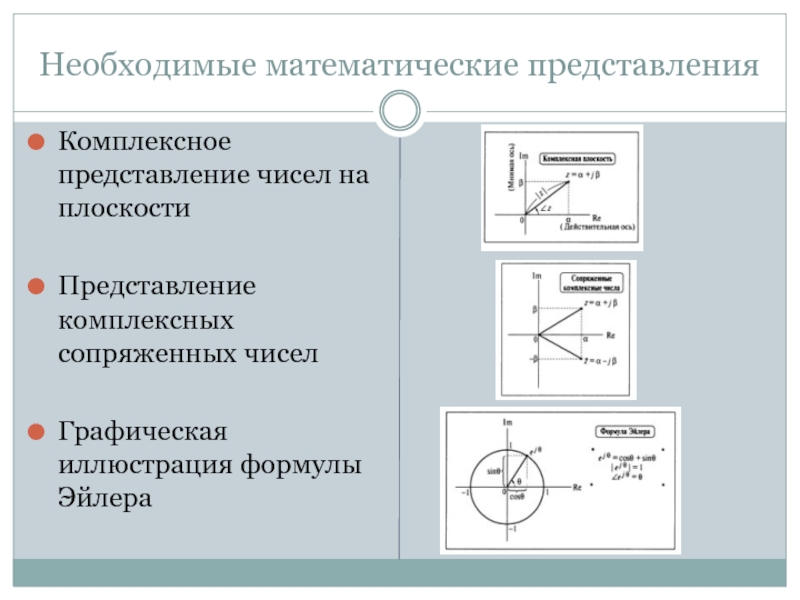
Слайд 15Необходимые математические представления
Комплексное представление чисел на плоскости
Представление комплексных сопряженных чисел
Графическая
иллюстрация формулы Эйлера
Слайд 17Ортогональные функции
Множество непрерывных функций действительного переменного
называется ортогональным
на интервале ,
еслиПри множество {Un(t)} называется ортонормированным.
Слайд 18 Впервые в 1807 году французский математик и физик Жан Батист
Жозеф Фурье показал, что любую произвольную функцию
можно представить в виде бесконечной суммы синусных и косинусных членов:где (рад/с) – основная угловая частота, которая связана с периодом T функции соотношением . Частоты называют гармониками, так как они кратны основной частоте . В данном случае речь идет о системе ортогональных функций вида
Разложение функции в ряд Фурье
Слайд 20Прямое и обратное преобразования Фурье
x(t) – исходная функция времени
Прямое преобразование
Фурье
(отображение исходной функции времени в спектральную область)
Обратное преобразование Фурье
(восстановление
функции по её спектру)
Слайд 22БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ
БПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ
Алгоритм быстрого
преобразования Фурье
Слайд 23Дискретное преобразование Фурье (ДПФ)
Вычислительная сложность:
Каждый коэффициент ДПФ требует:
N комплексных
умножений
N-1 комплексных сложений
Все N коэффициентов ДПФ требуют:
N2 комплексных умножений
N(N-1) комплексных
сложенийБолее быстрые методы основаны на свойствах симметрии и периодичности
Симметрия
Периодичность
Слайд 26Алгоритм БПФ с прореживанием по времени
Применяются свойства симметрии и периодичности
Рассматривается
для случаев, когда
Разделим x[n] на две последовательности длиной N/2
Четные
элементы в первой последовательностиНечетные элементы во второй последовательности
Пусть n=2r для четных и n=2r+1 для нечетных элементов
G[k] и H[k] - N/2-точечные ДПФ для каждой последовательности
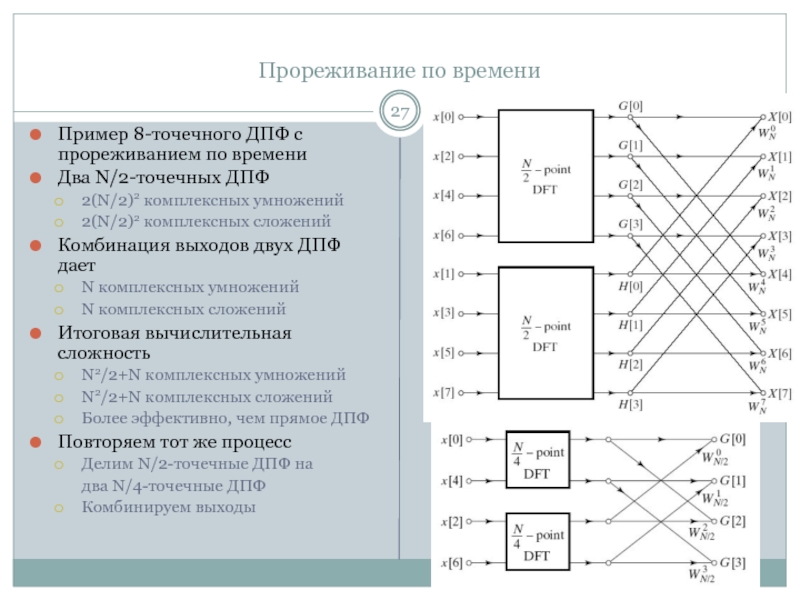
Слайд 27Прореживание по времени
Пример 8-точечного ДПФ с прореживанием по времени
Два N/2-точечных
ДПФ
2(N/2)2 комплексных умножений
2(N/2)2 комплексных сложений
Комбинация выходов двух ДПФ дает
N комплексных
умноженийN комплексных сложений
Итоговая вычислительная сложность
N2/2+N комплексных умножений
N2/2+N комплексных сложений
Более эффективно, чем прямое ДПФ
Повторяем тот же процесс
Делим N/2-точечные ДПФ на
два N/4-точечные ДПФ
Комбинируем выходы
Слайд 28Прореживание по времени
После двух шагов прореживания по времени
Повторять пока не
останутся 2-точечные ДПФ
Слайд 29Алгоритм БПФ С прореживанием по времени
Финальная граф-схема алгоритма для N=8
Вычислительная
сложность:
Nlog2N комплексных сложений и умножений
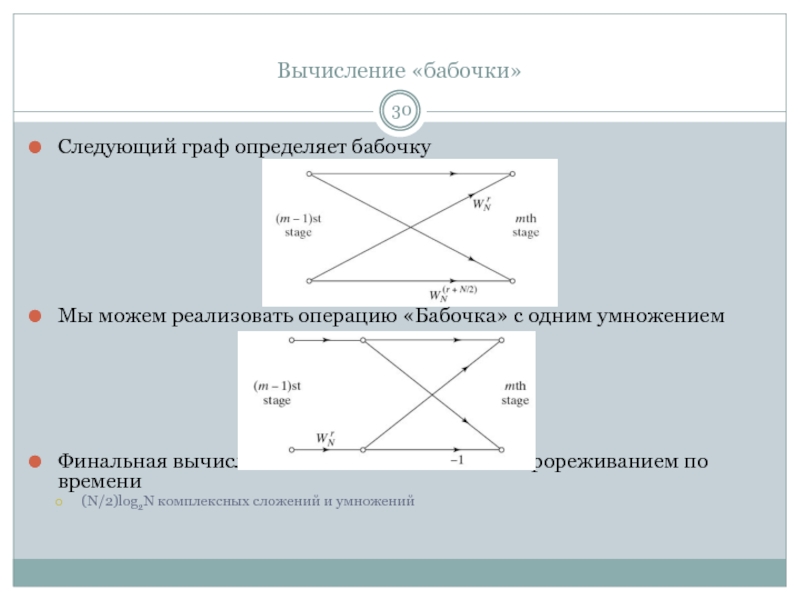
Слайд 30Вычисление «бабочки»
Следующий граф определяет бабочку
Мы можем реализовать операцию «Бабочка» с
одним умножением
Финальная вычислительная сложность БПФ с прореживанием по времени
(N/2)log2N комплексных
сложений и умноженийСлайд 33Алгоритм БПФ с прореживанием по частоте
ДПФ
Разделим ДПФ на две части
(«верхняя» и «нижняя»)
Получим
Аналогично для второй половины
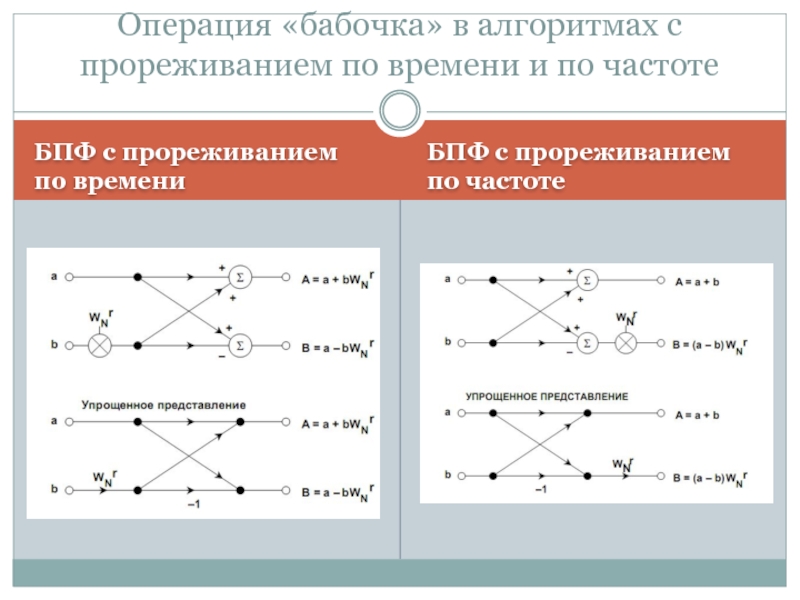
Слайд 35БПФ с прореживанием по времени
БПФ с прореживанием по частоте
Операция «бабочка»
в алгоритмах с прореживанием по времени и по частоте
Слайд 37
Спектральный анализ
Отображение спектров изображений
Спектр – это картинка, показывающая зависимость амплитуды
от частоты и от направления синусоиды.
Амплитуды отображаются в виде яркостей.
Нулевая
частота – в центре спектра, низкие частоты вокруг центра, высокие – дальше от центра.Спектр обычно продублирован отражением от нулевой частоты.
В реальных изображениях чаще всего гораздо большие амплитуды имеют низкие частоты (и постоянная составляющая). Поэтому постоянную составляющую иногда удаляют, или применяют логарифмический масштаб отображения амплитуд, чтобы пара самый мощных гармоник не скрыла остальные, менее мощные, но тоже существенные гармоники.
Слайд 38
Спектральный анализ
Примеры изображений и их спектров
Видно, что спектр одной синусоиды
– это точка
(не забываем про симметричное отражение спектра)
Две синусоиды –
две точкиСлайд 39
Спектральный анализ
Примеры изображений и их спектров
По спектру прослеживаются преобладающие направления
в исходной картинке
Много высоких частот в спектре – много мелких
деталей в исходном изображенииСлайд 40
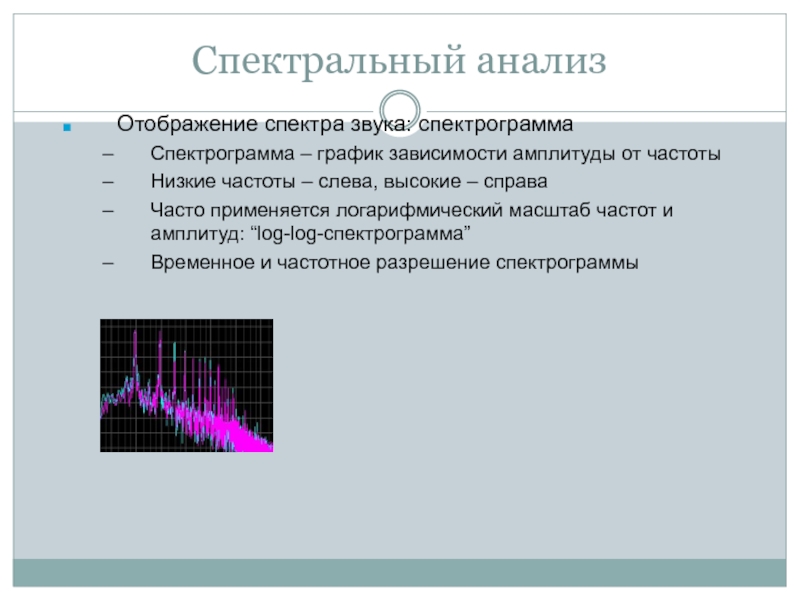
Спектральный анализ
Отображение спектра звука: спектрограмма
Спектрограмма – график зависимости амплитуды от
частоты
Низкие частоты – слева, высокие – справа
Часто применяется логарифмический масштаб
частот и амплитуд: “log-log-спектрограмма”Временное и частотное разрешение спектрограммы
Слайд 43Frequency Bands
Percentage of image power enclosed in circles (small to
large) :
90%, 95%, 98%, 99%, 99.5%,
99.9%Image
Fourier Spectrum

















![Цифровая обработка сигналов и изображений Алгоритм БПФ с прореживанием по времениПрименяются свойства симметрии и периодичностиРассматривается для Алгоритм БПФ с прореживанием по времениПрименяются свойства симметрии и периодичностиРассматривается для случаев, когда Разделим x[n] на две](/img/thumbs/78a154a8bb84f02fa04e1fa229a470ea-800x.jpg)