Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Циркуляция
Содержание
- 1. Циркуляция
- 2. Уравнения гидро-, термодинамики атмосферы – база всех
- 3. Из математики: векторное произведениеВектор C – векторное
- 4. Из механики: момент силы (τ), момент импульса
- 5. Справка: Момент импульса Земли:Вектор момента направлен по
- 6. Полезность момента при описании вращательного движенияВнутреннее вращение
- 7. Циклоны вращаются в одну сторону с Землей
- 8. Вращение Земли – это наилучшая демонстрация закона
- 9. Это значит:Эффект внутреннего циклонов и антициклонов в
- 10. Справка: нормальная и касательная скоростиСкорость V в
- 11. Справка: криволинейный интегралОпределениеСпособы вычисления: формула ГринаНезависимость
- 12. Если проинтегрировать по контуру нормальную составляющую, то
- 13. Если проинтегрировать по контуру касательную составляющую, то получим циркуляцию по контуру
- 14. циркуляция позволяет оценить угловой момент для частиц
- 15. Смысл: циркуляция показывает в какую сторону жидкость
- 16. Свойства1. Сумма циркуляций по контурам, у которых
- 17. Справка: док-во теоремы Томпсона
- 18. Важно запомнить!Если вертикальные токи растягивают объем по
- 19. Но почему возникает циркуляция ?
- 20. Важнейшей для нас фактор изменения циркуляции описывает
- 21. Справка: доказательство теоремы Бьеркнеса Если бы атмосфера
- 22. Помнить: что бароклинность – причина циркуляции ?Бароклинность
- 23. Важное следствие:В баротропной жидкости (ρ=F(p)) циркуляция по
- 24. Применение теоремы Бьеркнеса: направление и знак циркуляцииВ
- 25. Определение знака циркуляции по выделенному контуру изобаро-изострерических
- 26. Экзаменационный вопрос: вывести формулу для определения циркуляции по контуру, состоящему из двух изобар и двух изотерм
- 27. Пример – образование бризов
- 28. Экзаменационный вопрос: вывести формулу для определения циркуляции по контуру, состоящему из двух изобар и двух вертикалей
- 29. Еще примеры бароклинных зон в атмосфере Конвективная ячейкаФронтальная зонаГорно-долинные области
- 30. Экзаменационный вопрос: Оценить ускорение циркуляции в ячейке
- 31. Изменение циркуляция под влиянием трения За счет
- 32. Оценить влияние трения на скорость установившейся циркуляции
- 33. Экзам.вопрос: влияние вращения Земли на изменение циркуляции.
- 34. Экзам.вопрос: влияние вращения Земли на изменение циркуляции.
- 35. Экзам.вопрос: влияние вращения Земли на изменение циркуляции.
- 36. Экзам.вопрос: влияние вращения Земли на изменение циркуляции.
- 37. Пример: влияние вращения Земли на изменение циркуляции
- 38. Примеры влияния изменения площадиВ пассатах площадь
- 39. Задачи-минутки: решил, значит все понялЦиклоническая и
- 40. Не по теме – задачи из
- 41. Не по теме – задачи из
- 42. Не по теме – задачи из
- 43. Не по теме – задачи из
- 44. Конец
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Уравнения гидро-, термодинамики атмосферы – база всех исследований
Выражают законы
Сохранения импульса
Сохранения
массы
Сохранения полной энергии
Сохранения массы влаги
Векторная форма эффективна:
Запись короче
Запись не зависит
от системы координатПравила операций изучены
На их основе изучают свойства движений. Сегодня рассмотрим вращение
Слайд 3Из математики: векторное произведение
Вектор C – векторное произведение
На рисунке (правая
тройка) оно положительно
Направление движения – от A к B (против
часовой стрелки) также должно быть положительнымИменно поэтому вращение против часовой стрелки считается положительным (Zn), а против - отрицательным (Az)
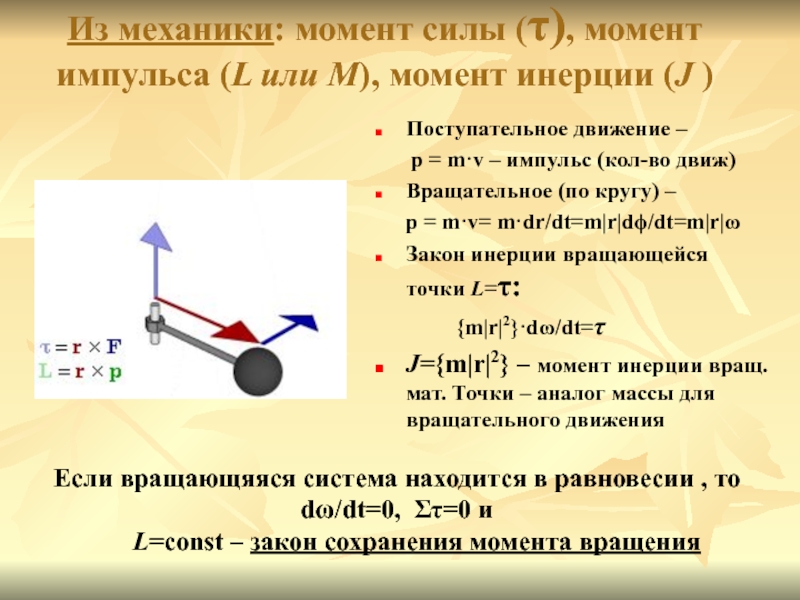
Слайд 4Из механики: момент силы (τ), момент импульса (L или M),
момент инерции (J )
Поступательное движение –
p = m·v –
импульс (кол-во движ)Вращательное (по кругу) –
p = m·v= m·dr/dt=m|r|dϕ/dt=m|r|ω
Закон инерции вращающейся точки L=τ:
{m|r|2}·dω/dt=τ
J={m|r|2} – момент инерции вращ. мат. Точки – аналог массы для вращательного движения
Если вращающяяся система находится в равновесии , то dω/dt=0, Στ=0 и
L=const – закон сохранения момента вращения
Слайд 5Справка: Момент импульса Земли:
Вектор момента направлен по оси Земли от
ЮП к СП
Фигурист (60кг, радиус 0,5 м), вращ. со скор.
1 оборот/с. создает момент импульса ≅ 100 кгм2/с. Все население Земли (10 млрд), став вращ. фигуристами не сможет сущ. изменить момент импульса Земли)Слайд 6Полезность момента при описании вращательного движения
Внутреннее вращение в изолированной системе
при сохранении общего углового момента должно изменять вращение остальных частей
системы!Пример: Если вращающееся колесо в руках повернуть осью вниз, то человек будет вращаться в противоположную сторону
Слайд 7 Циклоны вращаются в одну сторону с Землей (отнимают момент от
Земли).
Антициклоны - в другую (передают момент Земле)
Слайд 8Вращение Земли – это наилучшая демонстрация закона
сохранения момента импульса
Изо
дня в день миллионы лет вращается Земля с практически постоянной
угловой скоростью.Вектор угловой скорости (он направлен по оси от ЮП к СП) имеет и сохраняет направление, перпендикулярное плоскости орбиты.
Только постепенное удаление Луны, увеличивает радиус вращения системы З-Л и замедляет скорость вращения, сокращая сутки примерно на 1 с за 100 лет
Слайд 9Это значит:
Эффект внутреннего циклонов и антициклонов в атмосфере в целом
должен скомпенсироваться
Но этот эффект обязательно все же проявляется в изменениях
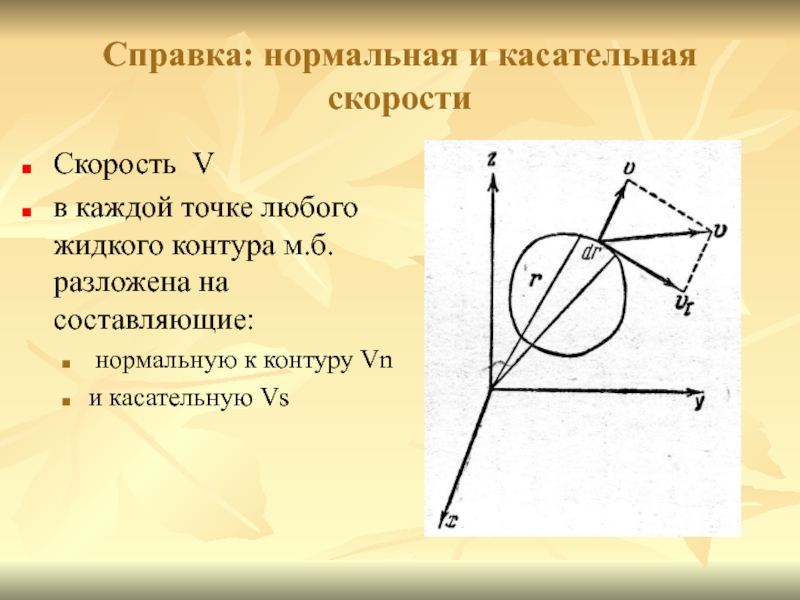
(очень малых) скорости вращения планетыСлайд 10Справка: нормальная и касательная скорости
Скорость V
в каждой точке любого
жидкого контура м.б. разложена на составляющие:
нормальную к контуру Vn
и касательную Vs
Слайд 11Справка: криволинейный интеграл
Определение
Способы вычисления: формула Грина
Независимость от пути интегрирования:
подынтегральное выражение – полный дифференциал некоторой функции F
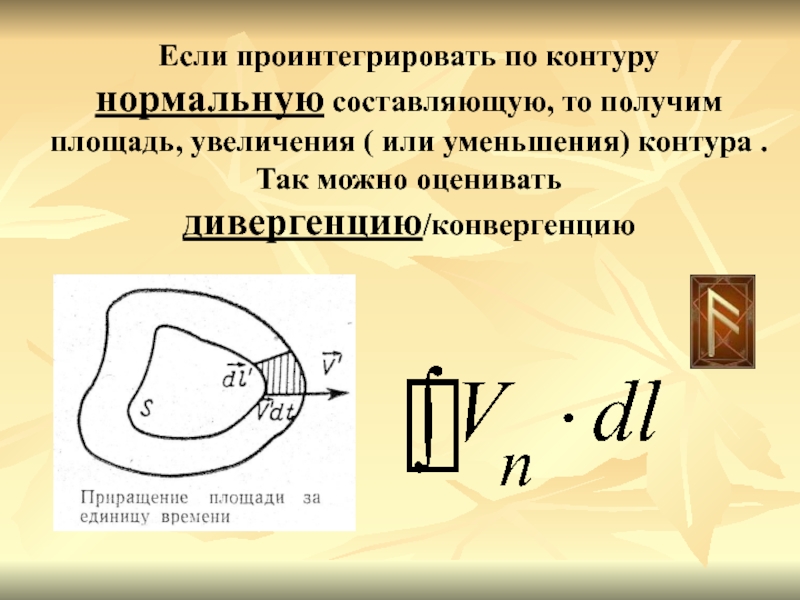
Слайд 12Если проинтегрировать по контуру нормальную составляющую, то получим площадь, увеличения
( или уменьшения) контура . Так можно оценивать дивергенцию/конвергенцию
Слайд 14циркуляция позволяет оценить угловой момент для частиц жидкости.
Действительно: если взять
круговой контур и считать, что жидкость обтекает его с постоянной
линейной скоростью V=Ωr , то получимПоэтому расчет циркуляции важен для метеорологических оценок
Внутреннее вращение в изолированной системе при сохранении общего углового момента должно изменять вращение остальных частей системы!
Пример: Если вращающееся колесо в руках повернуть осью вниз, то человек будет вращаться в противоположную сторону
Слайд 15Смысл: циркуляция показывает в какую сторону жидкость будет вращать гребное
колесо, в интересующей нас части жидкости
Чтобы колесо вращалось
не обязательно,
Чтобы
скорость на разных сторонах контура была направлена в разные стороныСлайд 16Свойства
1. Сумма циркуляций по контурам, у которых границы совпадают, равна
циркуляции по общей внешней границе
2. Циркуляция ускорения равна ускорению циркуляции
(Теорема Томсона)
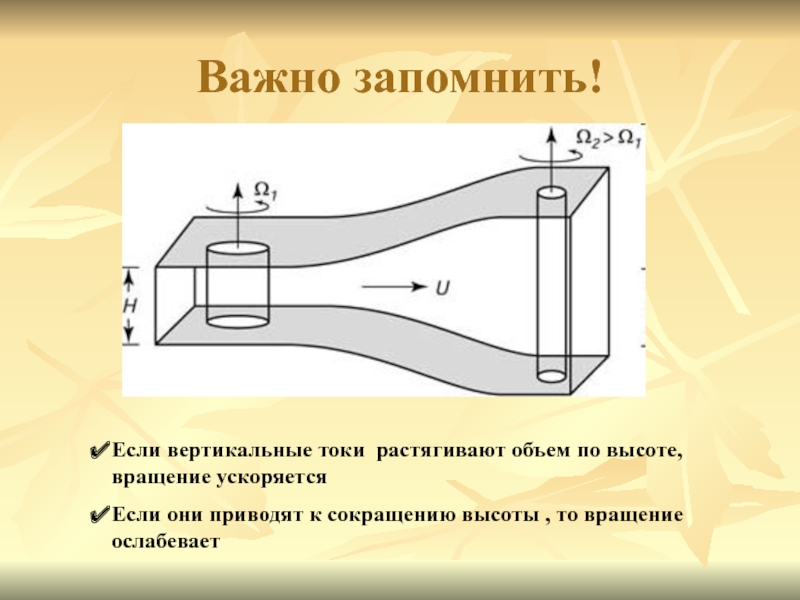
Слайд 18Важно запомнить!
Если вертикальные токи растягивают объем по высоте, вращение ускоряется
Если
они приводят к сокращению высоты , то вращение ослабевает
Слайд 20Важнейшей для нас фактор изменения циркуляции описывает
теорема Бьеркнеса
Изменение циркуляции (ускорение)
может происходить
Только за счет бароклинности атмосферы, когда изобарические и
изостерические (равной плотности) поверхности не параллельныСлайд 21Справка: доказательство теоремы Бьеркнеса
Если бы атмосфера не была бароклинна,
то не было бы фронтального циклогенеза !
Слайд 22Помнить: что бароклинность – причина циркуляции ?
Бароклинность – это зависимость
давления не только от плотности, но температуры
В атмосфере она проявляется
в форме изменения геострофическогоВетра, а значит и реального, ветра с высотой
- эффект «термического ветра» (см. рисунок)
Слайд 23Важное следствие:
В баротропной жидкости (ρ=F(p)) циркуляция по контуру, а значит
и момент импульса (вращения) частицы, не изменяются
Слайд 24Применение теоремы Бьеркнеса: направление и знак циркуляции
В математике издавна принято
(см.в начало) считать, что положительное направление обхода контура – это
такое, когда внешняя нормаль при обходе направлена вправо,т.е. контур остается слеваЭто обход против часовой стрелки!
По ветру, здесь: против часов!
Слайд 25Определение знака циркуляции по выделенному контуру изобаро-изострерических соленоидов.
Подсказка: а)определите
знак интеграла по контуру, выделенному стрелками на левом рисунке, затем
б) вспомните, что циркуляции элементарных контуров складываются, а потом в) учтите знак вклада бароклинности по теореме БьеркнесаСлайд 26Экзаменационный вопрос: вывести формулу для определения циркуляции по контуру, состоящему
из двух изобар и двух изотерм
Слайд 28Экзаменационный вопрос: вывести формулу для определения циркуляции по контуру, состоящему
из двух изобар и двух вертикалей
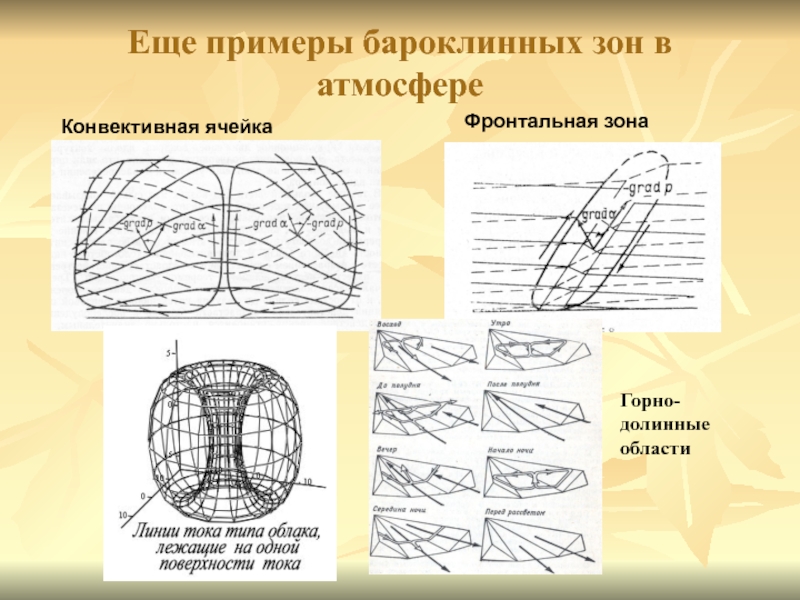
Слайд 29Еще примеры бароклинных зон в атмосфере
Конвективная ячейка
Фронтальная зона
Горно-долинные области
Слайд 30Экзаменационный вопрос: Оценить ускорение циркуляции в ячейке Гадлея, считая, что она
охватывает высоты от 1000 до 200 гПа, а разность температур
между экватором и полюсом 400ССчитая, что C≅V·πR≅V[м/с]·2·107[м], получим ускорение, которое получают ветви циркулирующего потока
Так что ячейка Гадлея имела бы очень большую скорость, если бы не …
Слайд 31Изменение циркуляция под влиянием трения
За счет трения одноименная циркуляция
всегда замедляется !
НО
Антициклон у земли усиливает циклон в средней атмосфере
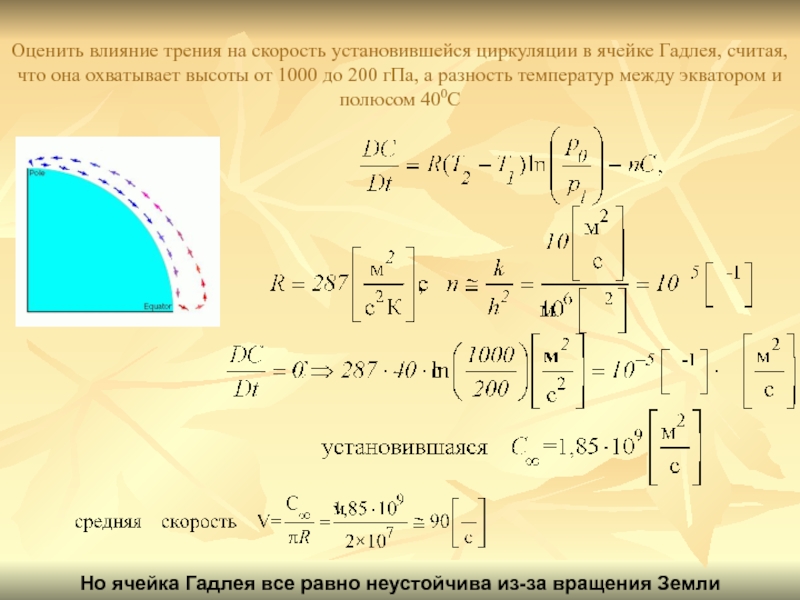
и наоборотСлайд 32Оценить влияние трения на скорость установившейся циркуляции в ячейке Гадлея,
считая, что она охватывает высоты от 1000 до 200 гПа,
а разность температур между экватором и полюсом 400СНо ячейка Гадлея все равно неустойчива из-за вращения Земли
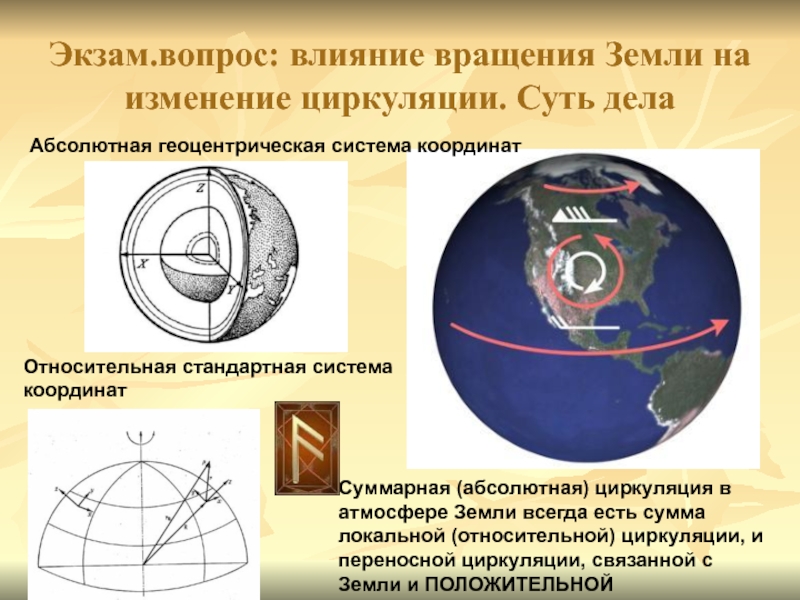
Слайд 33Экзам.вопрос: влияние вращения Земли на изменение циркуляции. Суть дела
Абсолютная геоцентрическая
система координат
Относительная стандартная система координат
Суммарная (абсолютная) циркуляция в атмосфере
Земли всегда есть сумма локальной (относительной) циркуляции, и переносной циркуляции, связанной с Земли и ПОЛОЖИТЕЛЬНОЙСлайд 34Экзам.вопрос: влияние вращения Земли на изменение циркуляции. Скорость переносного движения
Обратить
внимание: все выкладки в абсолютной системе координат!
Слайд 35Экзам.вопрос: влияние вращения Земли на изменение циркуляции. Циркуляция переносного движения
Обратить
внимание: все выкладки в абсолютной системе координат!
Циркуляция переносного движения равна
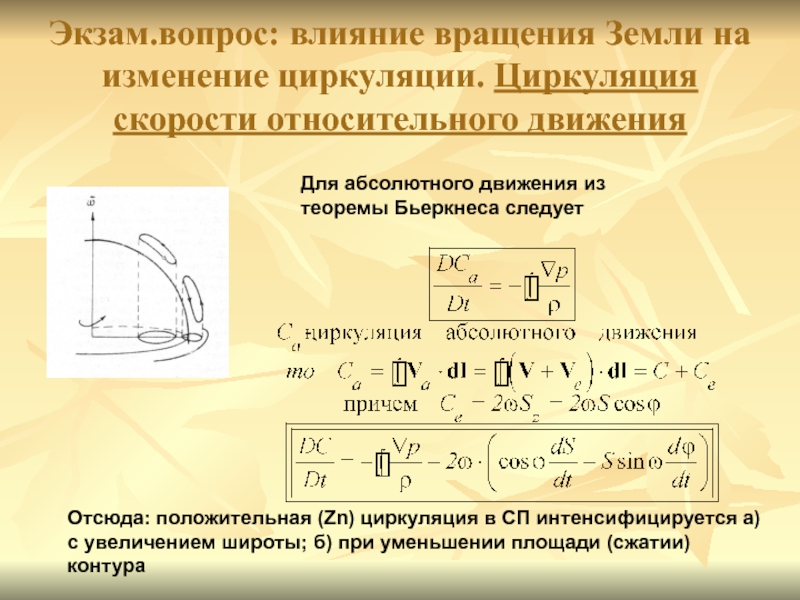
удвоенной угловой скорости Земли, умноженной на проекцию площади контура на экваториальную плоскостьСлайд 36Экзам.вопрос: влияние вращения Земли на изменение циркуляции. Циркуляция скорости относительного
движения
Для абсолютного движения из теоремы Бьеркнеса следует
Отсюда: положительная (Zn) циркуляция
в СП интенсифицируется а) с увеличением широты; б) при уменьшении площади (сжатии) контураСлайд 37Пример: влияние вращения Земли на изменение циркуляции
(лабораторная модель)
На вращающемся
против часовой стрелки диске крепится рамка из пластиковой трубки, в
которую налита вода.Если угол рамки уменьшить (как если бы контур приближался к экватору), то у стенок трубки изменяются линейные скорости вращения. Участок АВ ускоряется, а CD замедляется.
Вода в трубке по инерции на участке АВ отстает от стенок трубки, а на участке CD – обгоняет их.
Так возникает дополнительное вращение по часовой стрелке
(Циркуляция Уолеса в экваториальной зоне!)
Слайд 38Примеры влияния
изменения площади
В пассатах площадь к экватору усиливается и
антициклоничность циркуляции (субтропический Az) возрастает
При подходе циклона к невысокому хребту
он останавливается и начинает расширяться, т.к. скорость на ним хребтом возрастает. При этом циклоническая циркуляция уменьшается.При перетекании происходит обратный процесс
Слайд 39Задачи-минутки:
решил, значит все понял
Циклоническая и антициклоническая круговые изобары одинакового
радиуса расположены на одной и той же широте. По какой
из них больше циркуляция? (Zn)Вычислить значение переносной циркуляции на широте 600N вдоль изобары, охватывающей площадь 1 км2. (73 м2/с)
На широте 600N в антициклоне задан квадратный контур со стороной L=1000 км. Считая, что скорость ветра V на сторонах контура одинакова
вывести формулу для расчета циркуляции скорости абсолютного движения по этому контуру (Ca=2ωL2cosϕ-4VL)
определить ее значение так, чтобы циркуляция абсолютного движения по этому контуру оказалась равной нулю. (V=ωL/4≅18м/с).
Объяснить, что и в какую сторону измениться, если этот контур перенести без изменения на 70 широту (атм.баротропна)
Объяснить, что и в какую сторону измениться, если сторону этотго контура уменьшить вдвое (широта 60, атм.баротропна).
Слайд 40Не по теме –
задачи из вопросов 3 билетов.
Вычислить: Угловую
скорость вращения Земли
ω=2π/(24*3600)=7,29*10-5 [с-1]
Вычислить: Линейную скорость вращения Земли на экваторе.
U=R
ωcos(0)=6,4*106* 7,29*10-5 =466 [м с-1]Слайд 41Не по теме –
задачи из вопросов 3 билетов.
Вычислить: Газовую
постоянную сухого воздуха при нормальных условиях
R=P/(ρT)=100000[Нм-2]/1,28[кг м3]/273[K]=287[м2с-2К-1]
Вычислить: Плотность воздуха у
земли в стандартной атмосфереρ=P/RT=100000[Нм-2]/287[м2с-2К-1]/273[K-1]
Слайд 42Не по теме –
задачи из вопросов 3 билетов.
Вычислить: Массу
единичного столба атмосферы по давлению
M0=P/g=100000[кг/(мс2)]/10[м/с2]=104[кг/м2]
Вычислить: Массу атмосферы по давлению
Ма=M0*S=P/g*(4πR2)=104[кг/м2]*510*1014[м2]=
=5,1*1020[кг]Слайд 43Не по теме –
задачи из вопросов 3 билетов.
Вычислить: Насыщающее
давление водяного пара при кипении воды
Е=6,11*10[7,63*100/(242+100)]=1040[гПа]
Вычислить: Насыщающее давление водяного пара
при температуре 200СЕ=6,11*10[7,63*20/(242+20)]=23,4[гПа]































![Циркуляция Не по теме – задачи из вопросов 3 билетов.Вычислить: Угловую скорость Не по теме – задачи из вопросов 3 билетов.Вычислить: Угловую скорость вращения Землиω=2π/(24*3600)=7,29*10-5 [с-1]Вычислить: Линейную скорость](/img/thumbs/935f7f929a343c3e1aa0c7888c91b7ac-800x.jpg)
![Циркуляция Не по теме – задачи из вопросов 3 билетов.Вычислить: Газовую постоянную Не по теме – задачи из вопросов 3 билетов.Вычислить: Газовую постоянную сухого воздуха при нормальных условияхR=P/(ρT)=100000[Нм-2]/1,28[кг](/img/thumbs/308c7b8d4738d0405a0f62a82877f08c-800x.jpg)
![Циркуляция Не по теме – задачи из вопросов 3 билетов.Вычислить: Массу единичного Не по теме – задачи из вопросов 3 билетов.Вычислить: Массу единичного столба атмосферы по давлениюM0=P/g=100000[кг/(мс2)]/10[м/с2]=104[кг/м2]Вычислить: Массу](/img/thumbs/329e1f53355aa916afd114b7426d6359-800x.jpg)
![Циркуляция Не по теме – задачи из вопросов 3 билетов.Вычислить: Насыщающее давление Не по теме – задачи из вопросов 3 билетов.Вычислить: Насыщающее давление водяного пара при кипении водыЕ=6,11*10[7,63*100/(242+100)]=1040[гПа]Вычислить:](/img/thumbs/202ddf180e2e6783429be38a39dce832-800x.jpg)