Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Demand assessment elementary methods 1
Содержание
- 1. Demand assessment elementary methods 1
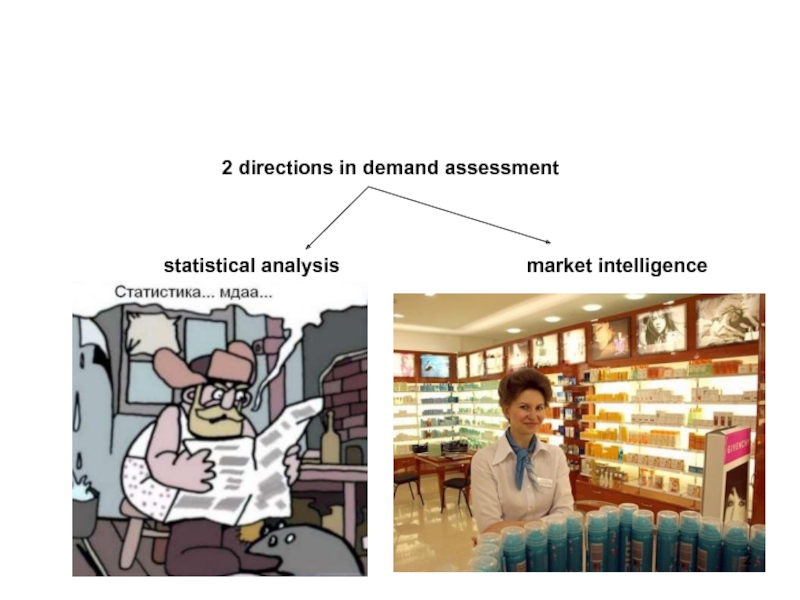
- 2. 2 directions in demand assessmentstatistical analysismarket intelligenceЗадача
- 3. Statistical analysisSteps:1) Collection, validation and assessment of
- 4. 1) Collection, validation and assessment of datatime seriescross-sectional dataStatistical analysis
- 5. time series1) Collection, validation and assessment
- 6. Adjustment of necessary information in order to
- 7. Statistical analysis1) Collection, validation and assessment of
- 8. Ex: In order to determine the effect
- 9. Statistical analysis2) The choice of the information
- 10. When choosing a curve there are two
- 11. If the trend of the experimental values
- 12. If the data can be reduced to
- 13. If the trend of the dependent variable
- 14. simple linear regressionSTEP 1. Data collectionTASK: TO
- 15. STEP 2. Organization variables in timesimple linear
- 16. simple linear regressionSTEP 3. Organization of a
- 17. simple linear regressionSTEP 4. Evaluation of the
- 18. simple linear regressionSTEP 4. Evaluation of the regression linePeriodObserva-tion XObserva-tion XObserva-tion YSumAverage
- 19. simple linear regressionSTEP 5. Comparison of calculated
- 20. simple linear regressionInterpretation of parametersThe "a" parameter
- 21. simple linear regressionEvaluation of the regression equationHow
- 22. The root – mean - square error
- 23. The root - mean - square error
- 24. The more root-mean-square error is, the greater
- 25. coefficient of determination, r^2Shows how well the
- 26. the correlation coefficient, r, Determines the degree of connection between variables-1 < r > 1
- 27. Слайд 27
- 28. Скачать презентанцию
2 directions in demand assessmentstatistical analysismarket intelligenceЗадача статистического анализа: определение параметров функции спроса посредством использования эмпирических данныхПри отсутствии надежной экспериментальной информации необходимо предпринять исследование рынка
Слайды и текст этой презентации
Слайд 22 directions in demand assessment
statistical analysis
market intelligence
Задача статистического анализа: определение
параметров функции спроса посредством использования эмпирических данных
информации необходимо предпринять исследование рынка
Слайд 3Statistical analysis
Steps:
1) Collection, validation and assessment of data
2) The choice
of the information curve
3) Verification and evaluation of the selected
curve
Слайд 41) Collection, validation and assessment of data
time series
cross-sectional data
Statistical analysis
Слайд 5 time series
1) Collection, validation and assessment of data
Statistical analysis
Examine
time changes in the demand for certain types of goods
or services and the corresponding time changes in pricing, sales volume and other independent variables that affect the demand
Слайд 6Adjustment of necessary information
in order to avoid effects such
as inflation
Deflationary correction: divide all nominal figures by the consumer
price index and multiplied by 100. Get "regular money" base periodAnd also it is necessary to take into account changes in population, accounting for seasonal and cyclical fluctuations
Long time period
time series
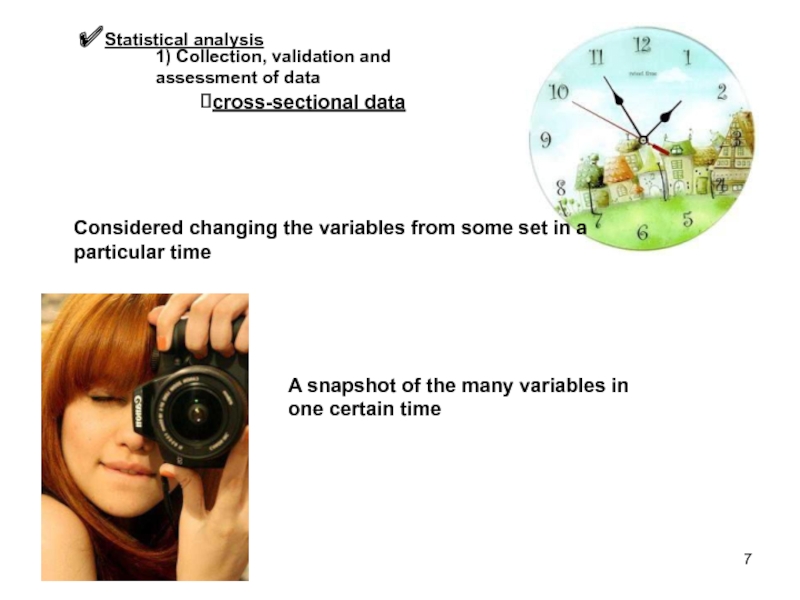
Слайд 7Statistical analysis
1) Collection, validation and assessment of data
cross-sectional data
Considered changing
the variables from some set in a particular time
A snapshot
of the many variables in one certain time
Слайд 8Ex: In order to determine the effect of prices on
demand, as a variable can be selected volume of sales
for a particular month,while the set may include a list of firms producing the product
Слайд 9Statistical analysis
2) The choice of the information curve
The results of
the observations are used to estimate the parameters of demand
functionThis function can then be used to predict values for the dependent variable for known values of the independent variables
Слайд 10When choosing a curve there are two main questions:
What type
of equation it is necessary to use?
How the selected function
fits and predicts the demand?The choice of the equation depends on two conditions:
а) the number of independent variables and б) the distribution of the data, i.e. linear or nonlinear distribution
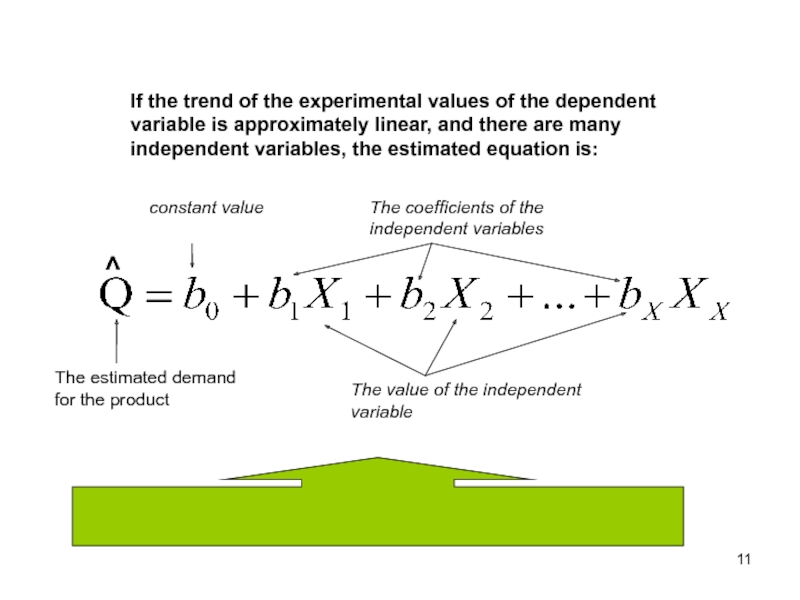
Слайд 11If the trend of the experimental values of the dependent
variable is approximately linear, and there are many independent variables,
the estimated equation is:The estimated demand for the product
The value of the independent variable
constant value
The coefficients of the independent variables
˄
Слайд 12If the data can be reduced to a single independent
variable (e.g. price) and the trend is almost linear than
to find the formula for this straight line we can use simple (pair) regression analysisThe equation thus is:
The quantity X,
(dependent variable)
The unit price of X (independent variable)
A constant value (which determines the point of intersection of the graph of the function with the Y axis)
The regression coefficient for Px (defining the slope of a line on the graph of a function)
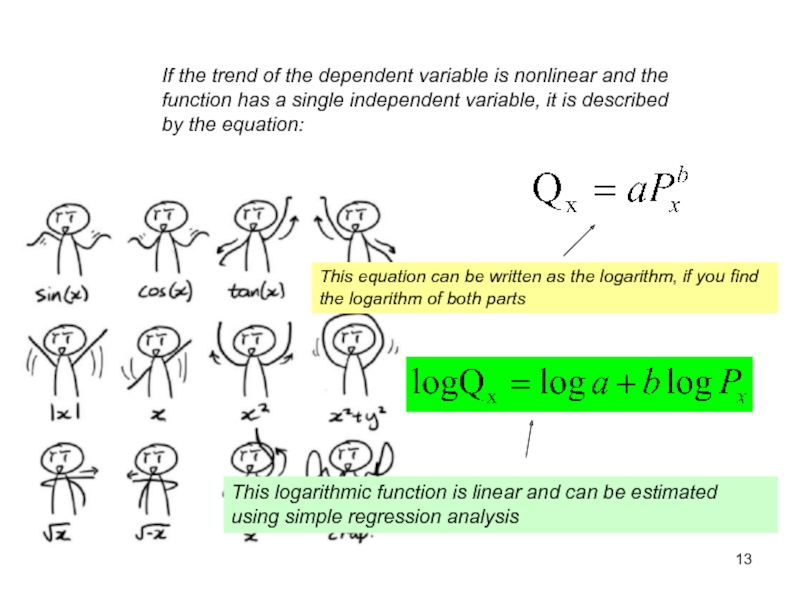
Слайд 13If the trend of the dependent variable is nonlinear and
the function has a single independent variable, it is described
by the equation:This equation can be written as the logarithm, if you find the logarithm of both parts
This logarithmic function is linear and can be estimated using simple regression analysis
Слайд 14simple linear regression
STEP 1. Data collection
TASK: TO FIND THE REGRESSION
FUNCTION for THESE DATA!
Collect time series data
Period
Observation X
Observation Y
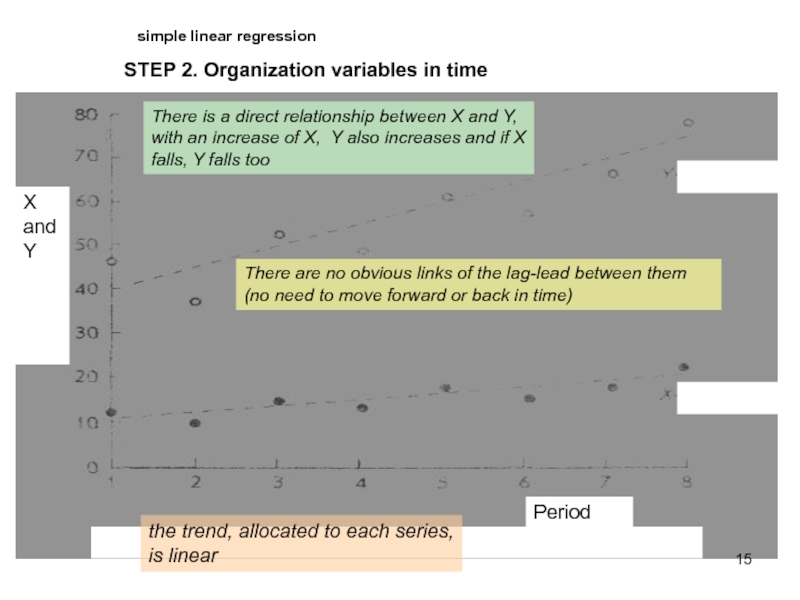
Слайд 15STEP 2. Organization variables in time
simple linear regression
Причины: визуализация; определение
линейности или нелинейности для выбора соответствующей формы кривой
Period
X and Y
There
is a direct relationship between X and Y, with an increase of X, Y also increases and if X falls, Y falls tooThere are no obvious links of the lag-lead between them (no need to move forward or back in time)
the trend, allocated to each series, is linear
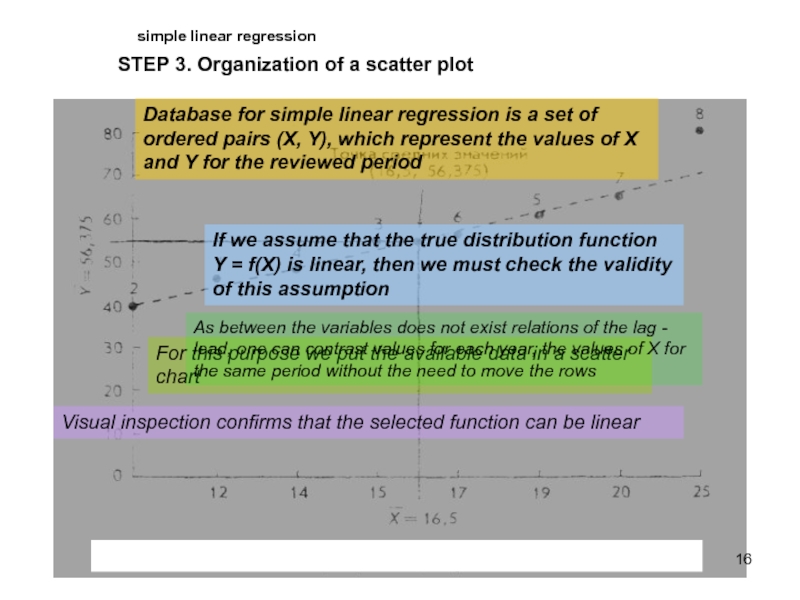
Слайд 16simple linear regression
STEP 3. Organization of a scatter plot
Database for
simple linear regression is a set of ordered pairs (X,
Y), which represent the values of X and Y for the reviewed periodIf we assume that the true distribution function Y = f(X) is linear, then we must check the validity of this assumption
For this purpose we put the available data in a scatter chart
As between the variables does not exist relations of the lag - lead, one can contrast values for each year, the values of X for the same period without the need to move the rows
Visual inspection confirms that the selected function can be linear
Слайд 17simple linear regression
STEP 4. Evaluation of the regression line
When making
the regression analysis we use the method of least squares
Minimizing
the sum of quadratic deviations of calculated Y values from its observed valuesIn order to estimate the true regression line Уi = а + b Хi, parameters a and b should be calculated for the estimated regression
Слайд 18simple linear regression
STEP 4. Evaluation of the regression line
Period
Observa-tion X
Observa-tion
X
Observa-tion Y
Sum
Average
Слайд 19simple linear regression
STEP 5. Comparison of calculated and actual values
How
well our estimated regression equation describes Y as a function
of X?Compare the actual and estimated value
The deviation of the actual values from the calculated values: the results of all observations do not fit on the regression line
The fact that the observations deviate from the regression line indicates that the magnitude of Y is effected also by forces different from X
Initial X
Initial Y
Estimated function
Deviation
Слайд 20simple linear regression
Interpretation of parameters
The "a" parameter determines the point
of intersection of the regression line with the Y axis
"a"
has no economic sense in the demand equationOption "b" determines the slope of the regression line
"b" represents the individual contribution of each independent variable to the value of the dependent variable
The positive sign of the parameter "b" indicates that the variables change in the same direction
Слайд 21simple linear regression
Evaluation of the regression equation
How informative or accurate
the determined Y is?
˄
When analyzing simple regression use two statistical
indicators:The root - mean - square error of the estimation, Se;
The coefficient of determination, r^2, and its square root, r, which is called the correlation coefficient.
The goal of linear regression evaluation: to get a linear equation, which can be used to determine the values of the independent variable Y on any existing values of the independent variable X
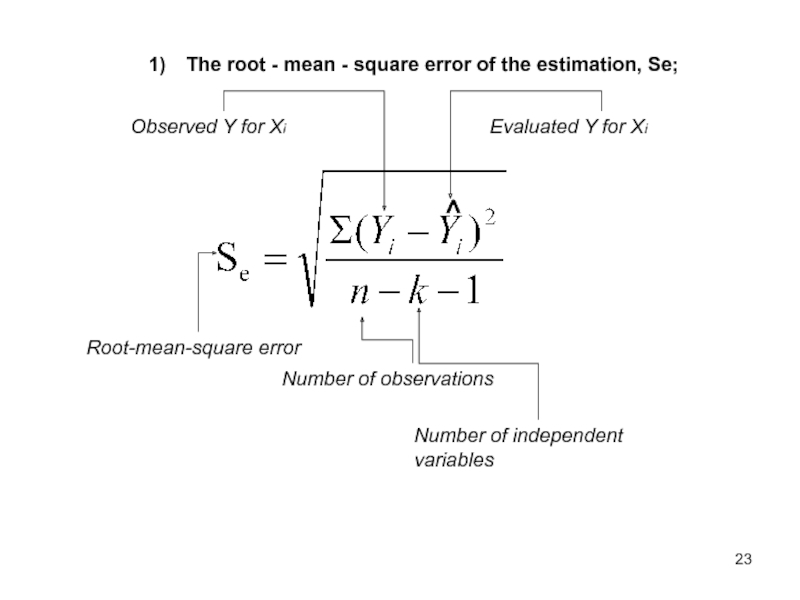
Слайд 22The root – mean - square error of the estimation,
Se;
Represents the deviation of experimental points from the estimated regression
line (determines the variance of random Y values)
Слайд 23The root - mean - square error of the estimation,
Se;
˄
Root-mean-square error
Observed Y for Xi
Evaluated Y for Xi
Number of observations
Number
of independent variables
Слайд 24The more root-mean-square error is, the greater the range of
deviations are
Root-mean-square error, Se;
If Se = 0, than the estimated
equation fits perfectly the observed data (all points lie on the regression line) 
Слайд 25coefficient of determination, r^2
Shows how well the regression model describes
the variation of the dependent variable
ЕХ: if r^2 = 0,975,
than approximately 97.5% of the changes in the dependent variable explained by the variation of the independent variable XValues can range from 0 to 1 or from 0 to 100%
0 - there is no relationship between the variables,
1 - the regression line is perfect (all changes are explained by changes in X)
Слайд 26the correlation coefficient, r,
Determines the degree of connection between
variables
-1 < r > 1
