Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Деривативи
Содержание
- 1. Деривативи
- 2. ПроблематикаВиди похідних інструментів та їх використанняВикористання свопівХарактеристика опціонів та їх видиОптимальний хеджСправедлива ціна опціонуМоделі ціноутворення опціонів
- 3. Види похідних інструментівта їх використання
- 4. Використання свопів
- 5. Елементи політики використання свопів (інших похідних) для
- 6. Як працюють опціониДилер отримує спред bid/offer, що
- 7. Кредитний свопКомпания А использует облигации с фиксированной
- 8. Розрахунки -1
- 9. Розрахунки -2: підприємство А
- 10. Розрахунки -3: підприємство Б
- 11. Характеристика опціонів та їх види
- 12. Види опціонівОпціон Call – гарантує право власника
- 13. Допущення ринку опціонівДля оцінки опціонів, що обертаються
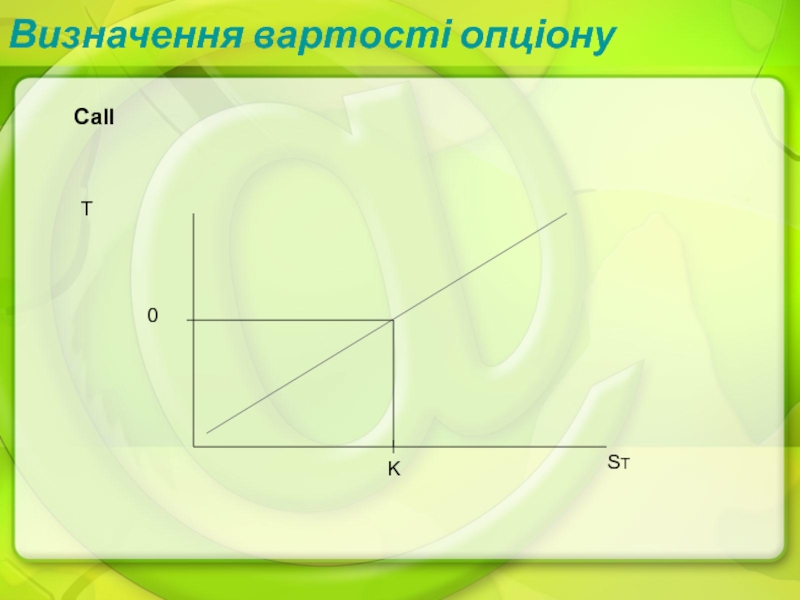
- 14. Визначення вартості опціонуCallST0TK
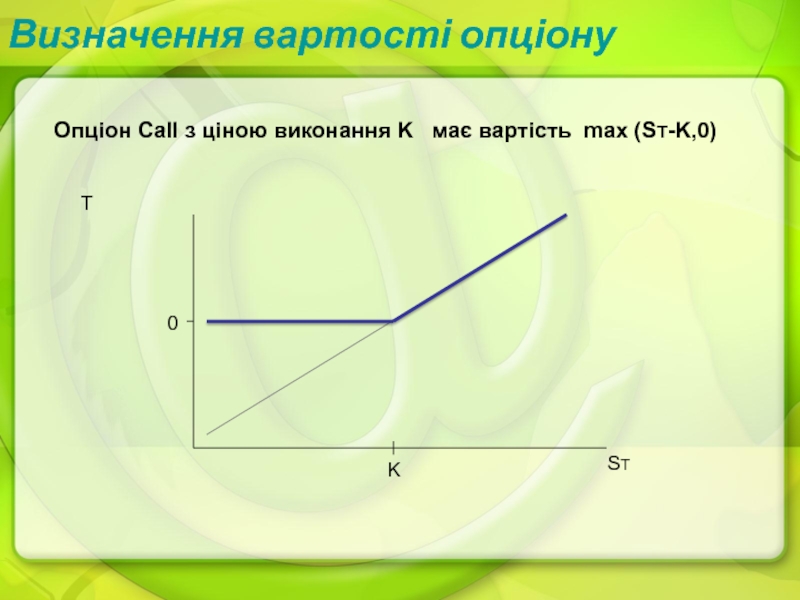
- 15. Визначення вартості опціонуОпціон Call з ціною виконання K має вартість max (ST-K,0)ST0KT
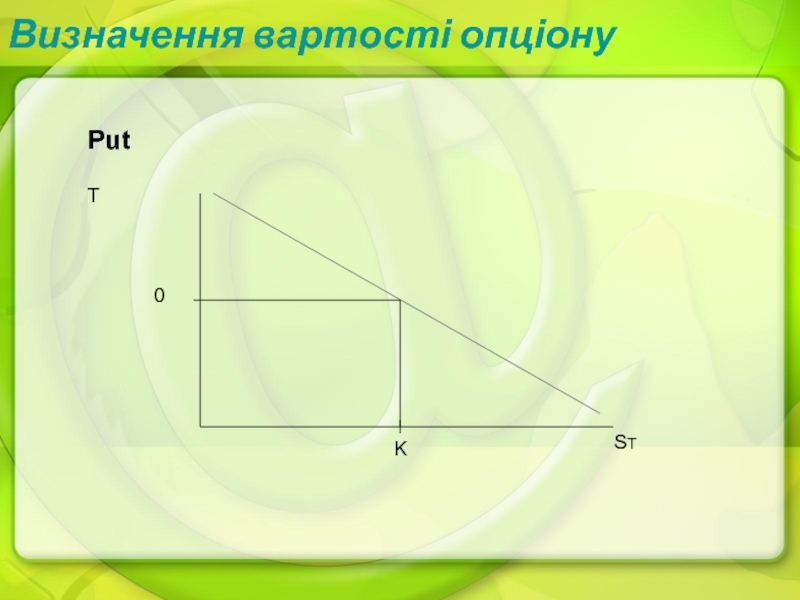
- 16. Визначення вартості опціонуPutST0KT
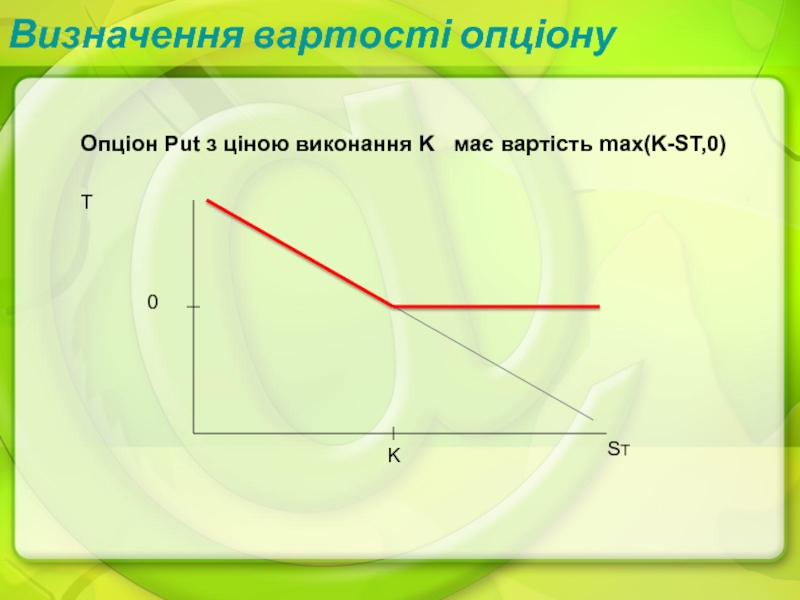
- 17. Визначення вартості опціонуОпціон Put з ціною виконання K має вартість max(K-ST,0)ST0KT
- 18. Паритетність Call та Put
- 19. ПрикладЦіна місячного опціну call із ціною виконання
- 20. Оптимальний хедж
- 21. ПрикладЦіна базового активу (акції) складає 100 грн.
- 22. Рівноважний підхідВартість активу із імовірністю 70% складе
- 23. Рівноважний підхідПрипустимо, що ціна виконання опціону call
- 24. Нейтральний до ризику підхідВАРІАНТИ:Ризик приведена імовірністьПсевдоімовірністьДисконтування приведених на ризик cash flows по безризиковій доходності
- 25. Нейтральний до ризику підхідРизик нейтральна імовірність (u)
- 26. Моделі ціноутворенняопціонів
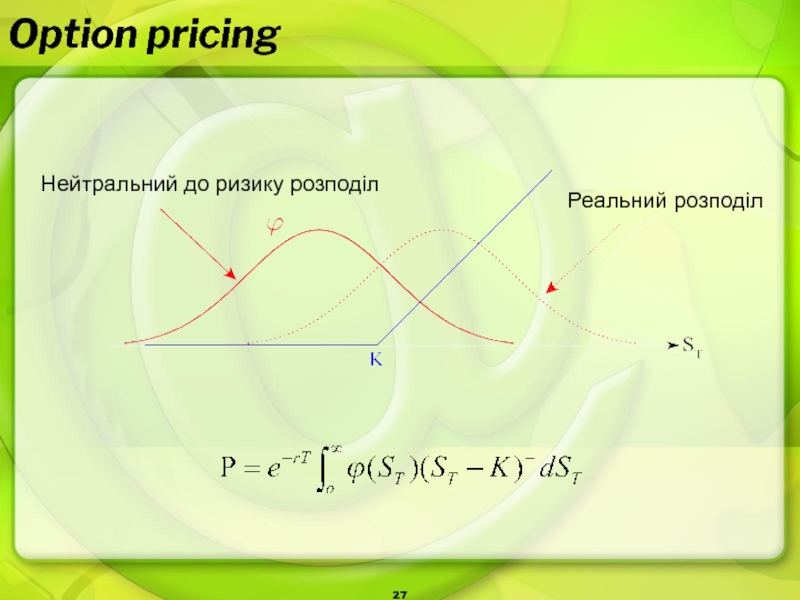
- 27. Option pricingНейтральний до ризику розподілРеальний розподіл
- 28. Історична волатильністьПриведене до річного базису середньоквадратичне відхилення
- 29. Біномінальне деревоЗапропонований у 1979 рцоі Cox, Ross,
- 30. Стандартне біномінальне деревоУстановлюються часові межі інтервалу аналізу,
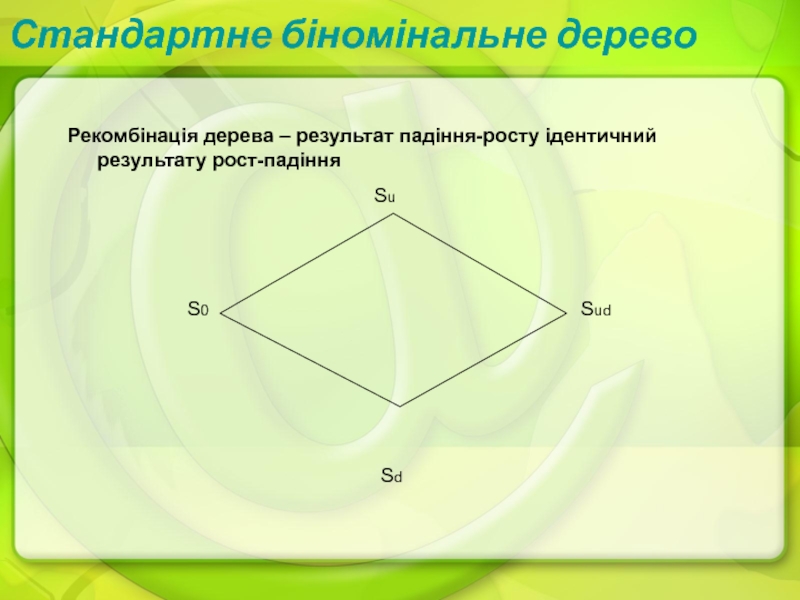
- 31. Стандартне біномінальне деревоРекомбінація дерева – результат падіння-росту ідентичний результату рост-падінняSd
- 32. Стандартне біномінальне деревоКоефіцієнти росту та падіння фіксовані
- 33. Визначенням параметрівОчікувана вартість базового активу та імовірнісні параметри:p – імовірність реалізації траєкторії росту.
- 34. Визначенням параметрівВолатильність:Для стандартизованого дерева:
- 35. Метод Cox, Ross, RubinsteiІз рівняння волатильності для
- 36. Метод рівних можливостейПриймемо, що імовірність росту чи падіння однакова і дорівнює p=0,5, відповідно:Із рівняння волатильності маємо:Відповідно,
- 37. Мотод Блека-Скоулза
- 38. Скачать презентанцию
ПроблематикаВиди похідних інструментів та їх використанняВикористання свопівХарактеристика опціонів та їх видиОптимальний хеджСправедлива ціна опціонуМоделі ціноутворення опціонів
Слайды и текст этой презентации
Слайд 2Проблематика
Види похідних інструментів та їх використання
Використання свопів
Характеристика опціонів та їх
види
Слайд 5Елементи політики використання свопів (інших похідних)
для ризик-мененджменту
Визначення цілей та завдань
Хеджування
– плаваюча ставка чи майбутні запозичення
Заощадження – більша ефективність відносно
традиційних інструментів фінансуванняСтруктурування – досягнення цілей, реалізація яких не можлива на традиційних ринках
Ідентифікація доступних інструментів
свопи
опціони (e.g. кепи, коллари, свопціони)
інвестиційні продукти
Авторизація
Розподіл відповідних повноважень
Фінансовий директор (CFO), казначей
Обмеження та ліміти
Загальна чутливість сторін
Специфічна чутливість сторін
Умови угоди
Вимоги сторін
Забезпечення
Транзакційні ризики
Ідентифікація
Аналіз
Оцінка та ціноутворення
Методологія придбання
Узгодження умов
Конкурентна пропозиція
Прийнятність
Ціноутворення справедливого ринку
Контроль та звітування
Оцінювання
Періодичне звітування
Слайд 6Як працюють опціони
Дилер отримує спред bid/offer, що склався на ринку
Спред
тим більший, чим триваліший спред і складніший продукт
Спред компенсує такі
ринкові витрати дилера: витрати на хеджування портфеля свопів
залишковий ризик
вартість капіталу
Swaps дилер
Підприємство A
Підприємство B
Плаваюча ставка)
Фіксована ставка
(Offer))
Плаваюча ставка
Фіксована ставка
(Bid)
Слайд 7Кредитний своп
Компания А использует облигации с фиксированной ставкой 11 ½%,
а кредиты получает под LIBOR+3/8%. С другой стороны, компания Б
получает кредит под LIBOR+1 1/8%, а облигации выпускает под фиксированные 13%.Чем компаниям может помочь своп.
Слайд 12Види опціонів
Опціон Call – гарантує право власника придбати базовий актив
по фіксованій ціні у майбутньому.
Фіксована ціна базового активу називається ціною
виконання або strike price.Опціон Put – гарантує право власника продати базовий актив по фіксованій ціні у майбутньому.
Європейський опціон - може бути виконаний лише у момент завершення строку обігу опціону.
Американський опціон – може бути виконаний у будь-який момент протягом дії опціону.
Слайд 13Допущення ринку опціонів
Для оцінки опціонів, що обертаються на ринку, висуваються
такі припущення:
нема арбітражу
досконала конкуренція
нема bid-ask спреду
стабільні процентні ставки
є можливість
запозичення капіталу по безризиковій ставкипо базовому активу нема посивного доходу (наприклад, дивідендів)
Слайд 19Приклад
Ціна місячного опціну call із ціною виконання в 100 грн
складає 25 грн. Визначте ціну місячного опціну put за умови,
що безризикова доходність складає 3% при поточній вартості базового активу в 80 грн.
Слайд 21Приклад
Ціна базового активу (акції) складає 100 грн. Результати прогнозування свідчать,
що протягом місяця ціна може вирости або зменшитися на 20
грн. Визначте оптимальний хедж (кількість проданих опціонів) із використанням місячних опціонів із ціною виконання 100 грн.Безризикова доходність 5%.
Яка справедлива ціна такого опціону
Слайд 22Рівноважний підхід
Вартість активу із імовірністю 70% складе 200 грн. та
50 грн із імовірністю 30%. Безризикова ставка 10%, поточна вартість
активу – 100 грн.EP= 0,7 (200) + 0,3 (50) = 155
u = 200/100 = 2
d = 50/100 = 0.5
r = 1,10
RAR= 155/100 - 1 = 55%
Премія за ризик = 55% - 10% = 45%
Слайд 23Рівноважний підхід
Припустимо, що ціна виконання опціону call складає 120 грн.
із коефіцієнтом бета 1,83
Тоді:
EP = 0,7 (80) + 0,3 (0)
= 56Beta = b(C) = 1,83
RAR= r(C) = 10% + 1,83 (45%) = 92,5%
Вартість опціону = C = 56/(1,925) = 29.09
Слайд 24Нейтральний до ризику підхід
ВАРІАНТИ:
Ризик приведена імовірність
Псевдоімовірність
Дисконтування приведених на ризик cash
flows по безризиковій доходності
Слайд 25Нейтральний до ризику підхід
Ризик нейтральна імовірність (u) = 0,4
Ризик
нейтральна EP для акції =
0,4 (200) + 0,6 (50)
= 110Приведений курс акції = 110/1,10 = 100
Ризик нейтральна EP для опціону call =
0,4 (80) + 0,6 (0) = 32
Вартість опціону = 32/1,10 = 29,09
Слайд 29Біномінальне дерево
Запропонований у 1979 рцоі Cox, Ross, and Rubenstein.
Біномінальна модель
представляє собою дискретний процес, який більш гнучкий за модель безперервного
геометричного бруонівського руху.Розрізняють два види дерев:
стандартне – безпосередньо походить від моделі геометричного бруонівського руху; присутні обмеження
гнучке – без жодних обмежень
Слайд 30Стандартне біномінальне дерево
Установлюються часові межі інтервалу аналізу, який ділиться на
менші інтервали.
Для завершення кожного із інтервалу визначається варіанти ціни базового
активу.Для кожного моменту часу існують два варіанти – зростання та падіння.
Рух на зростання та падіння визначається волатильністю базового активу.
Рух на зростання та падіння оцінюється як відношення нової ціни на кінець інтервалу до її початкового значення.
Слайд 31Стандартне біномінальне дерево
Рекомбінація дерева – результат падіння-росту ідентичний результату рост-падіння
Sd
Слайд 32Стандартне біномінальне дерево
Коефіцієнти росту та падіння фіксовані як і імовірність
подій.
Довжина інтервалу незмінна.
Дерево є рекомбінаційним.
Дерево централізоване:
d=1/u
Умова централізації:
ud = e2rΔt
Слайд 33Визначенням параметрів
Очікувана вартість базового активу та імовірнісні параметри:
p – імовірність
реалізації траєкторії росту.
Слайд 35Метод Cox, Ross, Rubinstei
Із рівняння волатильності для стандартного дерева:
Відповідно до
умови централізації:
d=1/u
Із рівняння очікуваної вартості активу для стандартного дерева :
Слайд 36Метод рівних можливостей
Приймемо, що імовірність росту чи падіння однакова і
дорівнює p=0,5, відповідно:
Із рівняння волатильності маємо:
Відповідно,
