Дифракция

законов геометрической оптики.
Благодаря дифракции волны могут попадать в

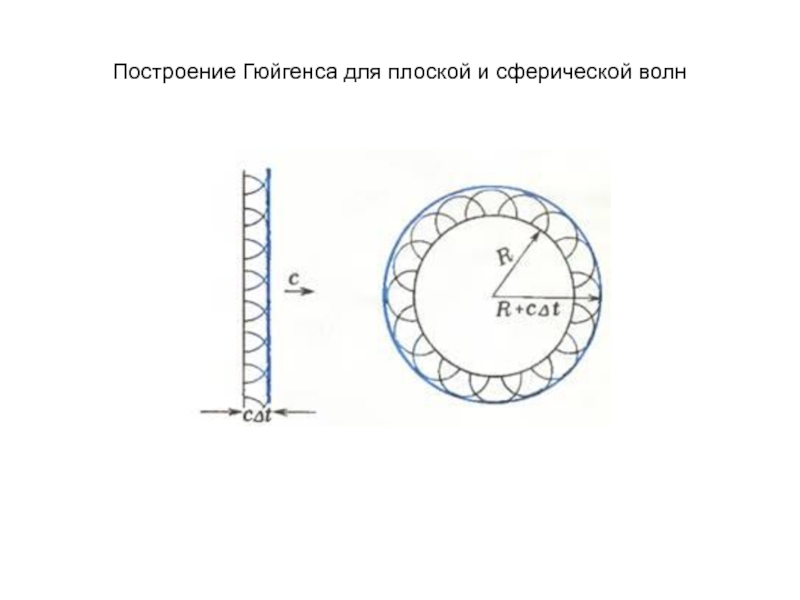
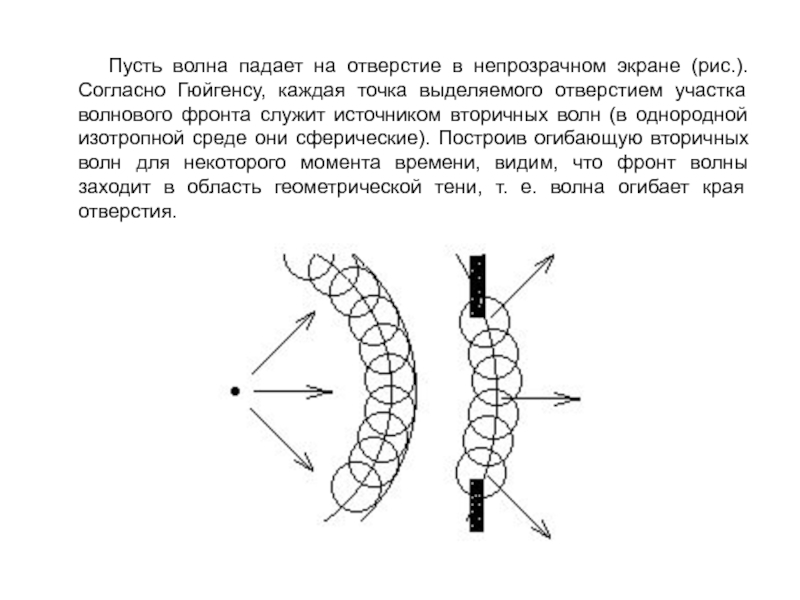
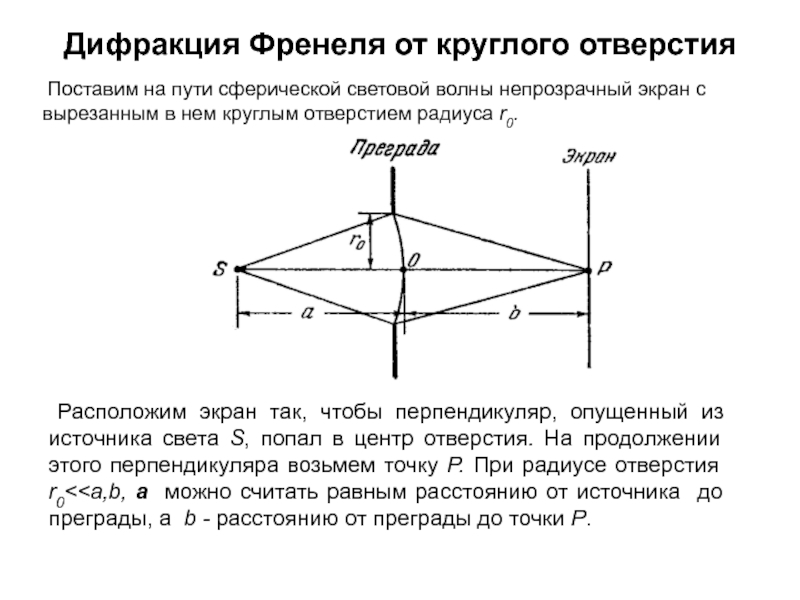
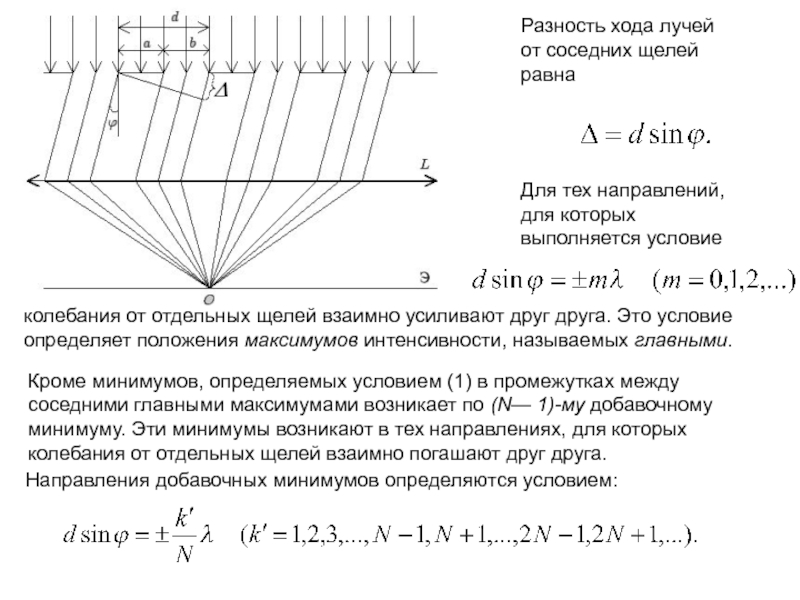
Явление дифракции объясняется с помощью принципа Гюйгенса (1690 г.), согласно которому каждая точка, до которой доходит волна, является источником вторичных сферических волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

Волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t.

(рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта

позволяет найти амплитуду, а следовательно, и интенсивность волн, распространяющихся по

Недостатки:

Френель дополнил принцип Гюйгенса идеей об интерференции вторичных волн.

волнового фронта, являются источниками когерентных вторичных волн, а амплитуда колебаний

Пусть S - волновая поверхность. Для нахождения напряженности поля E в произвольной точке P разобьем волновую поверхность на элементарные участки dS. Каждый из этих участков становится источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента dS и обратно пропорциональна расстоянию r от элемента до точки P

Eo - амплитуда первичной волны в точках волнового фронта; 

Результирующее колебание приходящее от всех точек волновой поверхности определяется соотношением

что если между источником и точкой наблюдения находится непрозрачный экран

В общем случае расчет интерференции вторичных волн с использованием записанного интеграла представляет сложную задачу, однако для некоторых симметричных случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.

возбуждаемого в точке P сферической волной, распространяющейся в однородной среде

Волновая поверхность такой волны симметрична относительно прямой SP, Френель разбил волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки P отличаются на /2 ( - длина волны в той среде, в которой распространяется волна).

можно представить следующим образом:
где b - расстояние от вершины волновой

разность фаз
и гасить друг друга.
Для оценки амплитуд

где Sm-1 - площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны.

радиус внешней границы m-й зоны.
Возведя скобки в квадрат, получим

малости  пренебречь слагаемым, содержащим 2. В этом приближении
Площадь сферического

R — радиус сферы, h - высота сегмента).

- ой зоны Френеля
Полученное выражение не зависит от m. Следовательно,

высота сегмента hm

первой (центральной) зоны получается значение: r1=0,5 мкм. Радиусы последующих зон

Расстояние bm от зоны до точки P медленно растет с по линейному закону. Угол  между нормалью к элементам зоны и направлением на точку P также растет с номером зоны m. Все это приводит к тому, что амплитуда колебания Em, возбуждаемого m-й зоной в точке P, монотонно убывает с ростом m.

Таким образом, амплитуды колебаний, возбуждаемых в точке зонами Френеля, образуют монотонно убывающую последовательность:

амплитуда результирующего светового колебания в точке может быть найдена алгебраически:
В

Вследствие монотонного убывания Em можно приближенно считать, что

При этом условии выражения, заключенные в круглые скобки, будут равны нулю, и формула упрощается следующим образом:

сферической волновой поверхностью, равна половине амплитуды, создаваемой одной центральной зоной,

опущенный из источника света S, попал в центр отверстия. На

m первых зон Френеля, построенных для точки P.
Если расстояния a

Выразив m, получим число открытых зон Френеля:

Амплитуда колебания в точке P будет равна:

В этом выражении амплитуда Em берется со знаком плюс, если т нечетное, и со знаком минус, если т четное.

круглые скобки, можно считать равными нулю. Амплитуды от двух соседних

Поэтому

В результате получится:

где знак «плюс» берется для нечетных m и минус «минус» - для четных.

зон Френеля амплитуда в точке будет максимальна и приближенно равна

Дифракция Френеля на круглом отверстии

m=2

m=3

m=4

m=5

m=6

и точкой наблюдения P круглый непрозрачный диск радиуса r0.

Значит интенсивность света в центре геометрической тени отлична от нуля. Таким образом, теория Френеля предсказывает проникновение света в центр геометрической тени диска. Светлое пятно в центре тени получило название «пятно Пуассона».

диаметра диска

мере ее расширения.
     Начальная ширина соответствует примерно одной открытой полуволновой зоне,

Пусть на бесконечно длинную щель падает плоская световая волна. Поместим

Все параллельные лучи, падающие на линзу под углом  к ее оптической оси , перпендикулярной к фронту падающей волны, соберутся в точке B зкрана. Оптическая разность хода между крайними лучами MC и DF, идущими от щели в этом направлении, равна

щели так, что оптическая разность хода лучей, проведенных из краев

При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.

Результат интерференции света в точке B определяется тем, сколько зон Френеля укладывается в щели.

зон нечетное:
то наблюдается дифракционный максимум.
Величина m называется порядком дифракционного

В направлении =0 наблюдается самый интенсивный центральный максимум нулевого порядка.

расширения слева направо.
Размер области дифракционного расплывания обратно пропорционален ширине

(случай плоской световой волны), тогда
Воспользуемся этим соотношением, как критерием

– геометрическая оптика

от геометрической оптики (1-3) через дифракцию Френеля (4-7) к дифракции

равной ширины, лежащих в одной плоскости и разделенных равными по

b - ширина каждой щели.

Пусть a - ширина непрозрачных участков между щелями,

Величина d=a+b называется периодом дифракционной решетки

N - число щелей

решетки
(1)
Пусть на дифракционную решётку падает плоская монохроматическая волна.

для которых выполняется условие
колебания от отдельных щелей взаимно усиливают

Кроме минимумов, определяемых условием (1) в промежутках между соседними главными максимумами возникает по (N— 1)-му добавочному минимуму. Эти минимумы возникают в тех направлениях, для которых
колебания от отдельных щелей взаимно погашают друг друга.

Направления добавочных минимумов определяются условием:

приходящееся на промежуток между соседними главными максимумами, равно N —

Так как модуль sin не может быть больше единицы, то из условия максимумов следует, что число главных максимумов определяется соотношением

N=4, d/b=3

дневного света