Слайд 1Динамические структуры данных
(язык Паскаль)
© К.Ю. Поляков, 2008-2010
Указатели
Динамические массивы
Структуры
Списки
Стеки, очереди, деки
Деревья
Графы
Слайд 2Тема 1. Указатели
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
Слайд 3Статические данные
переменная (массив) имеет имя, по которому к ней можно
обращаться
размер заранее известен (задается при написании программы)
память выделяется при
объявлении
размер нельзя увеличить во время работы программы
var x, y: integer;
z: real;
A: array[1..10] of real;
str: string;
Слайд 4Динамические данные
размер заранее неизвестен, определяется во время работы программы
память выделяется
во время работы программы
нет имени?
Проблема:
как обращаться
к данным, если нет имени?
Решение:
использовать адрес в памяти
Следующая проблема:
в каких переменных могут храниться адреса?
как работать с адресами?
Слайд 5Указатели
Указатель – это переменная, в которую можно записывать адрес другой
переменной (или блока памяти).
Объявление:
Как записать адрес:
var pC:
^char; // адрес символа
pI: ^integer; // адрес целой переменной
pR: ^real; // адрес вещ. переменной
var m: integer; // целая переменная
pI: ^integer; // указатель
A: array[1..2] of integer; // массив
...
pI:= @ m; // адрес переменной m
pI:= @ A[1]; // адрес элемента массива A[1]
pI:= nil; // нулевой адрес
@
^
nil
указатель
адрес ячейки
Слайд 6Обращение к данным через указатель
program qq;
var m, n: integer;
pI: ^integer;
begin
m := 4;
pI := @m;
writeln('Адрес m
= ', pI); // вывод адреса
writeln('m = ', pI^); // вывод значения
n := 4*(7 - pI^); // n = 4*(7 - 4) = 12
pI^ := 4*(n - m); // m = 4*(12 – 4) = 32
end.
^
«вытащить» значение по адресу
Слайд 7Обращение к данным (массивы)
program qq;
var i: integer;
A: array[1..4]
of integer;
pI: ^integer;
begin
for i:=1 to 4 do
A[i] := i;
pI := @A[1]; // адрес A[1]
while ( pI^ <= 4 ) // while( A[i] <= 4 )
do begin
pI^ := pI^ * 2; // A[i] := A[i]*2;
pI := pI + 1; // к следующему элементу
end;
end.
переместиться к следующему элементу = изменить адрес на sizeof(integer)
Слайд 8Что надо знать об указателях
указатель – это переменная, в которой
можно хранить адрес другой переменной;
при объявлении указателя надо указать тип
переменных, на которых он будет указывать, а перед типом поставить знак ^ ;
знак @ перед именем переменной обозначает ее адрес;
запись p^ обозначает значение ячейки, на которую указывает указатель p;
nil – это нулевой указатель, он никуда не указывает
при изменении значения указателя на n он в самом деле сдвигается к n-ому следующему числу данного типа (для указателей на целые числа – на n*sizeof(integer) байт).
Слайд 9Тема 2. Динамические массивы
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
Слайд 10Где нужны динамические массивы?
Задача. Ввести размер массива, затем – элементы
массива. Отсортировать массив и вывести на экран.
Проблема:
размер массива заранее
неизвестен.
Пути решения:
выделить память «с запасом»;
выделять память тогда, когда размер стал известен.
Алгоритм:
ввести размер массива;
выделить память ;
ввести элементы массива;
отсортировать и вывести на экран;
удалить массив.
выделить память
удалить массив
Слайд 11Использование указателей (Delphi)
program qq;
type intArray = array[1..1] of integer;
var A:
^intArray;
i, N: integer;
begin
writeln('Размер массива>');
readln(N);
GetMem(pointer(A), N*sizeof(integer));
for i := 1 to N do
readln(A[i]);
... { сортировка }
for i := 1 to N do
writeln(A[i]);
FreeMem(pointer(A));
end.
выделить память
освободить память
работаем так же, как с обычным массивом!
какой-то массив целых чисел
Слайд 12Использование указателей
для выделения памяти используют процедуру GetMem
GetMem( указатель,
размер в байтах );
указатель должен быть приведен к типу pointer
–указатель без типа, просто адрес какого-то байта в памяти;
с динамическим массивом можно работать так же, как и с обычным (статическим);
для освобождения блока памяти нужно применить процедуру FreeMem:
FreeMem ( указатель );
Слайд 13Ошибки при работе с памятью
Запись в «чужую» область памяти:
память не
была выделена, а массив используется.
Что делать: так не делать.
Выход за
границы массива:
обращение к элементу массива с неправильным номером, при
записи портятся данные в «чужой» памяти.
Что делать: если позволяет транслятор, включать проверку
выхода за границы массива.
Указатель удаляется второй раз:
структура памяти нарушена, может быть все, что угодно.
Что делать : в удаленный указатель лучше записывать nil,
ошибка выявится быстрее.
Утечка памяти:
ненужная память не освобождается.
Что делать : убирайте «мусор»
(в среде .NET есть сборщик мусора!)
Слайд 14Динамические массивы(Delphi)
program qq;
var A: array of integer;
i, N:
integer;
begin
writeln('Размер массива>');
readln(N);
SetLength ( A, N );
for
i := 0 to N-1 do
readln(A[i]);
... { сортировка }
for i := 0 to N-1 do
writeln(A[i]);
SetLength( A, 0 );
end.
выделить память
освободить память
какой-то массив целых чисел
нумерация с НУЛЯ!
Слайд 15Динамические массивы (Delphi)
при объявлении массива указывают только его тип, память
не выделяется:
var A: array of integer;
для выделения памяти
используют процедуру SetLength (установить длину)
SetLength ( массив, размер );
номера элементов начинаются с НУЛЯ!
для освобождения блока памяти нужно установить нулевую длину через процедуру SetLength:
SetLength ( массив, 0 );
Слайд 16Динамические матрицы (Delphi)
Задача. Ввести размеры матрицы и выделить для нее
место в памяти во время работы программы.
Проблема:
размеры матрицы заранее
неизвестны
Решение:
var A: array of array of integer;
N, M: integer;
begin
writeln('Число строк и столбцов>');
readln(N, M);
SetLength ( A, N, M );
... // работаем, как с обычной матрицей
SetLength( A, 0, 0 );
end.
Слайд 17Тема 3. Структуры (записи)
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
Слайд 18Структуры (в Паскале – записи)
Структура (запись) – это тип данных,
который может включать в себя несколько полей – элементов разных
типов (в том числе и другие структуры).
Свойства:
автор (строка)
название (строка)
год издания (целое число)
количество страниц (целое число)
Задача: объединить эти данные в единое целое
Размещение в памяти
Слайд 19Одна запись
readln(Book.author); // ввод
readln(Book.title);
Book.year := 1998; //
присваивание
if Book.pages > 200 then // сравнение
writeln(Book.author,
'.', Book.title); // вывод
Объявление (выделение памяти):
var Book: record
author: string[40]; // автор, строка
title: string[80]; // название, строка
year: integer; // год издания, целое
pages: integer; // кол-во страниц, целое
end;
название
запись
поля
Обращение к полям:
Слайд 20Массив записей
Объявление (выделение памяти):
const N = 10;
var aBooks: array[1..N] of
record
author: string[40];
title: string[80];
year: integer;
pages: integer;
end;
Books[1] ... Books[10]
Слайд 21Массив записей
for i:=1 to N do begin
readln(aBooks[i].author);
readln(aBooks[i].title);
...
end;
for i:=1 to N do
if aBooks[i].pages > 200
then
writeln(aBooks[i].author, '.',
aBooks[i].title);
Обращение к полям:
Слайд 22Новый тип данных – запись
const N = 10;
var Book: TBook;
// одна запись
aBooks: array[1..N] of TBook; // массив
Объявление
типа:
type TBook = record
author: string[40]; // автор, строка
title: string[80]; // название, строка
year: integer; // год издания, целое
pages : integer; // кол-во страниц, целое
end;
Объявление переменных и массивов:
TBook – Type Book («тип книга») – удобно!
Слайд 23Записи в процедурах и функциях
Book.author := 'А.С. Пушкин';
ShowAuthor ( Book
);
Book.year := 1800;
writeln( IsOld(Book) );
Процедура:
procedure ShowAuthor ( b: TBook );
begin
writeln ( b.author );
end;
Основная программа:
function IsOld( b: TBook ): boolean;
begin
IsOld := b.year < 1900;
end;
Функция:
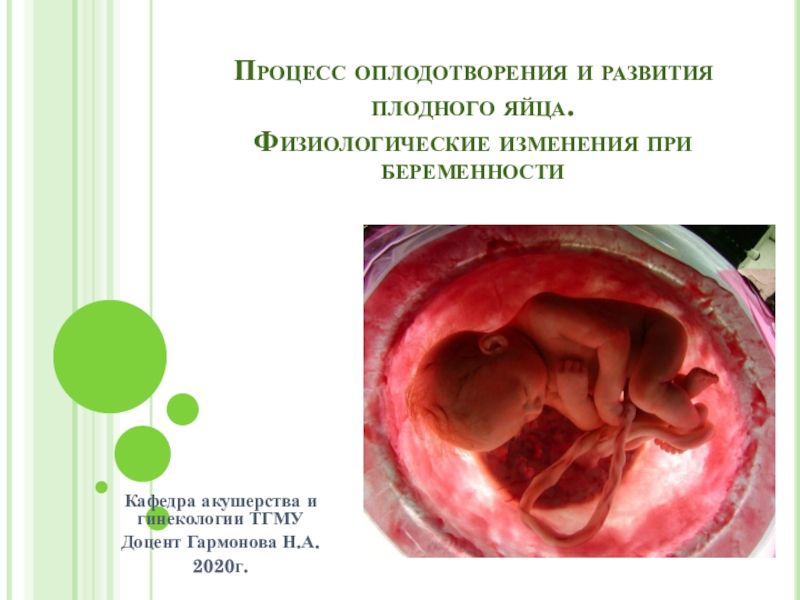
Слайд 24Файлы записей
Объявление указателя на файл:
var F: file of TBook;
Assign(F, 'books.dat');
{ связать с указателем }
Rewrite(F); { открыть
файл для запись }
writeln(F, Book); { запись }
for i:=1 to 5 do
writeln(aBook[i]); { запись }
Close(F); { закрыть файл }
Запись в файл:
Слайд 25Чтение из файла
Известное число записей:
Assign(F, 'books.dat'); { связать с указателем
}
Reset(F); { открыть для чтения }
Read(F, Book);
{ чтение }
for i:=1 to 5 do
Read(F, aBook[i]); { чтение }
Close(F); { закрыть файл }
«Пока не кончатся»:
count := 0;
while not eof(F) do begin
count := count + 1; { счетчик }
Read(F, aBook[count]); { чтение }
end;
пока не дошли до конца файла F
EOF = end of file
Слайд 26Пример программы
Задача: в файле books.dat записаны данные о книгах в
виде массива структур типа TBook (не более 100). Установить для
всех 2008 год издания и записать обратно в тот же файл.
type Tbook … ;
const MAX = 100;
var aBooks: array[1..MAX] of TBook;
i, N: integer;
F: file of TBook;
begin
{ прочитать записи из файла, N - количество }
for i:=1 to N do
aBooks[i].year := 2008;
{ сохранить в файле }
end.
type TBook … ;
полное описание структуры
Слайд 27Пример программы
Чтение «пока не кончатся»:
Assign(f, 'books.dat');
Reset(f);
N :=
0;
while not eof(F) and (N < MAX) do begin
N := N + 1;
read(F, aBooks[N]);
end;
Сlose(f);
Assign(f, 'books.dat'); { можно без этого }
Rewrite(f);
for i:=1 to N do write(F, aBooks[i]);
Close(f);
Сохранение:
чтобы не выйти за пределы массива
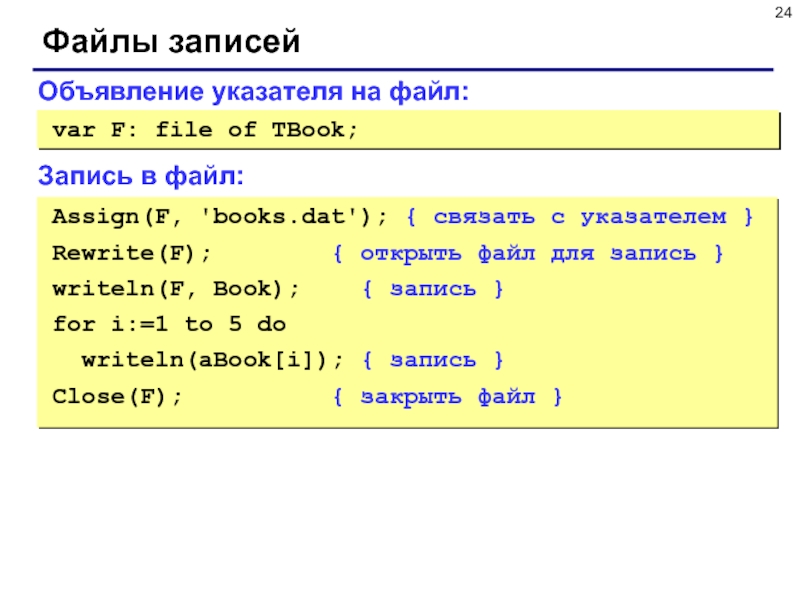
Слайд 28Выделение памяти под запись
var pB: ^TBook;
begin
New(pB);
pB^.author := 'А.С.
Пушкин';
pB^.title := 'Полтава';
pB^.year := 1990;
pB^.pages := 129;
Dispose(pB);
end.
New(pB);
выделить память под запись, записать адрес в pB
pB^
Dispose(pB);
освободить память
pB: ^TBook;
переменная-указатель на TBook
Слайд 29Сортировка массива записей
Ключ (ключевое поле) – это поле записи (или
комбинация полей), по которому выполняется сортировка.
const N = 100;
var aBooks:
array[1..N] of TBook;
i, j, N: integer;
temp: TBook; { для обмена }
begin
{ заполнить массив aBooks }
{ отсортировать = переставить }
for i:=1 to N do
writeln(aBooks[i].title,
aBooks[i].year:5);
end.
Слайд 30Сортировка массива записей
for i:=1 to N-1 do
for j:=N-1
downto i do
if aBooks[j].year > aBooks[j+1].year
then begin
temp := aBooks[j];
aBooks[j] := aBooks[j+1];
aBooks[j+1] := temp;
end;
Слайд 31Сортировка массива записей
Проблема:
как избежать копирования записи при сортировке?
Решение:
использовать
вспомогательный массив указателей, при сортировке переставлять указатели.
До
сортировки:
После
сортировки:
Вывод результата:
for i:=1
to N do
writeln(p[i]^.title, p[i]^.year:5);
p[i]^
p[i]^
Слайд 32Реализация в программе
type PBook = ^TBook; { новый тип данных
}
var p: array[1..N] of PBook;
begin
{ заполнение массива
записей}
for i:=1 to N do
p[i] := @aBooks[i];
for i:=1 to N do
writeln(p[i]^.title, p[i]^.year:5);
end.
for i:=1 to N-1 do
for j:=N-1 downto i do
if p[j]^.year > p[j+1]^.year then begin
temp := p[j];
p[j] := p[j+1];
p[j+1] := temp;
end;
вспомогательные указатели
меняем только указатели, записи остаются на местах
начальная расстановка
Слайд 33Тема 4. Списки
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
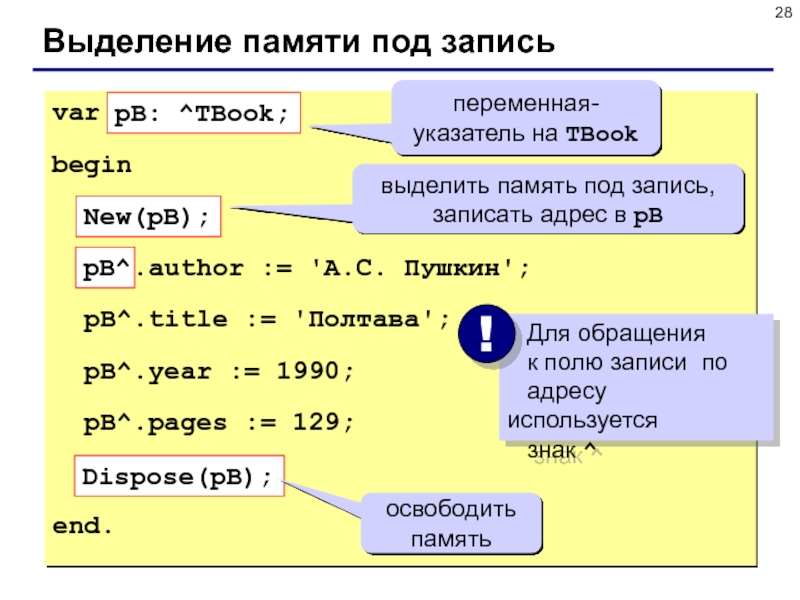
Слайд 34Динамические структуры данных
Строение: набор узлов, объединенных с помощью ссылок.
Как устроен
узел:
Типы структур:
списки
деревья
графы
односвязный
двунаправленный (двусвязный)
циклические списки (кольца)
Слайд 35Когда нужны списки?
Задача (алфавитно-частотный словарь). В файле записан текст.
Нужно записать в другой файл в столбик все
слова,
встречающиеся в тексте, в алфавитном порядке, и количество
повторений для каждого слова.
Проблемы:
количество слов заранее неизвестно (статический массив);
количество слов определяется только в конце работы (динамический массив).
Решение – список.
Алгоритм:
создать список;
если слова в файле закончились, то стоп.
прочитать слово и искать его в списке;
если слово найдено – увеличить счетчик повторений,
иначе добавить слово в список;
перейти к шагу 2.
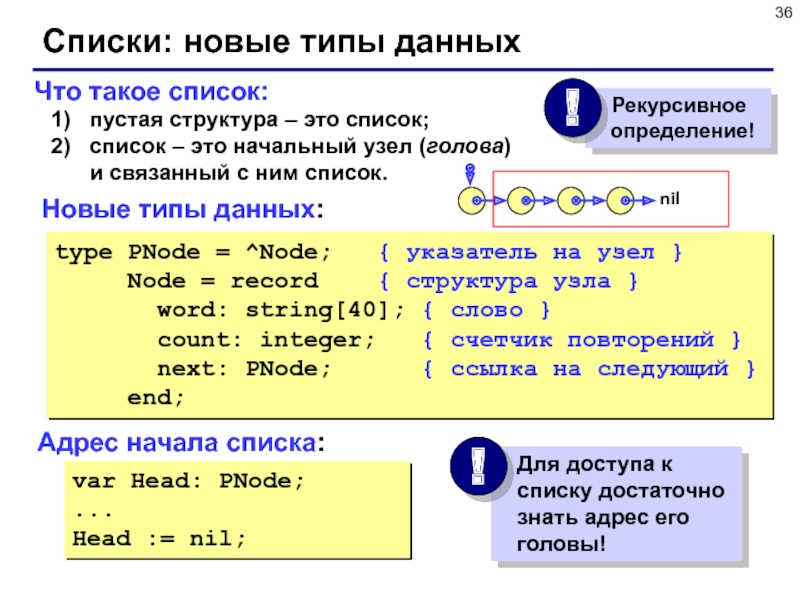
Слайд 36Что такое список:
пустая структура – это список;
список – это начальный
узел (голова)
и связанный с ним список.
Списки: новые типы данных
type
PNode = ^Node; { указатель на узел }
Node = record { структура узла }
word: string[40]; { слово }
count: integer; { счетчик повторений }
next: PNode; { ссылка на следующий }
end;
Новые типы данных:
Адрес начала списка:
var Head: PNode;
...
Head := nil;
Слайд 37Что нужно уметь делать со списком?
Создать новый узел.
Добавить узел:
а) в
начало списка;
б) в конец списка;
в) после заданного узла;
г) до заданного
узла.
Искать нужный узел в списке.
Удалить узел.
Слайд 38Создание узла
function CreateNode(NewWord: string): PNode;
var NewNode: PNode;
begin
New(NewNode);
NewNode^.word :=
NewWord;
NewNode^.count := 1;
NewNode^.next := nil;
Result := NewNode;
end;
Функция
CreateNode (создать узел):
вход: новое слово, прочитанное из файла;
выход: адрес нового узла, созданного в памяти.
возвращает адрес созданного узла
новое слово
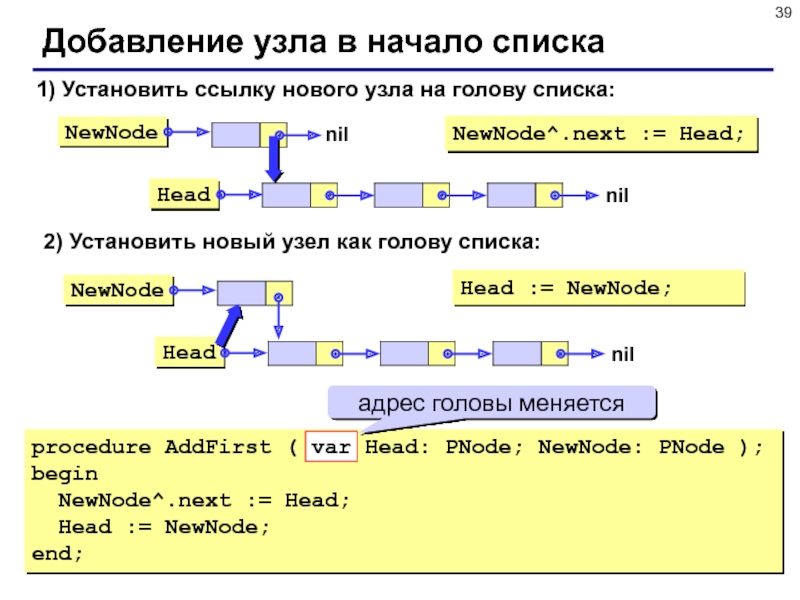
Слайд 39Добавление узла в начало списка
1) Установить ссылку нового узла на
голову списка:
NewNode^.next := Head;
2) Установить новый узел как голову списка:
Head
:= NewNode;
procedure AddFirst ( var Head: PNode; NewNode: PNode );
begin
NewNode^.next := Head;
Head := NewNode;
end;
var
адрес головы меняется
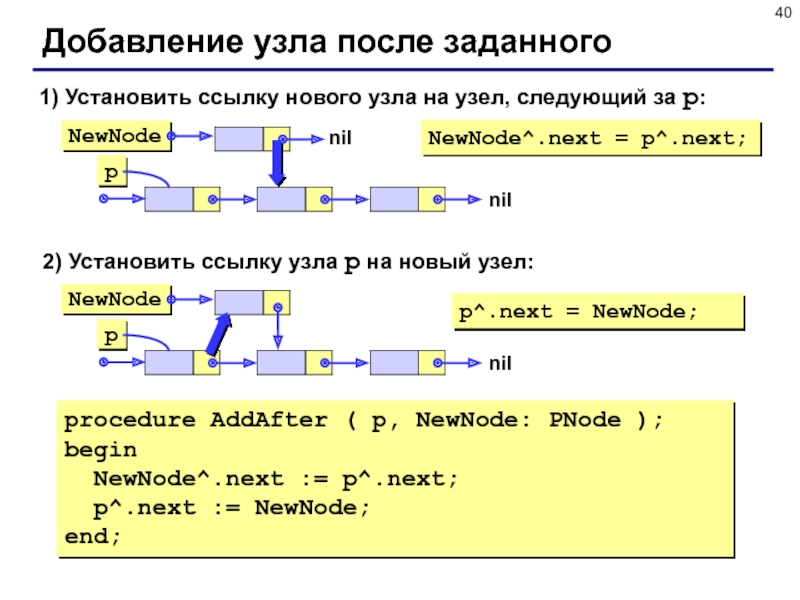
Слайд 40Добавление узла после заданного
1) Установить ссылку нового узла на узел,
следующий за p:
NewNode^.next = p^.next;
2) Установить ссылку узла p на
новый узел:
p^.next = NewNode;
procedure AddAfter ( p, NewNode: PNode );
begin
NewNode^.next := p^.next;
p^.next := NewNode;
end;
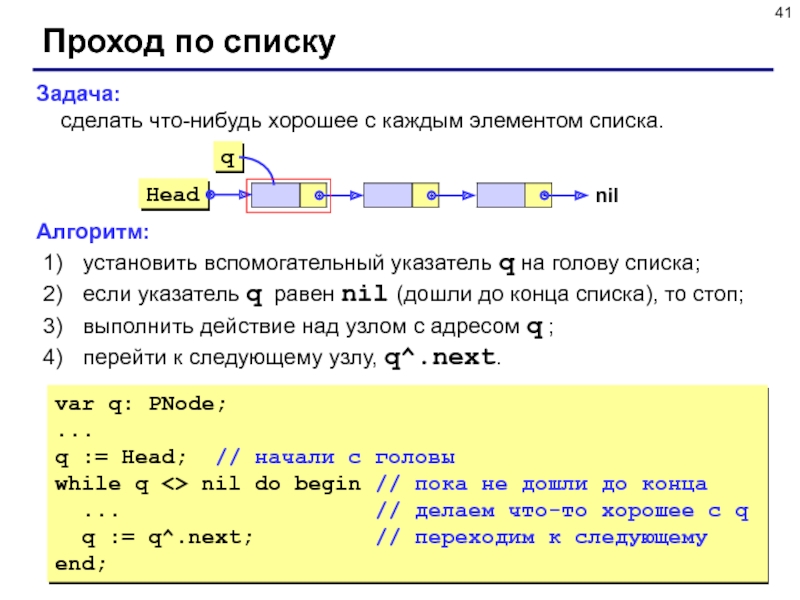
Слайд 41Задача:
сделать что-нибудь хорошее с каждым элементом списка.
Алгоритм:
установить вспомогательный
указатель q на голову списка;
если указатель q равен nil (дошли
до конца списка), то стоп;
выполнить действие над узлом с адресом q ;
перейти к следующему узлу, q^.next.
Проход по списку
var q: PNode;
...
q := Head; // начали с головы
while q <> nil do begin // пока не дошли до конца
... // делаем что-то хорошее с q
q := q^.next; // переходим к следующему
end;
Слайд 42Добавление узла в конец списка
Задача: добавить новый узел в конец
списка.
Алгоритм:
найти последний узел q, такой что q^.next равен nil;
добавить
узел после узла с адресом q (процедура AddAfter).
Особый случай: добавление в пустой список.
procedure AddLast ( var Head: PNode; NewNode: PNode );
var q: PNode;
begin
if Head = nil then
AddFirst ( Head, NewNode )
else begin
q := Head;
while q^.next <> nil do
q := q^.next;
AddAfter ( q, NewNode );
end;
end;
особый случай – добавление в пустой список
ищем последний узел
добавить узел после узла q
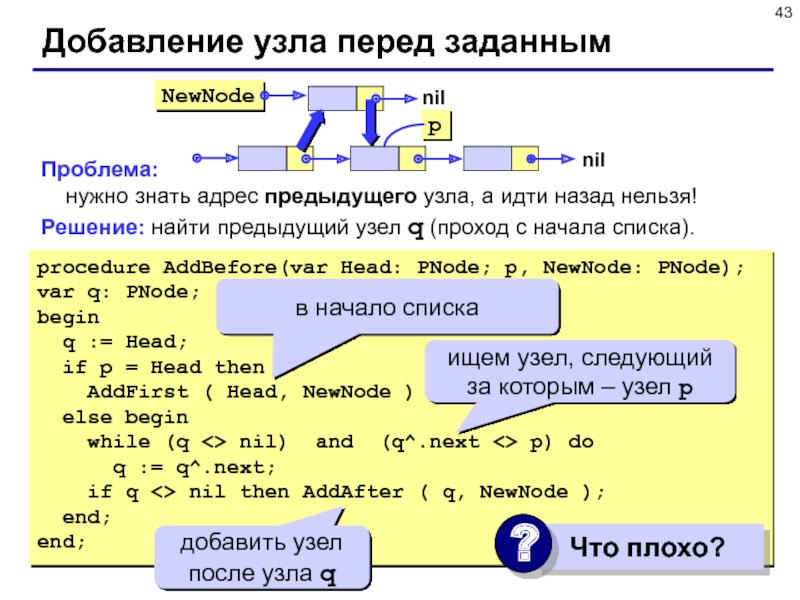
Слайд 43Проблема:
нужно знать адрес предыдущего узла, а идти
назад нельзя!
Решение: найти предыдущий узел q (проход с начала списка).
Добавление
узла перед заданным
procedure AddBefore(var Head: PNode; p, NewNode: PNode);
var q: PNode;
begin
q := Head;
if p = Head then
AddFirst ( Head, NewNode )
else begin
while (q <> nil) and (q^.next <> p) do
q := q^.next;
if q <> nil then AddAfter ( q, NewNode );
end;
end;
в начало списка
ищем узел, следующий за которым – узел p
добавить узел после узла q
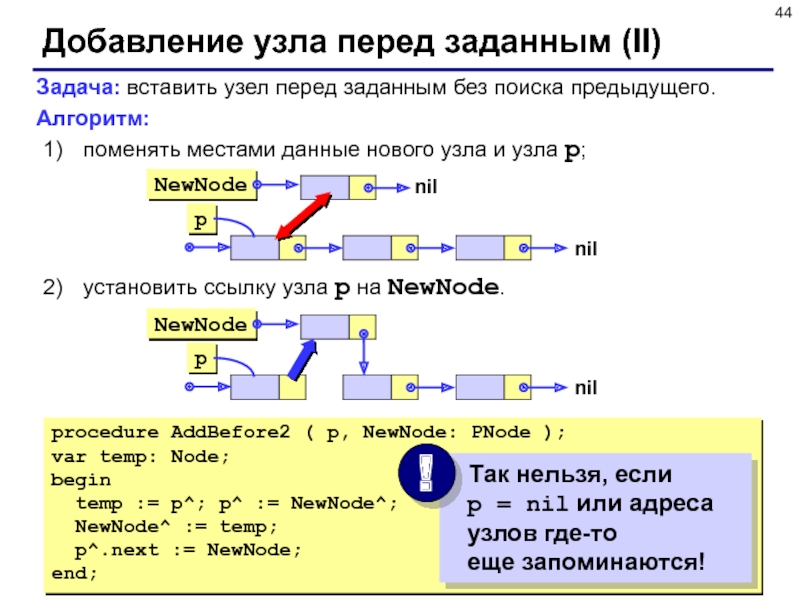
Слайд 44Добавление узла перед заданным (II)
Задача: вставить узел перед заданным без
поиска предыдущего.
Алгоритм:
поменять местами данные нового узла и узла p;
установить ссылку
узла p на NewNode.
procedure AddBefore2 ( p, NewNode: PNode );
var temp: Node;
begin
temp := p^; p^ := NewNode^;
NewNode^ := temp;
p^.next := NewNode;
end;
Слайд 45Поиск слова в списке
Задача:
найти в списке заданное слово или
определить, что его нет.
Функция Find:
вход: слово (символьная строка);
выход: адрес
узла, содержащего это слово или nil.
Алгоритм: проход по списку.
function Find(Head: PNode; NewWord: string): PNode;
var q: PNode;
begin
q := Head;
while (q <> nil) and (NewWord <> q^.word) do
q := q^.next;
Result := q;
end;
ищем это слово
результат – адрес узла или nil (нет такого)
while (q <> nil) and (NewWord <> q^.word) do
q := q^.next;
пока не дошли до конца списка
и слово не равно заданному
Слайд 46Куда вставить новое слово?
Задача:
найти узел, перед которым нужно вставить,
заданное слово, так чтобы в списке сохранился алфавитный порядок слов.
Функция FindPlace:
вход: слово (символьная строка);
выход: адрес узла, перед которым нужно вставить это слово или
nil, если слово нужно вставить в конец списка.
function FindPlace(Head: PNode; NewWord: string): PNode;
var q: PNode;
begin
q := Head;
while (q <> nil) and (NewWord > q^.word) do
q := q^.next;
Result := q;
end;
>
слово NewWord стоит по алфавиту перед q^.word
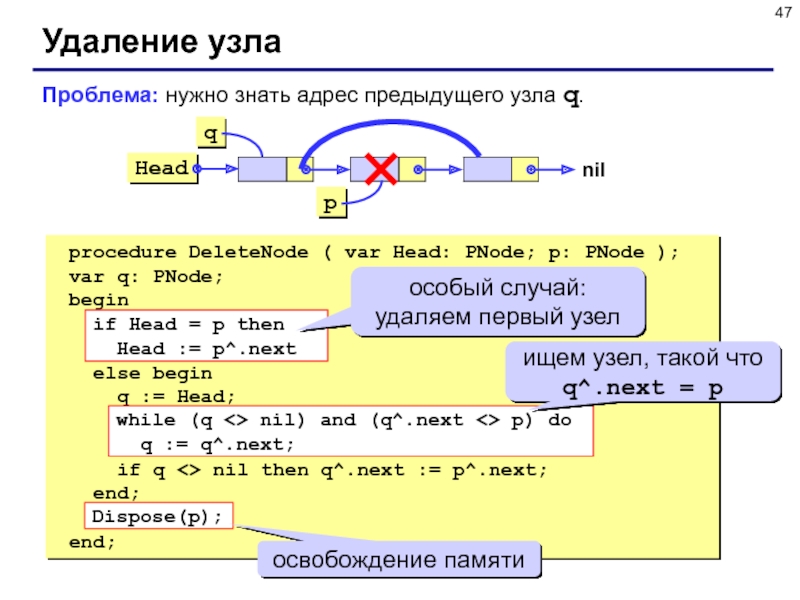
Слайд 47Удаление узла
procedure DeleteNode ( var Head: PNode; p: PNode );
var
q: PNode;
begin
if Head = p then
Head :=
p^.next
else begin
q := Head;
while (q <> nil) and (q^.next <> p) do
q := q^.next;
if q <> nil then q^.next := p^.next;
end;
Dispose(p);
end;
while (q <> nil) and (q^.next <> p) do
q := q^.next;
if Head = p then
Head := p^.next
Проблема: нужно знать адрес предыдущего узла q.
особый случай: удаляем первый узел
ищем узел, такой что
q^.next = p
Dispose(p);
освобождение памяти
Слайд 48Алфавитно-частотный словарь
Алгоритм:
открыть файл на чтение;
прочитать очередное слово (как?)
если файл закончился,
то перейти к шагу 7;
если слово найдено, увеличить счетчик (поле
count);
если слова нет в списке, то
создать новый узел, заполнить поля (CreateNode);
найти узел, перед которым нужно вставить слово (FindPlace);
добавить узел (AddBefore);
перейти к шагу 2;
закрыть файл
вывести список слов, используя проход по списку.
var F: Text;
...
Assign(F, 'input.dat');
Reset ( F );
Close ( F );
Слайд 49Как прочитать одно слово из файла?
function GetWord ( F: Text
) : string;
var c: char;
begin
Result := ''; { пустая
строка }
c := ' '; { пробел – чтобы войти в цикл }
{ пропускаем спецсимволы и пробелы }
while not eof(f) and (c <= ' ') do
read(F, c);
{ читаем слово }
while not eof(f) and (c > ' ') do begin
Result := Result + c;
read(F, c);
end;
end;
Алгоритм:
пропускаем все спецсимволы и пробелы (с кодами <= 32)
читаем все символы до первого пробела или спецсимвола
Слайд 50Полная программа
type PNode = ^Node;
Node = record
... end; { новые типы данных }
var Head: PNode;
{ адрес головы списка }
NewNode, q: PNode; { вспомогательные указатели }
w: string; { слово из файла }
F: text; { файловая переменная }
count: integer; { счетчик разных слов }
{ процедуры и функции }
begin
Head := nil;
Assign ( F, 'input.txt' );
Reset ( F );
{ читаем слова из файла, строим список }
Close ( F );
{ выводим список в другой файл }
end.
Слайд 51Полная программа (II)
{ читаем слова из файла, строим список }
while
True do begin { бесконечный цикл }
w
:= GetWord ( F ); { читаем слово }
if w = '' then break; { слова закончились, выход }
q := Find ( Head, w ); { ищем слово в списке }
if q <> nil then { нашли, увеличить счетчик }
q^.count := q^.count + 1
else begin { не нашли, добавить в список }
NewNode := CreateNode ( w );
q := FindPlace ( Head, w );
AddBefore ( Head, q, NewNode );
end;
end;
Слайд 52Полная программа (III)
{ выводим список в другой файл }
q :=
Head; { проход с начала списка }
count
:= 0; { обнулили счетчик слов }
Assign(F, 'output.txt');
Rewrite(F);
while q <> nil do begin { пока не конец списка }
count := count + 1; { еще одно слово }
writeln ( F, q^.word, ': ', q^.count );
q := q^.next; { перейти к следующему }
end;
writeln ( F, 'Найдено ',
count, ' разных слов.' );
Close(F);
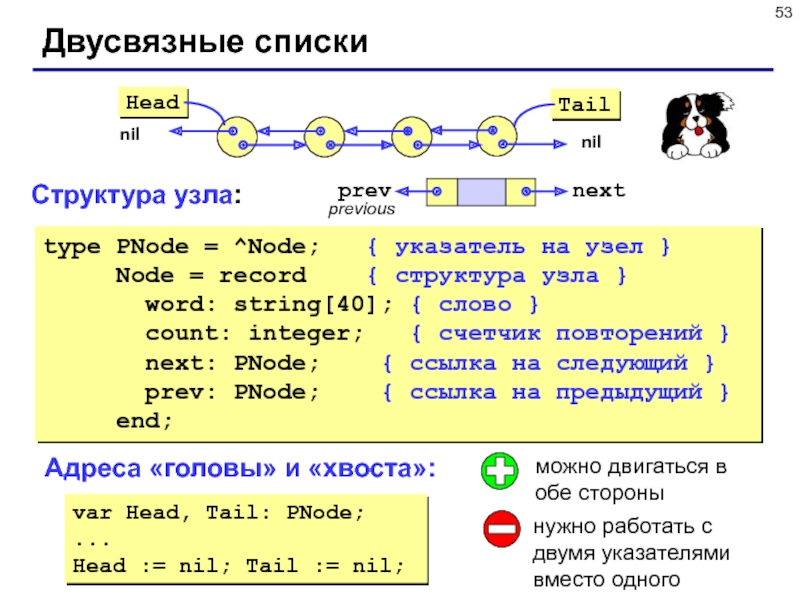
Слайд 53type PNode = ^Node; { указатель на узел }
Node = record { структура
узла }
word: string[40]; { слово }
count: integer; { счетчик повторений }
next: PNode; { ссылка на следующий }
prev: PNode; { ссылка на предыдущий }
end;
Двусвязные списки
Структура узла:
Адреса «головы» и «хвоста»:
var Head, Tail: PNode;
...
Head := nil; Tail := nil;
Слайд 54Задания
«4»: «Собрать» из этих функций программу для построения алфавитно-частотного словаря.
В конце файла вывести общее количество разных слов (количество элементов
списка).
«5»: То же самое, но использовать двусвязные списки.
«6»: То же самое, что и на «5», но вывести список слов в порядке убывания частоты, то есть, сначала те слова, которые встречаются чаще всего.
Слайд 55Тема 5. Стеки, очереди, деки
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык
Паскаль)
Слайд 56Стек
Стек – это линейная структура данных, в которой добавление и
удаление элементов возможно только с одного конца (вершины стека). Stack
= кипа, куча, стопка (англ.)
LIFO = Last In – First Out
«Кто последним вошел, тот первым вышел».
Операции со стеком:
добавить элемент на вершину
(Push = втолкнуть);
снять элемент с вершины
(Pop = вылететь со звуком).
Слайд 57Пример задачи
Задача: вводится символьная строка, в которой записано выражение со
скобками трех типов: [], {} и (). Определить, верно ли
расставлены скобки (не обращая внимания на остальные символы). Примеры:
[()]{} ][ [({)]}
Упрощенная задача: то же самое, но с одним видом скобок.
Решение: счетчик вложенности скобок. Последовательность правильная, если в конце счетчик равен нулю и при проходе не разу не становился отрицательным.
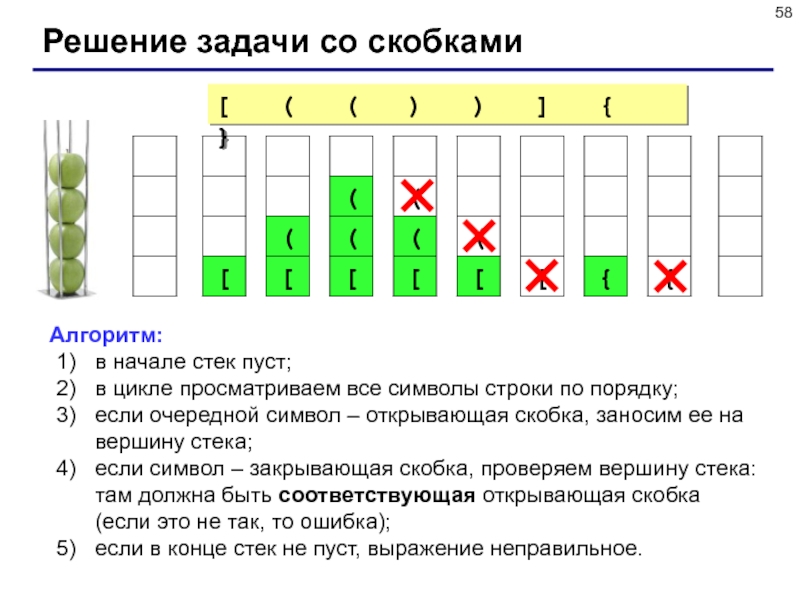
Слайд 58Решение задачи со скобками
Алгоритм:
в начале стек пуст;
в цикле просматриваем все
символы строки по порядку;
если очередной символ – открывающая скобка, заносим
ее на вершину стека;
если символ – закрывающая скобка, проверяем вершину стека: там должна быть соответствующая открывающая скобка (если это не так, то ошибка);
если в конце стек не пуст, выражение неправильное.
[ ( ( ) ) ] { }
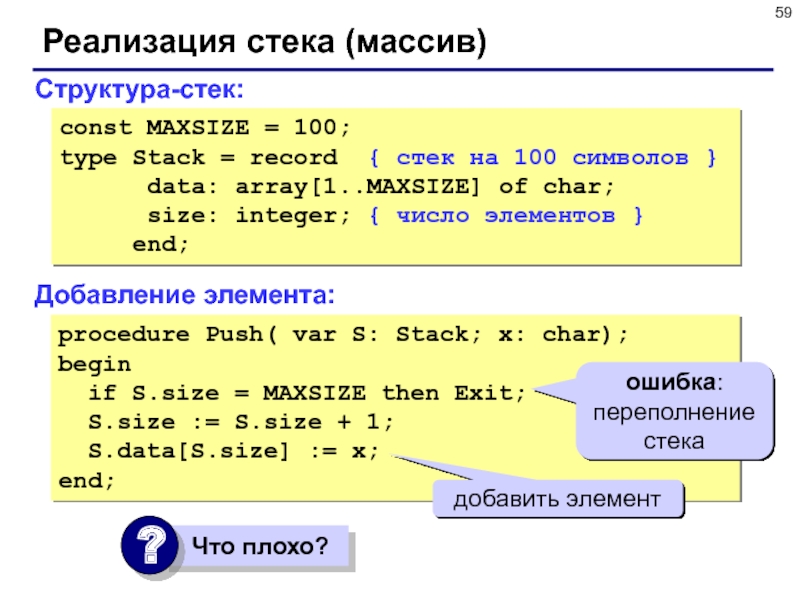
Слайд 59Реализация стека (массив)
Структура-стек:
const MAXSIZE = 100;
type Stack = record {
стек на 100 символов }
data: array[1..MAXSIZE] of
char;
size: integer; { число элементов }
end;
Добавление элемента:
procedure Push( var S: Stack; x: char);
begin
if S.size = MAXSIZE then Exit;
S.size := S.size + 1;
S.data[S.size] := x;
end;
ошибка: переполнение стека
добавить элемент
Слайд 60Реализация стека (массив)
function Pop ( var S:Stack ): char;
begin
if
S.size = 0 then begin
Result := char(255);
Exit;
end;
Result := S.data[S.size];
S.size := S.size - 1;
end;
Снятие элемента с вершины:
Пустой или нет?
function isEmpty ( S: Stack ): Boolean;
begin
Result := (S.size = 0);
end;
ошибка:
стек пуст
Слайд 61Программа
var br1, br2, expr: string;
i, k: integer;
upper: char; { то, что сняли со стека }
error: Boolean; { признак ошибки }
S: Stack;
begin
br1 := '([{'; br2 := ')]}';
S.size := 0;
error := False;
writeln('Введите выражение со скобками');
readln(expr);
... { здесь будет основной цикл обработки }
if not error and isEmpty(S) then
writeln('Выражение правильное.')
else writeln('Выражение неправильное.')
end.
открывающие скобки
закрывающие скобки
Слайд 62Обработка строки (основной цикл)
for i:=1 to length(expr)
do
begin
for k:=1 to 3 do begin
if expr[i] = br1[k] then begin { откр. скобка }
Push(S, expr[i]); { втолкнуть в стек}
break;
end;
if expr[i] = br2[k] then begin { закр. скобка }
upper := Pop(S); { снять символ со стека }
error := upper <> br1[k];
break;
end;
end;
if error then break;
end;
цикл по всем символам строки expr
цикл по всем видам скобок
ошибка: стек пуст или не та скобка
была ошибка: дальше нет смысла проверять
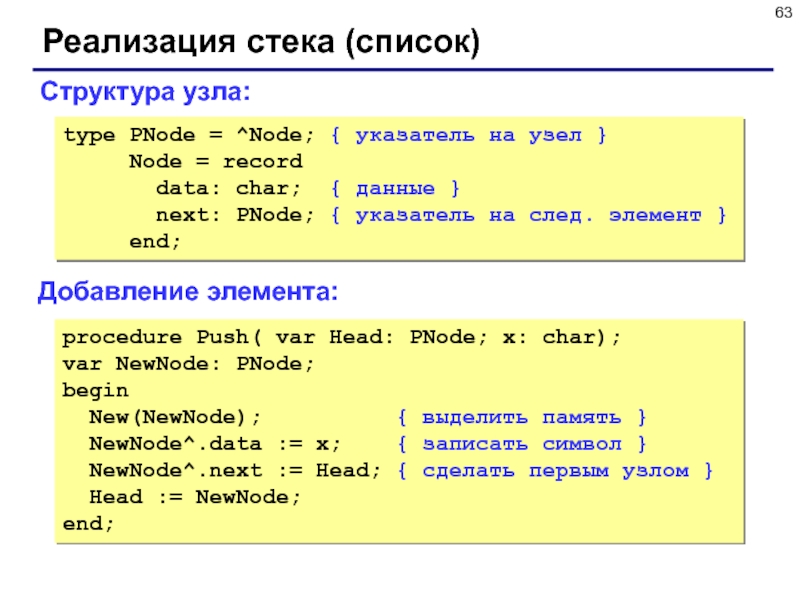
Слайд 63Реализация стека (список)
Добавление элемента:
Структура узла:
type PNode = ^Node; { указатель
на узел }
Node = record
data: char; { данные }
next: PNode; { указатель на след. элемент }
end;
procedure Push( var Head: PNode; x: char);
var NewNode: PNode;
begin
New(NewNode); { выделить память }
NewNode^.data := x; { записать символ }
NewNode^.next := Head; { сделать первым узлом }
Head := NewNode;
end;
Слайд 64Реализация стека (список)
Снятие элемента с вершины:
function Pop ( var Head:
PNode ): char;
var q: PNode;
begin
if Head = nil then
begin { стек пуст }
Result := char(255); { неиспользуемый символ }
Exit;
end;
Result := Head^.data; { взять верхний символ }
q := Head; { запомнить вершину }
Head := Head^.next; { удалить вершину из стека }
Dispose(q); { удалить из памяти }
end;
q := Head;
Head := Head^.next;
Dispose(q);
Слайд 65Реализация стека (список)
Изменения в основной программе:
var S: Stack;
...
S.size := 0;
var
S: PNode;
S := nil;
Пустой или нет?
function isEmpty ( S: Stack
): Boolean;
begin
Result := (S = nil);
end;
Слайд 66Вычисление арифметических выражений
a b + c d + 1 -
/
Как вычислять автоматически:
Инфиксная запись
(знак операции между операндами)
(a + b) /
(c + d – 1)
необходимы скобки!
Постфиксная запись (знак операции после операндов)
польская нотация,
Jan Łukasiewicz (1920)
скобки не нужны, можно однозначно вычислить!
Префиксная запись (знак операции до операндов)
/ + a b - + c d 1
обратная польская нотация,
F. L. Bauer and E. W. Dijkstra
a + b
a + b
c + d
c + d
c + d - 1
c + d - 1
Слайд 67Запишите в постфиксной форме
(32*6-5)*(2*3+4)/(3+7*2)
(2*4+3*5)*(2*3+18/3*2)*(12-3)
(4-2*3)*(3-12/3/4)*(24-3*12)
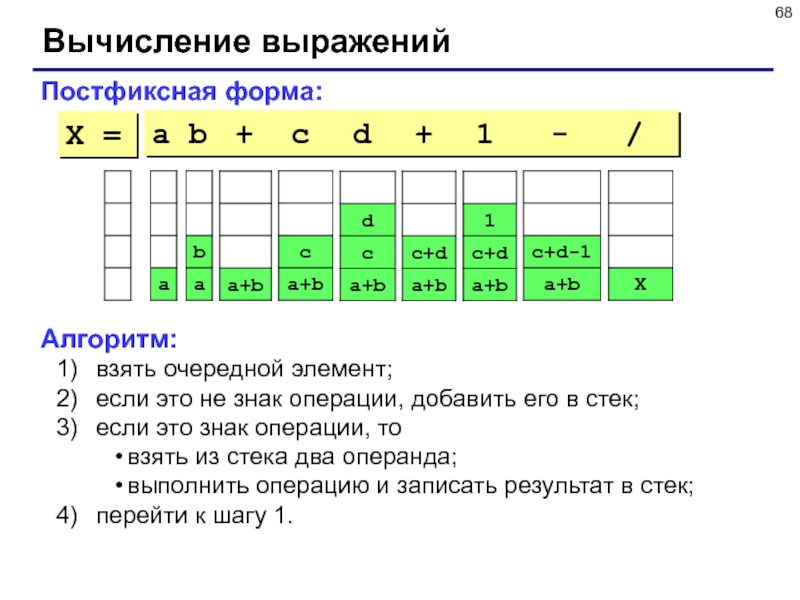
Слайд 68Вычисление выражений
Постфиксная форма:
a b + c d +
1 - /
Алгоритм:
взять очередной элемент;
если это
не знак операции, добавить его в стек;
если это знак операции, то
взять из стека два операнда;
выполнить операцию и записать результат в стек;
перейти к шагу 1.
X =
Слайд 69Системный стек (Windows – 1 Мб)
Используется для
размещения локальных переменных;
хранения
адресов возврата (по которым переходит программа после выполнения функции или
процедуры);
передачи параметров в функции и процедуры;
временного хранения данных (в программах на языке Ассмеблер).
Переполнение стека (stack overflow):
слишком много локальных переменных
(выход – использовать динамические массивы);
очень много рекурсивных вызовов функций и процедур
(выход – переделать алгоритм так, чтобы уменьшить глубину рекурсии или отказаться от нее вообще).
Слайд 70Очередь
Очередь – это линейная структура данных, в которой
добавление элементов
возможно только с одного конца
(конца очереди), а удаление элементов
– только с другого конца (начала очереди).
FIFO = First In – First Out
«Кто первым вошел, тот первым вышел».
Операции с очередью:
добавить элемент в конец очереди (PushTail = втолкнуть
в конец);
удалить элемент с начала очереди (Pop).
Слайд 71Реализация очереди (массив)
самый простой способ
нужно заранее выделить массив;
при выборке из
очереди нужно сдвигать все элементы.
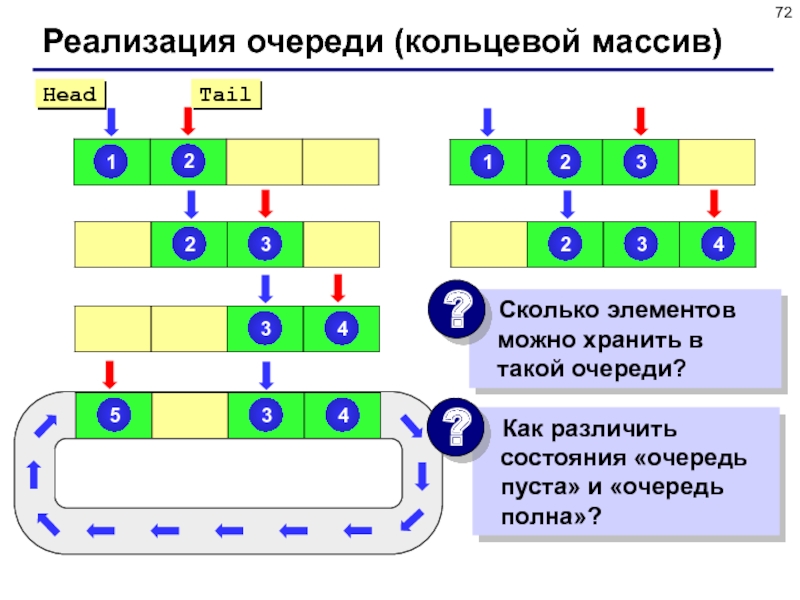
Слайд 72Реализация очереди (кольцевой массив)
Слайд 73Реализация очереди (кольцевой массив)
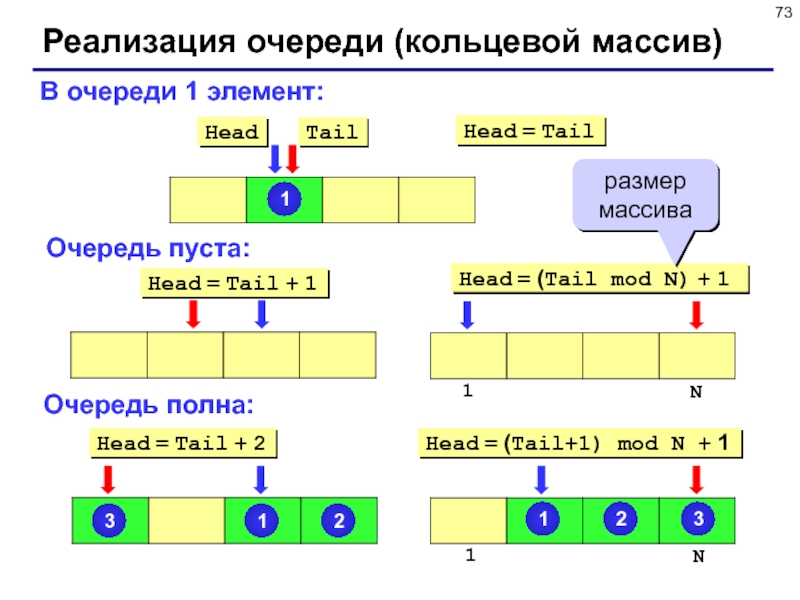
В очереди 1 элемент:
Очередь пуста:
Очередь полна:
Head =
Tail + 1
размер массива
Head = Tail + 2
Head = Tail
Слайд 74Реализация очереди (кольцевой массив)
type Queue = record
data: array[1..MAXSIZE] of integer;
head, tail: integer;
end;
Структура данных:
Добавление в очередь:
procedure PushTail( var Q: Queue; x: integer);
begin
if Q.head = (Q.tail+1) mod MAXSIZE + 1
then Exit; { очередь полна, не добавить }
Q.tail := Q.tail mod MAXSIZE + 1;
Q.data[Q.tail] := x;
end;
замкнуть в кольцо
mod MAXSIZE
Слайд 75Реализация очереди (кольцевой массив)
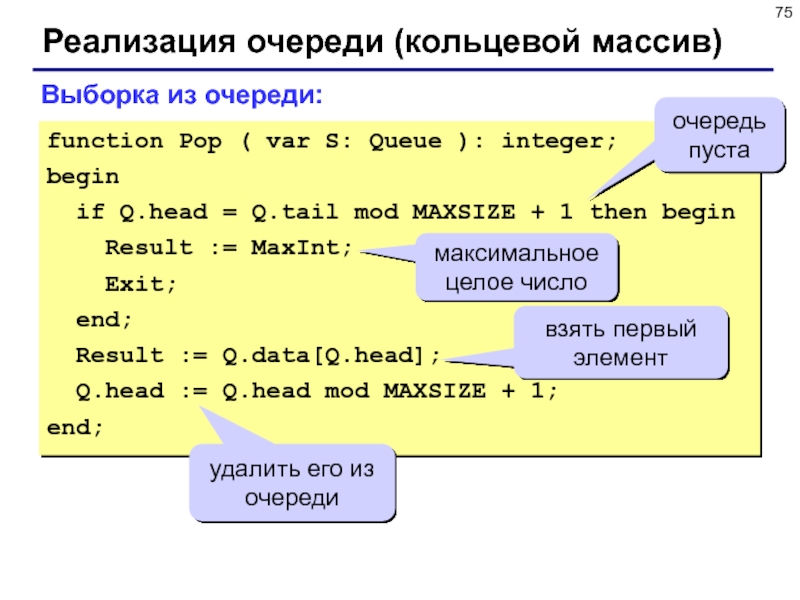
Выборка из очереди:
function Pop ( var S:
Queue ): integer;
begin
if Q.head = Q.tail mod MAXSIZE +
1 then begin
Result := MaxInt;
Exit;
end;
Result := Q.data[Q.head];
Q.head := Q.head mod MAXSIZE + 1;
end;
очередь пуста
взять первый элемент
удалить его из очереди
максимальное целое число
Слайд 76Реализация очереди (списки)
type PNode = ^Node;
Node =
record
data: integer;
next:
PNode;
end;
type Queue = record
head, tail: PNode;
end;
Структура узла:
Тип данных «очередь»:
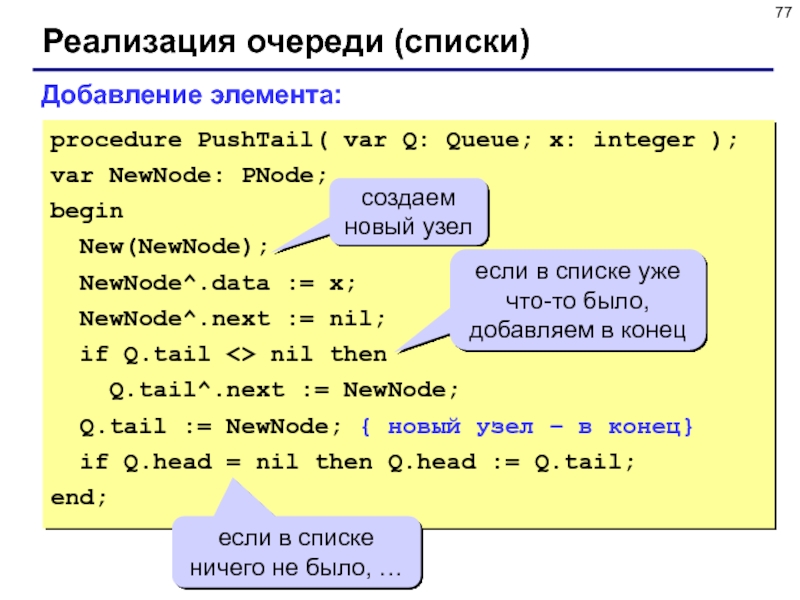
Слайд 77Реализация очереди (списки)
procedure PushTail( var Q: Queue; x: integer );
var
NewNode: PNode;
begin
New(NewNode);
NewNode^.data := x;
NewNode^.next := nil;
if
Q.tail <> nil then
Q.tail^.next := NewNode;
Q.tail := NewNode; { новый узел – в конец}
if Q.head = nil then Q.head := Q.tail;
end;
Добавление элемента:
создаем новый узел
если в списке уже что-то было, добавляем в конец
если в списке ничего не было, …
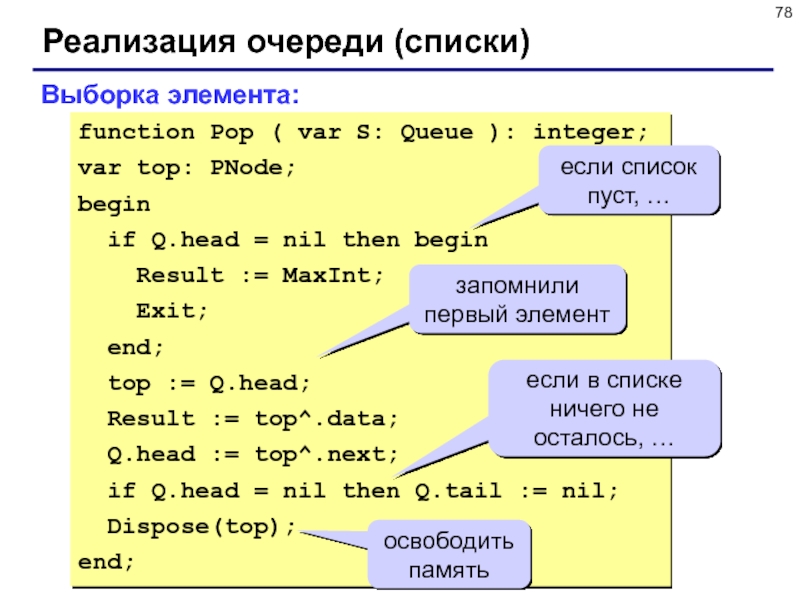
Слайд 78Реализация очереди (списки)
function Pop ( var S: Queue ): integer;
var
top: PNode;
begin
if Q.head = nil then begin
Result
:= MaxInt;
Exit;
end;
top := Q.head;
Result := top^.data;
Q.head := top^.next;
if Q.head = nil then Q.tail := nil;
Dispose(top);
end;
Выборка элемента:
если список пуст, …
запомнили первый элемент
если в списке ничего не осталось, …
освободить память
Слайд 79Дек
Дек (deque = double ended queue, очередь с двумя концами)
– это линейная структура данных, в которой добавление и удаление
элементов возможно с обоих концов.
Операции с деком:
добавление элемента в начало (Push);
удаление элемента с начала (Pop);
добавление элемента в конец (PushTail);
удаление элемента с конца (PopTail).
Реализация:
кольцевой массив;
двусвязный список.
Слайд 80Задания
«4»: В файле input.dat находится список чисел (или слов). Переписать
его в файл output.dat в обратном порядке.
«5»: Составить программу, которая
вычисляет значение арифметического выражения, записанного в постфиксной форме, с помощью стека. Выражение правильное, допускаются только однозначные числа и знаки +, -, *, /.
«6»: То же самое, что и на «5», но допускаются многозначные числа.
Слайд 81Тема 6. Деревья
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
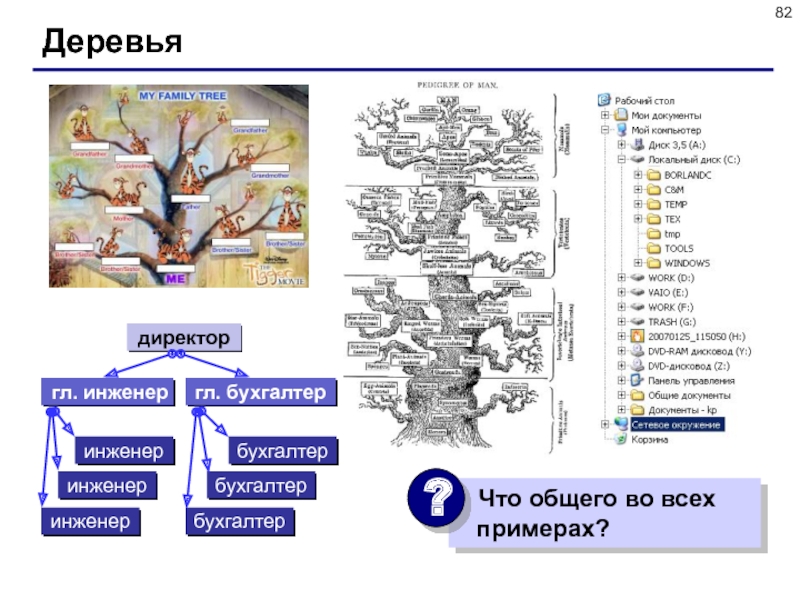
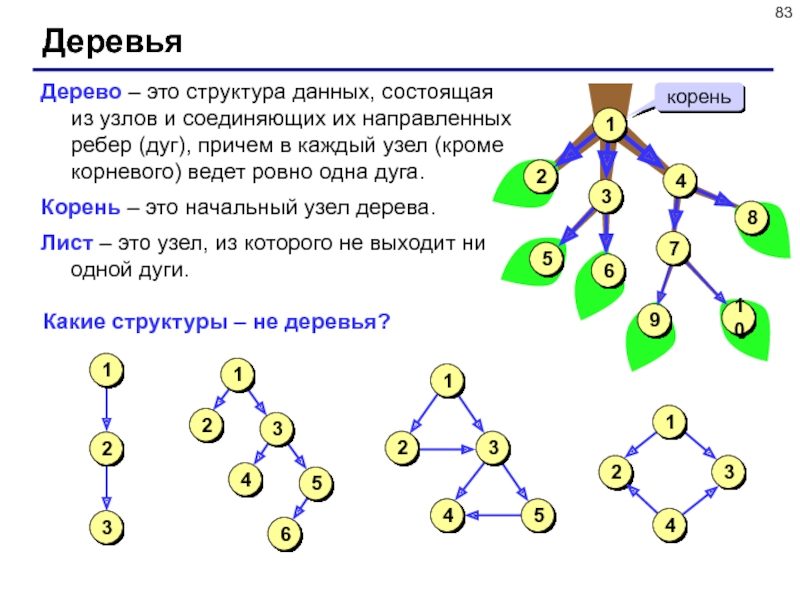
Слайд 83Деревья
Дерево – это структура данных, состоящая из узлов и соединяющих
их направленных ребер (дуг), причем в каждый узел (кроме корневого)
ведет ровно одна дуга.
Корень – это начальный узел дерева.
Лист – это узел, из которого не выходит ни одной дуги.
корень
Какие структуры – не деревья?
Слайд 84Деревья
Предок узла x – это узел, из которого существует путь
по стрелкам в узел x.
Потомок узла x – это узел,
в который существует путь по стрелкам из узла x.
Родитель узла x – это узел, из которого существует дуга непосредственно в узел x.
Сын узла x – это узел, в который существует дуга непосредственно из узла x.
Брат узла x (sibling) – это узел, у которого тот же родитель, что и у узла x.
Высота дерева – это наибольшее расстояние от корня до листа (количество дуг).
Слайд 85Дерево – рекурсивная структура данных
Рекурсивное определение:
Пустая структура – это дерево.
Дерево
– это корень и несколько связанных с ним деревьев.
Двоичное (бинарное)
дерево – это дерево, в котором каждый узел имеет не более двух сыновей.
Пустая структура – это двоичное дерево.
Двоичное дерево – это корень и два связанных с ним двоичных дерева (левое и правое поддеревья).
Слайд 86Двоичные деревья
Структура узла:
type PNode = ^Node; {
указатель на узел }
Node = record
data: integer; { полезные данные }
left, right: PNode; { ссылки на левого и
правого сыновей }
end;
Применение:
поиск данных в специально построенных деревьях
(базы данных);
сортировка данных;
вычисление арифметических выражений;
кодирование (метод Хаффмана).
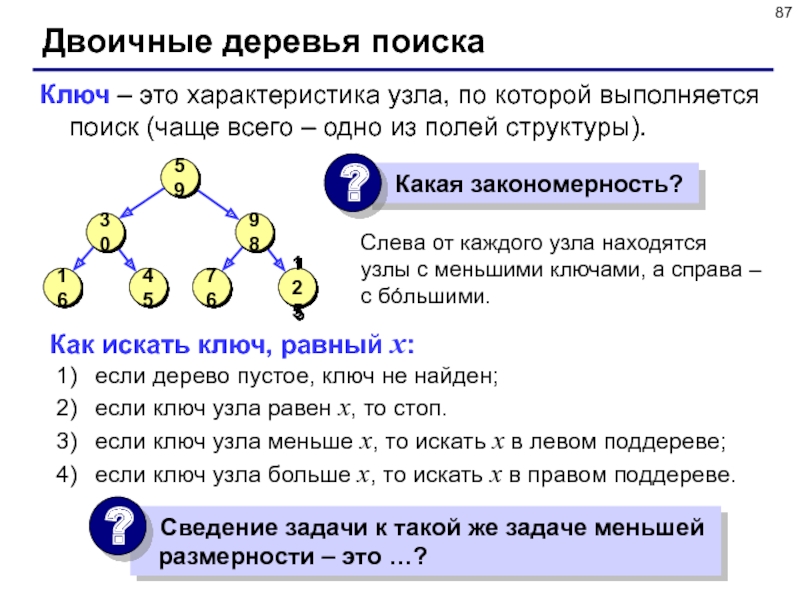
Слайд 87Двоичные деревья поиска
Слева от каждого узла находятся узлы с меньшими
ключами, а справа – с бóльшими.
Ключ – это характеристика узла,
по которой выполняется поиск (чаще всего – одно из полей структуры).
Как искать ключ, равный x:
если дерево пустое, ключ не найден;
если ключ узла равен x, то стоп.
если ключ узла меньше x, то искать x в левом поддереве;
если ключ узла больше x, то искать x в правом поддереве.
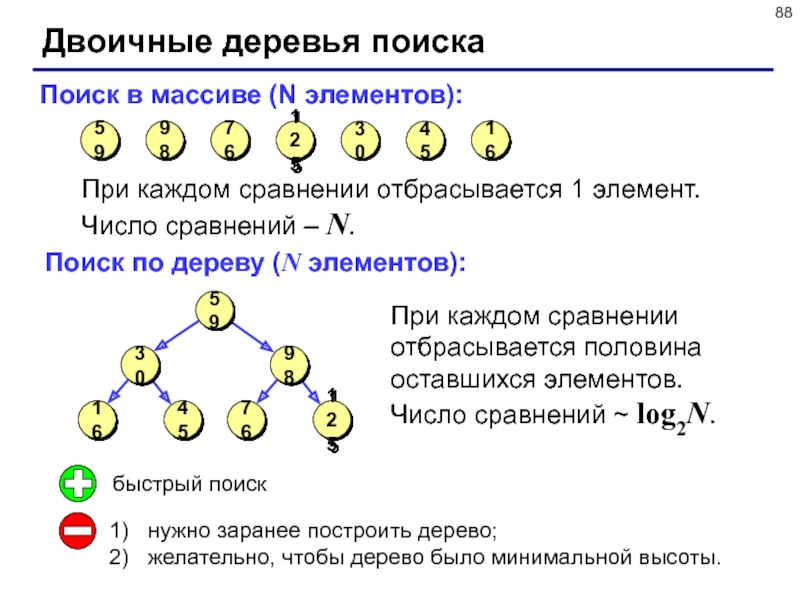
Слайд 88Двоичные деревья поиска
Поиск в массиве (N элементов):
При каждом сравнении отбрасывается
1 элемент.
Число сравнений – N.
Поиск по дереву (N элементов):
При каждом
сравнении отбрасывается половина оставшихся элементов.
Число сравнений ~ log2N.
быстрый поиск
нужно заранее построить дерево;
желательно, чтобы дерево было минимальной высоты.
Слайд 89Реализация алгоритма поиска
{ Функция Search – поиск по дереву
Вход:
Tree - адрес корня,
x - что ищем
Выход: адрес узла или nil (не нашли) }
function Search(Tree: PNode; x: integer): PNode;
begin
if Tree = nil then begin
Result := nil;
Exit;
end;
if x = Tree^.data then
Result := Tree
else
if x < Tree^.data then
Result := Search(Tree^.left, x)
else Result := Search(Tree^.right, x);
end;
дерево пустое: ключ не нашли…
нашли, возвращаем адрес корня
искать в левом поддереве
искать в правом поддереве
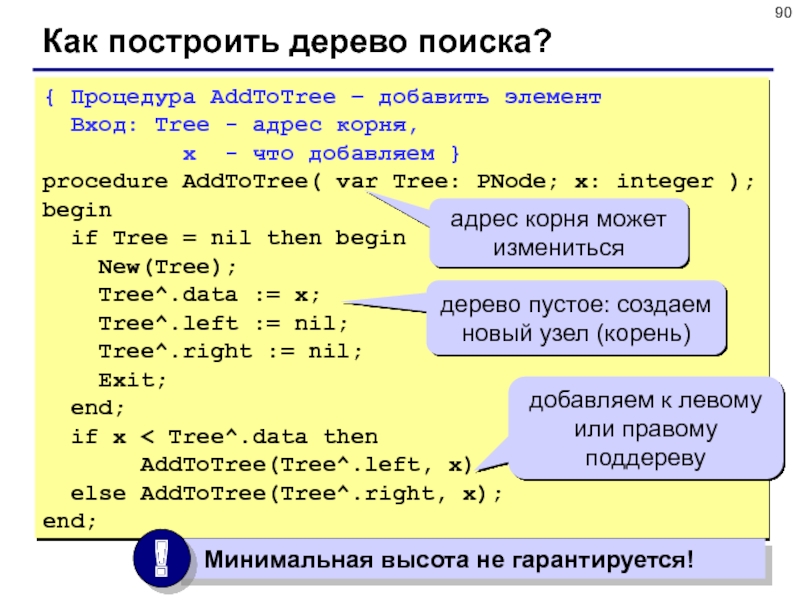
Слайд 90Как построить дерево поиска?
{ Процедура AddToTree – добавить элемент
Вход:
Tree - адрес корня,
x
- что добавляем }
procedure AddToTree( var Tree: PNode; x: integer );
begin
if Tree = nil then begin
New(Tree);
Tree^.data := x;
Tree^.left := nil;
Tree^.right := nil;
Exit;
end;
if x < Tree^.data then
AddToTree(Tree^.left, x)
else AddToTree(Tree^.right, x);
end;
дерево пустое: создаем новый узел (корень)
адрес корня может измениться
добавляем к левому или правому поддереву
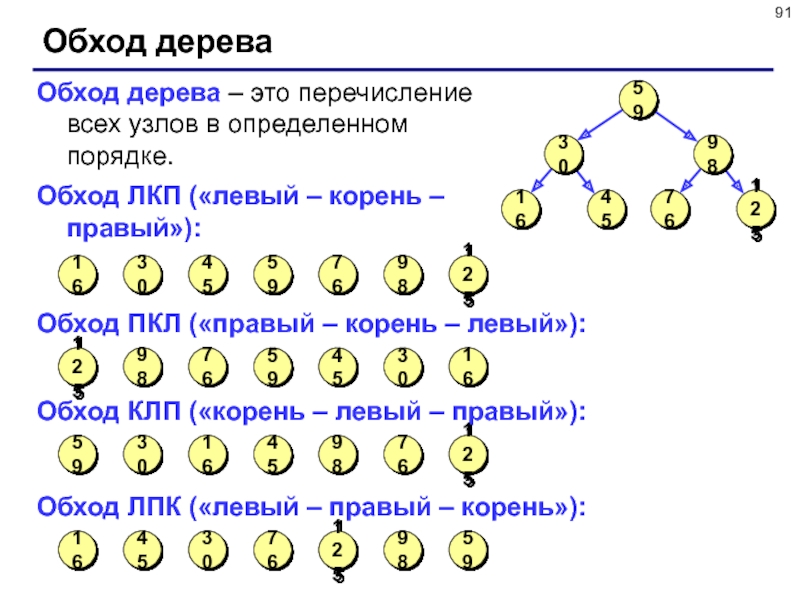
Слайд 91Обход дерева
Обход дерева – это перечисление всех узлов в определенном
порядке.
Обход ЛКП («левый – корень – правый»):
125
98
76
45
59
30
16
Обход ПКЛ («правый –
корень – левый»):
Обход КЛП («корень – левый – правый»):
Обход ЛПК («левый – правый – корень»):
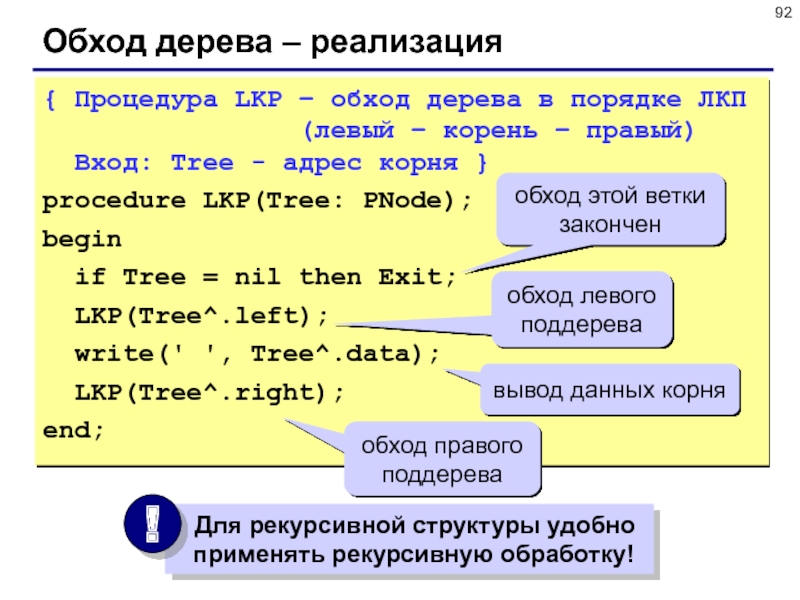
Слайд 92Обход дерева – реализация
{ Процедура LKP – обход дерева в
порядке ЛКП
(левый
– корень – правый)
Вход: Tree - адрес корня }
procedure LKP(Tree: PNode);
begin
if Tree = nil then Exit;
LKP(Tree^.left);
write(' ', Tree^.data);
LKP(Tree^.right);
end;
обход этой ветки закончен
обход левого поддерева
вывод данных корня
обход правого поддерева
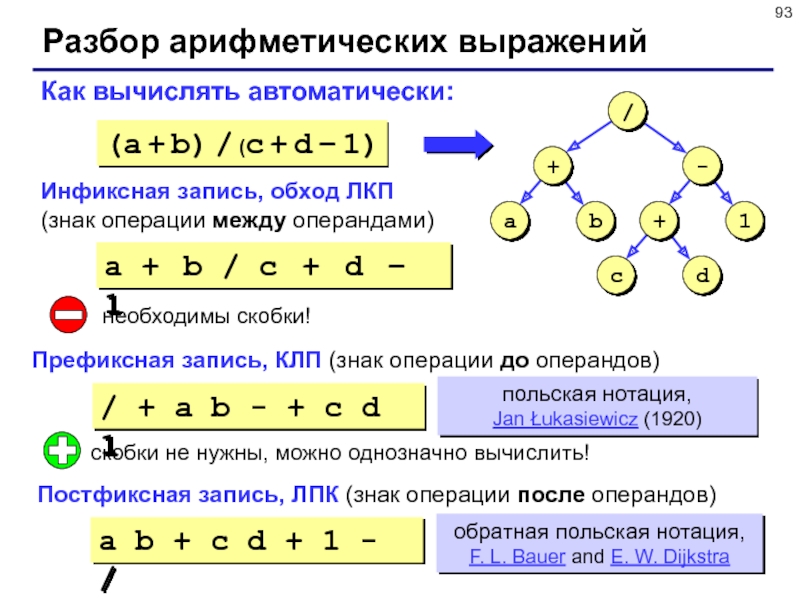
Слайд 93Разбор арифметических выражений
a b + c d + 1 -
/
Как вычислять автоматически:
Инфиксная запись, обход ЛКП
(знак операции между операндами)
(a +
b) / (c + d – 1)
необходимы скобки!
Постфиксная запись, ЛПК (знак операции после операндов)
a + b / c + d – 1
польская нотация,
Jan Łukasiewicz (1920)
скобки не нужны, можно однозначно вычислить!
Префиксная запись, КЛП (знак операции до операндов)
/ + a b - + c d 1
обратная польская нотация,
F. L. Bauer and E. W. Dijkstra
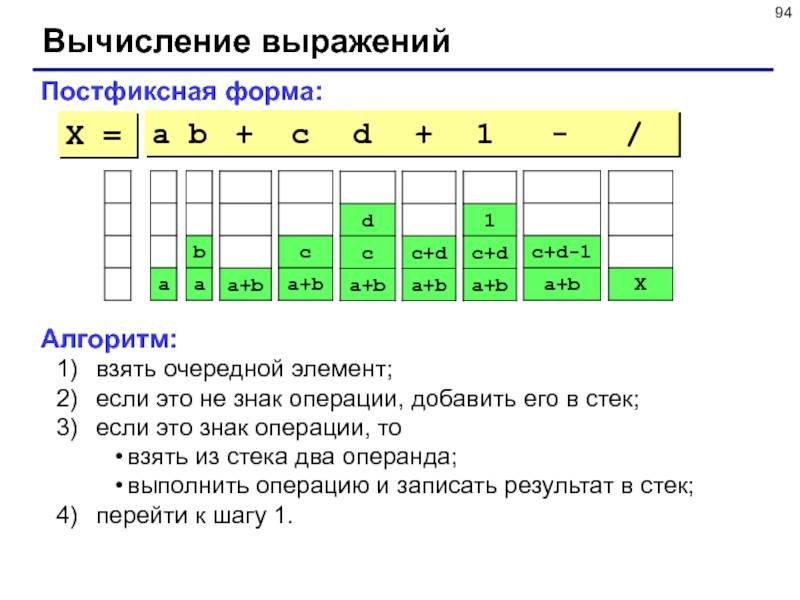
Слайд 94Вычисление выражений
Постфиксная форма:
a b + c d +
1 - /
Алгоритм:
взять очередной элемент;
если это
не знак операции, добавить его в стек;
если это знак операции, то
взять из стека два операнда;
выполнить операцию и записать результат в стек;
перейти к шагу 1.
X =
Слайд 95Вычисление выражений
Задача: в символьной строке записано правильное арифметическое выражение, которое
может содержать только однозначные числа и знаки операций +-*\. Вычислить
это выражение.
Алгоритм:
ввести строку;
построить дерево;
вычислить выражение по дереву.
Ограничения:
ошибки не обрабатываем;
многозначные числа не разрешены;
дробные числа не разрешены;
скобки не разрешены.
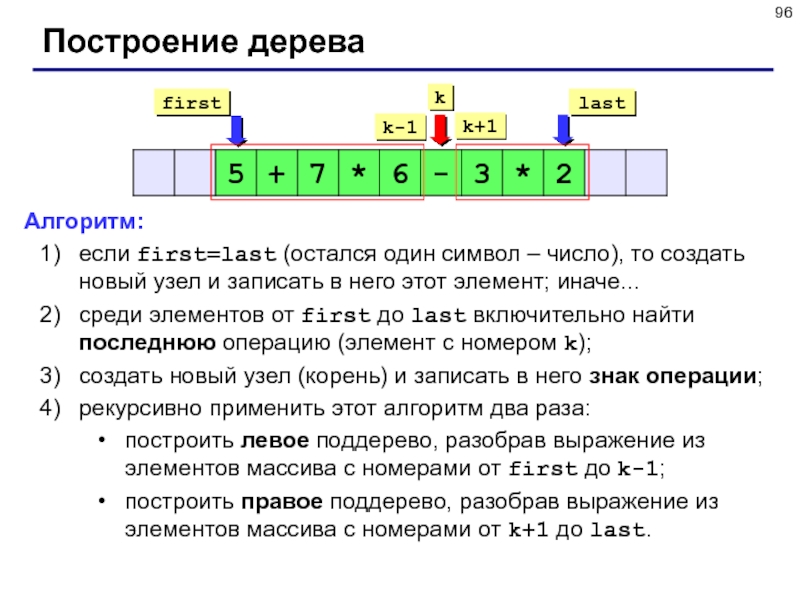
Слайд 96Построение дерева
Алгоритм:
если first=last (остался один символ – число), то создать
новый узел и записать в него этот элемент; иначе...
среди элементов
от first до last включительно найти последнюю операцию (элемент с номером k);
создать новый узел (корень) и записать в него знак операции;
рекурсивно применить этот алгоритм два раза:
построить левое поддерево, разобрав выражение из элементов массива с номерами от first до k-1;
построить правое поддерево, разобрав выражение из элементов массива с номерами от k+1 до last.
first
last
k
k+1
k-1
Слайд 97Как найти последнюю операцию?
Порядок выполнения операций
умножение и деление;
сложение и вычитание.
Приоритет
(старшинство) – число, определяющее последовательность выполнения операций: раньше выполняются операции
с большим приоритетом:
умножение и деление (приоритет 2);
сложение и вычитание (приоритет 1).
Слайд 98Приоритет операции
{ Функция Priority – приоритет операции
Вход: символ операции
Выход: приоритет или 100, если не операция }
function Priority (
c: char ): integer;
begin
case ( c ) of
'+', '-': Result := 1;
'*', '/': Result := 2;
else Result := 100;
end;
end;
сложение и вычитание: приоритет 1
умножение и деление: приоритет 2
это вообще не операция
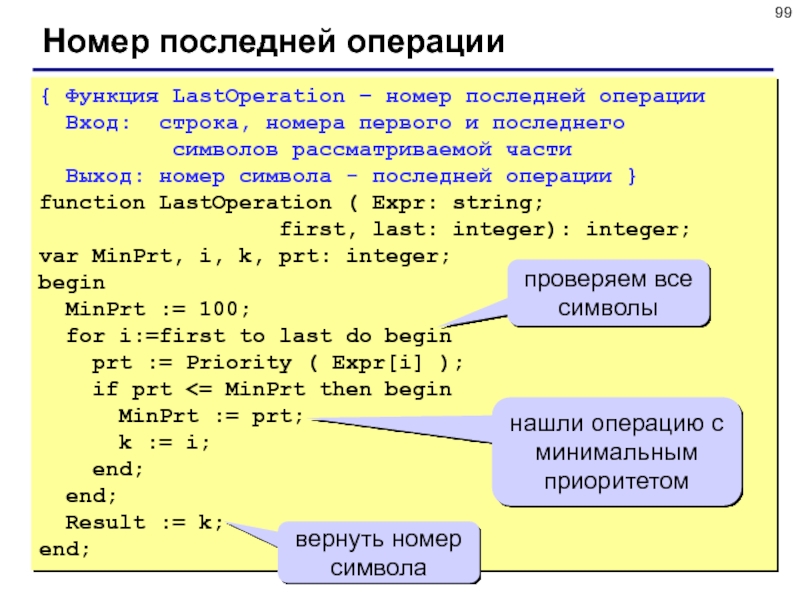
Слайд 99Номер последней операции
{ Функция LastOperation – номер последней операции
Вход:
строка, номера первого и последнего
символов
рассматриваемой части
Выход: номер символа - последней операции }
function LastOperation ( Expr: string;
first, last: integer): integer;
var MinPrt, i, k, prt: integer;
begin
MinPrt := 100;
for i:=first to last do begin
prt := Priority ( Expr[i] );
if prt <= MinPrt then begin
MinPrt := prt;
k := i;
end;
end;
Result := k;
end;
проверяем все символы
вернуть номер символа
нашли операцию с минимальным приоритетом
Слайд 100Построение дерева
Структура узла
type PNode = ^Node;
Node =
record
data: char;
left,
right: PNode;
end;
Создание узла для числа (без потомков)
function NumberNode(c: char): PNode;
begin
New(Result);
Result^.data := c;
Result^.left := nil;
Result^.right := nil;
end;
возвращает адрес созданного узла
один символ, число
Слайд 101Построение дерева
{ Функция MakeTree – построение дерева
Вход: строка, номера
первого и последнего
символов рассматриваемой части
Выход: адрес построенного дерева }
function MakeTree ( Expr: string;
first, last: integer): PNode;
var k: integer;
begin
if first = last then begin
Result := NumberNode ( Expr[first] );
Exit;
end;
k := LastOperation ( Expr, first, last );
New(Result);
Result^.data := Expr[k];
Result^.left := MakeTree ( Expr, first, k-1 );
Result^.right := MakeTree ( Expr, k+1, last );
end;
осталось только число
новый узел: операция
Слайд 102Вычисление выражения по дереву
{ Функция CalcTree – вычисление по дереву
Вход: адрес дерева
Выход: значение выражения
}
function CalcTree(Tree: PNode): integer;
var num1, num2: integer;
begin
if Tree^.left = nil then begin
Result := Ord(Tree^.data) - Ord('0');
Exit;
end;
num1 := CalcTree(Tree^.left);
num2 := CalcTree(Tree^.right);
case Tree^.data of
'+': Result := num1+num2;
'-': Result := num1-num2;
'*': Result := num1*num2;
'/': Result := num1 div num2;
else Result := MaxInt;
end;
end;
вернуть число, если это лист
вычисляем операнды (поддеревья)
выполняем операцию
некорректная операция
Слайд 103Основная программа
{ Ввод и вычисление выражения с помощью дерева }
program
qq;
var Tree: PNode;
Expr: string;
{ процедуры и функции }
begin
write('Введите выражение > ');
readln( Expr );
Tree := MakeTree( Expr, 1, Length(Expr) );
writeln(' = ', CalcTree(Tree) );
end.
Слайд 104Дерево игры
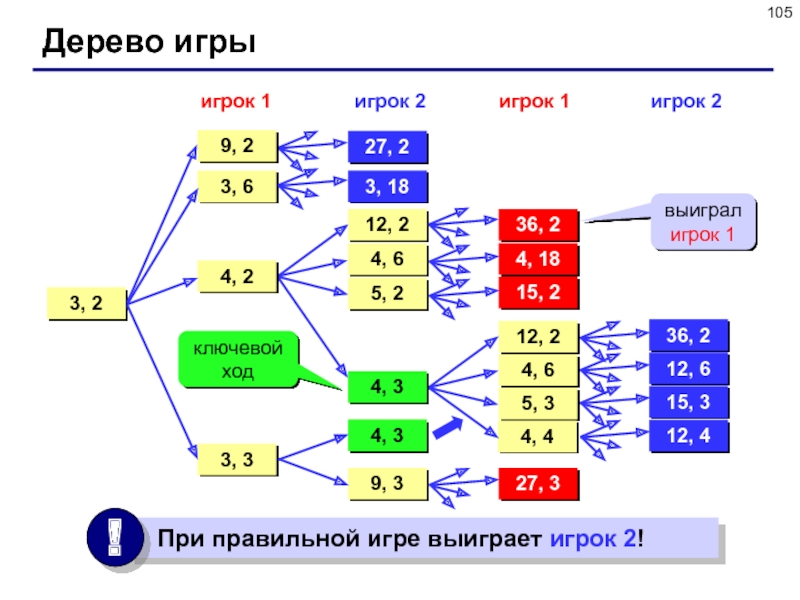
Задача.
Перед двумя игроками лежат две кучки камней, в
первой из которых 3, а во второй – 2 камня.
У каждого игрока неограниченно много камней.
Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу.
Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16.
Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Как должен ходить выигрывающий игрок?
Слайд 105Дерево игры
3, 2
игрок 1
3, 6
27, 2
3, 18
3, 3
4, 2
12, 2
4,
6
5, 2
4, 3
9, 3
4, 3
36, 2
4, 18
15, 2
27, 3
игрок 1
игрок
2
игрок 2
9, 2
4, 3
4, 3
ключевой ход
выиграл игрок 1
Слайд 106Задания
«4»: «Собрать» программу для вычисления правильного арифметического выражения, включающего только
однозначные числа и знаки операций +, -, * , /.
«5»:
То же самое, но допускаются также многозначные числа и скобки.
«6»: То же самое, что и на «5», но с обработкой ошибок (должно выводиться сообщение).
Слайд 107Тема 7. Графы
© К.Ю. Поляков, 2008-2010
Динамические структуры данных
(язык Паскаль)
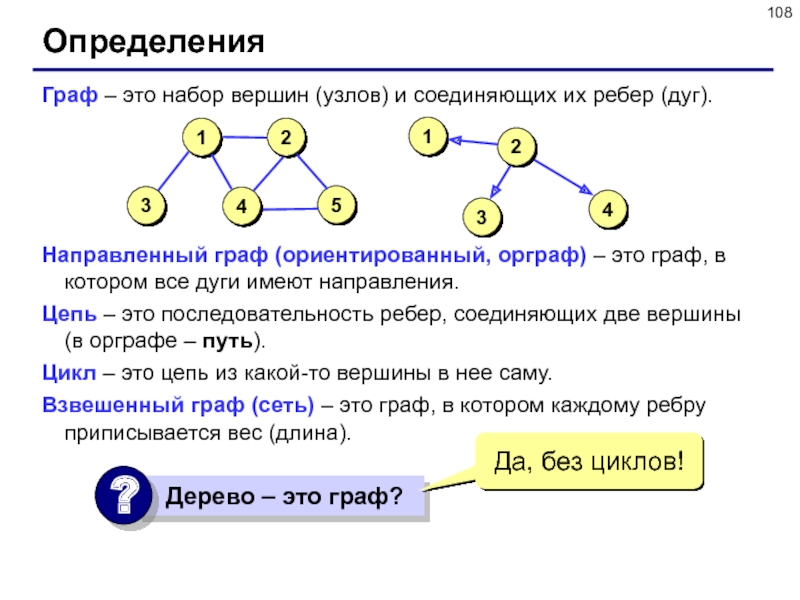
Слайд 108Определения
Граф – это набор вершин (узлов) и соединяющих их ребер
(дуг).
Направленный граф (ориентированный, орграф) – это граф, в котором
все дуги имеют направления.
Цепь – это последовательность ребер, соединяющих две вершины (в орграфе – путь).
Цикл – это цепь из какой-то вершины в нее саму.
Взвешенный граф (сеть) – это граф, в котором каждому ребру приписывается вес (длина).
Да, без циклов!
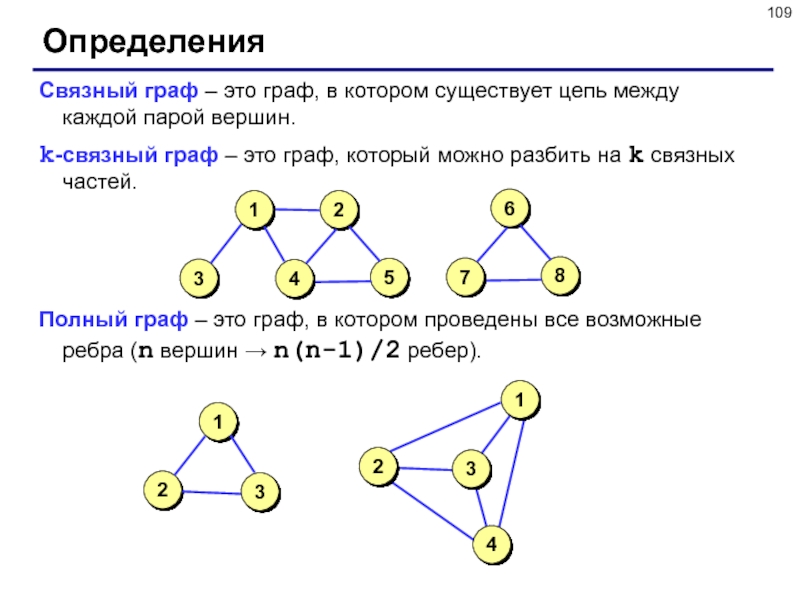
Слайд 109Определения
Связный граф – это граф, в котором существует цепь между
каждой парой вершин.
k-cвязный граф – это граф, который можно разбить
на k связных частей.
Полный граф – это граф, в котором проведены все возможные ребра (n вершин → n(n-1)/2 ребер).
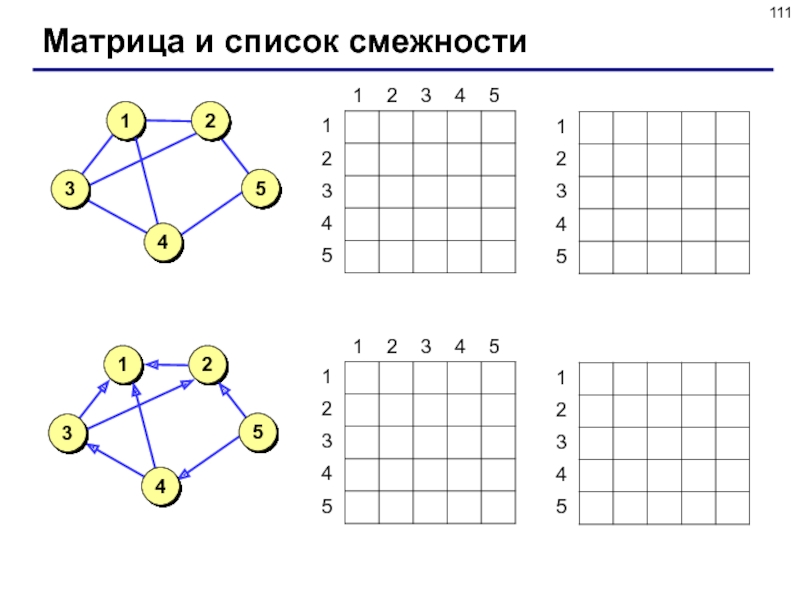
Слайд 110Описание графа
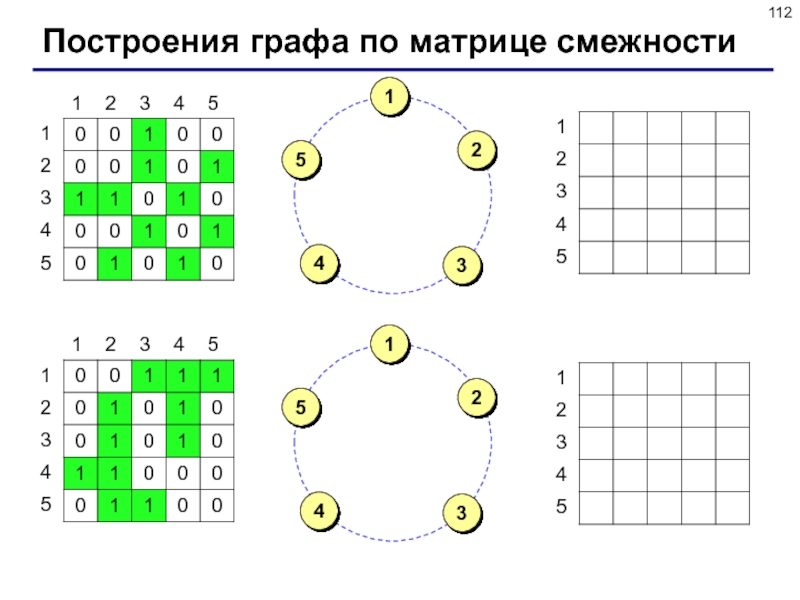
Матрица смежности – это матрица, элемент M[i][j] которой равен
1, если существует ребро из вершины i в вершину j,
и равен 0, если такого ребра нет.
Список смежности
Слайд 112Построения графа по матрице смежности
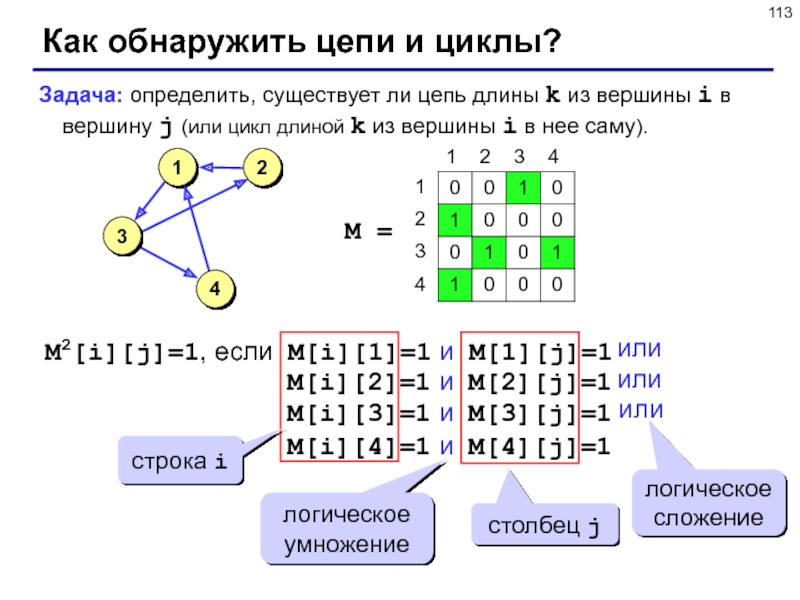
Слайд 113Как обнаружить цепи и циклы?
Задача: определить, существует ли цепь длины
k из вершины i в вершину j (или цикл длиной
k из вершины i в нее саму).
M2[i][j]=1, если M[i][1]=1 и M[1][j]=1
или
M[i][2]=1 и M[2][j]=1
или
M[i][3]=1 и M[3][j]=1
строка i
логическое умножение
столбец j
логическое сложение
M =
или
M[i][4]=1 и M[4][j]=1
Слайд 114Как обнаружить цепи и циклы?
M2 = M M
Логическое умножение
матрицы на себя:
матрица путей длины 2
M2 =
=
M2[3][1] = 0·0 +
1·1 + 0·0 + 1·1 = 1
маршрут 3-2-1
маршрут 3-4-1
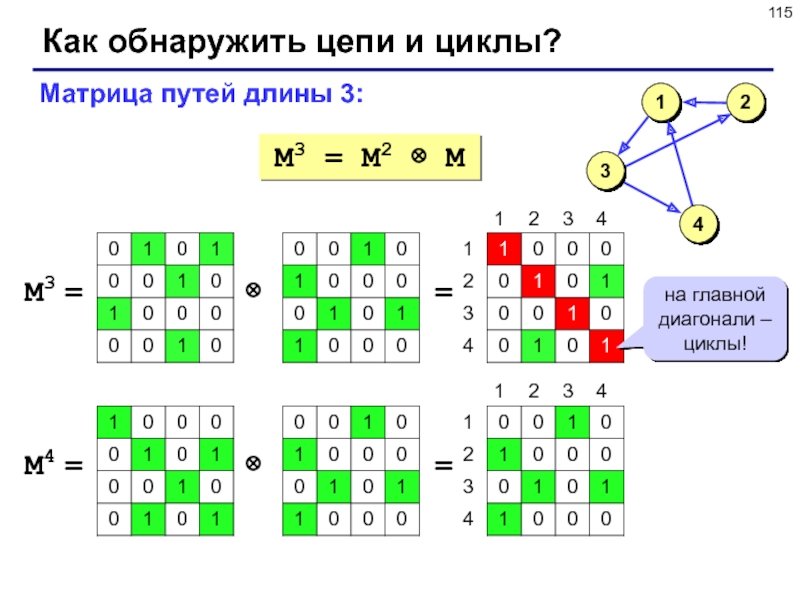
Слайд 115Как обнаружить цепи и циклы?
M3 = M2 M
Матрица путей
длины 3:
M3 =
=
на главной диагонали – циклы!
M4 =
=
Слайд 116Весовая матрица
Весовая матрица – это матрица, элемент W[i,j] которой равен
весу ребра из вершины i в вершину j (если оно
есть), или равен ∞, если такого ребра нет.
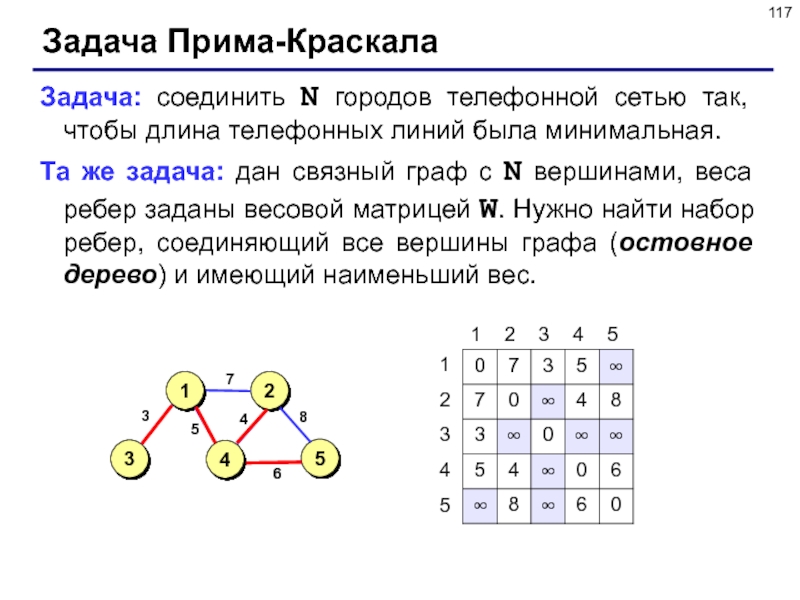
Слайд 117Задача Прима-Краскала
Задача: соединить N городов телефонной сетью так, чтобы длина
телефонных линий была минимальная.
Та же задача: дан связный граф
с N вершинами, веса ребер заданы весовой матрицей W. Нужно найти набор ребер, соединяющий все вершины графа (остовное дерево) и имеющий наименьший вес.
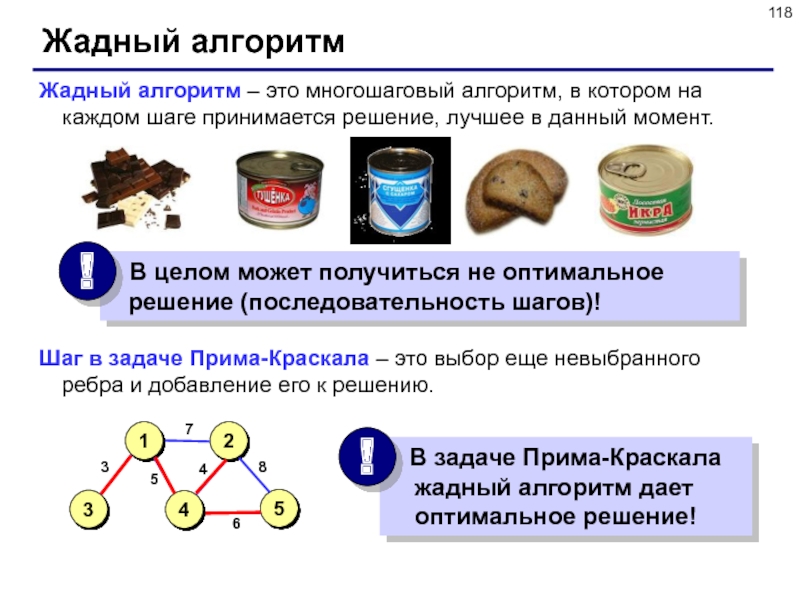
Слайд 118Жадный алгоритм
Жадный алгоритм – это многошаговый алгоритм, в котором на
каждом шаге принимается решение, лучшее в данный момент.
Шаг в
задаче Прима-Краскала – это выбор еще невыбранного ребра и добавление его к решению.
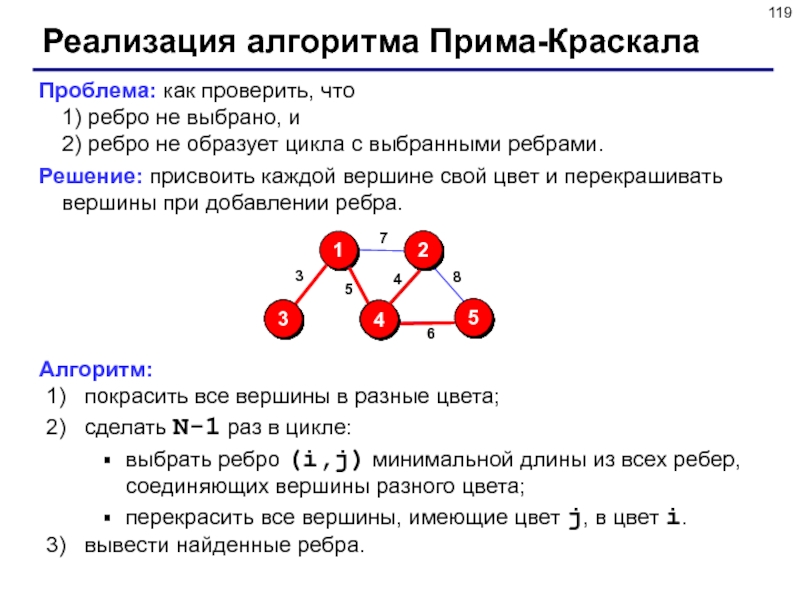
Слайд 119Реализация алгоритма Прима-Краскала
Проблема: как проверить, что
1) ребро не выбрано,
и
2) ребро не образует цикла с выбранными ребрами.
Решение:
присвоить каждой вершине свой цвет и перекрашивать вершины при добавлении ребра.
3
2
4
5
Алгоритм:
покрасить все вершины в разные цвета;
сделать N-1 раз в цикле:
выбрать ребро (i,j) минимальной длины из всех ребер, соединяющих вершины разного цвета;
перекрасить все вершины, имеющие цвет j, в цвет i.
вывести найденные ребра.
4
Слайд 120Реализация алгоритма Прима-Краскала
Структура «ребро»:
type rebro = record
i, j: integer; { номера вершин }
end;
const N = 5;
var W: array[1..N,1..N] of integer;
Color: array[1..N] of integer;
i, j, k, min, col_i, col_j: integer;
Reb: array[1..N-1] of rebro;
begin
... { здесь надо ввести матрицу W }
for i:=1 to N do { раскрасить в разные цвета }
Color[i] := i;
... { основной алгоритм – заполнение массива Reb }
... { вывести найденные ребра (массив Reb)}
end.
Основная программа:
весовая матрица
цвета вершин
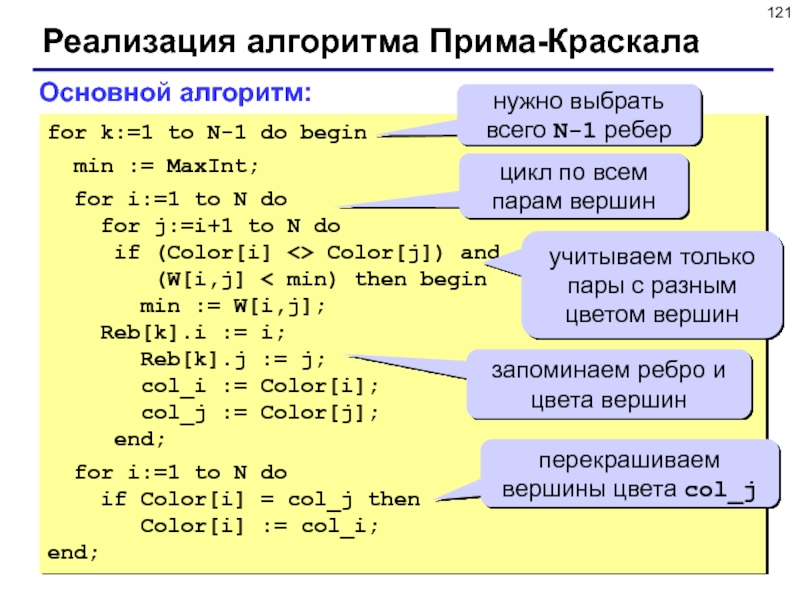
Слайд 121Реализация алгоритма Прима-Краскала
for k:=1 to N-1 do begin
min :=
MaxInt;
for i:=1 to N do
for j:=i+1 to
N do
if (Color[i] <> Color[j]) and
(W[i,j] < min) then begin
min := W[i,j];
Reb[k].i := i;
Reb[k].j := j;
col_i := Color[i];
col_j := Color[j];
end;
for i:=1 to N do
if Color[i] = col_j then
Color[i] := col_i;
end;
Основной алгоритм:
нужно выбрать
всего N-1 ребер
цикл по всем парам вершин
учитываем только пары с разным цветом вершин
запоминаем ребро и цвета вершин
перекрашиваем вершины цвета col_j
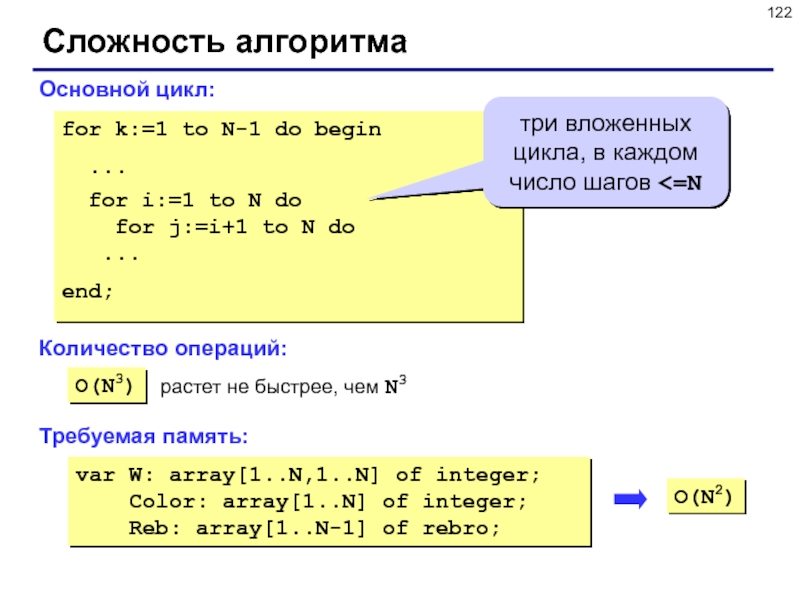
Слайд 122Сложность алгоритма
Основной цикл:
O(N3)
for k:=1 to N-1 do begin
...
for i:=1 to N do
for j:=i+1 to N
do
...
end;
три вложенных цикла, в каждом число шагов <=N
растет не быстрее, чем N3
Требуемая память:
var W: array[1..N,1..N] of integer;
Color: array[1..N] of integer;
Reb: array[1..N-1] of rebro;
O(N2)
Количество операций:
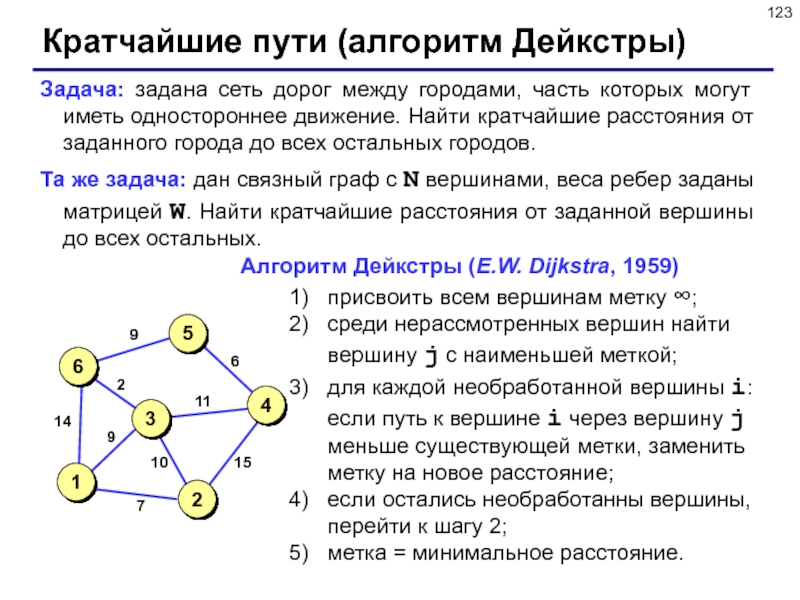
Слайд 123Кратчайшие пути (алгоритм Дейкстры)
Задача: задана сеть дорог между городами, часть
которых могут иметь одностороннее движение. Найти кратчайшие расстояния от заданного
города до всех остальных городов.
Та же задача: дан связный граф с N вершинами, веса ребер заданы матрицей W. Найти кратчайшие расстояния от заданной вершины до всех остальных.
присвоить всем вершинам метку ∞;
среди нерассмотренных вершин найти вершину j с наименьшей меткой;
для каждой необработанной вершины i: если путь к вершине i через вершину j меньше существующей метки, заменить метку на новое расстояние;
если остались необработанны вершины, перейти к шагу 2;
метка = минимальное расстояние.
Алгоритм Дейкстры (E.W. Dijkstra, 1959)
Слайд 125Реализация алгоритма Дейкстры
Массивы:
массив a, такой что a[i]=1, если вершина уже
рассмотрена, и a[i]=0, если нет.
массив b, такой что b[i] –
длина текущего кратчайшего пути из заданной вершины x в вершину i;
массив c, такой что c[i] – номер вершины, из которой нужно идти в вершину i в текущем кратчайшем пути.
Инициализация:
заполнить массив a нулями (вершины не обработаны);
записать в b[i] значение W[x][i];
заполнить массив c значением x;
записать a[x]=1.
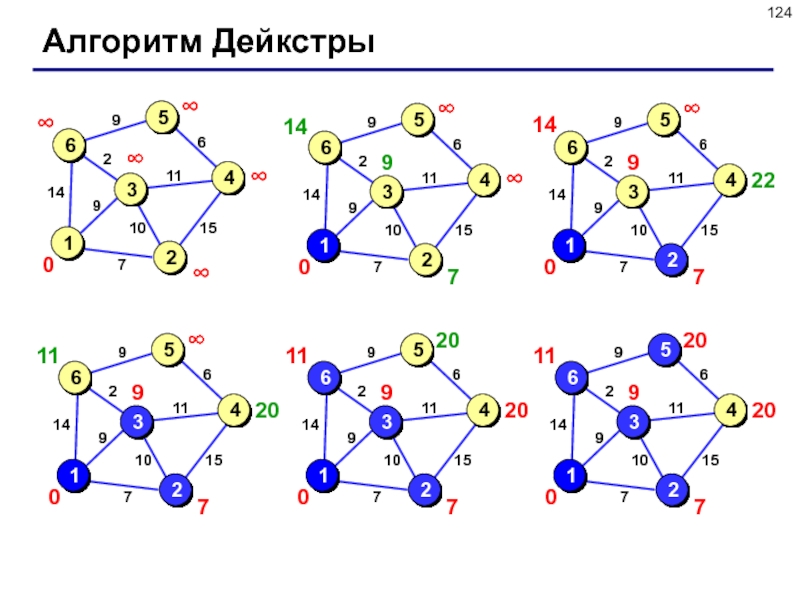
Слайд 126Реализация алгоритма Дейкстры
Основной цикл:
если все вершины рассмотрены, то стоп.
среди всех
нерассмотренных вершин (a[i]=0) найти вершину j, для которой b[i] –
минимальное;
записать a[j]:=1;
для всех вершин k: если путь в вершину k через вершину j короче, чем найденный ранее кратчайший путь, запомнить его: записать b[k]:=b[j]+W[j,k] и c[k]=j.
Шаг 1:
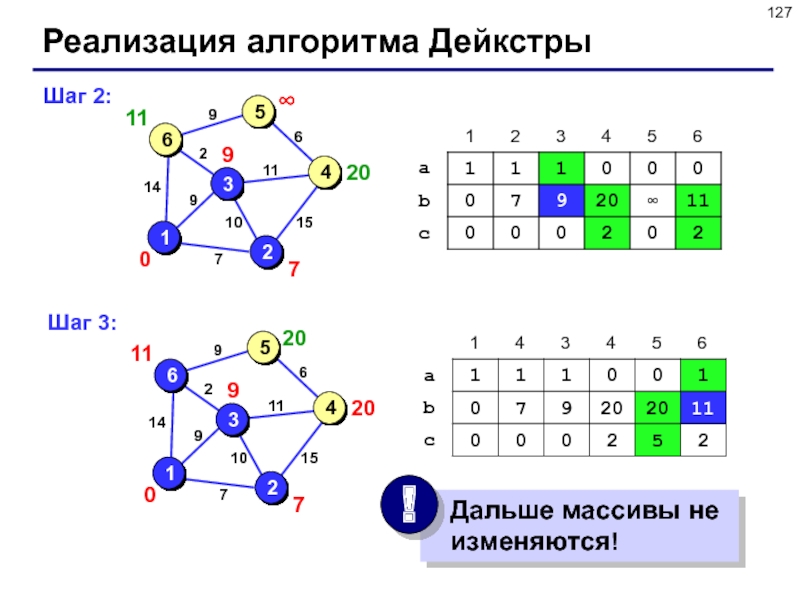
Слайд 127Реализация алгоритма Дейкстры
Шаг 2:
Шаг 3:
Слайд 128Как вывести маршрут?
Результат работа алгоритма Дейкстры:
длины путей
Маршрут из вершины 0
в вершину 4:
4
5
2
0
Сложность алгоритма Дейкстры:
O(N2)
два вложенных цикла по N шагов
Вывод
маршрута в вершину i (использование массива c):
установить z:=i;
пока c[i]<>x присвоить z:=c[z] и вывести z.
Слайд 129Алгоритм Флойда-Уоршелла
Задача: задана сеть дорог между городами, часть которых могут
иметь одностороннее движение. Найти все кратчайшие расстояния, от каждого города
до всех остальных городов.
for k: =1 to N
for i: = 1 to N
for j: = 1 to N
if W[i,j] > W[i,k] + W[k,j] then
W[i,j] := W[i,k] + W[k,j];
Если из вершины i в вершину j короче ехать через вершину k, мы едем через вершину k!
Слайд 130Алгоритм Флойда-Уоршелла
Версия с запоминанием маршрута:
for i:= 1 to N
for
j := 1 to N
c[i,j] := i;
...
for
k: =1 to N
for i: = 1 to N
for j: = 1 to N
if W[i,j] > W[i,k] + W[k,j] then begin
W[i,j] := W[i,k] + W[k,j];
c[i,j] := c[k,j];
end;
i–ая строка строится так же, как массив c в алгоритме Дейкстры
в конце цикла c[i,j] – предпоследняя вершина в кратчайшем маршруте из вершины i в вершину j
c[i,j] := c[k,j];
O(N3)
Слайд 131Задача коммивояжера
Задача коммивояжера. Коммивояжер (бродячий торговец) должен выйти из первого
города и, посетив по разу в неизвестном порядке города 2,3,...N,
вернуться обратно в первый город. В каком порядке надо обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
Точные методы:
простой перебор;
метод ветвей и границ;
метод Литтла;
…
Приближенные методы:
метод случайных перестановок (Matlab);
генетические алгоритмы;
метод муравьиных колоний;
…
большое время счета для больших N
O(N!)
не гарантируется оптимальное решение
Слайд 132Другие классические задачи
Задача на минимум суммы. Имеется N населенных пунктов,
в каждом из которых живет pi школьников (i=1,...,N). Надо разместить
школу в одном из них так, чтобы общее расстояние, проходимое всеми учениками по дороге в школу, было минимальным.
Задача о наибольшем потоке. Есть система труб, которые имеют соединения в N узлах. Один узел S является источником, еще один – стоком T. Известны пропускные способности каждой трубы. Надо найти наибольший поток от источника к стоку.
Задача о наибольшем паросочетании. Есть M мужчин и N женщин. Каждый мужчина указывает несколько (от 0 до N) женщин, на которых он согласен жениться. Каждая женщина указывает несколько мужчин (от 0 до M), за которых она согласна выйти замуж. Требуется заключить наибольшее количество моногамных браков.






![Динамические структуры данных (язык Паскаль) Обращение к данным (массивы)program qq;var i: integer; A: array[1..4] of integer; Обращение к данным (массивы)program qq;var i: integer; A: array[1..4] of integer; pI: ^integer;begin for i:=1](/img/thumbs/b483da058fd1dcc239196b6f5b421f91-800x.jpg)



![Динамические структуры данных (язык Паскаль) Использование указателей (Delphi)program qq;type intArray = array[1..1] of integer;var A: ^intArray; Использование указателей (Delphi)program qq;type intArray = array[1..1] of integer;var A: ^intArray; i, N: integer;begin writeln('Размер массива>');](/img/thumbs/658f86e8145402b0f38fd5e4f8d33540-800x.jpg)








![Динамические структуры данных (язык Паскаль) Массив записейОбъявление (выделение памяти):const N = 10;var aBooks: array[1..N] of record Массив записейОбъявление (выделение памяти):const N = 10;var aBooks: array[1..N] of record author: string[40];](/img/thumbs/3062f7fab75a478d77825bab655ba4f5-800x.jpg)
![Динамические структуры данных (язык Паскаль) Массив записейfor i:=1 to N do begin readln(aBooks[i].author); readln(aBooks[i].title); ...end;for i:=1 Массив записейfor i:=1 to N do begin readln(aBooks[i].author); readln(aBooks[i].title); ...end;for i:=1 to N do if](/img/thumbs/e058620c42e4fce1a3f3cab3fb0d077f-800x.jpg)
![Динамические структуры данных (язык Паскаль) Новый тип данных – записьconst N = 10;var Book: TBook; // Новый тип данных – записьconst N = 10;var Book: TBook; // одна запись aBooks: array[1..N] of](/img/thumbs/ae58a80670ea12e7e757ba82fbd23526-800x.jpg)





![Динамические структуры данных (язык Паскаль) Сортировка массива записейfor i:=1 to N-1 do for j:=N-1 downto i Сортировка массива записейfor i:=1 to N-1 do for j:=N-1 downto i do if aBooks[j].year](/img/thumbs/0852a635d81be2cbeb0fbb2c2ea00d63-800x.jpg)

![Динамические структуры данных (язык Паскаль) Реализация в программеtype PBook = ^TBook; { новый тип данных }var Реализация в программеtype PBook = ^TBook; { новый тип данных }var p: array[1..N] of PBook; begin](/img/thumbs/40d04d7a61a5de2bc2a4c7407dbaa07c-800x.jpg)















![Динамические структуры данных (язык Паскаль) Пример задачиЗадача: вводится символьная строка, в которой записано выражение со скобками Пример задачиЗадача: вводится символьная строка, в которой записано выражение со скобками трех типов: [], {} и ().](/img/thumbs/33da07ba4c7ed840443dd28ef8ed27f7-800x.jpg)










![Динамические структуры данных (язык Паскаль) Реализация очереди (кольцевой массив)type Queue = record data: array[1..MAXSIZE] of Реализация очереди (кольцевой массив)type Queue = record data: array[1..MAXSIZE] of integer;](/img/thumbs/578ab766882d3726a6e91ebdef9e7078-800x.jpg)


















![Динамические структуры данных (язык Паскаль) Описание графаМатрица смежности – это матрица, элемент M[i][j] которой равен 1, Описание графаМатрица смежности – это матрица, элемент M[i][j] которой равен 1, если существует ребро из вершины i](/img/thumbs/b629fd3d46871eaeeca44822a2da6db2-800x.jpg)
![Динамические структуры данных (язык Паскаль) Как обнаружить цепи и циклы?M2 = M MЛогическое умножение матрицы Как обнаружить цепи и циклы?M2 = M MЛогическое умножение матрицы на себя:матрица путей длины 2M2 ==M2[3][1]](/img/thumbs/fe72ea7792d13c74796dc46c4258422d-800x.jpg)
![Динамические структуры данных (язык Паскаль) Весовая матрицаВесовая матрица – это матрица, элемент W[i,j] которой равен весу Весовая матрицаВесовая матрица – это матрица, элемент W[i,j] которой равен весу ребра из вершины i в вершину](/img/thumbs/75f83d164d7fed28eea09d8e97bd6143-800x.jpg)

![Динамические структуры данных (язык Паскаль) Реализация алгоритма ДейкстрыМассивы:массив a, такой что a[i]=1, если вершина уже рассмотрена, Реализация алгоритма ДейкстрыМассивы:массив a, такой что a[i]=1, если вершина уже рассмотрена, и a[i]=0, если нет.массив b, такой](/img/thumbs/47d7013a602debce84230f402398d931-800x.jpg)
![Динамические структуры данных (язык Паскаль) Реализация алгоритма ДейкстрыОсновной цикл:если все вершины рассмотрены, то стоп.среди всех нерассмотренных Реализация алгоритма ДейкстрыОсновной цикл:если все вершины рассмотрены, то стоп.среди всех нерассмотренных вершин (a[i]=0) найти вершину j, для](/img/thumbs/c4cbb029523b670676fa8228524c7b89-800x.jpg)


![Динамические структуры данных (язык Паскаль) Алгоритм Флойда-УоршеллаВерсия с запоминанием маршрута:for i:= 1 to N for j Алгоритм Флойда-УоршеллаВерсия с запоминанием маршрута:for i:= 1 to N for j := 1 to N c[i,j]](/img/thumbs/8d612d529406de6017ecebed13eb8186-800x.jpg)