Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамическое программирование АНАЛОГИИ
Содержание
- 1. Динамическое программирование АНАЛОГИИ
- 2. 03.03.2014Динамическое программированиеАНАЛОГИИРешение методом динамического программированияЗадачи:Перемножение цепочки матрицОптимальные
- 3. 03.03.2014Динамическое программированиеОценка количества узлов дереваОценить количество узлов
- 4. 03.03.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2,
- 5. 03.03.2014Динамическое программированиеНесколько первых чисел КаталанаСр. Сn –1 и
- 6. 03.03.2014Динамическое программированиеЧисло bn структурно различных бинарных деревьев
- 7. 03.03.2014Динамическое программированиеb2 = b0 b1 + b1 b0 = 2, b3 = b0 b2 + b1 b1 + b2 b0 = 5,b4 = b0 b3 + b1 b2 + b2 b1 + b3 b0 = = 5 + 2
- 8. Решение методом динамического программированияСтруктура оптимального решенияРекуррентное соотношениеВычисление
- 9. 03.03.2014Динамическое программированиеЗадача: оптимальная триангуляция выпуклого многоугольникавершиныстороныПростой многоугольник (без самопересечений)Выпуклый многоугольникНевыпуклый многоугольникдиагонали
- 10. 03.03.2014Динамическое программированиеТриангуляция (диагонали не пересекаются внутри многоугольника)Задача:
- 11. 03.03.2014Динамическое программированиеНа треугольниках определена весовая функция w(Δvivjvk)
- 12. 03.03.2014Динамическое программированиеКоличество способов триангуляцииВершин n, диаг. =
- 13. 03.03.2014Динамическое программированиеКоличество способов триангуляцииn = 6, диаг.
- 14. 03.03.2014Динамическое программированиеРекуррентная формула для веса оптимальной триангуляции
- 15. 03.03.2014Динамическое программированиеУпражненияДоказать что триангуляция n – угольника
- 16. 03.03.2014Динамическое программированиеСвязь задач123450M1M2M3M4M5 (M1 M2) (( M3
- 17. 03.03.2014Динамическое программированиеСвязь задач123450(M1 M2) (( M3 M4)
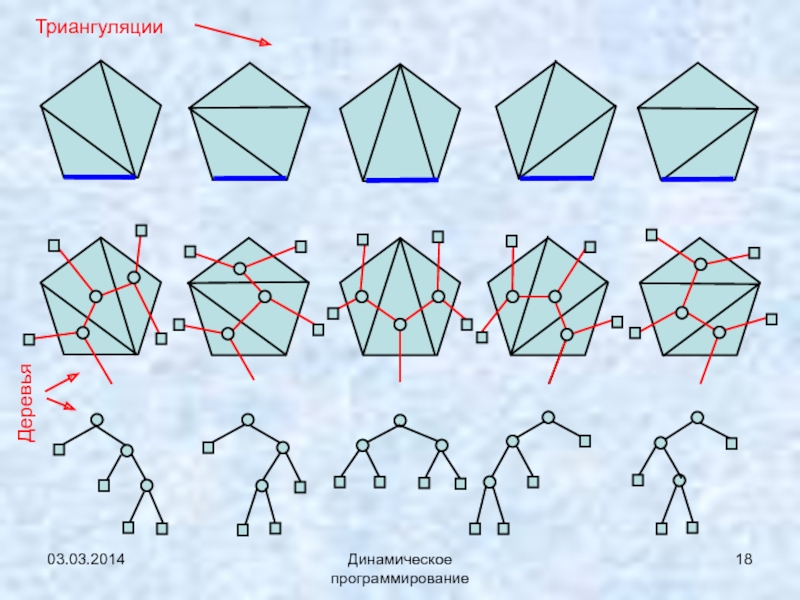
- 18. 03.03.2014Динамическое программированиеТриангуляцииДеревья
- 19. 03.03.2014Динамическое программирование0 1 0 1 0 10
- 20. 03.03.2014Динамическое программированиеКОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 103.03.2014
Динамическое программирование
Построение и анализ алгоритмов
Лекция 4.3
Динамическое программирование
АНАЛОГИИ
Слайд 203.03.2014
Динамическое программирование
АНАЛОГИИ
Решение методом динамического программирования
Задачи:
Перемножение цепочки матриц
Оптимальные БДП
Задача Х и
т.п.
расстановка»Слайд 303.03.2014
Динамическое программирование
Оценка количества узлов дерева
Оценить количество узлов дерева в общем
случае можно подсчетом всех возможных вариантов расстановок скобок в произведении
матриц.Пусть pn – число вариантов расстановок скобок в произведении n сомножителей (включая самые внешние скобки).
Например, для трех сомножителей abc имеем два варианта (a(bc)) и ((ab)c), а следовательно, p3 = 2.
В общем случае, считая, что «последнее» по порядку умножение может оказаться на любом из n –1 мест, запишем следующее рекуррентное соотношение:
pn = p1 pn –1 + p2 pn –2 + … + pn –2 p2 + p n –1 p1.
Из лекции про перемножение матриц
Слайд 403.03.2014
Динамическое программирование
Начальное условие p1 = 1. Далее
p2 = p1 p1 = 1,
p3 = p1 p2 + p2 p1 = 2,
p4 = p1 p3 + p2 p2 + p3 p1 = 5.
Оказывается [7,
с. 393], что решением этого рекуррентного уравнения являются так называемые числа
Каталана pn = Сn –1, где Сn =(2 k | k) / (k +1),а запись (n | m) обозначает биномиальный коэффициент (n | m) = n!/(m! (n – m)!).
При больших значениях n справедливо
т. е. число узлов в дереве перебора есть экспоненциальная функция от n.
Из лекции про перемножение матриц
Слайд 503.03.2014
Динамическое программирование
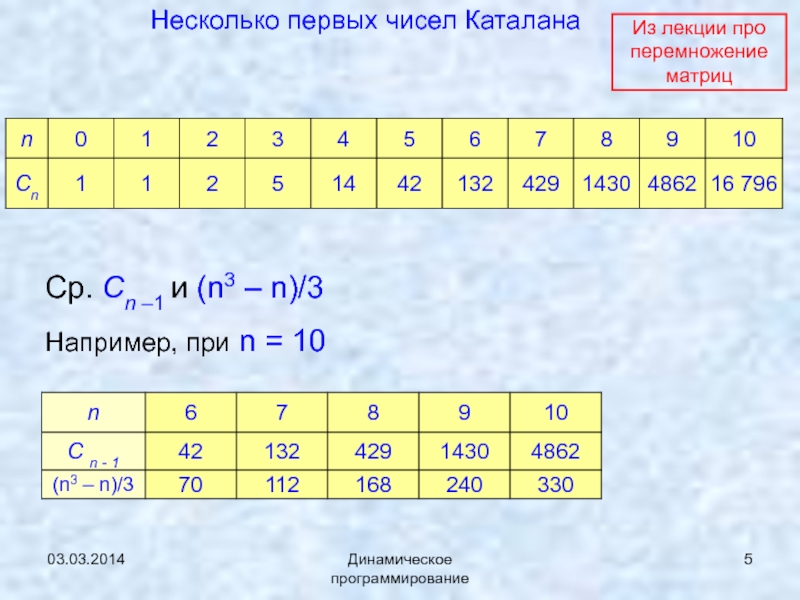
Несколько первых чисел Каталана
Ср. Сn –1 и (n3 – n)/3
Например, при n = 10
Из лекции про перемножение матриц
Слайд 603.03.2014
Динамическое программирование
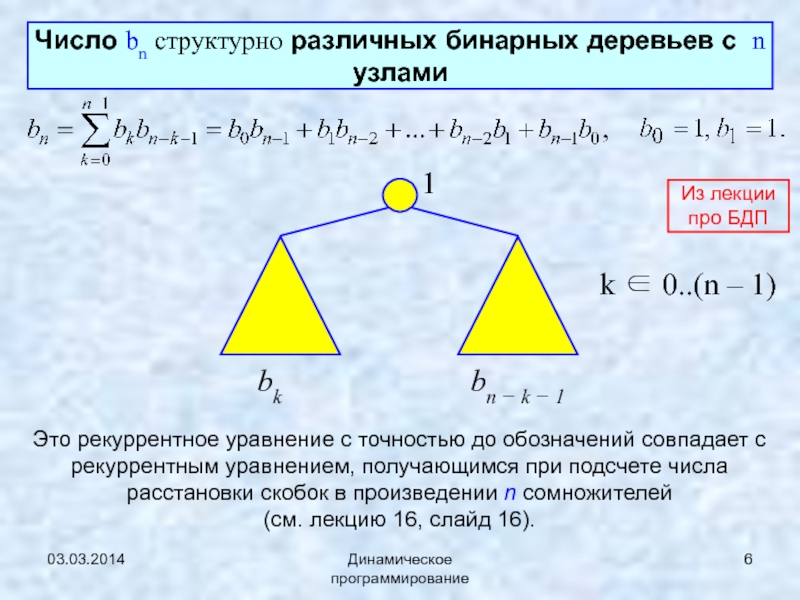
Число bn структурно различных бинарных деревьев с n узлами
bk
bn − k − 1
1
k ∈ 0..(n – 1)
Это рекуррентное уравнение с точностью до обозначений совпадает с рекуррентным уравнением, получающимся при подсчете числа расстановки скобок в произведении n сомножителей
(см. лекцию 16, слайд 16).
Из лекции про БДП
Слайд 703.03.2014
Динамическое программирование
b2 = b0 b1 + b1 b0 = 2,
b3 = b0 b2 + b1 b1 + b2 b0 = 5,
b4 = b0 b3 + b1 b2 + b2 b1 + b3 b0 =
= 5 + 2 + 2 +
5 = 14
Решением рекуррентного уравнения являются так называемые числа Каталана
Сn, т. е. bn = Сn. Ранее (Лекция 13, слайды хх, хх) были приведены: общая формула для чисел Каталана и асимптотическое соотношение
Из лекции про БДП
Слайд 8Решение методом динамического программирования
Структура оптимального решения
Рекуррентное соотношение
Вычисление оптимальной стоимости (по
рекуррентному соотношению)
Построение оптимального решения
Проиллюстрировать на предыдущих примерах
03.03.2014
Динамическое программирование
Слайд 903.03.2014
Динамическое программирование
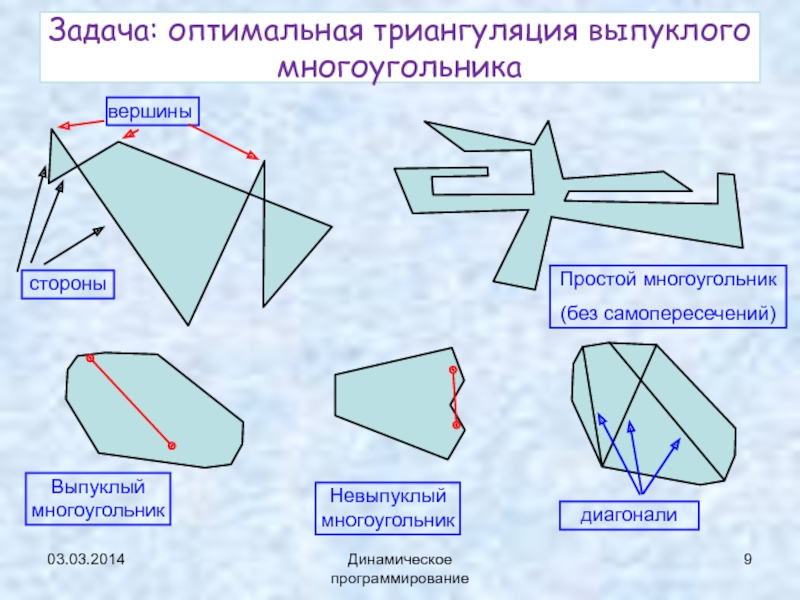
Задача: оптимальная триангуляция выпуклого многоугольника
вершины
стороны
Простой многоугольник
(без самопересечений)
Выпуклый
многоугольник
Невыпуклый многоугольник
диагонали
Слайд 1003.03.2014
Динамическое программирование
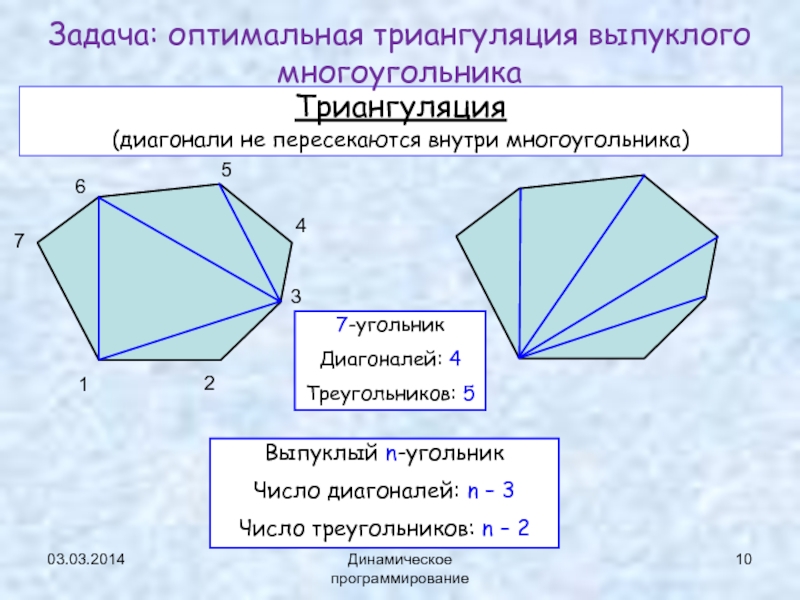
Триангуляция
(диагонали не пересекаются внутри многоугольника)
Задача: оптимальная триангуляция выпуклого
многоугольника
Выпуклый n-угольник
Число диагоналей: n – 3
Число треугольников: n –
27-угольник
Диагоналей: 4
Треугольников: 5
1
2
3
4
5
6
7
Слайд 1103.03.2014
Динамическое программирование
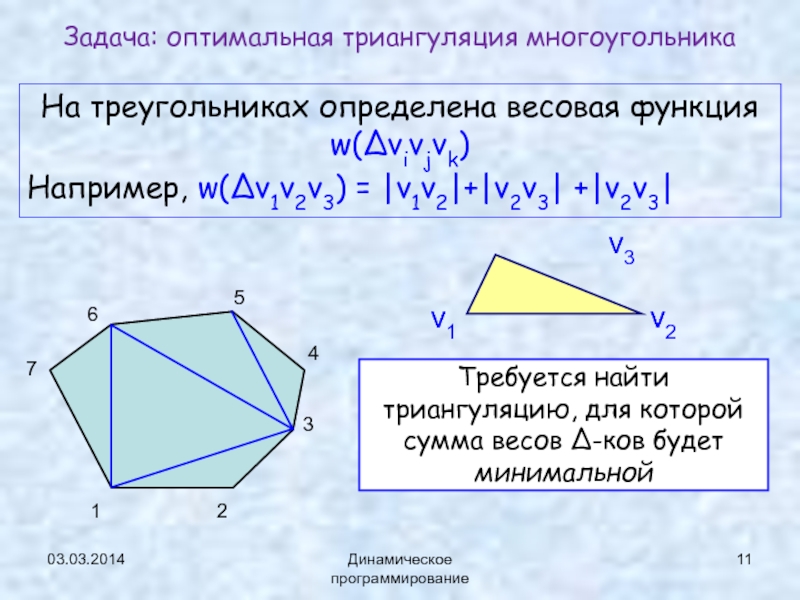
На треугольниках определена весовая функция w(Δvivjvk)
Например, w(Δv1v2v3) =
⎪v1v2⎪+⎪v2v3⎪ +⎪v2v3⎪
Задача: оптимальная триангуляция многоугольника
Требуется найти триангуляцию, для которой сумма
весов Δ-ков будет минимальнойv1
v2
v3
Слайд 1203.03.2014
Динамическое программирование
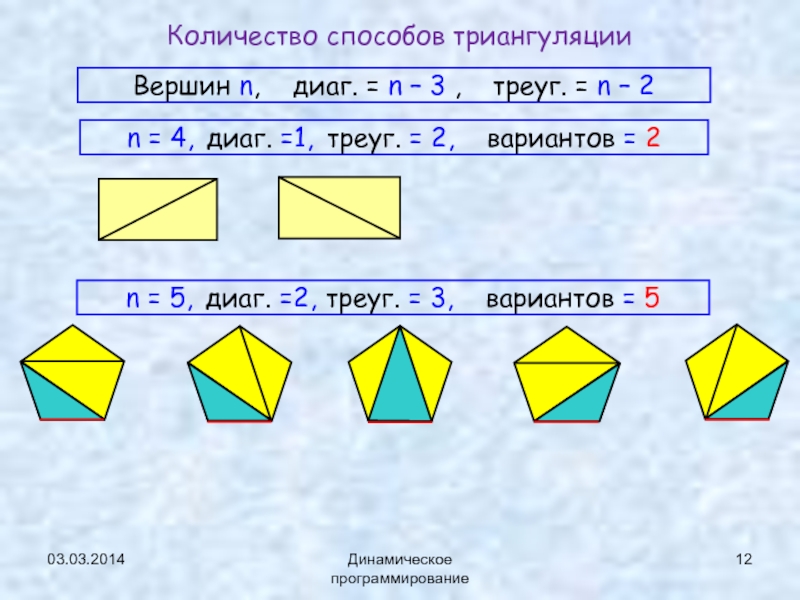
Количество способов триангуляции
Вершин n, диаг. = n – 3
, треуг. = n – 2
n = 4, диаг.
=1, треуг. = 2, вариантов = 2n = 5, диаг. =2, треуг. = 3, вариантов = 5
Слайд 1303.03.2014
Динамическое программирование
Количество способов триангуляции
n = 6, диаг. =3, треуг. =
4, вариантов = 14
5
5
2
2
1
1
d6 = d2d5 + d3d4 + d4d3 +
d5d2Слайд 1403.03.2014
Динамическое программирование
Рекуррентная формула для веса оптимальной триангуляции многоугольника (ОТМ)
mij –
вес ОТМ (vi-1,vi,…,vj)
m1n – вес ОТМ (v0,v1,…,vn)
Для двуугольника w(vi-1,vi)=0
Время
≈С1n3, память ≈С2n2vi-1
vj
vk
Слайд 1503.03.2014
Динамическое программирование
Упражнения
Доказать что триангуляция n – угольника содержит n-2 треугольника
и n-3 диагоналей.
Пусть вес треугольника = его площади. Можно ли
упростить алгоритм поиска ОТМ?Весовая функция определена на множестве диагоналей многоугольника. ОТМ – сумма весов диагоналей минимальна. Как свести эту задачу к рассмотренной?
Слайд 1603.03.2014
Динамическое программирование
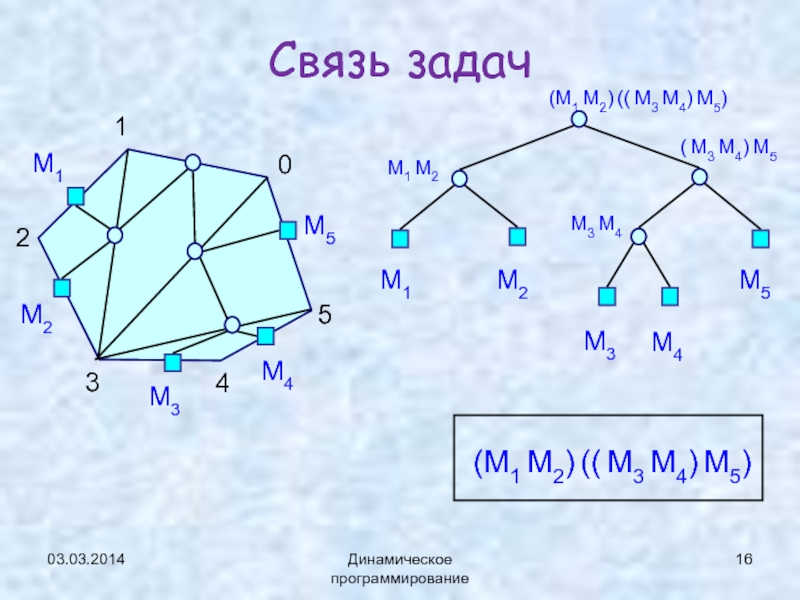
Связь задач
1
2
3
4
5
0
M1
M2
M3
M4
M5
(M1 M2) (( M3 M4) M5)
M1
M2
M3
M4
M5
M1 M2
M3
M4
( M3 M4) M5
(M1 M2) (( M3 M4) M5)
Слайд 1703.03.2014
Динамическое программирование
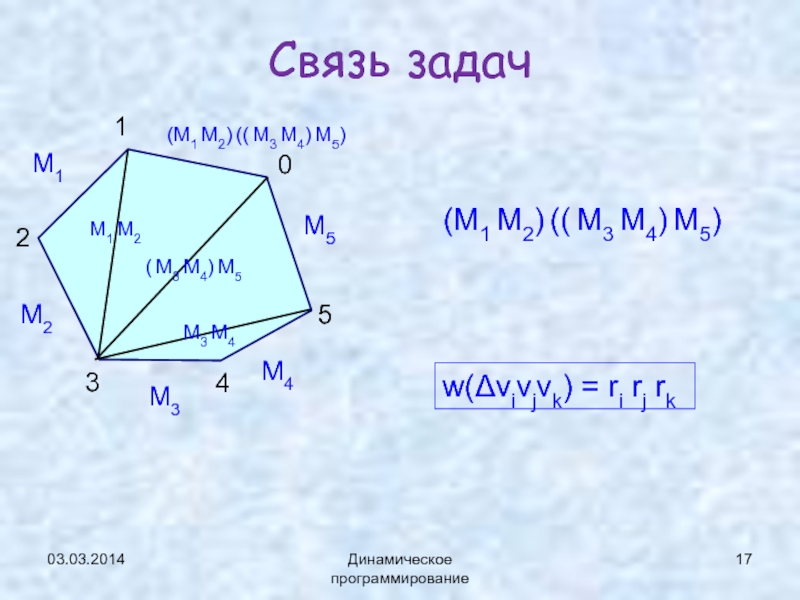
Связь задач
1
2
3
4
5
0
(M1 M2) (( M3 M4) M5)
M1
M2
M3
M4
M5
M1 M2
M3 M4
(
M3 M4) M5
(M1 M2) (( M3 M4) M5)
w(Δvivjvk) = ri
rj rkСлайд 1903.03.2014
Динамическое программирование
0 1 0 1 0 1
0 1 0 0
1 1
0 0 1 1 0 1
0 0 0 1
1 10
1
0 0 1 0 1 1
Коды
Пути в решетке
Слоистая сеть (спец. вида)



![Динамическое программирование АНАЛОГИИ 03.03.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2, p4 = p1 p3 + p2 p2 + p3 p1 = 5. Оказывается [7, с. 393], 03.03.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2, p4 = p1 p3 + p2 p2 + p3 p1 = 5. Оказывается [7, с. 393], что решением этого рекуррентного уравнения являются](/img/thumbs/72881051b7e98579045eaaa22747cde4-800x.jpg)