Слайд 1Динамика пограничного слоя атмосферы
Слайд 2Основные вопросы:
Определение понятия планетарный и внутренний ПС, значение для атмосферы,
специфические процессы
Тепловой и динамический ПС. Суточный ход стратификации в ПС
Что
такое динамическая турбулентность?Смысл и определение числа Рейнольдса
Что такое конвективная турбулентность?Смысл и определение числа Реллея (Грасгофа)
Назначение, смысл и определение числа Ричардсона
Методика получения уравненией турбулентного ПС
Суть проблемы замыкания
Уравнение баланса энергии турбулентности (смысл слагаемых)
Уметь оценить значение интегрального к-та турбулентности (ф-ла Лайхтмана)
Постановка и решение задачи Экмана.
Свойства «спирали Экмана»
Вертикальные токи на верхней границе экмановского ПС и понятие «экмановское накачивание»
Слайд 3
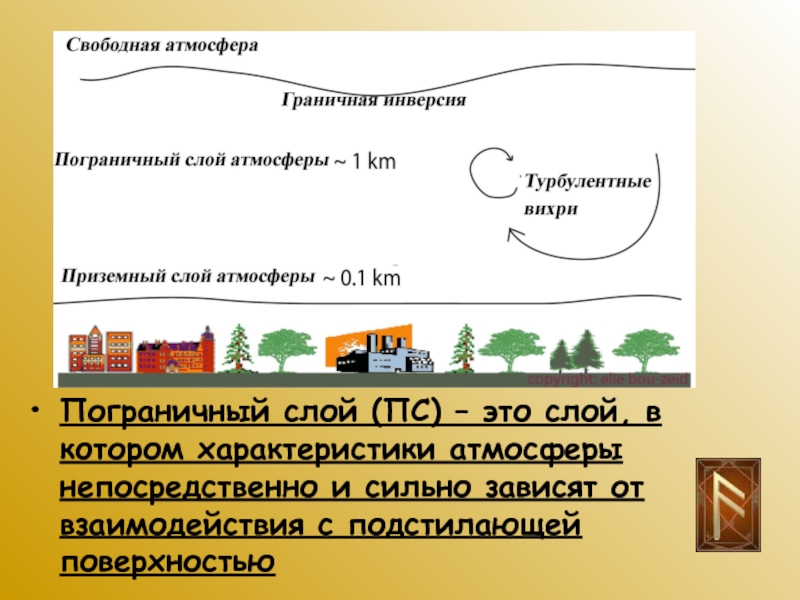
Пограничный слой (ПС) – это слой, в котором характеристики атмосферы
непосредственно и сильно зависят от взаимодействия с подстилающей поверхностью
Слайд 4Значение ПС
Через него происходит приспособление атмосферы к свойствам подстилающей поверхности
В
нем наблюдается суточный ход метеорологических характеристик
В нем генерируется турбулентность
Он определяет
интенсивность потоков тепла, влаги и аэрозолей в атмосферу
Слайд 5Планетарный пограничный слой
Охватывает всю Землю
Имеет перменную толщину
Содержит внутренние пограничные слои
Подстилается
приземным слоем
Слайд 6Горизонтальная неоднородность пп – причина образования внутренних пограничных слоев
Слайд 7Атмосферные явления связанные с внутренними пограничными слоями
Прибрежные фронты
Приморские бризовые циркуляции
Озерные
бризы
Фронты порывистости
Конвективные явления - горизонтальные вихри «роллы», открытые/закрытые конвективные ячейки
Антропогенные
острова тепла
Местные циркуляции над неоднородной подстилающей поверхностью
Горно-долинные и стоковые ветры
Слайд 8Масштабы внутри ПС, вязкий подслой
Пограничный слой (ПС) – это слой,
в котором характеристики атмосферы непосредственно и сильно зависят от взаимодействия
с подстилающей поверхностью
В конечном счете, это взаимодействие определяется молекулярной вязкостью, но она сосредоточена только в тонком вязком подслое
Выше него атмосферу уже можно считать идеальной жидкостью
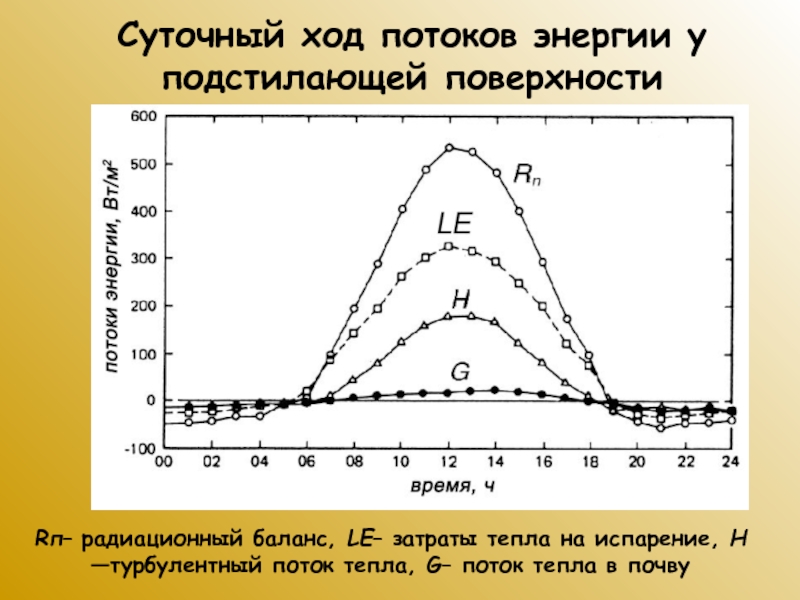
Слайд 9Суточный ход потоков энергии у подстилающей поверхности
Rп– радиационный баланс, LE–
затраты тепла на испарение, H —турбулентный поток тепла, G– поток
тепла в почву
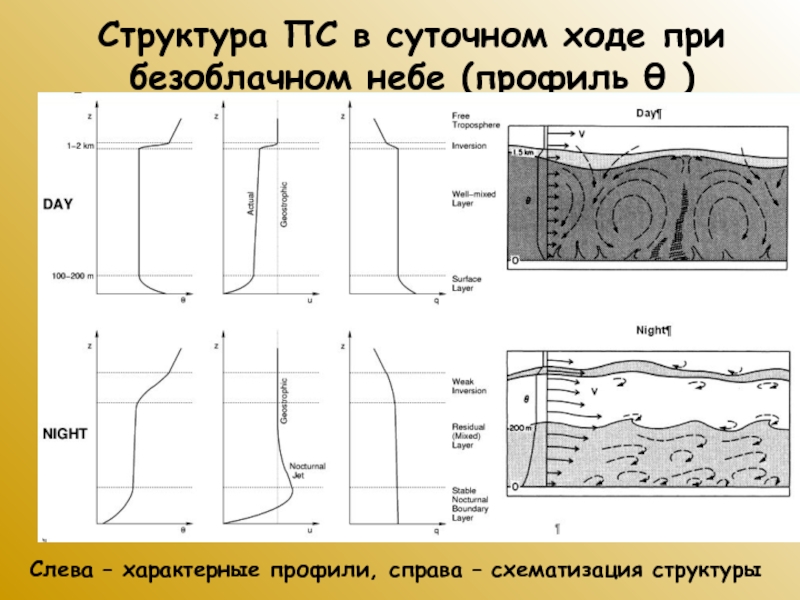
Слайд 10Структура ПС в суточном ходе при безоблачном небе (профиль θ
)
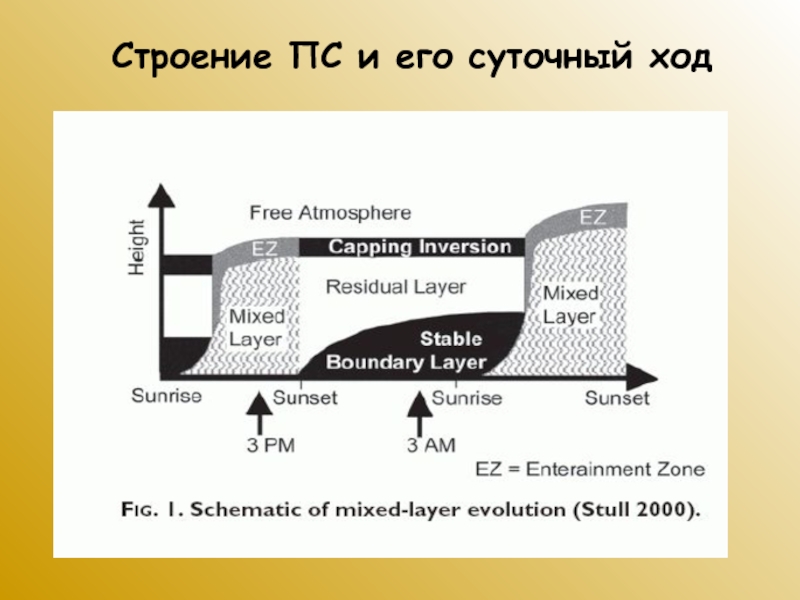
Слева – характерные профили, справа – схематизация структуры
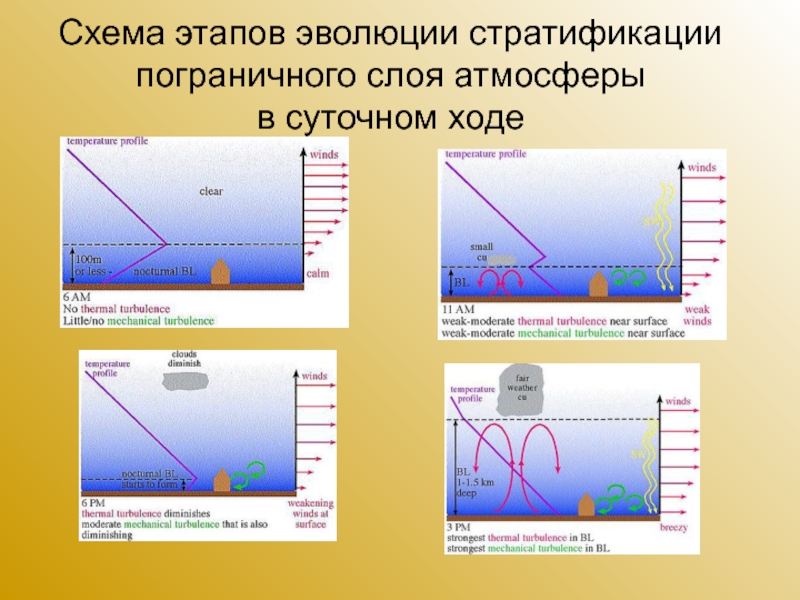
Слайд 11Схема этапов эволюции стратификации пограничного слоя атмосферы
в суточном ходе
Слайд 13Изменения амплитуды суточного хода температуры с высотой. Тепловой ПС
Градиент температуры
у поверхности (0,1 град/м) в сотни раз больше, чем в
тропосфере (0,006 град/м)
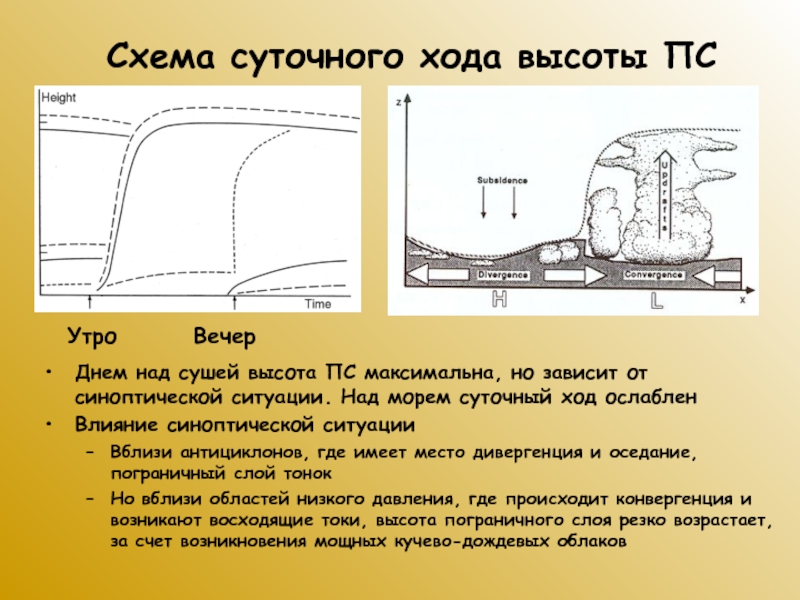
Слайд 14Схема суточного хода высоты ПС
Днем над сушей высота ПС максимальна,
но зависит от синоптической ситуации. Над морем суточный ход ослаблен
Влияние
синоптической ситуации
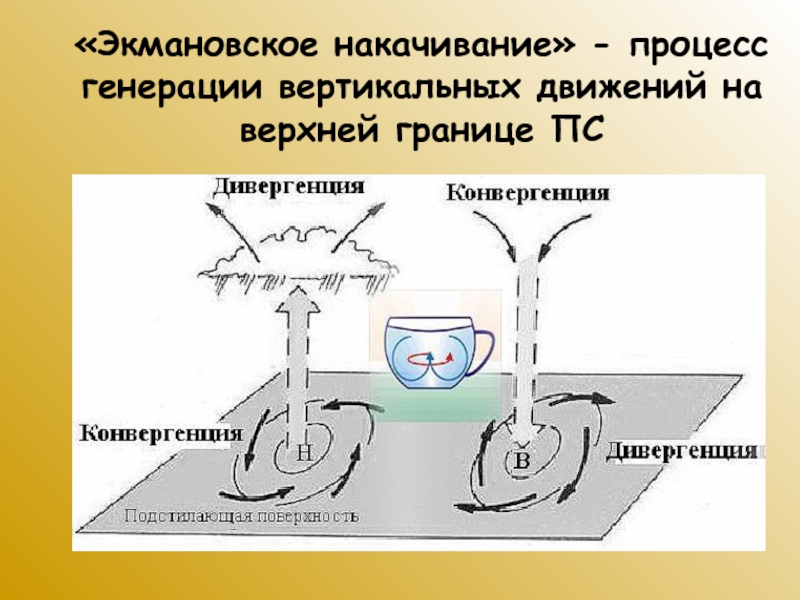
Вблизи антициклонов, где имеет место дивергенция и оседание, пограничный слой тонок
Но вблизи областей низкого давления, где происходит конвергенция и возникают восходящие токи, высота пограничного слоя резко возрастает, за счет возникновения мощных кучево-дождевых облаков
Утро
Вечер
Слайд 15Турбулентность
явление, заключающееся в том, что при увеличении скорости течения жидкости
или газа в среде самопроизвольно образуются многочисленные возмущения различных размеров
без наличия внешних.
экспериментально открыта Рейнольдсомэкспериментально открыта Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах.
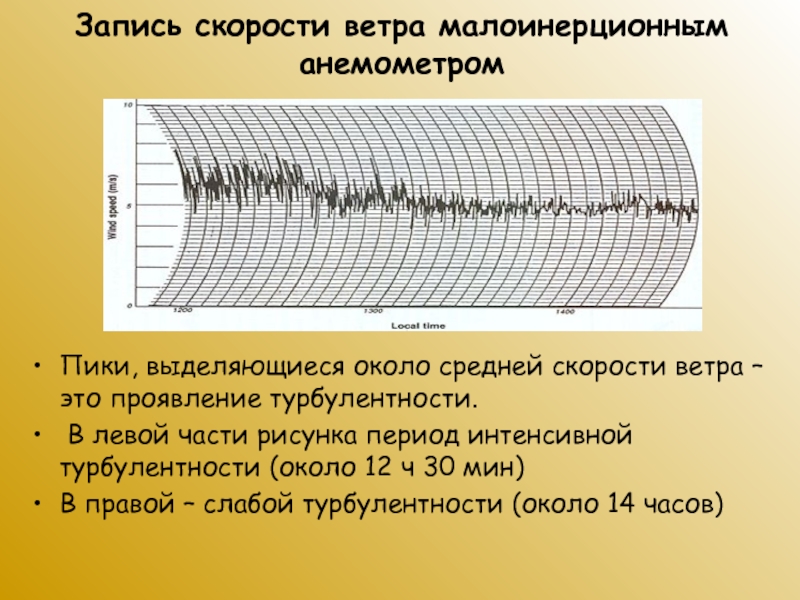
Слайд 16Запись скорости ветра малоинерционным анемометром
Пики, выделяющиеся около средней скорости ветра
– это проявление турбулентности.
В левой части рисунка период интенсивной
турбулентности (около 12 ч 30 мин)
В правой – слабой турбулентности (около 14 часов)
Слайд 17Понятие «турбулентный поток»
Осборн Рейнольдс
Жозеф Буссинеск
Слайд 18Динамическая неустойчивость при сдвиге скорости – причина динамической турбулентности
Развитие турбулентности
в противотоке двух слоев жидкости
Верхний слой более легкой жидкости движется
вправо
Нижний слой более тяжелой жидкости движется влево
На границе слое имеется сдвиг скорости
Волны на границе оказываются неустойчивыми (неустойчивость Кельвина-Гельмгольца)
Они растут
Затем опрокидываются, образуя вихри
С течением времени опрокидывающиеся волны заполняют вихрями область границы
Образуется турбулентный слой
Слайд 20Вторичная неустойчивость на вогнутой стенке
Слайд 21Причины турбулентности в ПС. 1 сдвиг скорости.Число Рейнольдса
Граница с вязкм
подслоем испытывает сильный сдвиг скорости, поэтому там развивается неустойчивость потока.
Это главная причина турбулентности.
Атмосфера всегда турбулентна!
Слайд 22Причины турбулентности в ПС. 2
В дневное время подстилающая поверхность оказывается
сильно нагретой. От нее развивается конвекция. Это вторая причина турбулентности.
Дж.У.Реллей
установил, что критерий возникновения конвекции в слое жидкости толщиной h между двумя плоскостями с разностью температур dT имеет вид Ra = gβh3 dT/χν, где g — ускорение силы тяжести, b — коэффициент теплового расширения жидкости, χν — коэффициенты её вязкости и температуропроводности. Критическое число Рэлея Rakp имеет значение около 1100—1700.
Джордж Уильям Релей
Слайд 23Смысл и определение числа Реллея (Грасгофа)
Если у кубик со стороной
более 1 см перегреть границы на 0.1К, то в нем
начнется конвекция
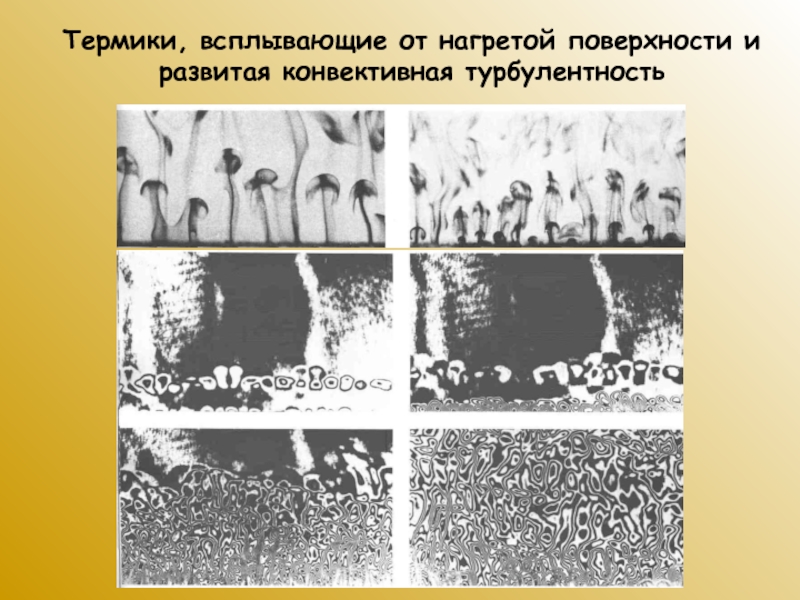
Слайд 24Термики, всплывающие от нагретой поверхности и развитая конвективная турбулентность
Слайд 25
Теория Прандтля для НЕстратифицированного пристенного слоя:
Он указал, что для градиента
скорости течения любой турбулентной жидкости вблизи стенки влияющими параметрами являются:
значение касательного напряжения в пристеночном слое τ,
плотность жидкости ρ,
расстояние до стенки z
(А вязкость несущественна!)
В результате была доказана теорема о логарифмичности профиля скорости
Людвиг Прандтль в 1904 году ввел понятия «пограничный слой» и «основной поток»
Слайд 26Число Ричадсона определяет действие стратификации на турбулентность
Льюис Фрай Ричардсон,
Математик, метеоролог,
психолог. Основоположник численных прогнозов погоды
Значения от 1 до 10 –
типичны для устойчивости. Если меньше 0,1, то в потоке преобладает термическая конвекция. Интервал от 0,1 до 0,25 – переходный от неустойчивости к устойчивости.
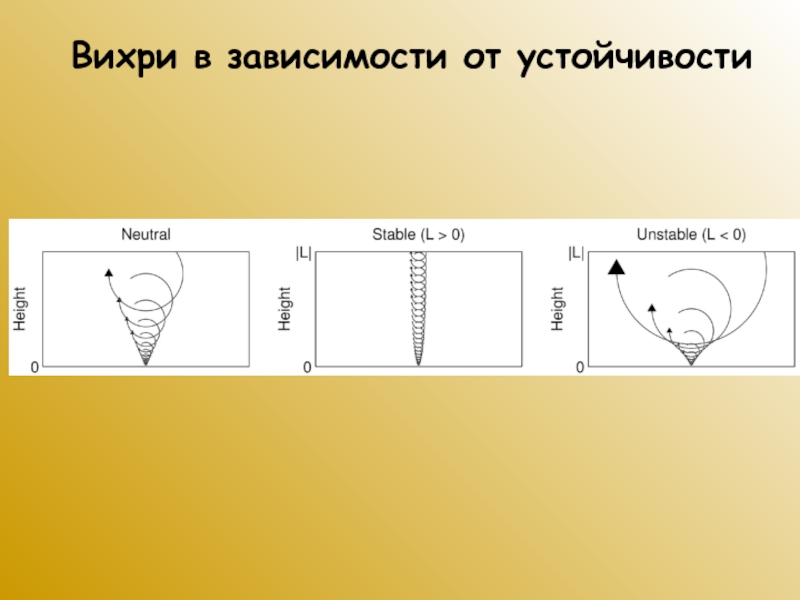
Слайд 27Вихри в зависимости от устойчивости
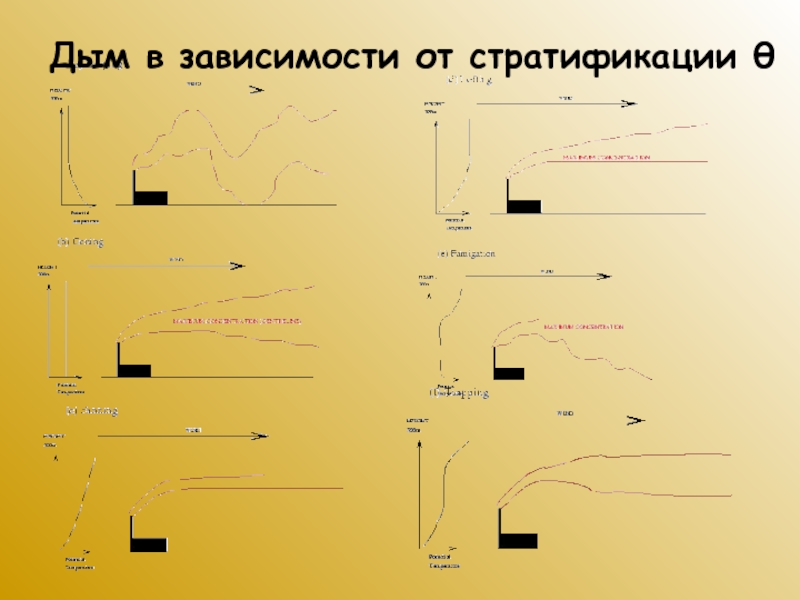
Слайд 28Дым в зависимости от стратификации θ
Слайд 29Как возникает критерий устойчивости Ri>¼
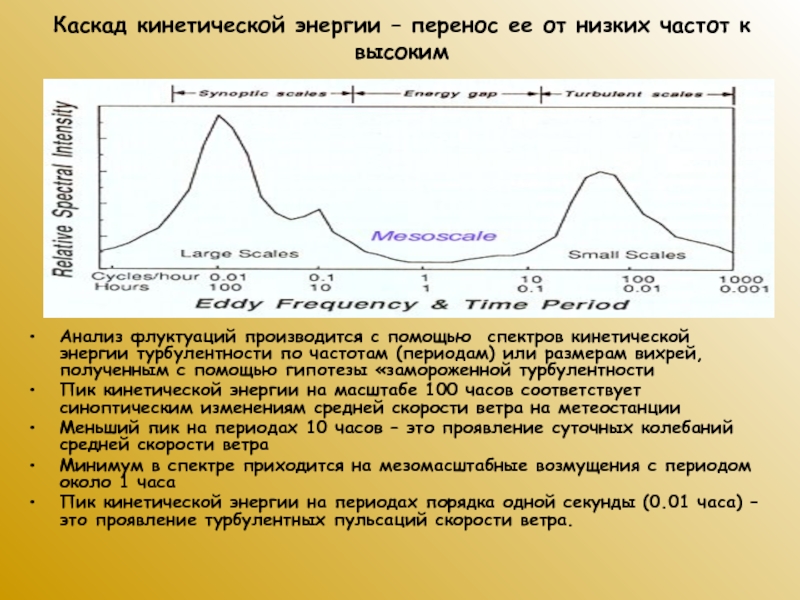
Слайд 30Каскад кинетической энергии – перенос ее от низких частот к
высоким
Анализ флуктуаций производится с помощью спектров кинетической энергии турбулентности по
частотам (периодам) или размерам вихрей, полученным с помощью гипотезы «замороженной турбулентности
Пик кинетической энергии на масштабе 100 часов соответствует синоптическим изменениям средней скорости ветра на метеостанции
Меньший пик на периодах 10 часов – это проявление суточных колебаний средней скорости ветра
Минимум в спектре приходится на мезомасштабные возмущения с периодом около 1 часа
Пик кинетической энергии на периодах порядка одной секунды (0.01 часа) – это проявление турбулентных пульсаций скорости ветра.
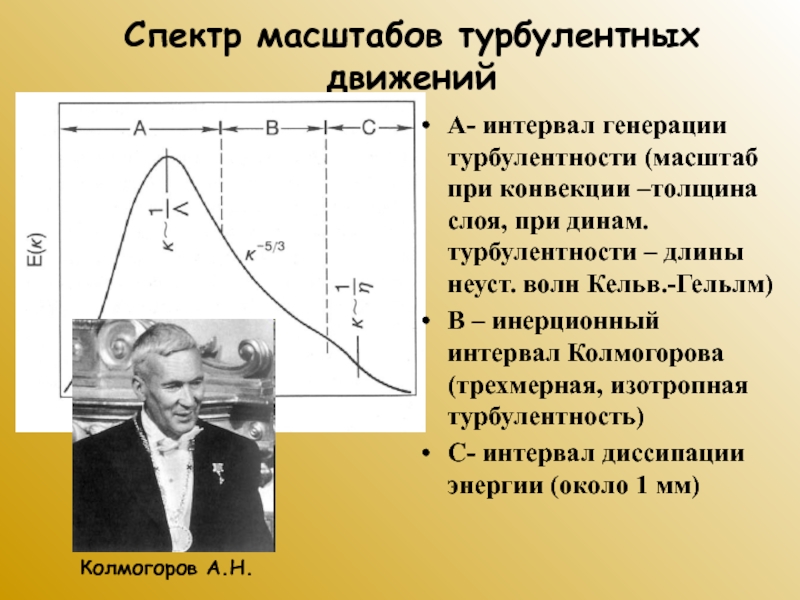
Слайд 31Спектр масштабов турбулентных движений
A- интервал генерации турбулентности (масштаб при конвекции
–толщина слоя, при динам. турбулентности – длины неуст. волн Кельв.-Гельлм)
B
– инерционный интервал Колмогорова (трехмерная, изотропная турбулентность)
C- интервал диссипации энергии (около 1 мм)
Колмогоров А.Н.
Слайд 33Усреднение Рейнольдса 1 для вектора ускорений
Слайд 36Приближение Буссинеска для выявления влияния силы Архимеда
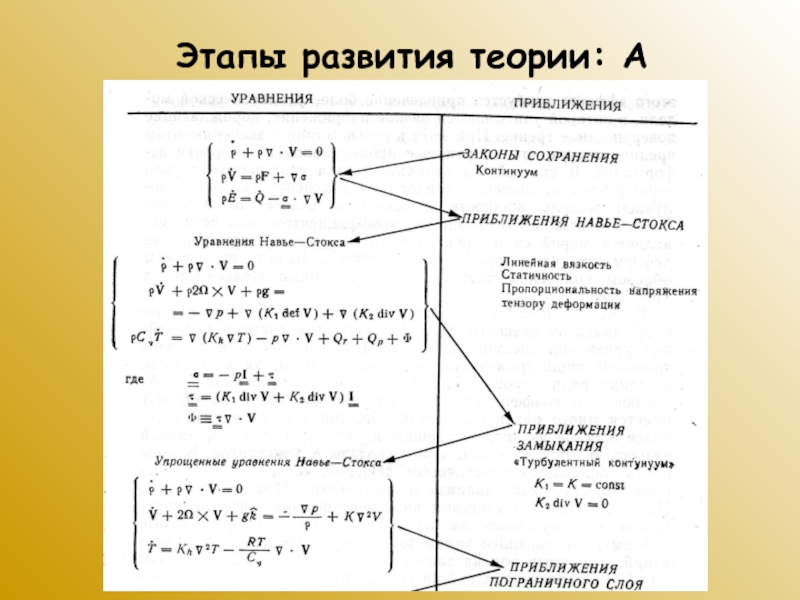
Слайд 37Уравнение динамики в турбулентной атмосфере в приближении Буссинеска. Тензор поверхностных
сил (турбулентных напряжений)
Турбулентная атмосфера– это новая сплошная среда со
своими реолоическими свойствами
Слайд 38Проблема замыкания и уравнения Фридмана-Келлера
В уравнениях Рейнольдса имеется девять компонент
тензора напряжений, которые нужно выразить через средние значения для замыкания
задачи
Самый корректный способ это сделать – составить цепочку уравнений для моментов – уравнений Фридмана-Келлера.
Примером такого подхода является уравнение баланса энергии турбулентности.
А.А. Фридман
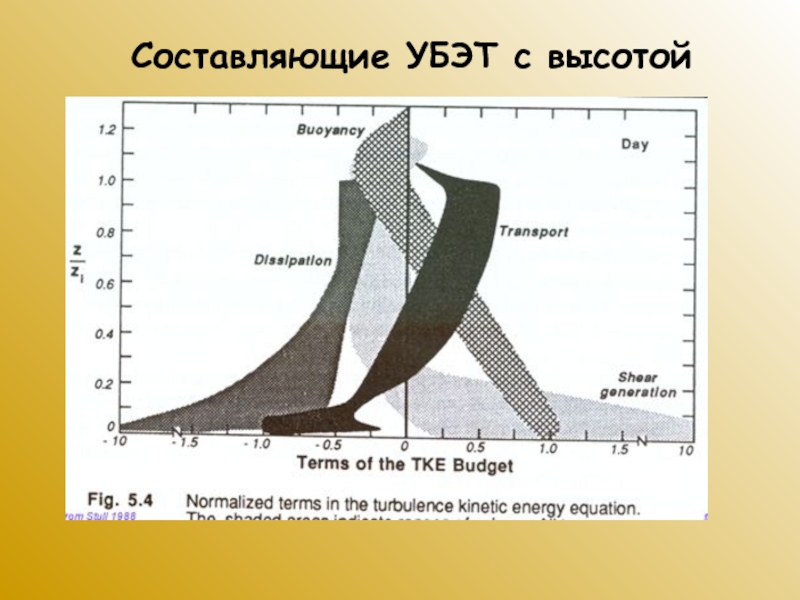
Слайд 39Уравнение баланса энергии турбулентности (УБЭТ) - вывод
Слайд 40Преобразование слагаемых УБЭТ. 1
Слайд 41Преобразование слагаемых УБЭТ. 2
Слайд 44Упрощения уравнений для пограничного слоя атмосферы
Слайд 45Решение проблемы замыкания – простейший вариант
Слайд 46УБЭТ: простейший расчет коэффициента турбулентности
Слайд 47Рабочая формула для оценки постоянного по ПС коэффициента К
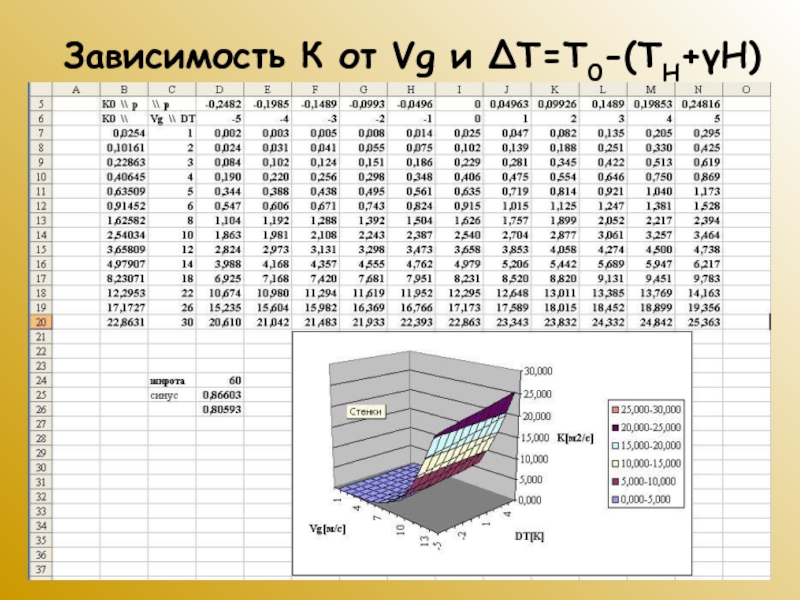
Слайд 48Зависимость К от Vg и ΔT=Т0-(ТH+γH)
Слайд 49Вагн Вильфред Экман (1874-1954)
Швед
Ученик В.Бьеркнеса
Объяснил наблюдавшийся Нансеном на «Фраме»
поворот течения воды с глубиной в работе, выполненной в 1905
г
Слайд 51Спираль Экмана
Используя верхнее граничное условия, получим, что
С1=0, а
С2= ug – i vg .
Разделяя вещественную и мнимую
часть в результате, можно получить зависимости составляющих скорости от высоты при заданном геострофическом ветре в виде:
(
Слайд 52Оценка и смысл a
Коэффициент a имеет размерность обратную длине
Он показывает
на какую высоту нужно подняться, чтобы скорость ветра уменьшилась в
е (примерно 2.7) раз
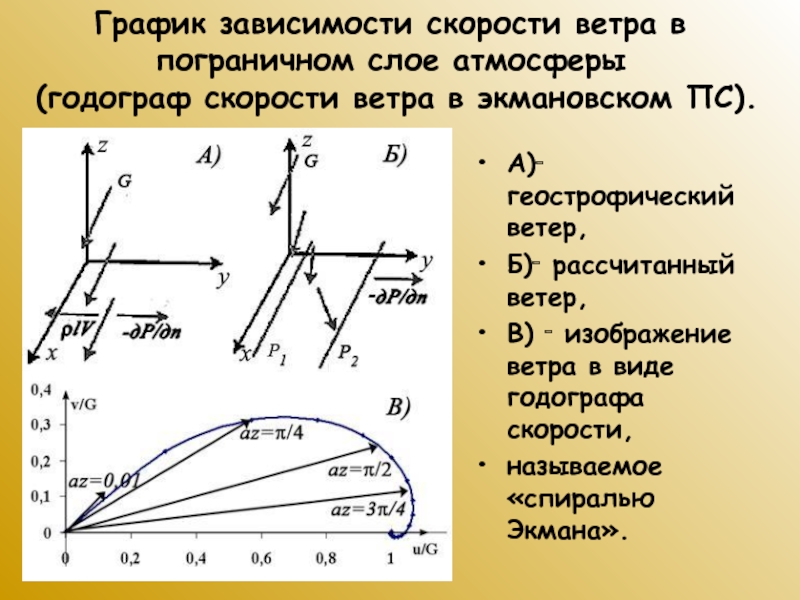
Слайд 53График зависимости скорости ветра в пограничном слое атмосферы
(годограф скорости
ветра в экмановском ПС).
А)‑ геострофический ветер,
Б)‑ рассчитанный ветер,
В)
‑ изображение ветра в виде годографа скорости,
называемое «спиралью Экмана».
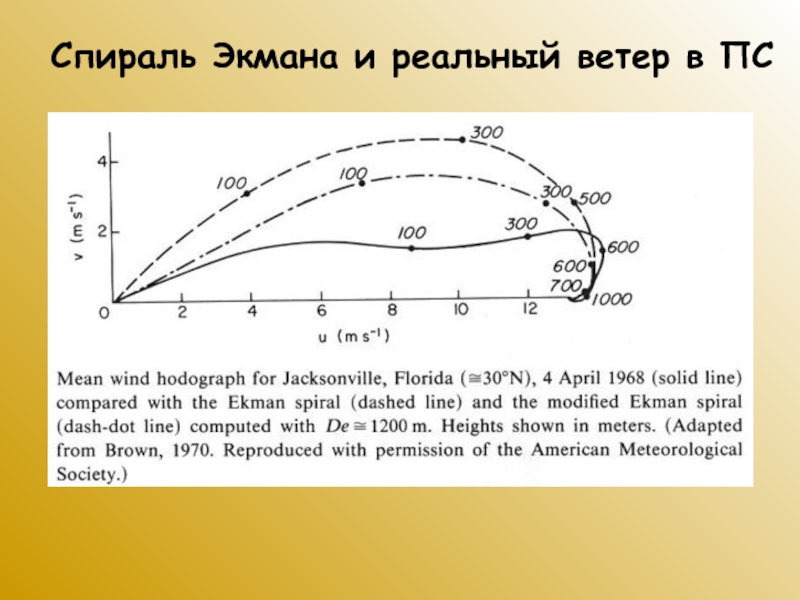
Слайд 54Спираль Экмана и реальный ветер в ПС
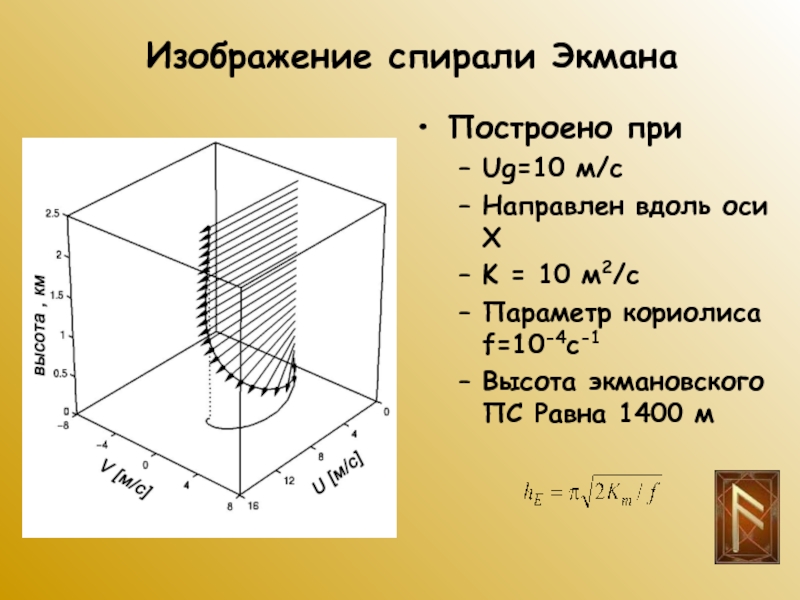
Слайд 55Изображение спирали Экмана
Построено при
Ug=10 м/с
Направлен вдоль оси Х
K =
10 м2/с
Параметр кориолиса f=10-4с-1
Высота экмановского ПС Равна 1400 м
Слайд 56ЧИСЛОВЫЕ ОЦЕНКИ
Ветер совпадет с геострофическим по направлению, если
Sin(aH)=0, т.е. aH=π
или H= π/a
Н – высота экмановского погран.слоя
Если Н≅ 1000 м,
то a=3,110-3м-1, тогда
K=2ωsinϕ/2a2≅7,5 м2/с
Сдвиг ветра δU/δz≅Ug/H=(10м/с)/1000м
Сила трения K δ2U/δz2≅7,510-5 м/с2, т.е. одного порядка с силой Кориолиса и силой барического градиента.
Слайд 57Основные свойства ветра в пограничном слое атмосферы
Первым свойством можно
считать то, что направление ветра начинает совпадать с направлением геострофического
ветра на высоте, определяемой равенством
Второе свойство спирали Экмана касается угла между направлением ветра у земли и направлением геострофического ветра. Этот угол легко найти и оценить по формуле:
Слайд 58Направление действия силы трения:
Направление вектора ветра НЕ точно противоположно вектору
силы трения.
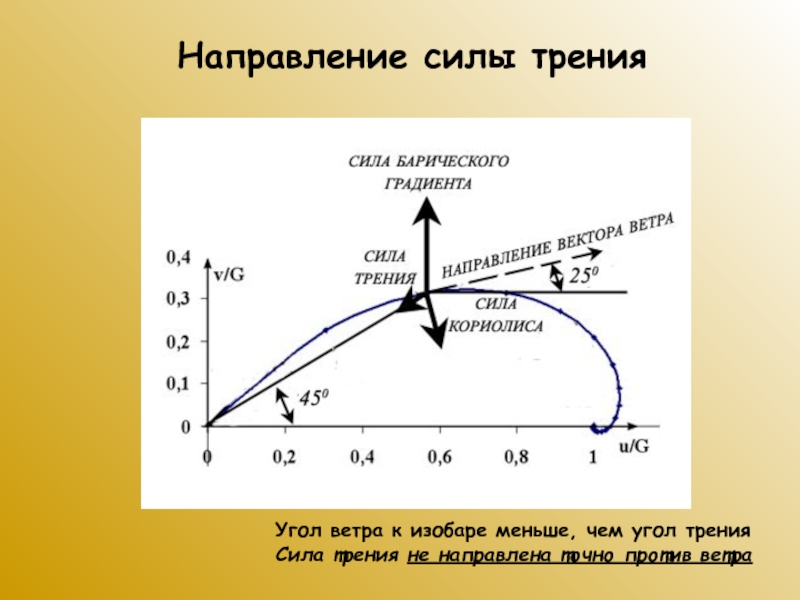
Слайд 59Направление силы трения
Угол ветра к изобаре меньше, чем угол трения
Сила
трения не направлена точно против ветра
Слайд 60Вертикальная скорость на верхней границе экмановского ПС
Третье свойство определяет
вертикальную скорость в экмановском пограничном слое как функцию высоты и
геострофического вихря скорости в виде:
Пример: при Ωg=310-5c-1 (слаб. Ц), a=310-3м-1 оценка w= 1 см/с
Слайд 61«Экмановское накачивание» - процесс генерации вертикальных движений на верхней границе
ПС
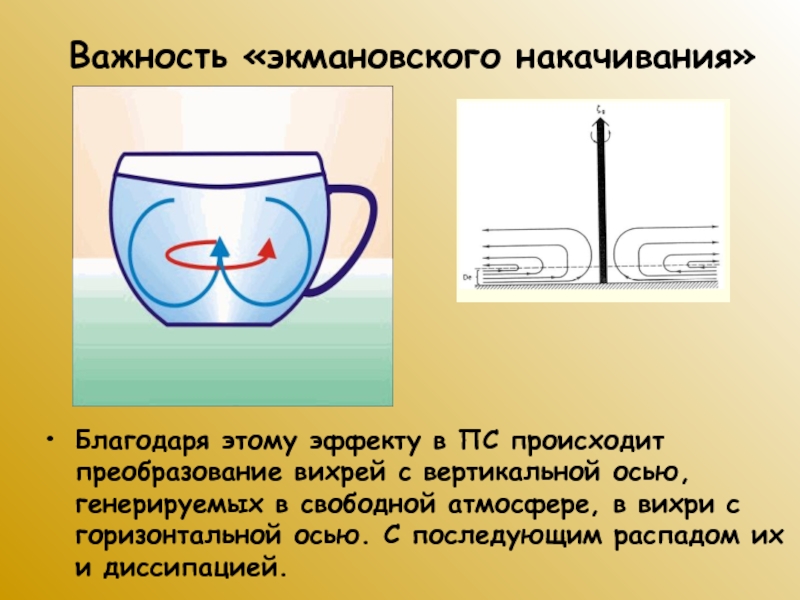
Слайд 62Важность «экмановского накачивания»
Благодаря этому эффекту в ПС происходит преобразование вихрей
с вертикальной осью, генерируемых в свободной атмосфере, в вихри с
горизонтальной осью. С последующим распадом их и диссипацией.
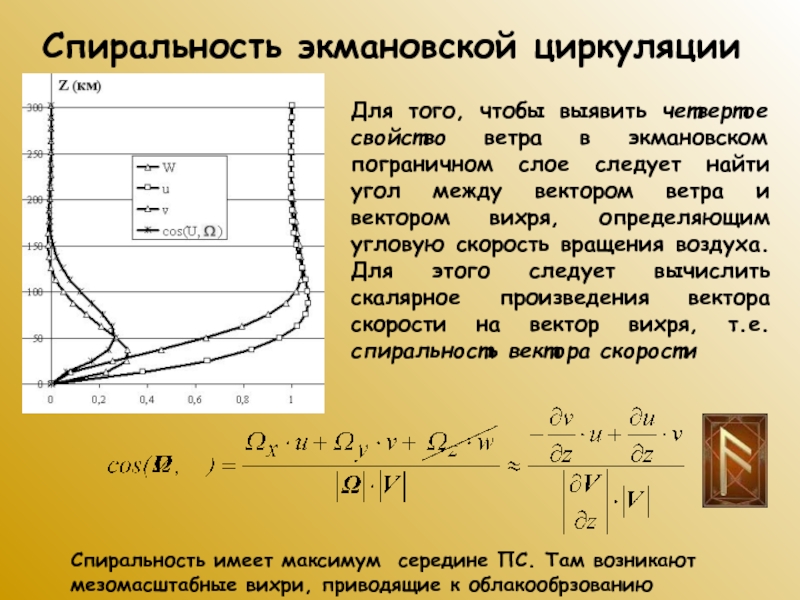
Слайд 63Спиральность экмановской циркуляции
Для того, чтобы выявить четвертое свойство ветра в
экмановском пограничном слое следует найти угол между вектором ветра и
вектором вихря, определяющим угловую скорость вращения воздуха. Для этого следует вычислить скалярное произведения вектора скорости на вектор вихря, т.е. спиральность вектора скорости
Спиральность имеет максимум середине ПС. Там возникают мезомасштабные вихри, приводящие к облакообрзованию