Динамика систем с конечным числом степеней свободы масс

= nθ + nΔ

Для неточечных
масс

С помощью шарнирной
системы

nθ = 2
nΔ =

?

а) без учёта продольных
деформаций стержней

б) с учётом продольных
деформаций стержней

nΔ = 5

nΔ = 8

n = 7

n = 10

nθ =

nнт.м.– для плоской
системы

3nнт.м.– для прост-
ранственной
системы

nнт.м.– количество неточеч-
ных масс

nΔ =

2nм – для плоской
системы

3nм – для простран-
ственной
системы

nм– количество сосре-
доточенных масс

рабочие гипотезы –
( в рамках линейной теории динамических расчётов

):

Рассматриваются линейно деформируемые системы.
Массы сосредоточенные, элементы системы невесомые.
3. Сопротивление внешней среды и внутреннее трение в системе
учитываются по модели вязкого трения.
4. Исследуется движение системы относительно её исходного состояния,
в качестве которого принимается состояние равновесия,
вызванное статическими воздействиями.
5. Определению подлежат динамические составляющие
напряжённо-деформированного состояния движущейся системы
( перемещения, усилия, напряжения, деформации ).

условно недеформированное ) состояние



Начальное
возмущение









F0

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По принципу
Д’Аламбера

FD,i (t)

FD,n (t)

FD,1 (t)

С учётом внешнего и внутреннего трения
( FD (t) – силы сопротивления )

На основании
принципа
суперпозиции:

От инерцион-ных силовых
факторов J(t)

От сил сопротив-
ления FD (t)

FD,k (t)

δik – перемещение в заданной системе
по направлению Ji от Jk = 1 (FD,k = 1)

Направ-
ление Ji

δik

Jk = 1

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По принципу
Д’Аламбера

FD,i (t)

FD,n (t)

FD,1 (t)

С учётом внешнего и внутреннего трения
( FD (t) – силы сопротивления )

FD,k (t)

δik – перемещение в заданной системе
по направлению Ji от Jk = 1 (FD,k = 1)

Направ-
ление Ji

δik

Jk = 1

Ji (t)

FD,i (t)

Ri (t)

Другой способ
вывода уравнений:

момент движения
( t )
yi (t)
yk (t)
yn-1 (t)
y1 (t)
y2 (t)



По принципу
Д’Аламбера
С

учётом внешнего и внутреннего трения
( FD (t) – силы сопротивления )

δik – перемещение в заданной системе
по направлению Ji от

Направ-
ление Ji

δik

Jk = 1

Ji (t)

FD,i (t)

Ri (t)

Другой способ
вывода уравнений:

yn (t)

Rk (t)

Rn (t)

Rn-1 (t)

R1 (t)

R2 (t)

Jk = 1 (FD,k = 1)

Rk = 1

Rk = 1

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

FD,i (t)

FD,n (t)

FD,1 (t)

С учётом внешнего и внутреннего трения
( FD (t) – силы сопротивления )

FD,k (t)

Направ-
ление Ji

δik

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

По модели Фойгта
( вязкого сопротивления ):

δik – перемещение в заданной системе
по направлению Ji от

Jk = 1

Jk = 1

Дифференциальные уравнения
свободного движения системы
с конечным числом степеней свободы масс

( с учётом вязкого сопротивления )

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

FD,i (t)

FD,n (t)

FD,1 (t)

С учетом внешнего и внутреннего трения
( RD (t) – силы сопротивления )

FD,k (t)

Направ-
ление Ji

δik

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

По модели Фойгта
( вязкого сопротивления ):

δik – перемещение в заданной системе
по направлению Ji от

Jk = 1

Jk = 1

( с учётом вязкого сопротивления )

Решение системы
дифференциальных
уравнений:

Дифференциальные уравнения
свободного движения системы
с конечным числом степеней свободы масс

Aij , ϕ0j – из начальных
условий движения

ωj – из дополнительного
( характеристического )
уравнения

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

FD,i (t)

FD,n (t)

FD,1 (t)

FD,k (t)

Направ-
ление Ji

δik

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

δik – перемещение в заданной системе
по направлению Ji от

Jk = 1

Jk = 1

( с учётом вязкого сопротивления )

Решение системы
дифференциальных
уравнений:

Дифференциальные уравнения
свободного движения системы
с конечным числом степеней свободы масс

Aij , ϕ0j – из начальных
условий движения

ωj – из дополнительного
( характеристического )
уравнения

Частный случай –
пренебрежимо малое
сопротивление ( kf 0 )

( без учёта сопротивления )

Полигармоническое движение

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

Решение системы
дифференциальных
уравнений:

Дифференциальные уравнения
свободного движения системы
с конечным числом степеней свободы масс

Aij , ϕ0j – из начальных
условий движения

ωj – из дополнительного
( характеристического )
уравнения

Частный случай –
пренебрежимо малое
сопротивление ( kf 0 )

( без учёта сопротивления )

Полигармоническое движение

0

t

yi (t)

Частный случай –
собственные
колебания

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

Решение системы
дифференциальных
уравнений:

Aij , ϕ0j – из начальных
условий движения

ωj – из дополнительного
( характеристического )
уравнения

Частный случай –
собственные
колебания

– по определению собственных
колебаний

0

t

yi (t), yk(t)

yi

yi

yk

yk

Ускорение:

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

Решение системы
дифференциальных
уравнений:

Частный случай –
собственные
колебания

– по определению собственных
колебаний

0

t

yi (t), yk(t)

yi

yi

yk

yk

Уравнения движения масс при собственных
колебаниях системы с конечным числом n

ϕ(t) = ωj t + ϕ0j – фаза колебаний

При произвольном t sin ϕ(t) = 0

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

Решение системы
дифференциальных
уравнений:

Частный случай –
собственные
колебания

– по определению собственных
колебаний

0

t

yi (t), yk(t)

yi

yi

yk

yk

Уравнения движения масс при собственных
колебаниях системы с конечным числом n

ϕ(t) = ωj t + ϕ0j – фаза колебаний

При произвольном t sin ϕ(t) = 0

Уравнения собственных колебаний
системы с конечным числом n
( в амплитудах перемещений масс )

момент движения
( t )
Ji (t)






yi (t)
yk (t)
yn (t)
yn-1 (t)
y1 (t)
y2

(t)

Jn (t)

J1 (t)

J2 (t)

Jk (t)

Jn-1 (t)

По закону инерции:

– если yk(t) – линейное
перемещение массы

– если yk(t) – угол по-
ворота неточечной
массы

Частный случай –
собственные
колебания

Уравнения собственных колебаний
системы с конечным числом n
( в амплитудах перемещений масс )

Амплитудное
состояние системы

yi

yk

yn

y1

y2

yn-1

J1

J2

Ji

Jk

Jn

Jn-1

Инерционный фактор Jk(t)
направлен в ту же сторону,
что и перемещение yk(t)

инерции:
– если yk(t) – линейное
перемещение массы
– если yk(t)

– угол по-
ворота неточечной
массы

Частный случай –
собственные
колебания

Уравнения собственных колебаний
системы с конечным числом n
( в амплитудах перемещений масс )

Амплитудное
состояние системы

yi

yk

yn

y1

y2

yn-1

J1

J2

Ji

Jk

Jn

Jn-1

Уравнения собственных колебаний системы с конечным числом n
( в амплитудах перемещений масс )

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Инерционный фактор Jk(t)
направлен в ту же сторону,
что и перемещение yk(t)

инерции:
– если yk(t) – линейное
перемещение массы
– если yk(t)

– угол по-
ворота неточечной
массы

Частный случай –
собственные
колебания

Амплитудное
состояние системы

yi

yk

yn

y1

y2

yn-1

J1

J2

Ji

Jk

Jn

Jn-1

Уравнения собственных колебаний системы с конечным числом n
( в амплитудах перемещений масс )

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

( в амплитудах инерционных силовых факторов )

Инерционный фактор Jk(t)
направлен в ту же сторону,
что и перемещение yk(t)

инерции:
– если yk(t) – линейное
перемещение массы
– если yk(t)

– угол по-
ворота неточечной
массы

Частный случай –
собственные
колебания

Амплитудное
состояние системы

yi

yk

yn

y1

y2

yn-1

J1

J2

Ji

Jk

Jn

Jn-1

Уравнения собственных колебаний системы с конечным числом n

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

( в амплитудах инерционных силовых факторов )

Инерционный фактор Jk(t)
направлен в ту же сторону,
что и перемещение yk(t)

свободного движения – собственные колебания
Уравнения собственных колебаний системы с конечным

числом n

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

а) в амплитудах перемещений масс:

б) в амплитудах инерционных
силовых факторов:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

системы с конечным числом n
. . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

в амплитудах инерционных силовых факторов ( сил инерции ):

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В матричной форме:

– вектор
амплитуд
инерцион-
ных сил

– матрица дина-
мической подат-
ливости системы
по направлениям
инерционных сил

В матричной форме:

– вектор
амплитуд
инерцион-
ных сил

– матрица дина-
мической подат-
ливости системы
по направлениям
инерционных сил

системы с конечным числом n
в амплитудах инерционных силовых факторов (

сил инерции ):

В матричной форме:

– вектор
амплитуд
инерцион-
ных сил

– матрица дина-
мической подат-
ливости системы
по направлениям
инерционных сил

δ – матрица
упругой податливости системы по направлениям
инерционных сил

матрица динамических ( инерционных ) поправок к податливости системы

матрица масс, порождаю-щих инерционные сило-вые факторы J1, J2 ,…, Jn

Варианты решения уравнений СК

1) J = 0 – тривиальное решение ( отсутствие движения )

2) J = 0 – нетривиальное решение ( условие существования
движения )

уравнений собственных колебаний:


– характеристическое
уравнение
J = 0

(

)

уравнение частот
собственных колебаний

( вековое уравнение, частотное уравнение )

0

λ

λ1

λ2

λj

λn

– собственные значения ( числа )

– спектр частот собственных колебаний
( совокупность частот в порядке их возрастания )

ω1 – частота основного тона колебаний

ω2 ,…, ωn – частоты обертонов

Пример: при n = 2

)
Формы собственных колебаний ( главные формы колебаний )


y1( j)
y2( j)
yi(

j)

yn( j)

Главная форма,
соответствующая
частоте ωj

Вектор амплитуд
перемещений
j-й главной формы

Собственный вектор
перемещений
j-й главной формы

Собственный вектор
инерционных сил
j-й главной формы

)
Формы собственных колебаний ( главные формы колебаний )


y1( j)
y2( j)
yi(

j)

yn( j)

Главная форма,
соответствующая
частоте ωj

Вектор амплитуд
перемещений
j-й главной формы

Собственный вектор
перемещений
j-й главной формы

(δkk – λj /ak)

n уравнений

n – 1 неизвестных

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

n – 1 уравнений

βJ(j)

Свойства главных форм

( главные формы колебаний )


y1( j)
y2( j)
yi( j)
yn( j)
Главная форма,
соответствующая
частоте

ωj

Свойства главных форм

Главные формы колебаний
взаимно ортогональны.

2. Большим частотам из спектра
соответствуют более сложные главные формы ( с большим
числом узлов и пучностей стоячих волн ).

Смысл ортогональности главных форм:
возможная работа инерционных силовых факторов
любой главной формы на перемещениях масс
в другой главной форме равна нулю: Wjs = 0

y1(s)

y2(s)

yi ( s)

yn(s)

Главная форма,
соответствующая
частоте ωs

j, s – номера главных форм

ωs < ωj

J2( j)

J1( j)

Ji( j)

Jn( j)

По теореме Бетти для равновесных состояний j и s :

Wjs – Wsj = 0

Wjs = 0

Выражения условия ортогональности ГФК
через собственные векторы
сил инерции и перемещений:

( главные формы колебаний )


y1( j)
y2( j)
yi( j)
yn( j)
Главная форма,
соответствующая
частоте

ωj

Свойства главных форм

Главные формы колебаний
взаимно ортогональны.

2. Большим частотам из спектра
соответствуют более сложные главные формы ( с большим
числом узлов и пучностей стоячих волн ).

Смысл ортогональности главных форм:
возможная работа инерционных силовых факторов
любой главной формы на перемещениях масс
в другой главной форме равна нулю: Wjs = 0

y1(s)

y2(s)

yi ( s)

yn(s)

Главная форма,
соответствующая
частоте ωs

j, s – номера главных форм

ωs < ωj

J2( j)

J1( j)

Ji( j)

Jn( j)

Выражения условия ортогональности ГФК
через собственные векторы
сил инерции и перемещений:

а)

б)

в)

( главные формы колебаний )




Главные формы, соответствующие частотам
J2(1)





































ω1
ω3
ω2
ω1 < ω2

< ω3

n = 3

J1(1)

J3(1)

J2(2)

J1(2)

J3(2)

J2(2)

J1(2)

J3(2)

( главные формы колебаний )





n = 3
П р и м

е р

H / 3

H / 3

H / 3

m

3m

4m

Определить частоты и формы собственных колебаний

y1

y2

y3

J1

J2

J3

m

3m

4m

EI

2EI

4EI

J3= 1

J2= 1

J1= 1

δ11

δ12

δ13

δ21

δ22

δ23

δ31

δ32

δ33

2H / 3

H / 3

H

k = 1

k = 2

k = 3

M1

M2

M3

m1 = m

m2 = 3m

m3 = 4m

a = 1 3 4

m0= m

Уравнение частот СК:

( главные формы колебаний )




n = 3
П р и м

е р

H / 3

H / 3

H / 3

Определить частоты и формы собственных колебаний

y1

y2

y3

J1

J2

J3

m

3m

4m

J3= 1

J2= 1

J1= 1

δ11

δ12

δ13

δ21

δ22

δ23

δ31

δ32

δ33

2H / 3

H / 3

H

k = 1

k = 2

k = 3

M1

M2

M3

Уравнение частот СК:

EI

2EI

4EI

( главные формы колебаний )




n = 3
П р и м

е р

H / 3

H / 3

H / 3

Определить частоты и формы собственных колебаний

y1

y2

y3

J1

J2

J3

m

3m

4m

J3= 1

J2= 1

J1= 1

δ11

δ12

δ13

δ21

δ22

δ23

δ31

δ32

δ33

2H / 3

H / 3

H

k = 1

k = 2

k = 3

M1

M2

M3

Уравнение частот СК:

– 0,0833 λ3 + 11,3333 λ2 –
– 99,7497 λ + 124 = 0

λ1 = 126,64; λ2 = 7,865; λ3 = 1,494

EI

2EI

4EI

( главные формы колебаний )




Главные формы, соответствующие частотам
J2(1)





































ω1
ω3
ω2
ω1 < ω2

< ω3

n = 3

0,68J2(1)

0,35J2(1)

0,93J3(2)

0,58J3(2)

J3(2)

0,55J3(3)

0,14J1(3)

J3(3)

y1(1)

0,49y1(1)

0,13y1(1)

y1(2)

0,43y1(2)

0,53y1(2)

0,73y3(3)

0,56y3(3)

y3(3)

Для
башни:

H / 3

H / 3

H / 3

3m

4m

m

H / 10

Для стальной башни высотой Н = 200 м

Проверка ортогональности главных форм:

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 33» )
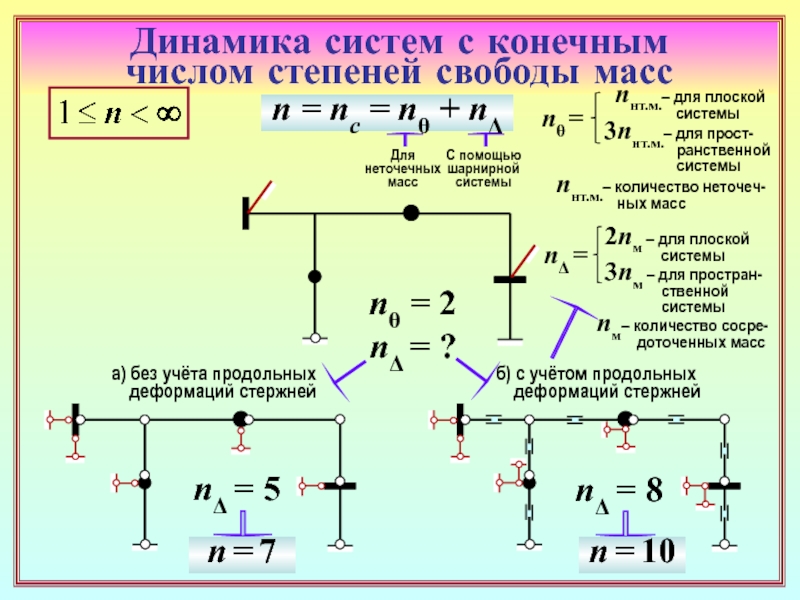
1. Какими должны быть массы системы, чтобы число их степеней свободы n было
конечным? От чего зависит и как определяется число n? ( ( 2( 2 )
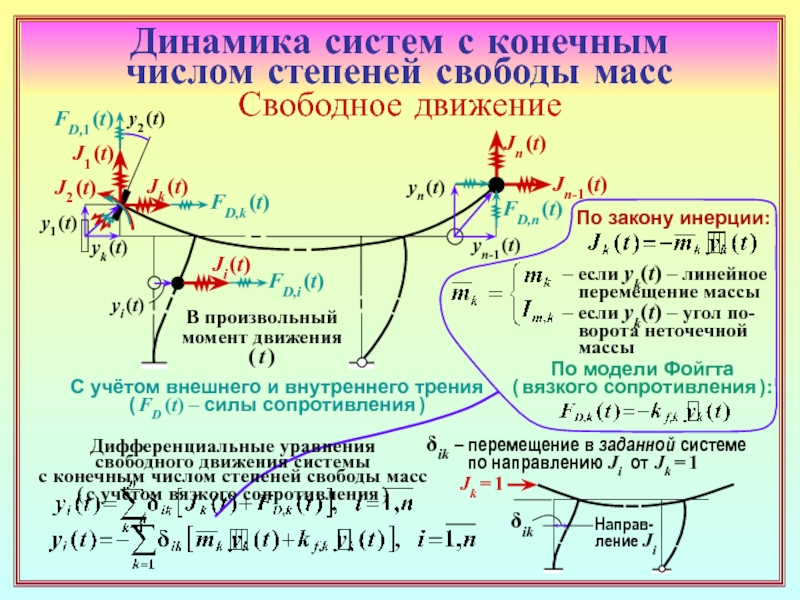
2. Исходные предпосылки и рабочие гипотезы линейной теории расчёта систем с
конечным числом степеней свободы масс (КЧССМ) в случае свободного движения. ( ( 3( 3 )
3. Как при использовании кинетостатического метода формируется расчётная схема
заданной системы при её свободном движении? ( ( 4 – 6 ( 4 – 6 )
4. На описании каких величин строится вывод дифференциальных уравнений
свободного движения масс? ( ( 6( 6 )
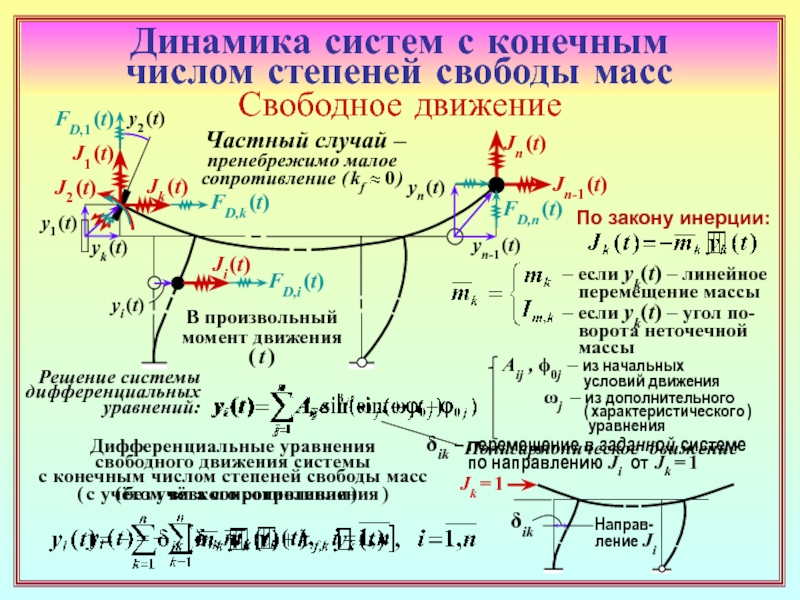
5. Понятие об общем решении системы дифференциальных уравнений свободного
движения с учётом и без учёта сил сопротивления. ( ( 9 – 12 ( 9 – 12 )
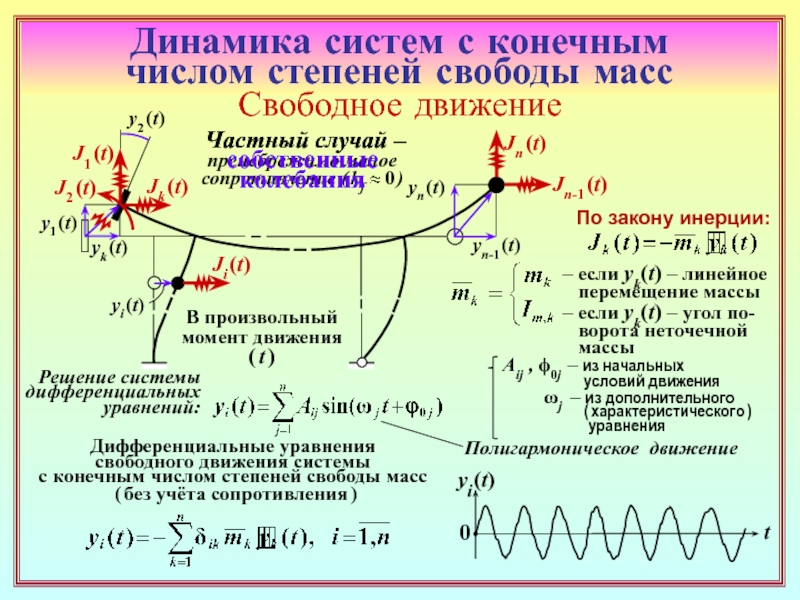
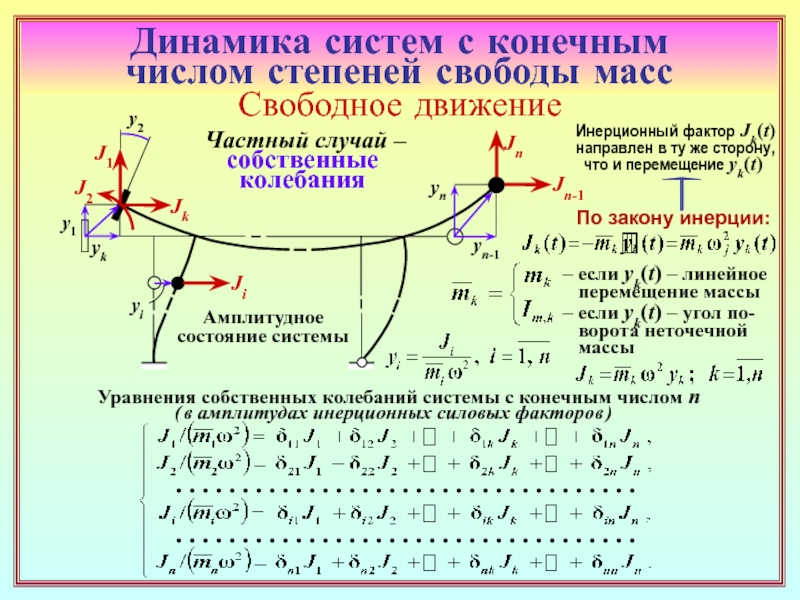
6. Частный случай свободного движения – собственные колебания системы с КЧССМ:
особенности записи закона инерции ( ( 16( 16 ) и уравнений относительно функций
перемещений масс. ( ( 13 – 15 ( 13 – 15 )
7. Какой смысл имеет характеристика массы в зависимости от того, каким является
перемещение yk(t) – линейным или угловым? ( ( 9( 9 )
8. Как соотносятся при собственных колебаниях направления перемещений масс
и соответствующих им инерционных силовых факторов? ( ( 16 ( 16 )
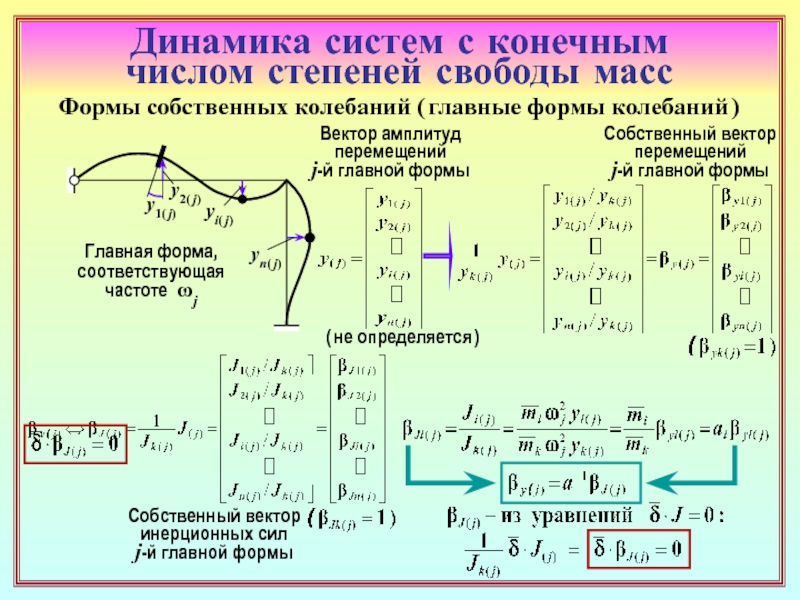
9. Как получаются уравнения собственных колебаний в амплитудах перемещений
масс ( ( 16 – 18 ( 16 – 18 ) и в амплитудах инерционных силовых факторов? ((18 – 19 (18 – 19 )
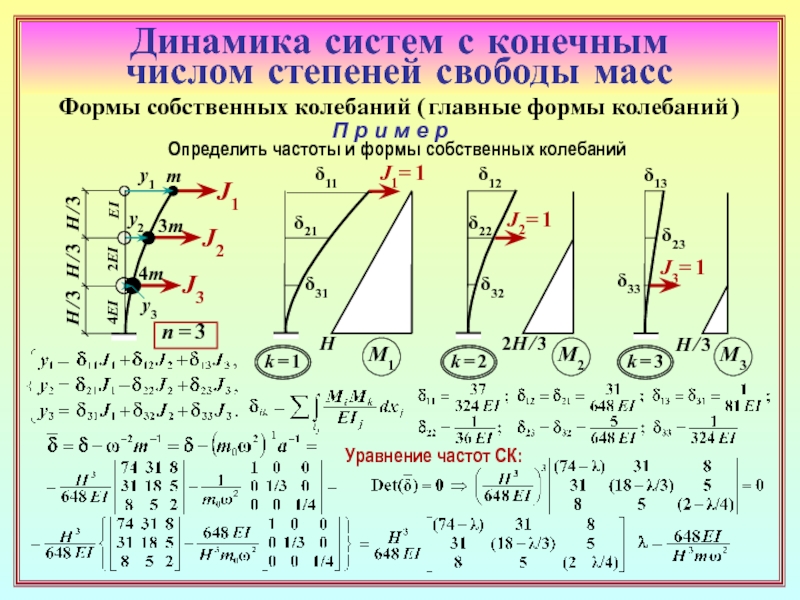
10. Основные ( канонические ) уравнения собственных колебаний системы с конечным
числом степеней свободы в амплитудах перемещений масс ( ( 17 ( 17 ) , ( ( 20 ( 20 ) и инерционных
силовых факторов ( 19, 20 , 20 ), 20 ) , ( , 20 ) , ( 21 , 20 ) , ( 21 ) ; их физический смысл.
11. Что такое матрица динамической податливости системы и какие свойства заданной
системы она отражает? Почему эта матрица является, по существу, комплексной
характеристикой движущейся заданной системы? ( ( 21, 22 ( 21, 22 )
*) Только в режиме «Показ слайдов»

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 34» )
12. Какие существуют варианты решения системы уравнений собственных колебаний? ( 22 )
13. Почему тривиальное решение системы уравнений не представляет интереса?
14. Какое условие ( требование ) используется для получения уравнения частот
собственных колебаний из основных уравнений? ( 23 )
15. Как записывается уравнение частот собственных колебаний системы с конечным
числом степеней свободы? ( 23 )
16. Что называется спектром частот собственных колебаний сооружения? Сколько частот
входит в спектр? ( ( 23 ( 23 ) Как называются первая и последующие частоты? ( ( 23 ( 23 )
17. Какие характеристики системы оказывают наибольшее влияние на частоты
собственных колебаний ( как именно )? – по аналогии с формулой для ω системы с n = 1
18. Как сказываются на частотах собственных колебаний ошибки в опреде-
лении числа степеней свободы масс? Что опаснее – завышение или зани-
жение n в сравнении с истинным? – объяснить.
19. Если в найденном спектре частот собственных колебаний обнаружатся
бесконечно большие значения, то чем это можно объяснить?
20. Почему даже при известной частоте собственных колебаний невозможно
определить числовые значения сил инерции и перемещений масс? – дать
физическое и математическое объяснения.
21. Что такое главные формы колебаний? – см. лекцию 1
22. Основные свойства главных форм. ( ( 26 ( 26 )
23. Каков физический смысл свойства ортогональности главных форм? ( 26 )
24. Варианты записи условия ортогональности главных форм. ( ( 27 ( 27 )
25. Как найти собственные векторы сил инерции и перемещений масс, соответствующие
некоторой частоте собственных колебаний системы? ( ( 24 ( 24 )

*) Только в режиме «Показ слайдов»

см. [ 3 ]
из списка
рекомендуемых
учебно-методи-
ческих изданий

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 35» )

26. Как строятся схемы главных форм колебаний? ( ( 31( 31 ) Что можно использовать для
уточнения этих схем?
27. Как отличить по виду главные формы, соответствующие более высоким
частотам, от низкочастотных форм? ( ( 26 ( 26 )
28. Какое практическое значение имеет знание форм собственных колебаний
сооружения?
29. Каков смысл кинематической проверки результатов расчёта сооружения
на собственные колебания и как она выполняется?
30. Изложить общий алгоритм решения задачи о собственных колебаниях
системы с конечным числом степеней свободы масс.

*) Только в режиме «Показ слайдов»

см. [ 3 ]
из списка
рекомендуемых
учебно-методи-
ческих изданий