Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина : Автоматизированный электрический привод Лекция № 2
Содержание
- 1. Дисциплина : Автоматизированный электрический привод Лекция № 2
- 2. 1. Механические характеристики исполнительных механизмов (ИМ).2. Классификация
- 3. 2Функциональная зависимость между статическим моментом (моментом сопротивления)
- 4. 3 Статические моменты исполнительных механизмов делятся на
- 5. 4 При x=1, механическая характеристика линейно-возрастающая (прямая
- 6. 5 Механической характеристикой ЭД называется зависимость угловой
- 7. 6 В зависимости от того как электродвигатели
- 8. 7Абсолютно жесткая характеристика, для которой Ω =
- 9. 83. Понятие о статической устойчивости работы электроприводаРаботе
- 10. 9Под статической устойчивостью понимается такое состояние установившегося
- 11. 10ЭД при моменте сопротивления Мс =
- 12. 11Пример устойчивой и неустойчивой работы ЭП рассмотрим
- 13. Скачать презентанцию
1. Механические характеристики исполнительных механизмов (ИМ).2. Классификация механических характеристик электродвигателей (ЭД).3. Понятие о статической устойчивости работы электропривода.1ВОПРОСЫЛИТЕРАТУРАМ.Г.Чиликин, А.С.Сандлер «Общий курс электропривода», стр. 32...38.
Слайды и текст этой презентации
Слайд 1Дисциплина:
«Автоматизированный электрический привод»
Лекция № 2:
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИСПОЛНИТЕЛЬНЫХ МЕХАНИЗМОВ И
ЭЛЕКТРОДВИГАТЕЛЕЙ
«ВОЗОБНОВЛЯЕМЫЕ ИСТОЧНИКИ ЭНЕРГИИ И ЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ И СЕТИ»Слайд 21. Механические характеристики исполнительных механизмов (ИМ).
2. Классификация механических характеристик электродвигателей
(ЭД).
3. Понятие о статической устойчивости работы электропривода.
1
ВОПРОСЫ
ЛИТЕРАТУРА
М.Г.Чиликин, А.С.Сандлер
«Общий курс
электропривода», стр. 32...38.Слайд 32
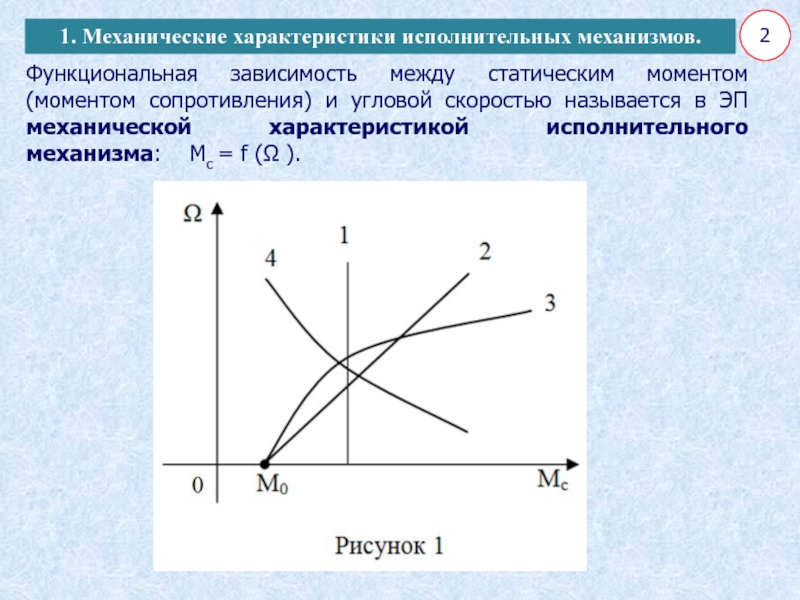
Функциональная зависимость между статическим моментом (моментом сопротивления) и угловой скоростью
называется в ЭП механической характеристикой исполнительного механизма: Mс =
f (Ω ).1. Механические характеристики исполнительных механизмов.
Слайд 43
Статические моменты исполнительных механизмов делятся на 2 класса:
1. Моменты,
не зависящие от параметров движения: Mc = const (для грузоподъемных
механизмов и для поршневых насосов, работающих на постоянное противодавление.2. Моменты, зависящие от скорости: Mc = f(Ω)
Для многих механизмов эта зависимость в общем случае выражается эмпирическим уравнением:
(1)
где: Mс – момент сопротивления производственного механизма при скорости Ω
M0 – начальный статический момент, обусловленный трением,
Mс.н – момент сопротивления при номинальной скорости ΩН,
x – показатель степени, определяющий характер зависимости (–1 ≤ x ≤ 2 ).
Слайд 54
При x=1, механическая характеристика линейно-возрастающая (прямая 2 на рис.
1), момент сопротивления линейно зависит от скорости Ω, увеличиваясь с
ее возрастанием.Ω ↑ → Е↑ → I ↑ → Mэм↑ = Mс↑
При x= 2 механическая характеристика нелинейно-возрастающая (параболическая) (кривая 3 на рис. 1).
При x = –1 механическая характеристика нелинейно – спадающая (кривая 4 на рис.1).
Момент сопротивления МС изменяется обратно пропорционально скорости, а мощность, потребляемая механизмом, остается постоянной Рmax=const .
[Рmax = M ↑ Ω ↓]
Слайд 65
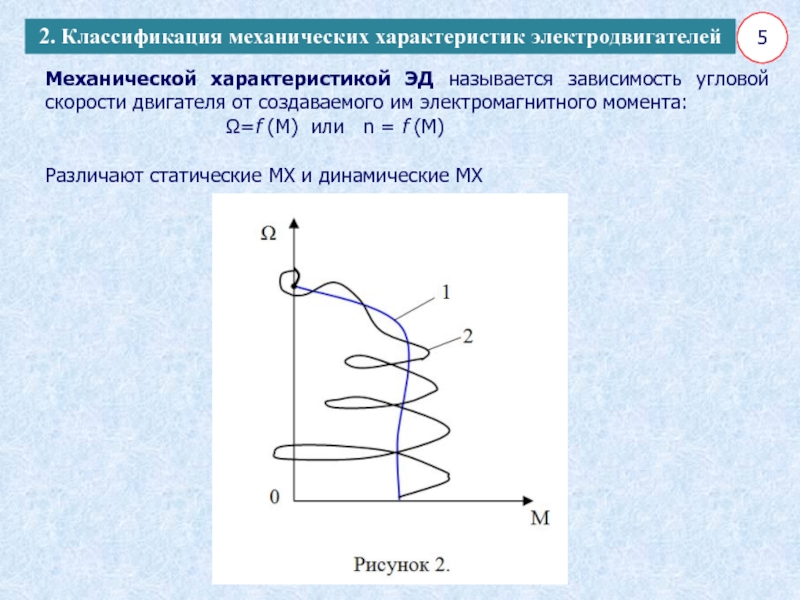
Механической характеристикой ЭД называется зависимость угловой скорости двигателя от
создаваемого им электромагнитного момента:
Ω=f (M) или n = f (M) Различают статические МХ и динамические МХ
2. Классификация механических характеристик электродвигателей
Слайд 76
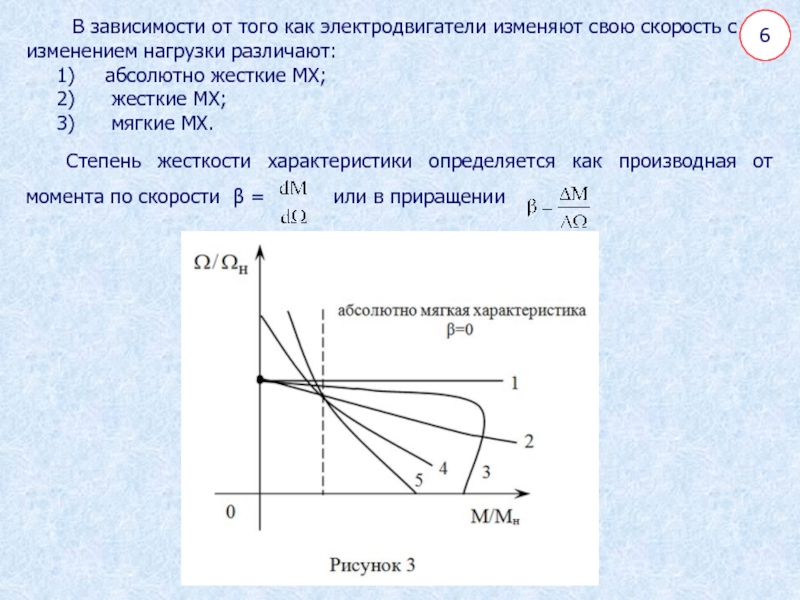
В зависимости от того как электродвигатели изменяют свою скорость
с изменением нагрузки различают:
абсолютно жесткие МХ;
жесткие МХ;
мягкие МХ. Степень жесткости характеристики определяется как производная от момента по скорости β = или в приращении
Слайд 87
Абсолютно жесткая характеристика, для которой
Ω = const, =∞.
Такую характеристику
имеют синхронные электродвигатели (график 1 на рис.3).
Жесткая характеристика, для
которой Ω с ростом М падает незначительно ≥ 10 ÷ 40. На таких характеристиках работают ЭД постоянного тока с независимым и параллельным возбуждением (график 2 на рис.3) и асинхронные двигатели в пределах допустимых нагрузок (график 3 на рис.3).
Мягкая характеристика для которой < 10. К таким характеристикам относятся характеристики ЭД постоянного тока со смешанным (график 4 на рис. 3) и последовательным возбуждением (график 5 на рис. 3).
Крайний случай мягкой характеристики это когда при Ω = var Mc= сonst и β = 0 .
Слайд 98
3. Понятие о статической устойчивости работы электропривода
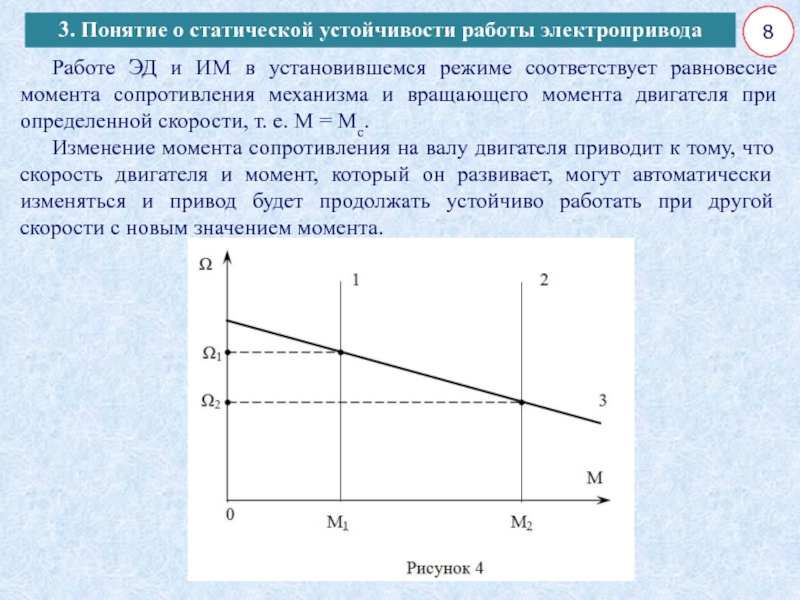
Работе ЭД и ИМ
в установившемся режиме соответствует равновесие момента сопротивления механизма и вращающего
момента двигателя при определенной скорости, т. е. M = Mс.Изменение момента сопротивления на валу двигателя приводит к тому, что скорость двигателя и момент, который он развивает, могут автоматически изменяться и привод будет продолжать устойчиво работать при другой скорости с новым значением момента.
Слайд 109
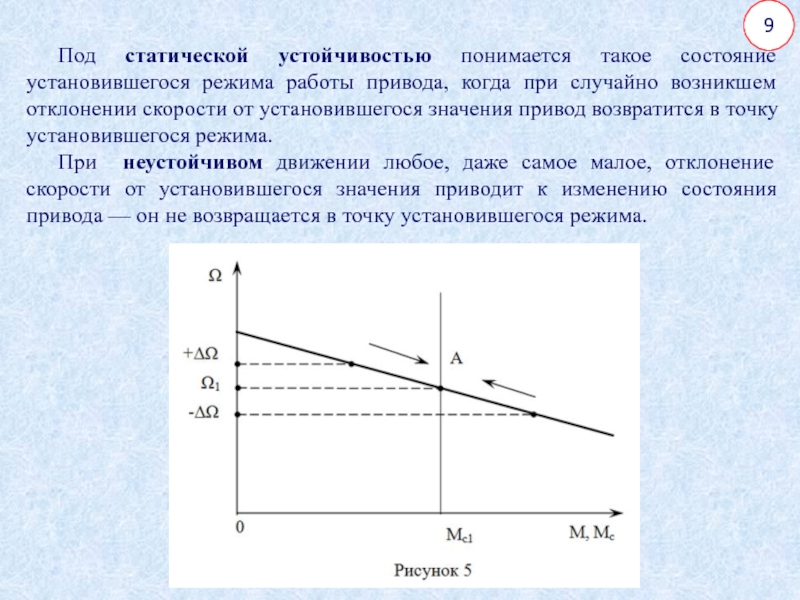
Под статической устойчивостью понимается такое состояние установившегося режима работы привода,
когда при случайно возникшем отклонении скорости от установившегося значения привод
возвратится в точку установившегося режима.При неустойчивом движении любое, даже самое малое, отклонение скорости от установившегося значения приводит к изменению состояния привода — он не возвращается в точку установившегося режима.
Слайд 1110
ЭД при моменте сопротивления Мс = Мс1 = const
работает в установившемся режиме со скоростью Ω1 в
точке А. Режим точки А характеризуется М = Мс1 .Выведем систему из равновесия.
1. Дадим (+) ΔΩ тогда Мс > М и М – Мс < 0 и ЭД тормозится до
Ω = Ω1, т.е. система возвращается в исходное состояние.
2.Дадим (–) ΔΩ, тогда М > Мс и М – Мс > 0 и ЭД разгоняется до
Ω = Ω1, т.е. система возвращается в исходное состояние.
Следовательно, работа ЭП – устойчива.
Если рассмотреть геометрические соотношения при анализе взаимного расположения характеристик, то условием статической устойчивости ЭП будет факт выполнения неравенства ,
так называемый, критерий статической устойчивости системы ЭП или
, или β – βс< 0.
Слайд 1211
Пример устойчивой и неустойчивой работы ЭП рассмотрим при работе АД
на нагрузку с Мс = сonst.
В точке N:
< 0, а βс = 0, тогда β – βс< 0, т.е. работа ЭПустойчива.
В точке М: > 0, а βс = 0 тогда β – βс> 0 т.е. работа ЭП
неустойчива.