Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принятие решений в условиях нечеткой информации
Содержание
- 1. Принятие решений в условиях нечеткой информации
- 2. Теория нечетких множествраздел прикладной математики, посвященный методам
- 3. Нечеткое управление одна из самых результативных областей применения теории нечетких множеств
- 4. Области использования приложений с нечеткой логикой в
- 5. Информация о системе носит субъективный характер
- 6. Fuzzy sets
- 7. Нечеткое множество Совокупность элементов, обладающих некоторым общим свойством, но … в разной степени
- 8. Нечеткое множество А в Хсовокупность пар вида
- 9. Слайд 9
- 10. ОпределенияsupμА(x) называется высотой нечеткого множества A
- 11. Носителем нечеткого множества А (supp A) с
- 12. Ядром нечеткого множестваназывается четкое подмножество универсального множества
- 13. α-сечением (или множеством α-уровня) нечеткого множестваназывается четкое
- 14. Слайд 14
- 15. Операции над нечеткими множестваминечеткие множества А и
- 16. Слайд 16
- 17. Пример 1. suppA = { x|
- 18. Примеры записи нечеткого множестваПусть Х = {x1,
- 19. A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5
- 20. Лингвистические переменные (linguistic variable) Терм–множеством (term
- 21. Лингвистическая переменная Х = "температура в комнате"универсальное множество U=[5; 35] ; терм-множество T={"холодно", "комфортно", "жарко"}
- 22. Слайд 22
- 23. Пример нечеткого множестваПусть Х= {0,1,2,..,10}, M =[0,1].
- 24. Построение функций принадлежности нечетких множеств прямые и
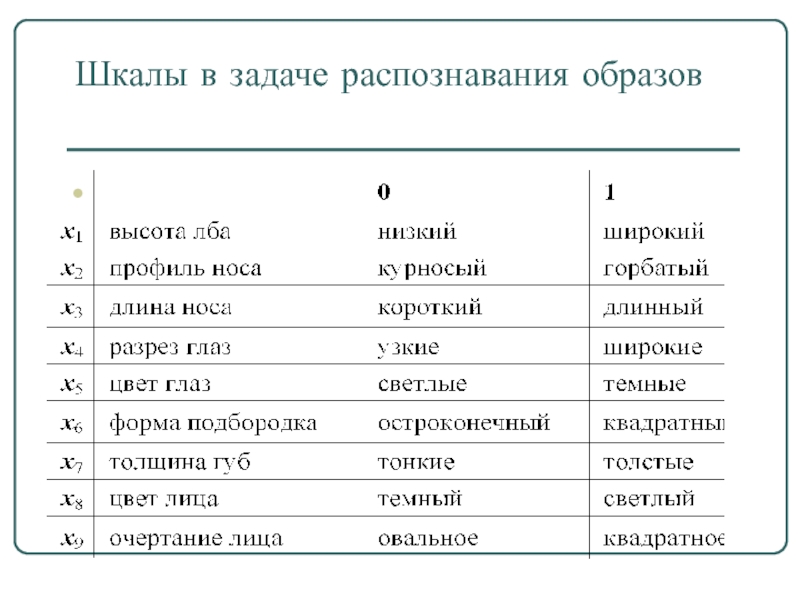
- 25. Шкалы в задаче распознавания образов
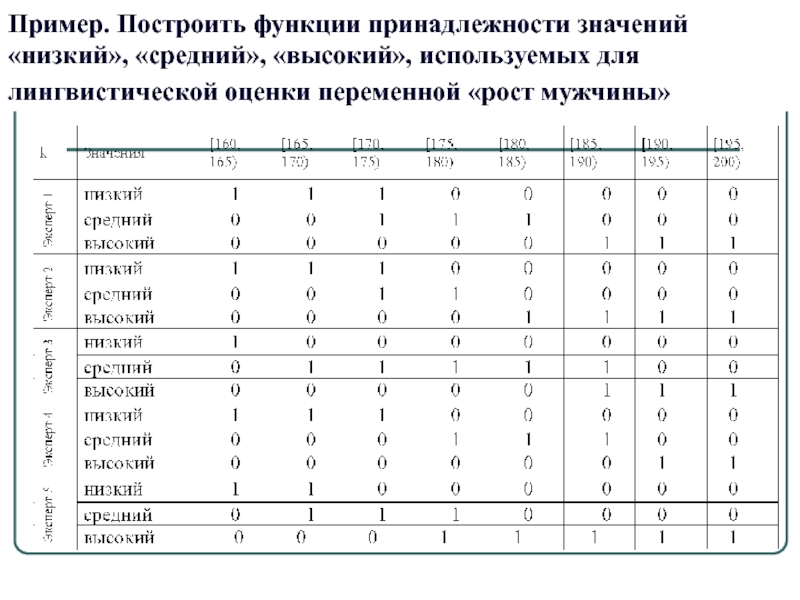
- 26. Пример. Построить функции принадлежности значений «низкий», «средний», «высокий», используемых для лингвистической оценки переменной «рост мужчины»
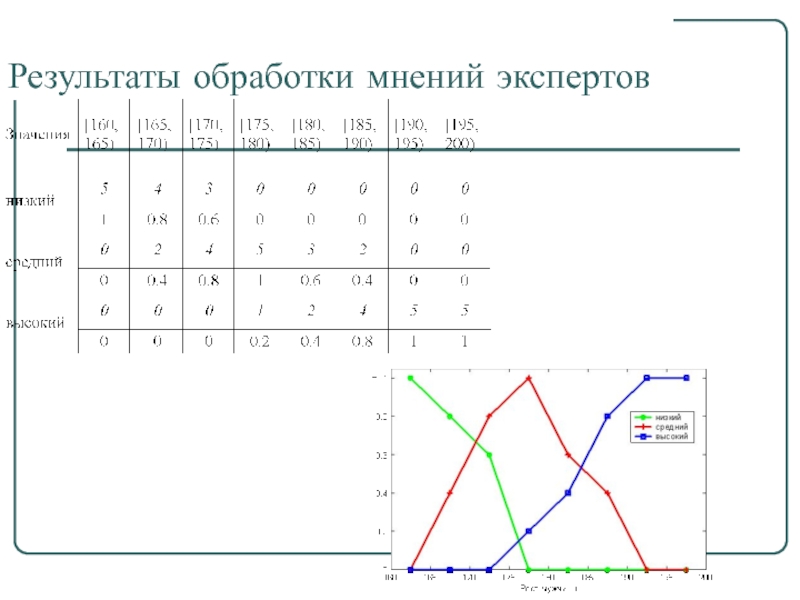
- 27. Результаты обработки мнений экспертов
- 28. Преобразования нечеткого множества Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число
- 29. Для многоэкстремальных функций принадлежности в Fuzzy Logic
- 30. Процедура дефаззификации аналогична нахождению характеристик
- 31. Метод центра тяжестиДефаззификация нечеткого множества по методу центра тяжести осуществляется по формуле
- 32. Физическим аналогом является нахождение центра
- 33. Для дискретного универсального множества дефаззификация нечеткого множества по методу центра тяжести осуществляется по формуле
- 34. Метод медианы Дефаззификация нечеткого множества по
- 35. Геометрическая интерпретация метода медианынахождение такой точки на
- 36. Для дискретного универсального множествадефаззификация нечеткого множества по методу медианы осуществляется по формуле
- 37. Метод центра максимумовДефаззификация нечеткого множества по методу
- 38. В методе центра максимумов находится среднее арифметическое
- 39. В методе центра максимумов находится среднее арифметическое
- 40. В дискретном случае дефаззификация по методам наибольшего
- 41. ПримерПровести дефаззификацию нечеткого множества «мужчина среднего роста»,
- 42. Решение:Применяя формулу
- 43. Задача достижения нечетко определенной цели (подход Беллмана-Заде)Пусть
- 44. Нечеткая цель GФункция принадлежности нечеткой цели
- 45. Пусть некоторая альтернатива x обеспечивает достижение цели
- 46. При наличии нескольких целей и ограниченийнечеткое решение описывается функцией принадлежности μD(x)=min{μG1(x),…,μGn(x),μC1(x),…,μCn(x)}
- 47. Оптимальной в смысле подхода Беллмана-Заде будет альтернатива
- 48.
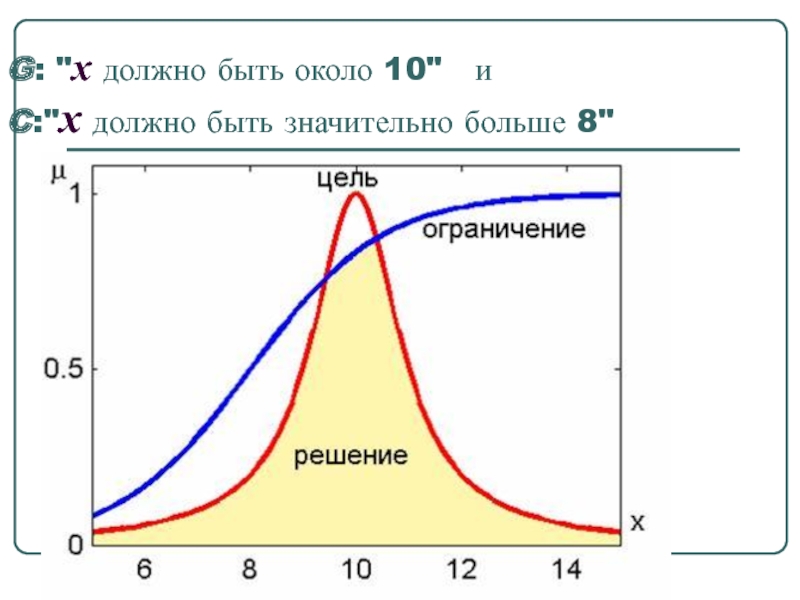
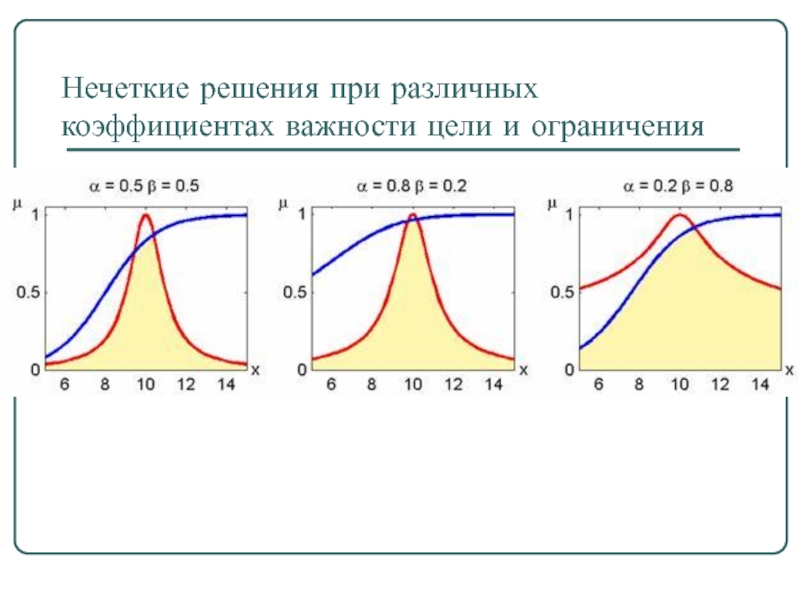
- 49. G: "x должно быть около 10" и C:"x должно быть значительно больше 8"
- 50. При принятии решения по схеме Беллмана-Заде не
- 51. Нечеткие решения при различных коэффициентах важности цели и ограничения
- 52. Скачать презентанцию
Теория нечетких множествраздел прикладной математики, посвященный методам анализа неопределенных данных, в которых описание неопределенностей реальных явлений и процессов проводится с помощью понятия о множествах, не имеющих четких границ
Слайды и текст этой презентации
Слайд 2Теория нечетких множеств
раздел прикладной математики, посвященный методам анализа неопределенных данных,
Слайд 3Нечеткое управление
одна из самых результативных областей применения теории
нечетких множеств
Слайд 4Области использования приложений с нечеткой логикой в Internet:
диагностика и восстановление
сетевых конфигураций и управление производственными объектами;
удаленный мониторинг устройств и
организация распределенных вычислений; всевозможные портативные гиды, доски объявлений с динамически изменяющимися свойствами и гибкой функциональностью;
интеллектуальные поисковые машины, распределенные системы загрузки и выделения данных
Слайд 5Информация о системе
носит субъективный характер и ее представление
в естественном языке содержит большое число неопределенностей типа
"много",
"мало",
"сильно увеличить",
"высокий",
"очень эффективный" и т.п.
Слайд 6Fuzzy sets
Л. Заде
Нечеткое множество - это математическая модель
класса с нечеткими, или размытыми границами 
Слайд 7Нечеткое множество
Совокупность элементов, обладающих некоторым общим свойством, но …
в разной степени
Слайд 8Нечеткое множество А в Х
совокупность пар вида
(x, μA(x)),
где x∈X,
μА : x→ [0,1] –
функция принадлежности (membership function)
нечеткого множества А
Значение μA(x) называется степенью принадлежности x нечеткому множеству А
Слайд 10Определения
supμА(x) называется высотой нечеткого множества A
Нечеткое множество A
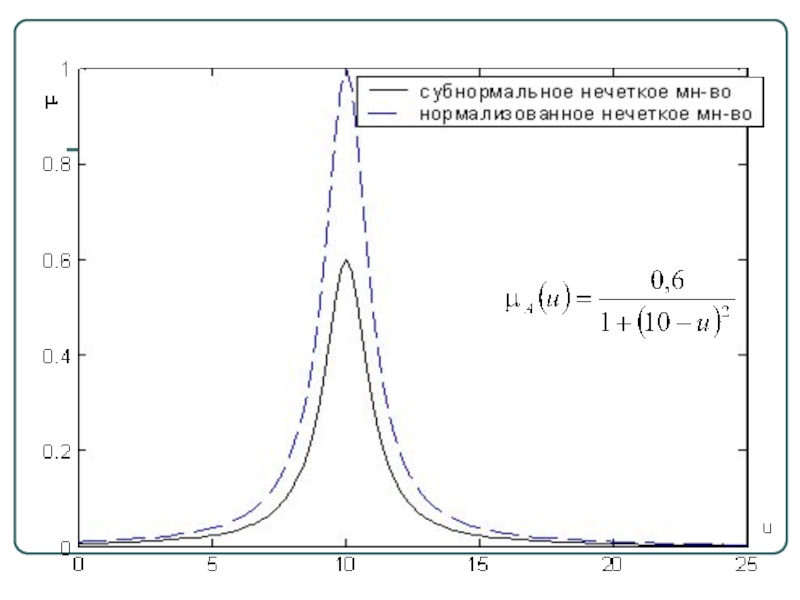
нормально, если его высота равна 1, т.е. верхняя граница его
функции принадлежности равна 1При sup μА(x)<1 нечеткое множество называется субнормальным
Слайд 11Носителем нечеткого множества А (supp A) с функцией принадлежности μA(x)
называется
множество вида
suppA={x|x∈X, μA(x)>0}
Для практических приложений носители нечетких множеств
всегда ограничены 
Слайд 12Ядром нечеткого множества
называется четкое подмножество универсального множества U, элементы которого
имеют степени принадлежности, равные единице
Ядро субнормального нечеткого множества пусто
Слайд 13α-сечением (или множеством α-уровня) нечеткого множества
называется четкое подмножество универсального множества
U, элементы которого имеют степени принадлежности, большие или равные α:
Слайд 15Операции над нечеткими множествами
нечеткие множества А и В равны, если
μA(x)=μВ(x);
нечеткое множество С является подмножеством В, т.е. С⊂ В,
если μС(x)≤ μВ(x); нечеткие множества можно объединять А∪ В, тогда μA∪В(x)= max {μA(x), μВ(x)};
нечеткие множества могут пересекаться А ∩ В, тогда μA∩В(x)= min {μA(x), μВ(x)};
5) прямое произведение нечетких множеств АхВ: μАxB(x)= μА(x)⋅ μB(x);
6) алгебраическая сумма A+B: μА+В(x)=μА(x)+μВ(x)-μАВ(x);
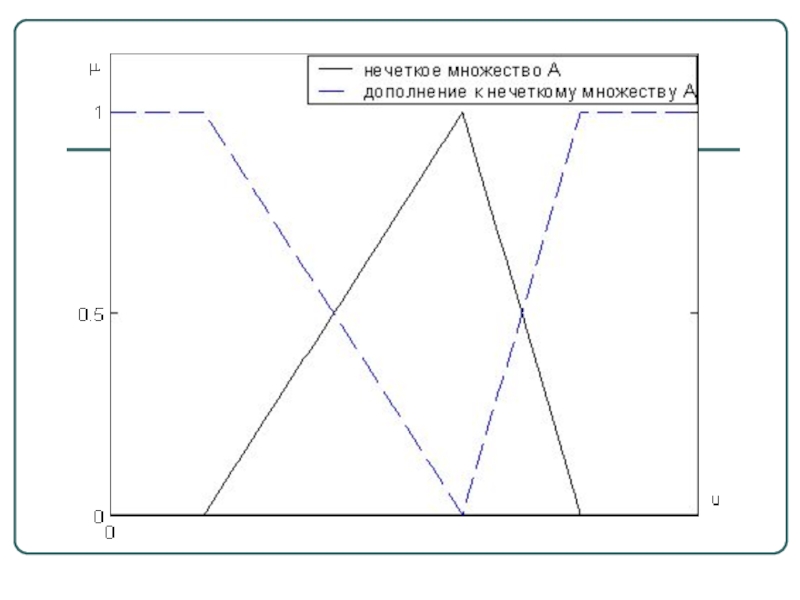
7) дополнением нечеткого множества А называется нечеткое множество с функцией принадлежности
Слайд 17Пример 1. suppA = { x| величина x близка к
1},
suppB = {x| величина x очень близка к 1}
Ясно, что
В⊆А, т.е. μA и μВ должны удовлетворять неравенству
μВ(x)≤μА(x) при любом x∈X.
А
В
Слайд 18Примеры записи нечеткого множества
Пусть Х = {x1, x2, x3, x4,
x5 },
M = [0,1];
A - нечеткое множество, для
которого μA(x1)=0,3;μA(x2)=0;μA(x3)=1;
μA(x4)=0,5; μA(x5)=0,9.
![Примеры записи нечеткого множестваПусть Х = {x1, x2, x3, x4, x5 }, M = [0,1]; A -](/img/thumbs/abef496836197e93d5724fc93c835179-800x.jpg "Принятие решений в условиях нечеткой информации Примеры записи нечеткого множестваПусть Х = {x1, x2, x3, x4, x5")
Слайд 19A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 },
или
A =
0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5,
или
х1
х2 х3 х4 х50,3 0 1 0,5 0,9
Слайд 20Лингвистические переменные
(linguistic variable)
Терм–множеством (term set) называется множество всех
возможных значений лингвистической переменной.
Термом (term) называется любой элемент терм–множества. В
теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.Например, лингвистическая переменная ВОЗРАСТ принимает нечеткие значения «юный», «молодой», «средний», «пожилой», «старый», и т.д., которые являются термами, образующими терм-множество.
Слайд 21Лингвистическая переменная
Х = "температура в комнате"
универсальное множество
U=[5; 35] ;
терм-множество
T={"холодно", "комфортно", "жарко"}
Слайд 23Пример нечеткого множества
Пусть Х= {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько"
можно определить следующим образом:
"несколько"={0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8} его характеристики:
высота = 1,
носитель={3,4,5,6,7,8}, точки перехода - {3,8}.
![Пример нечеткого множестваПусть Х= {0,1,2,..,10}, M =[0,1]. Нечеткое множество](/img/thumbs/722debab66fa327d7b8cb07ab9a291c5-800x.jpg "Принятие решений в условиях нечеткой информации Пример нечеткого множестваПусть Х= {0,1,2,..,10}, M =[0,1]. Нечеткое множество")
Слайд 24Построение функций принадлежности нечетких множеств
прямые и косвенные методы
прямые методы используются для измеримых понятий, таких как
скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения 
Слайд 26Пример. Построить функции принадлежности значений «низкий», «средний», «высокий», используемых для
лингвистической оценки переменной «рост мужчины»
Слайд 28Преобразования нечеткого множества
Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества
в четкое число
Слайд 29Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы методы
дефаззификации:
Centroid - центр тяжести;
Bisector - медиана;
LOM (Largest Of Maximums) - наибольший из
максимумов;SOM (Smallest Of Maximums) - наименьший из максимумов;
Mom (Mean Of Maximums) - центр максимумов.
Слайд 30Процедура дефаззификации
аналогична нахождению характеристик положения
(математического ожидания,
моды, медианы) случайных величин в теории вероятности
Простейшим
способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности 
Слайд 31Метод центра тяжести
Дефаззификация нечеткого множества
по методу центра тяжести
осуществляется
по формуле
Слайд 32 Физическим аналогом является нахождение центра тяжести плоской фигуры,
ограниченной осями координат и графиком функции принадлежности нечеткого множества
Слайд 33Для дискретного универсального множества
дефаззификация нечеткого множества
по методу центра
тяжести осуществляется по формуле
Слайд 34Метод медианы
Дефаззификация нечеткого множества
по методу медианы состоит
в нахождении такого числа a, что
Слайд 35Геометрическая интерпретация метода медианы
нахождение такой точки на оси абцисс, что
перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции
принадлежности на две равные части
Слайд 36Для дискретного универсального множества
дефаззификация нечеткого множества по методу медианы осуществляется
по формуле
Слайд 37Метод центра максимумов
Дефаззификация нечеткого множества
по методу центра максимумов осуществляется
по формуле
где G – множество всех элементов из интервала [u1;u2], имеющих
максимальную степень принадлежности нечеткому множеству .
Слайд 38
В методе центра максимумов находится среднее арифметическое элементов универсального множества,
имеющих максимальные степени принадлежностей. Если множество таких элементов конечно, то
где |G| – мощность множества G.
Слайд 39В методе центра максимумов находится среднее арифметическое элементов универсального множества,
имеющих максимальные степени принадлежности.
Если множество таких элементов конечно, то
где |G| – мощность множества G.
Слайд 40В дискретном случае дефаззификация по методам наибольшего из максимумов и
наименьшего из максимумов осуществляется по формулам
a=max(G) и
a=min(G)
соответственно.
Слайд 41Пример
Провести дефаззификацию нечеткого множества «мужчина среднего роста»,
для которого нечеткое
множество =
{0/155; 0.1/160; 0.3/165; 0.8/170; 1/175; 1/180; 0.5/185; 0/190}, по
методу центра тяжести
Слайд 42Решение:
Применяя формулу
,
получаем:
{0/155; 0.1/160;
0.3/165; 0.8/170; 1/175; 1/180; 0.5/185; 0/190}
Слайд 43Задача достижения нечетко определенной цели (подход Беллмана-Заде)
Пусть Х – универсальное
множество альтернатив,
т.е. универсальная совокупность всевозможных выборов ЛПР
Нечеткой целью
является нечеткое подмножество X, которое мы будем обозначать G,
Слайд 44Нечеткая цель G
Функция принадлежности нечеткой цели
μG: X →
[0,1].Чем больше степень принадлежности альтернативы x нечеткому множеству цели μG,
т.е. чем больше значение μG(x),
тем больше степень достижения этой цели при выборе альтернативы x в качестве решения.
Слайд 45Пусть некоторая альтернатива x обеспечивает достижение цели со степенью μG(x),
удовлетворяет ограничениям со степенью μС(x)
Решить задачу – означает достичь цели
и удовлетворить ограничениям. Таким образом, нечетким решением задачи достижения нечеткой цели называется пересечение нечетких множеств цели и ограничений,
т.е. функция принадлежности решений μD имеет вид:
μD(x) = min {μG (x), μC (x)}.
Слайд 46При наличии нескольких целей и ограничений
нечеткое решение описывается функцией принадлежности
μD(x)=min{μG1(x),…,μGn(x),μC1(x),…,μCn(x)}
Слайд 47Оптимальной в смысле подхода
Беллмана-Заде будет альтернатива х*,
для которой
μD(x) максимальна
х*:
μD(x*)=max μD(x)x∈X
Слайд 48 - коэффициент
относительной
важности i-ой цели, - коэффициент относительной важности j-го ограничения
Слайд 50При принятии решения по схеме Беллмана-Заде не делается никакого различия
между целью и ограничениями.
Всякое разделение на цель и ограничения
является условным: можно поменять местами цель с ограничением, при этом решение не изменится 
