Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ: Аксиомы стереометрии. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В
Содержание
- 1. РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ: Аксиомы стереометрии. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В
- 2. Задание 1 Вставьте пропущенные слова Единственную
- 3. Задание 2 Определите: верно, ли утверждение? НетНетДаДаНет
- 4. Задание 2 Определите: верно, ли утверждение? НетНетНетДа
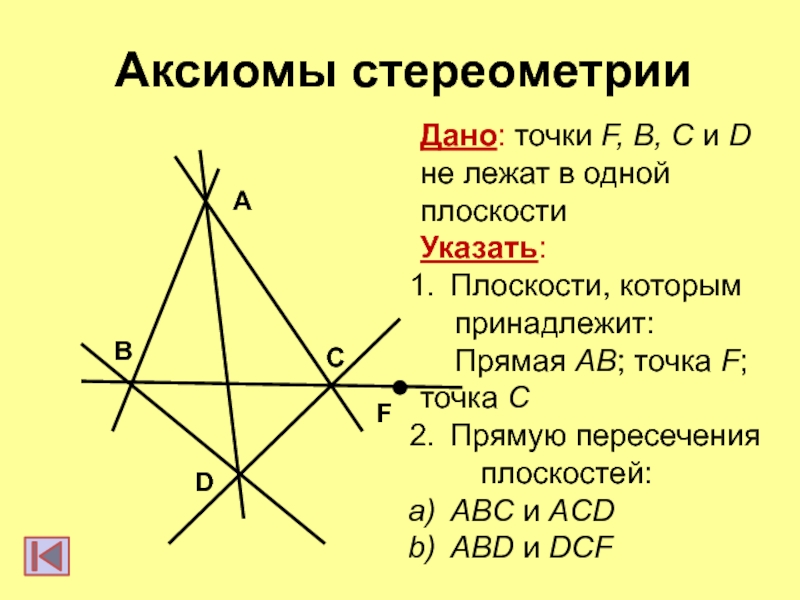
- 5. Аксиомы стереометрииCDBFAДано: точки F, B, C и
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
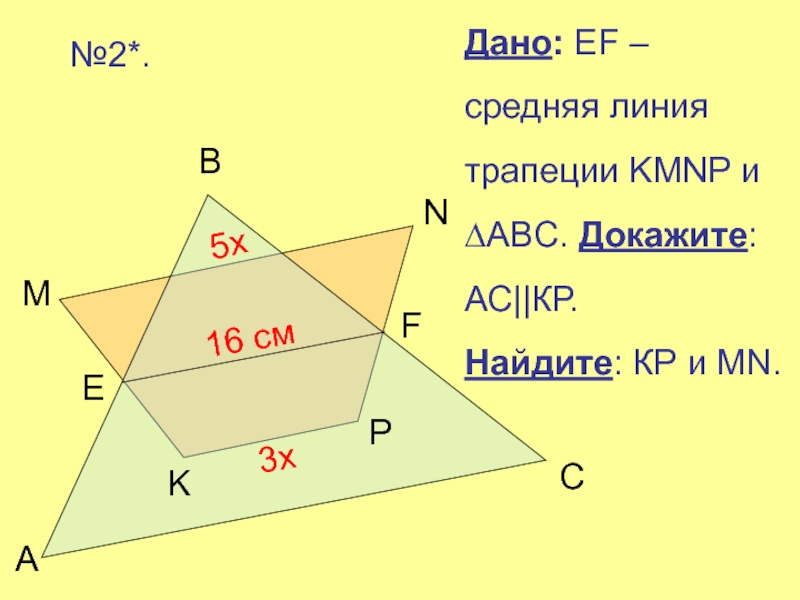
- 9. Дано: EF – средняя линия трапеции KMNP
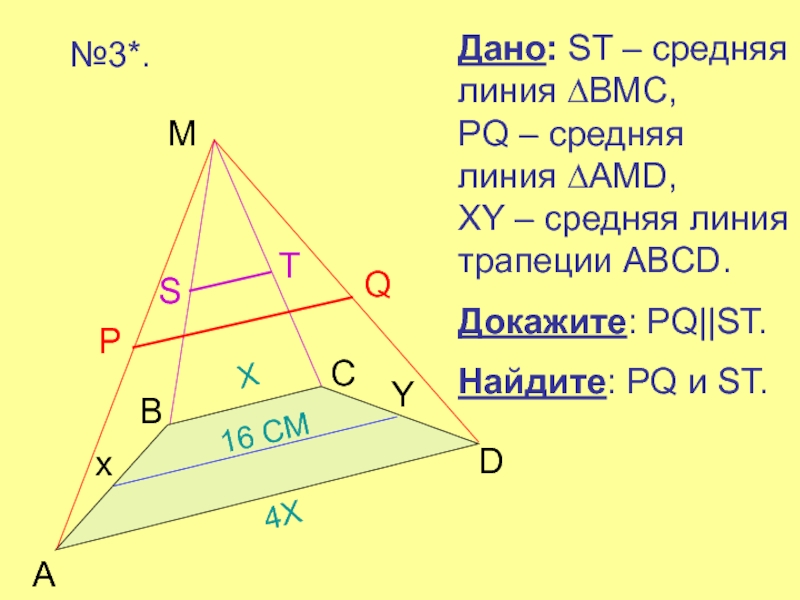
- 10. Дано: ST – средняя линия ∆BMC,
- 11. На данном рисунке плоскость содержит
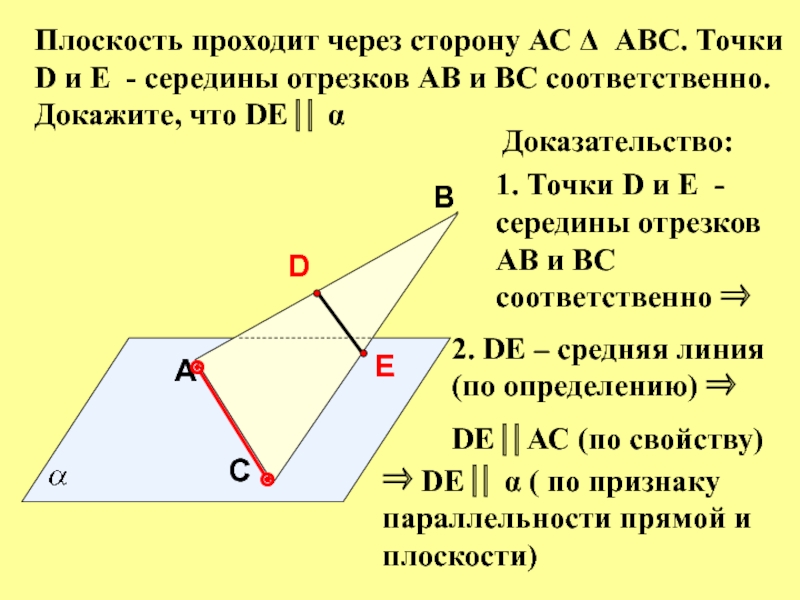
- 12. AВСПлоскость проходит через сторону АС АВС.
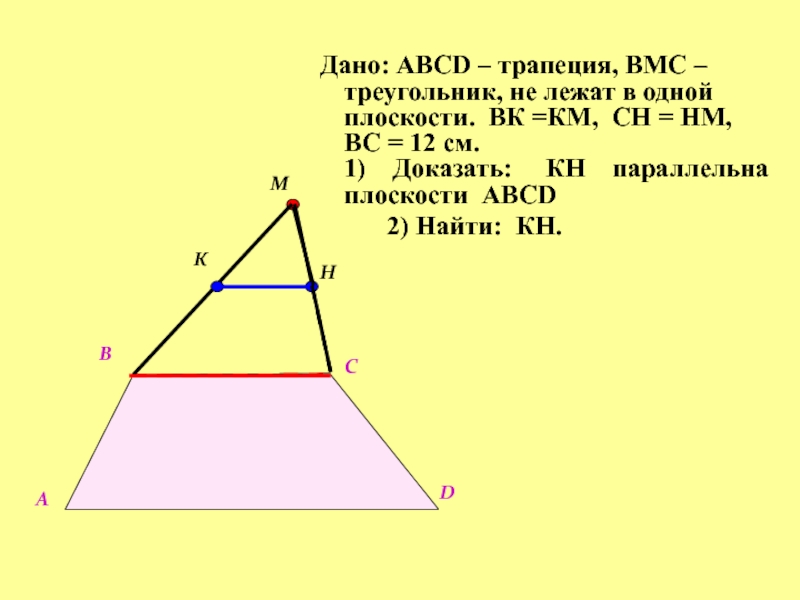
- 13. Дано: АВСD – трапеция, ВМС – треугольник,
- 14. Решение задач.№3.Прямая МК параллельна стороне СД ромба
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Задание 1 Вставьте пропущенные слова
Единственную плоскость можно задать
через три точки, при этом они
на одной прямой.2) Если точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
3) Две различные плоскости могут иметь только одну общую
4) Прямые являются в пространстве, если они не пересекаются и в одной плоскости.
5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке
В
α, то прямые а и b
не лежат
две
прямую
параллельными
лежат
скрещивающиеся
Слайд 5Аксиомы стереометрии
C
D
B
F
A
Дано: точки F, B, C и D
не лежат
в одной
плоскости
Указать:
Плоскости, которым
принадлежит:
Прямая AB; точка
F; точка С
Прямую пересечения
плоскостей:
ABC и ACD
ABD и DCF
Слайд 10Дано: ST – средняя линия ∆BMC, PQ
– средняя линия ∆AMD, XY – средняя
линия трапеции ABCD.Докажите: PQ||ST.
Найдите: PQ и ST.
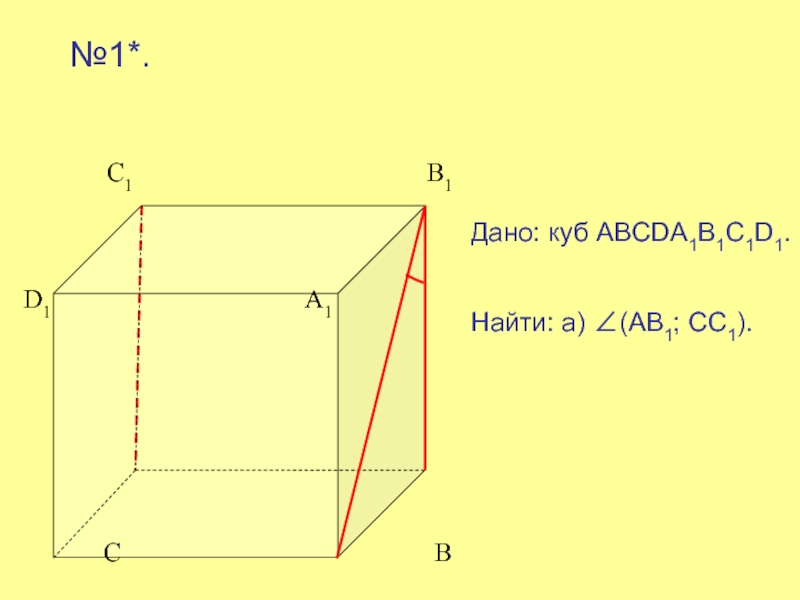
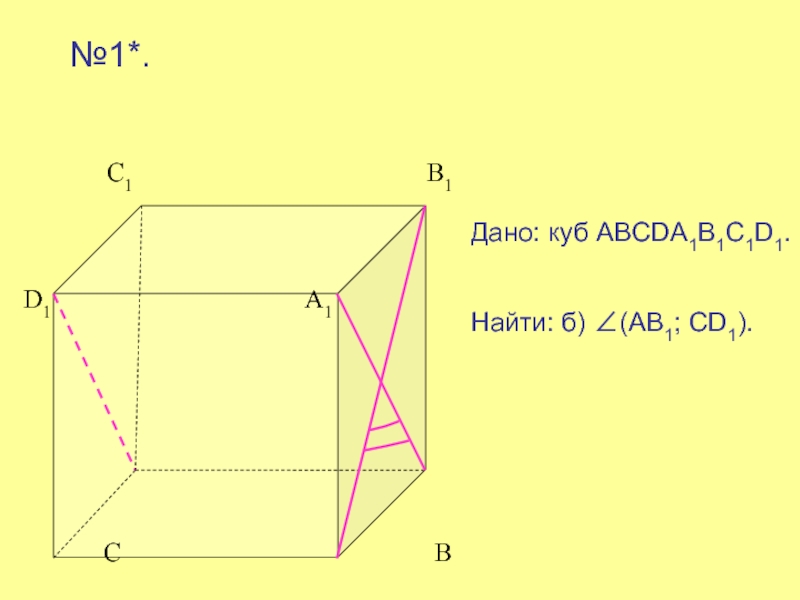
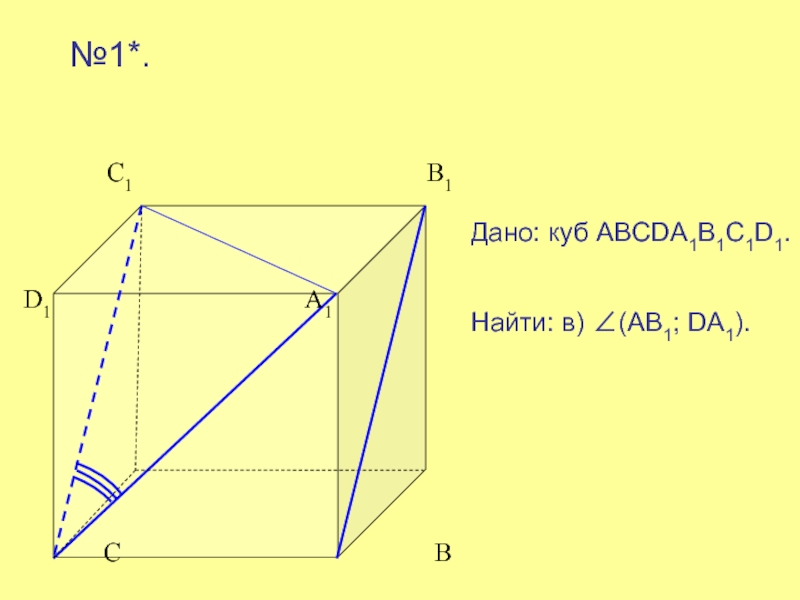
№3*.
Слайд 11На данном рисунке плоскость содержит точки А, В,
С, Д, но не содержит точку М. Постройте точку К
– точку пересечения прямой АВ и плоскости МСД. Лежит ли точка К в плоскости .А
В
С
Д
М
Задача 4
К
Решение:
Слайд 12A
В
С
Плоскость проходит через сторону АС АВС. Точки D и
E - середины отрезков АВ и BC соответственно. Докажите, что
DE αДоказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно
2. DE – средняя линия (по определению)
DE АС (по свойству)
DE α ( по признаку параллельности прямой и плоскости)
Слайд 13Дано: АВСD – трапеция, ВМС – треугольник, не лежат в
одной плоскости. ВК =КМ, СН = НМ, ВС =
12 см. 1) Доказать: КН параллельна плоскости АВСD2) Найти: КН.
А
В
С
D
М
К
Н
Слайд 14Решение задач.№3.
Прямая МК параллельна стороне СД ромба АВСД
и не
лежит в плоскости ромба.
а) Выясните взаимное
расположение прямых МК и ВС
б) Найдите угол между прямыми МК и ВС, если
M
K