Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
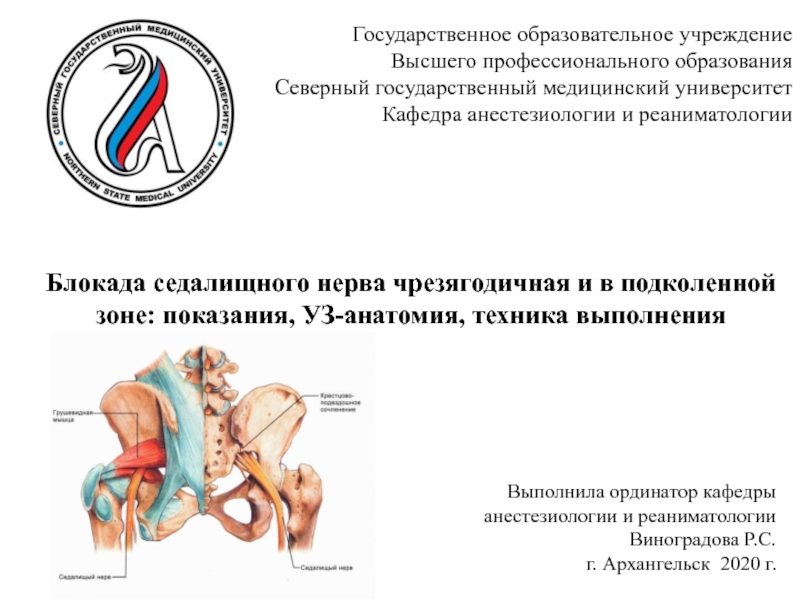
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение
Содержание
- 1. Движение
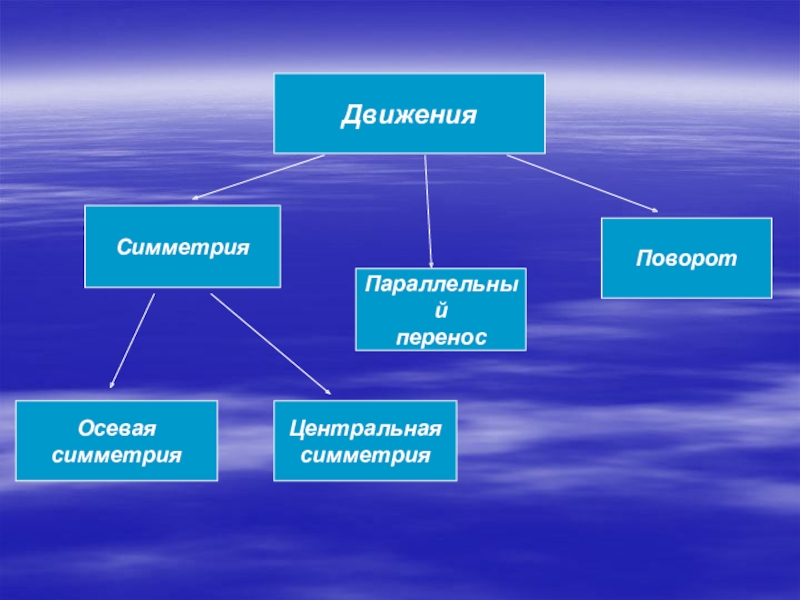
- 2. ДвиженияСимметрияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
- 3. Осевая симметрия Определение Осевая
- 4. ПостроениеПусть а – ось симметрии.
- 5. Слайд 5
- 6. Слайд 6
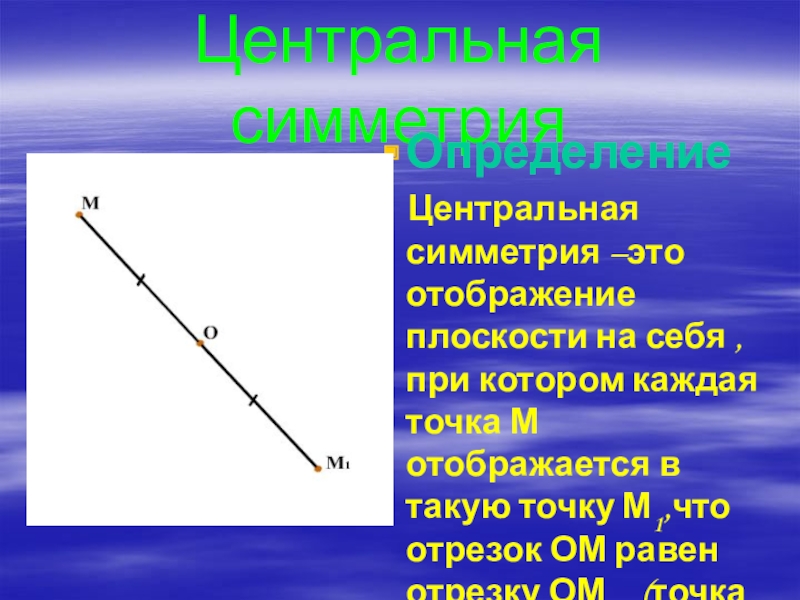
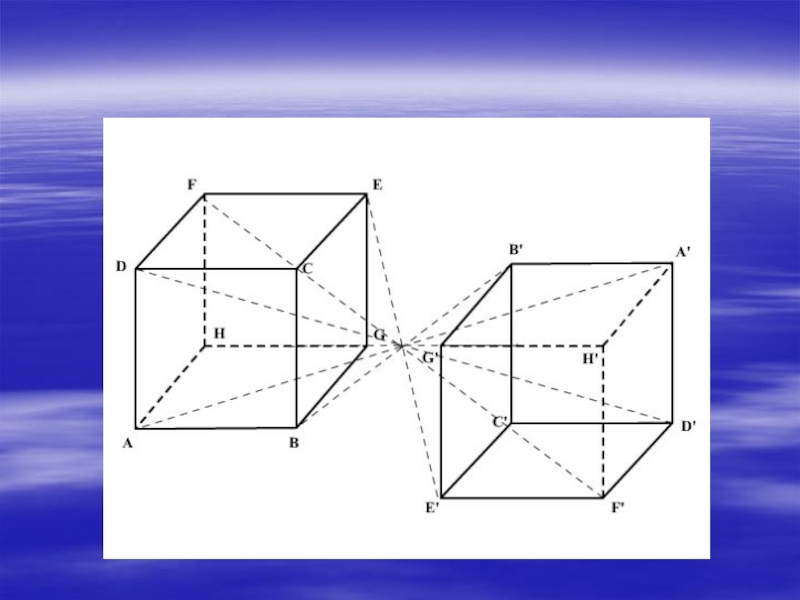
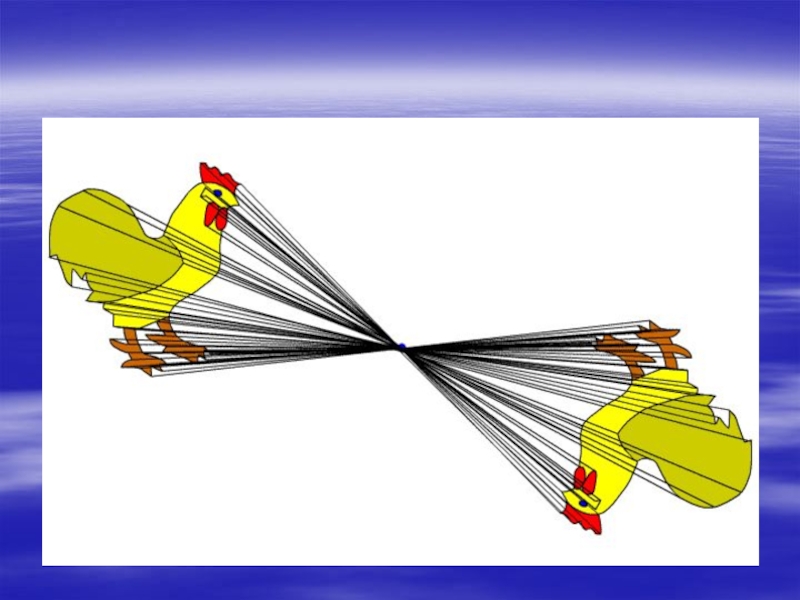
- 7. Центральная симметрияОпределение Центральная симметрия –это отображение
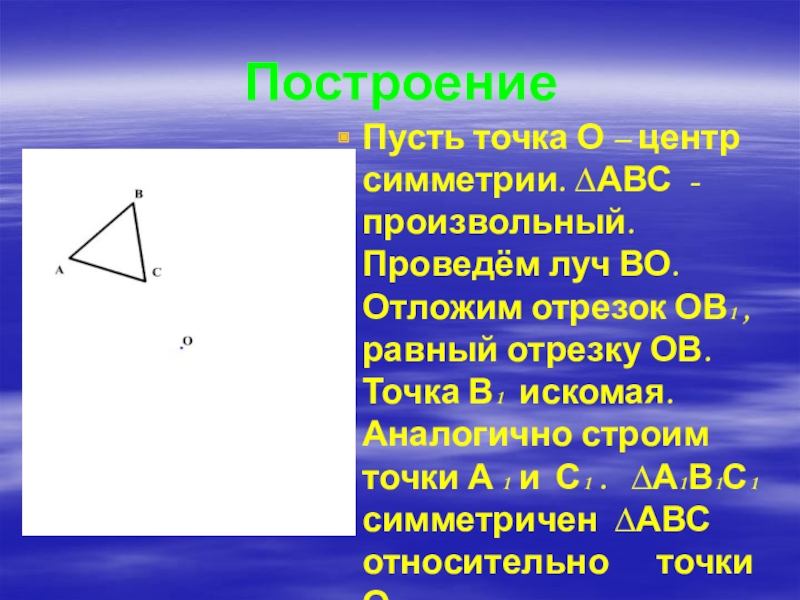
- 8. ПостроениеПусть точка О – центр симметрии. ∆АВС
- 9. Слайд 9
- 10. Слайд 10
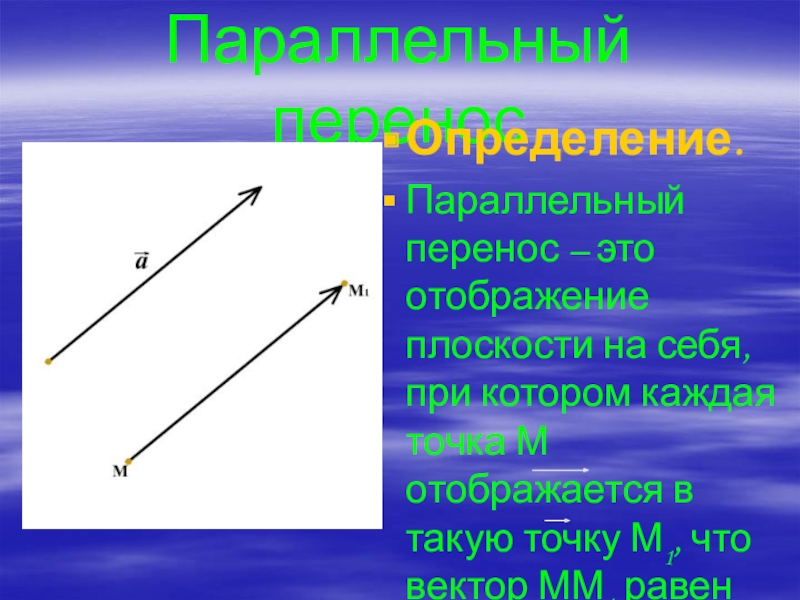
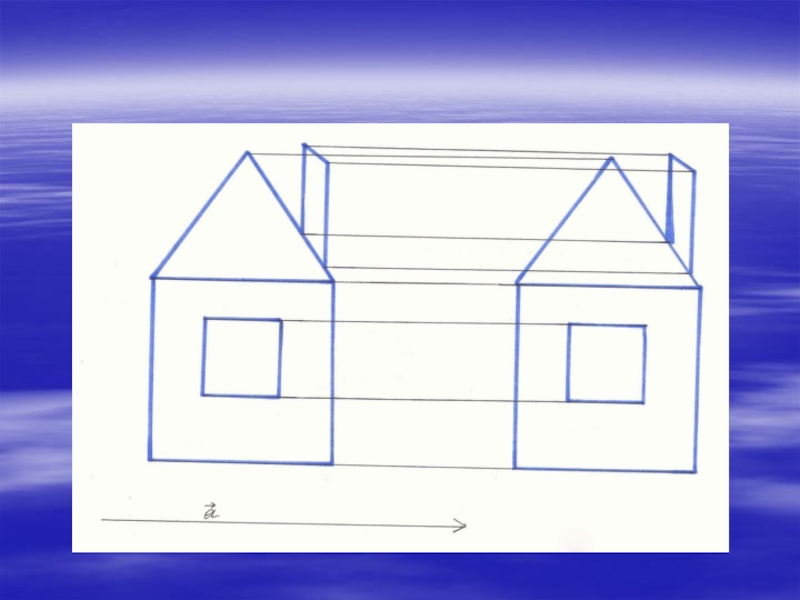
- 11. Параллельный переносОпределение. Параллельный перенос – это отображение
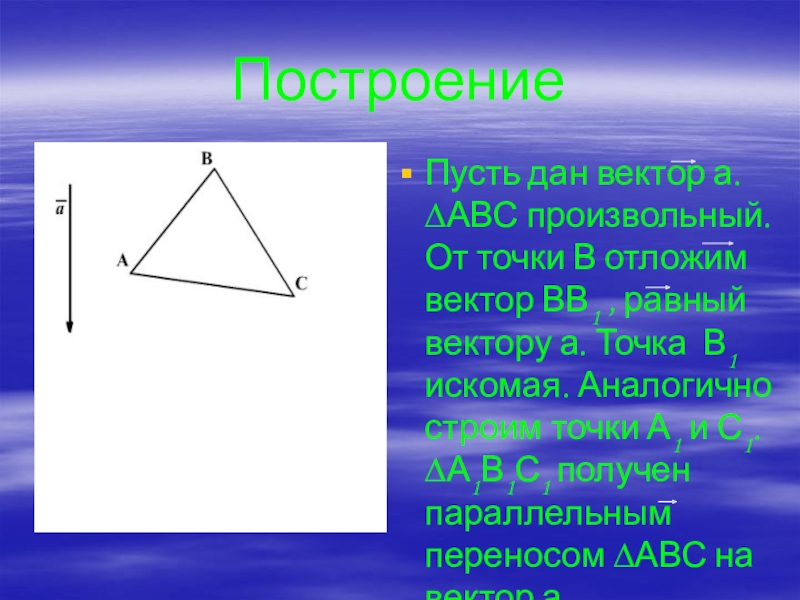
- 12. ПостроениеПусть дан вектор а. ∆АВС произвольный. От
- 13. Слайд 13
- 14. Слайд 14
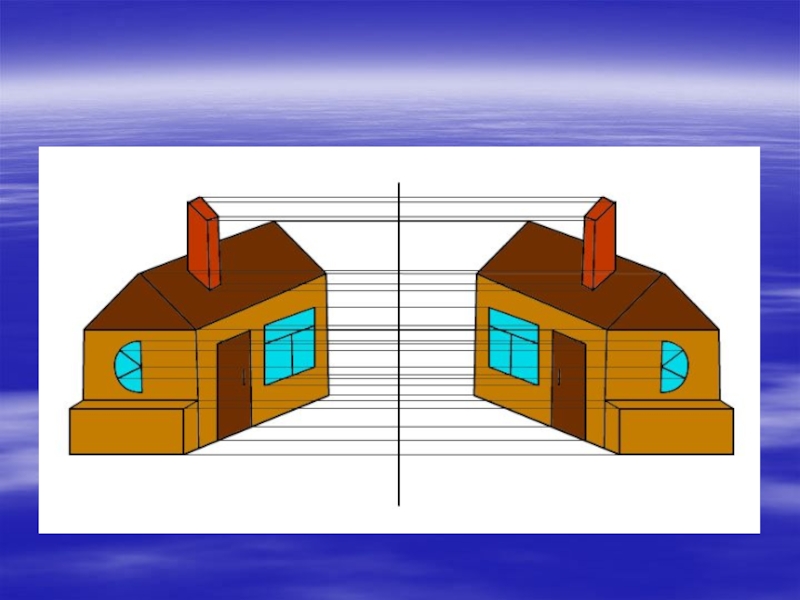
- 15. Движение в архитектуре. Определить вид движения.
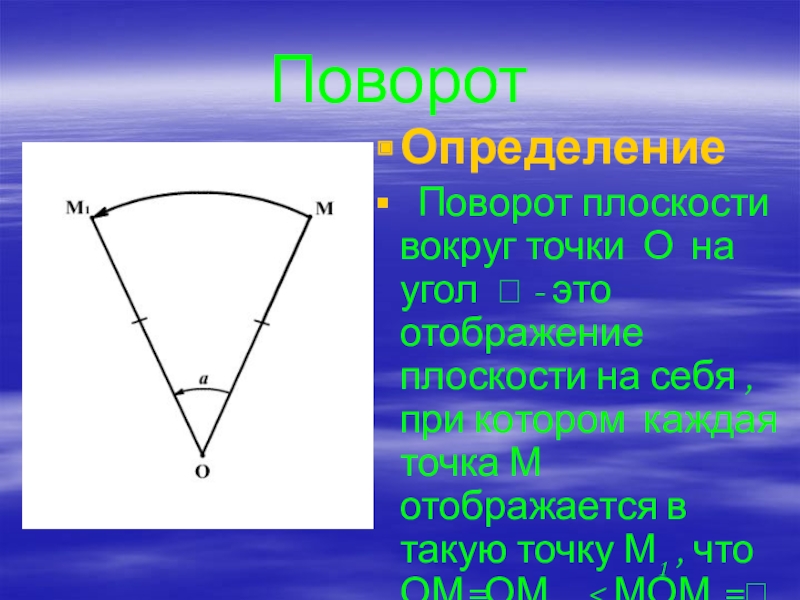
- 16. ПоворотОпределение Поворот плоскости вокруг точки
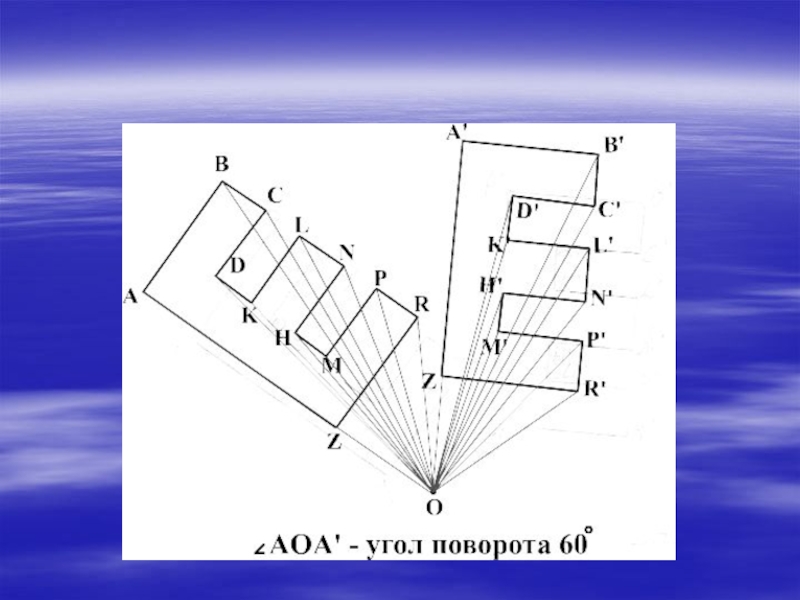
- 17. ПостроениеПусть О – центр поворота, =90º, ∆АВС
- 18. Слайд 18
- 19. Слайд 19
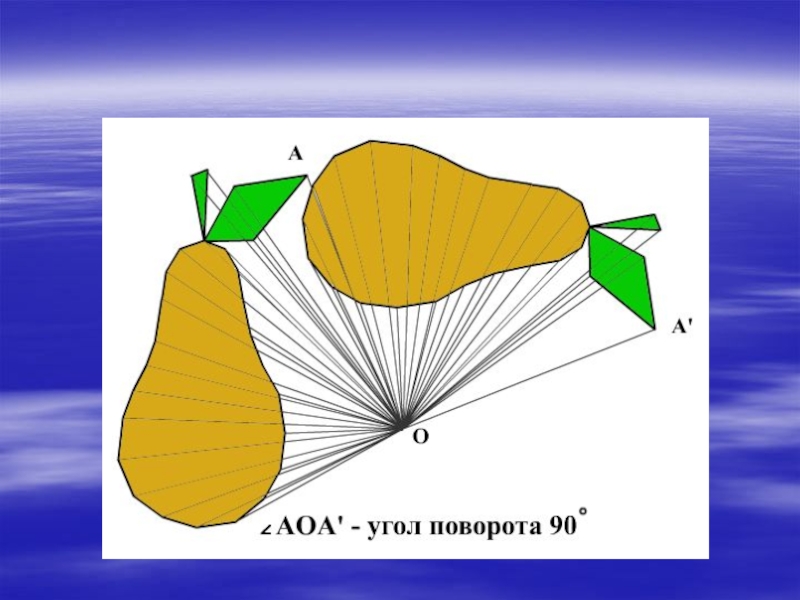
- 20. Симметрия в природе
- 21. Слайд 21
- 22. Слайд 22
- 23. Симметрия в архитектуре
- 24. Слайд 24
- 25. Скачать презентанцию
ДвиженияСимметрияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
Слайды и текст этой презентации
Слайд 4Построение
Пусть а – ось симметрии.
∆АВС – произвольный.
Проведем перпендикуляр ВР к прямой а. Отложим на прямой ВР
отрезок РВ1 , равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 7Центральная симметрия
Определение
Центральная симметрия –это отображение плоскости на себя
, при котором каждая точка М отображается в такую точку
М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
Слайд 8Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 , равный отрезку ОВ. Точка В1
искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
Слайд 11Параллельный перенос
Определение.
Параллельный перенос – это отображение плоскости на себя,
при котором каждая точка М отображается в такую точку М1,
что вектор ММ1 равен вектору а.
Слайд 12Построение
Пусть дан вектор а. ∆АВС произвольный. От точки В отложим
вектор ВВ1 , равный вектору а. Точка В1 искомая. Аналогично
строим точки А1 и С1. ∆А1В1С1 получен параллельным переносом ∆АВС на вектор а.
Слайд 16Поворот
Определение
Поворот плоскости вокруг точки О на угол
- это отображение плоскости на себя , при котором
каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 , < МОМ1=.
Слайд 17Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём
отрезок АВ, от него по часовой стрелке отложим
равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
