Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Примеры расчета потенциала по известным полям
Содержание
- 1. Примеры расчета потенциала по известным полям
- 2. 2.7.1. Разность потенциалов между двумя бесконечными заряженными плоскостями
- 3. Мы показали, что напряженность связана с потенциалом
- 4. Чтобы получить выражение для потенциала между
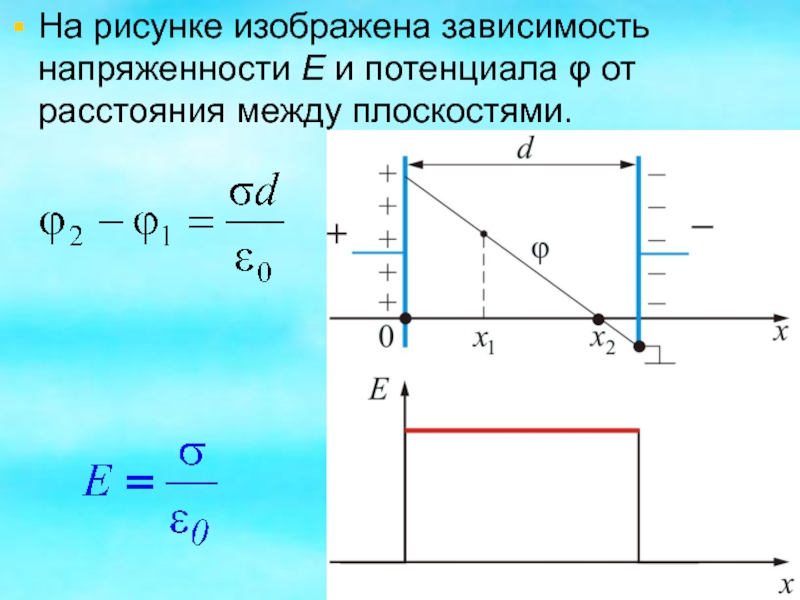
- 5. На рисунке изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями.
- 6. 2.7.2. Разность потенциалов между точками поля, образованного
- 7. Тогда,т.к. отсюда следует, что разность потенциалов
- 8. Слайд 8
- 9. 2.7.3. Разность потенциалов между обкладками
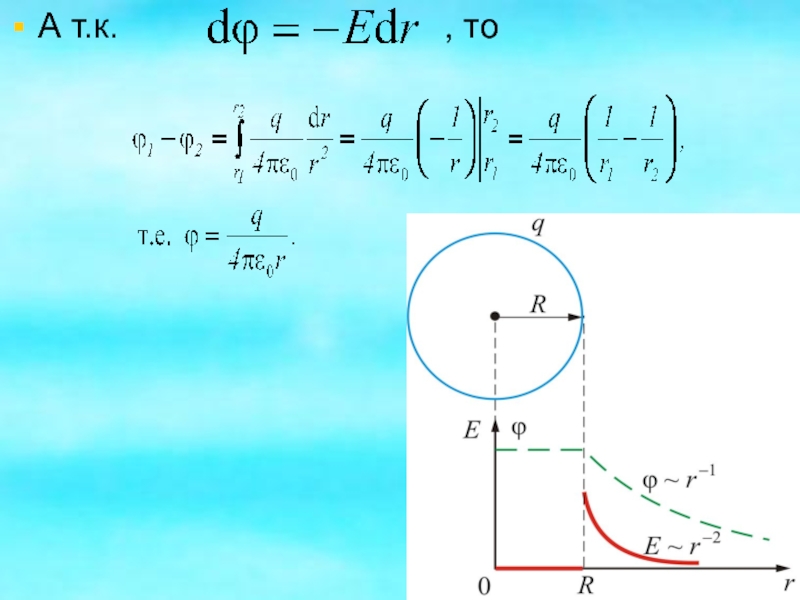
- 10. Т.к. , то
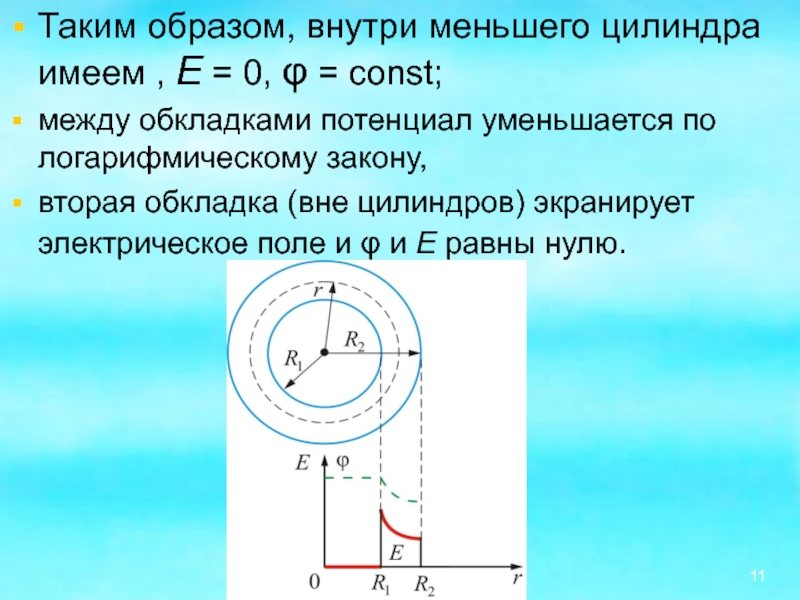
- 11. Таким образом, внутри меньшего цилиндра имеем ,
- 12. 2.7.4. Разность потенциалов заряженной сферы (пустотелой) Напряженность поля сферы определяется формулой
- 13. А т.к.
- 14. Слайд 14
- 15. 2.7.5. Разность потенциалов внутри диэлектрического заряженного шара Имеем диэлектрический шар заряженный с объемной плотностью
- 16. Напряженность поля шара, вычисленная с помощью теоремы
- 17. Отсюда найдем разность потенциалов шара:
- 18. Потенциал шара:
- 19. Из полученных соотношений можно сделать следующие выводы:С
- 20. Скачать презентанцию
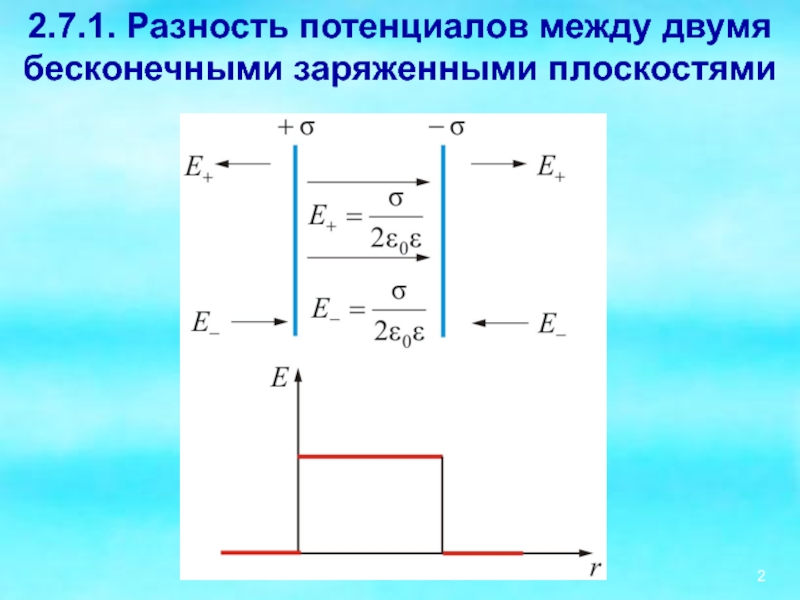
2.7.1. Разность потенциалов между двумя бесконечными заряженными плоскостями
Слайды и текст этой презентации
Слайд 12.7. ВЫЧИСЛЕНИЕ ПО ИЗВЕСТНОМУ ПОТЕНЦИАЛА
Рассмотрим несколько примеров вычисления разности потенциалов
между точками поля, созданного некоторыми заряженными телами
Слайд 3Мы показали, что напряженность связана с потенциалом
тогда
(2.17)
где – напряженность электростатического поля между заряженными плоскостями
σ = q/S – поверхностная плотность заряда.
Слайд 4 Чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение
При x1 = 0 и x2 = d (2.18)
Слайд 5На рисунке изображена зависимость напряженности E и потенциала φ от
расстояния между плоскостями.
Слайд 62.7.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической
поверхностью
С помощью теоремы Остроградского-Гаусса
мы показали, что
Слайд 11Таким образом, внутри меньшего цилиндра имеем , Е = 0,
φ = const;
между обкладками потенциал уменьшается по логарифмическому закону,
вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.
Слайд 122.7.4. Разность потенциалов заряженной сферы (пустотелой)
Напряженность поля сферы определяется формулой
Слайд 152.7.5. Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар заряженный
с объемной плотностью
Слайд 19Из полученных соотношений можно сделать следующие выводы:
С помощью теоремы Гаусса
сравнительно просто можно рассчитать Е и φ от различных заряженных
поверхностей.Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.