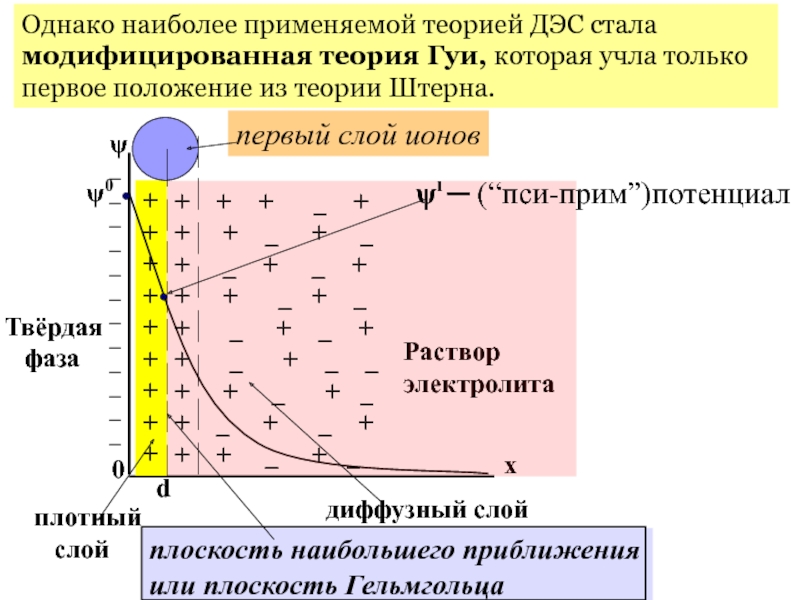
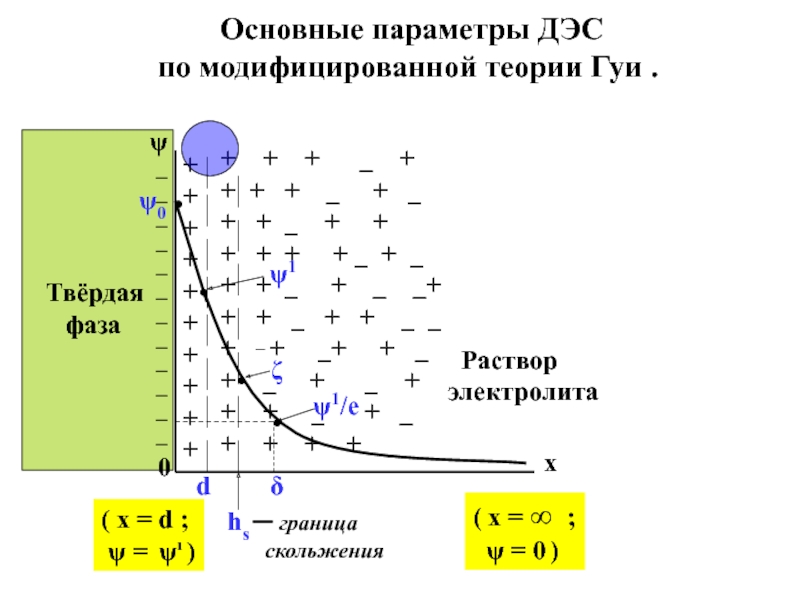
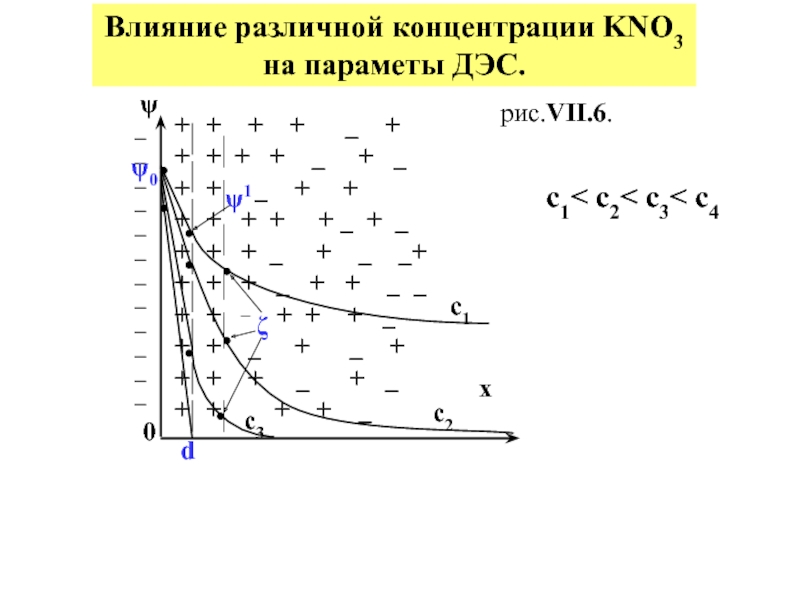
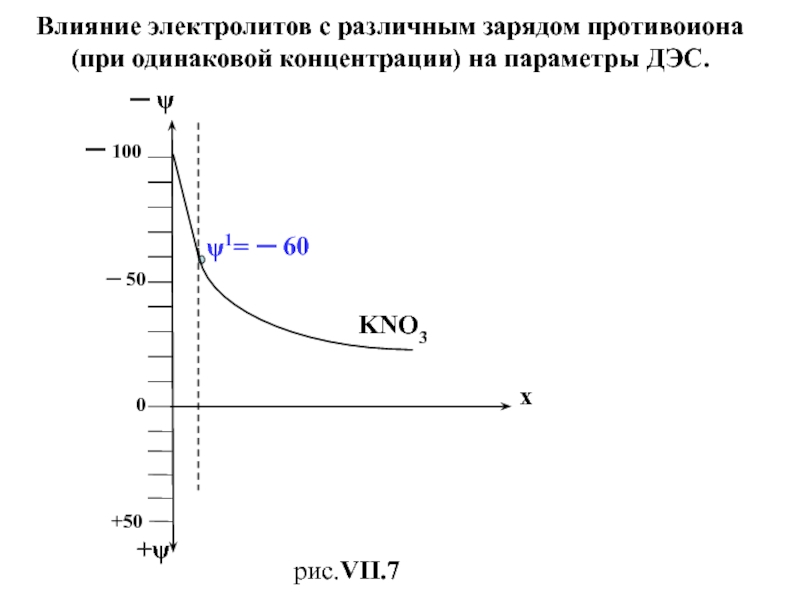
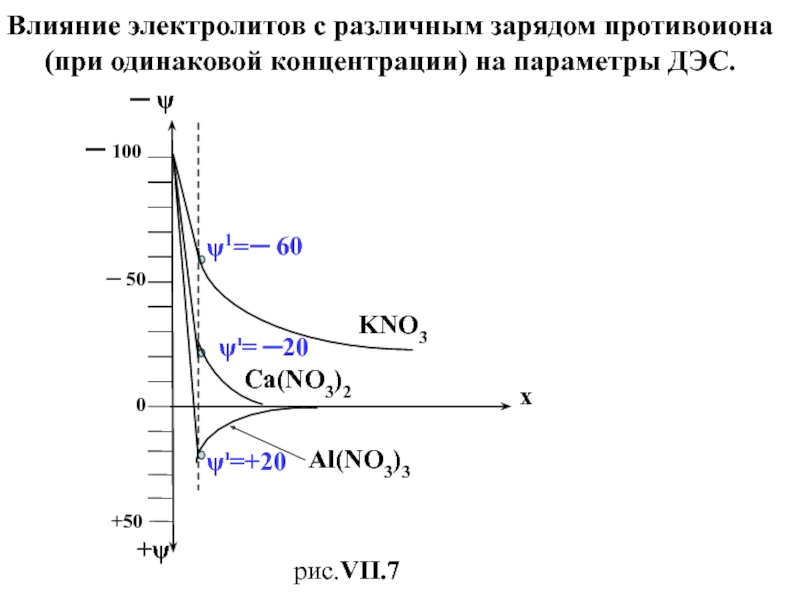
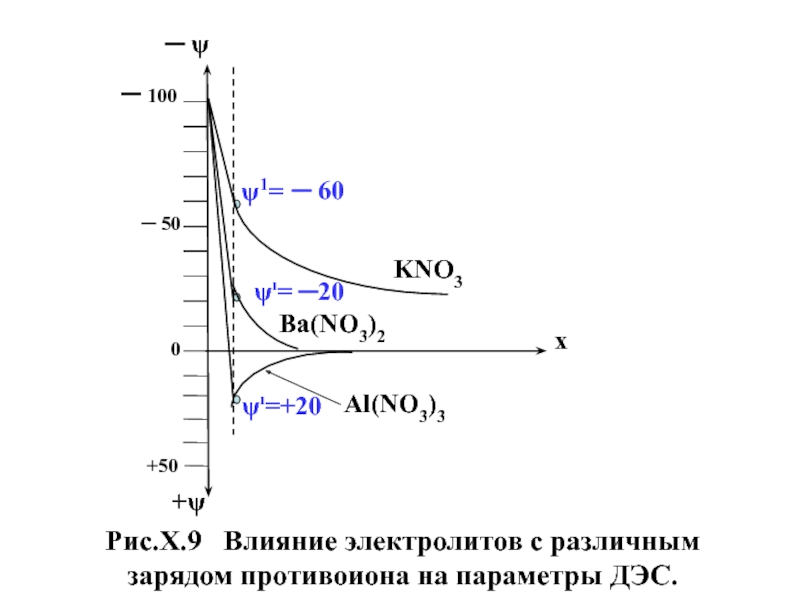
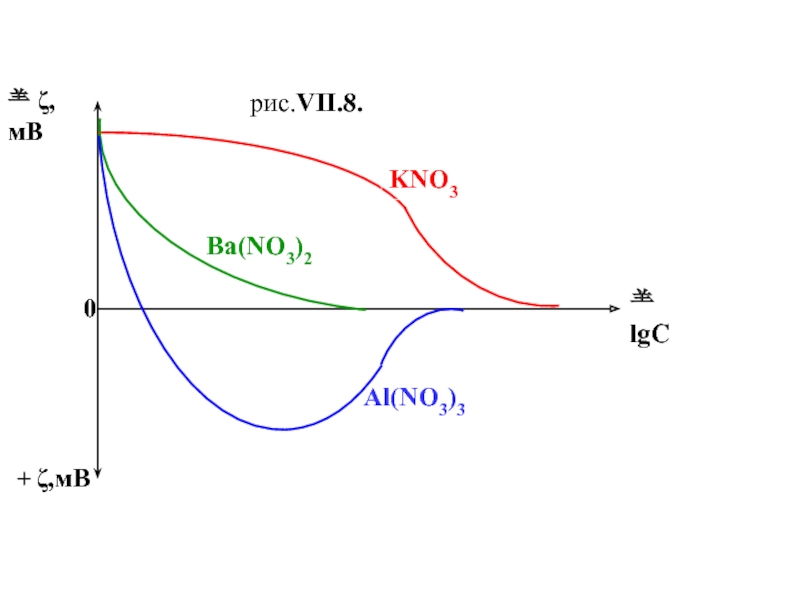
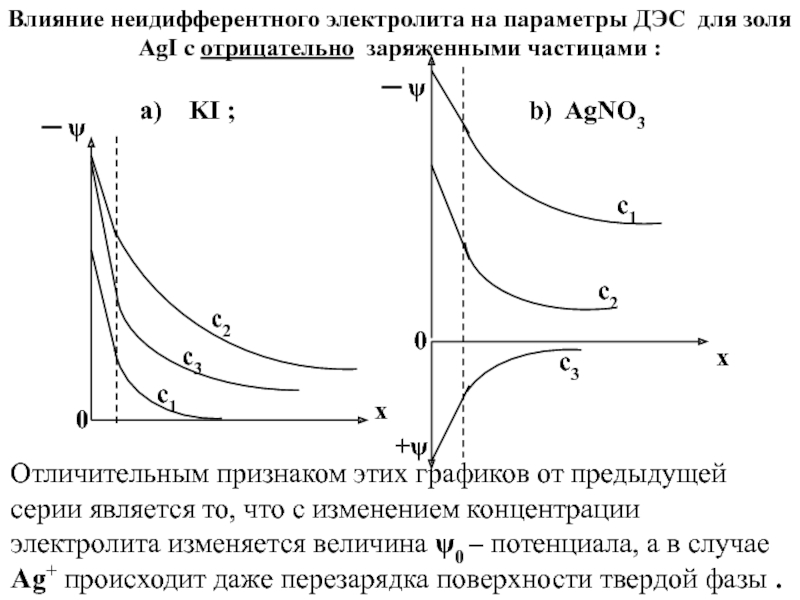
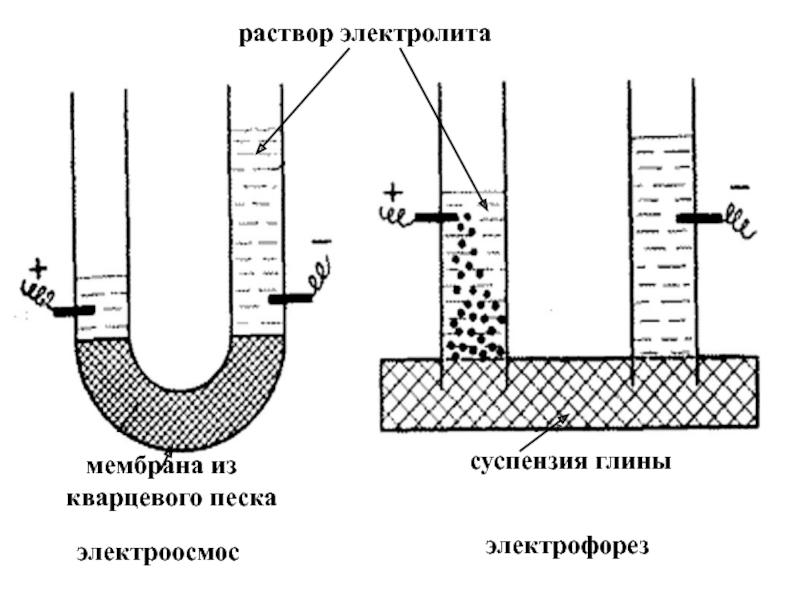
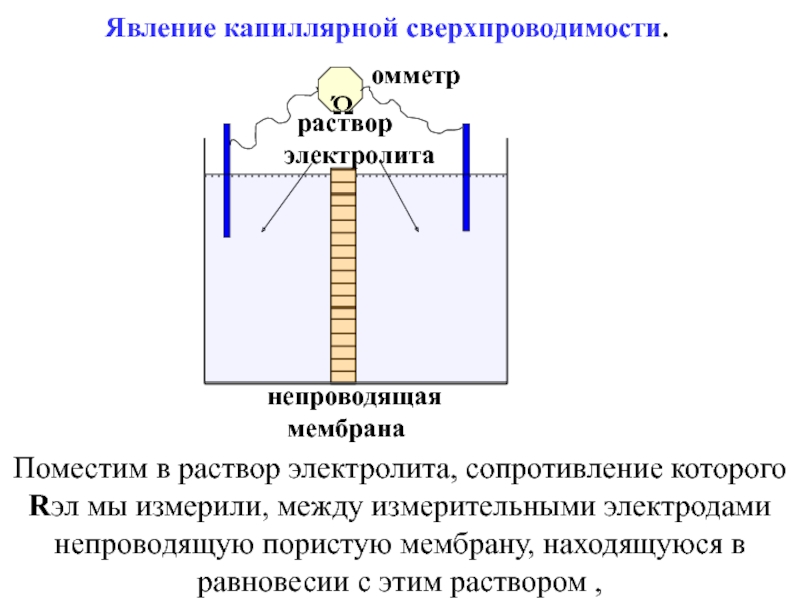
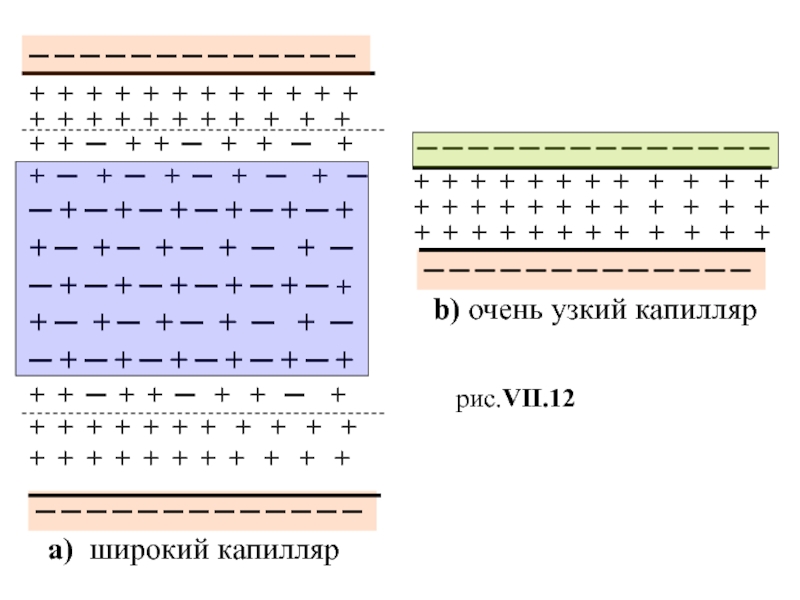
электролита
μiж ≠ μiт В случае переноса заряженных ионов электрохимический потенциал (VII.1) μi = μi + ziF ψ , где
zi — валентность i – го компонента ; F – число Фарадея ; ψ – электрический потенциал .
Условия равновесия при образовании ДЭС
μiт + ziF ψт = μiж + ziF ψж
Обозначив μiт — μiж = ∆μi , а ψт — ψж = ∆ψ, получим выражение для межфазного скачка потенциала :
(VII.2) ∆ψ = — ∆μi / ziF .


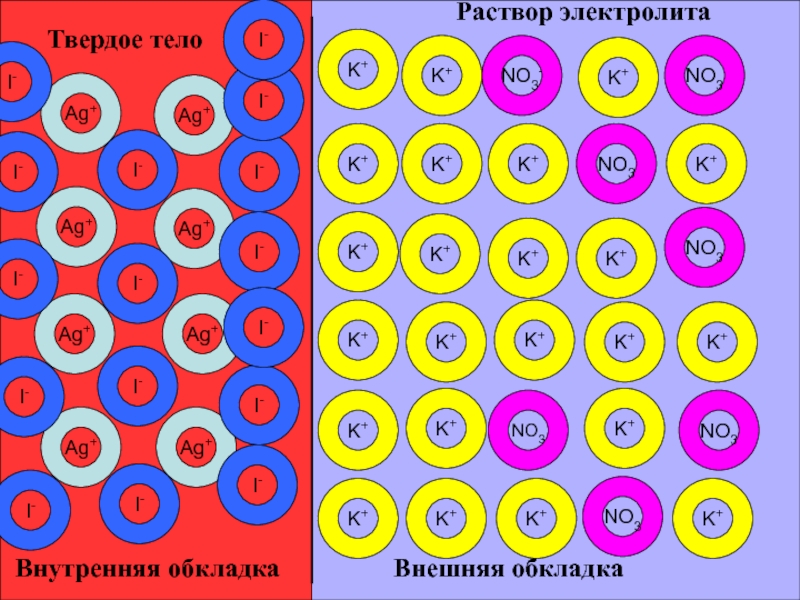



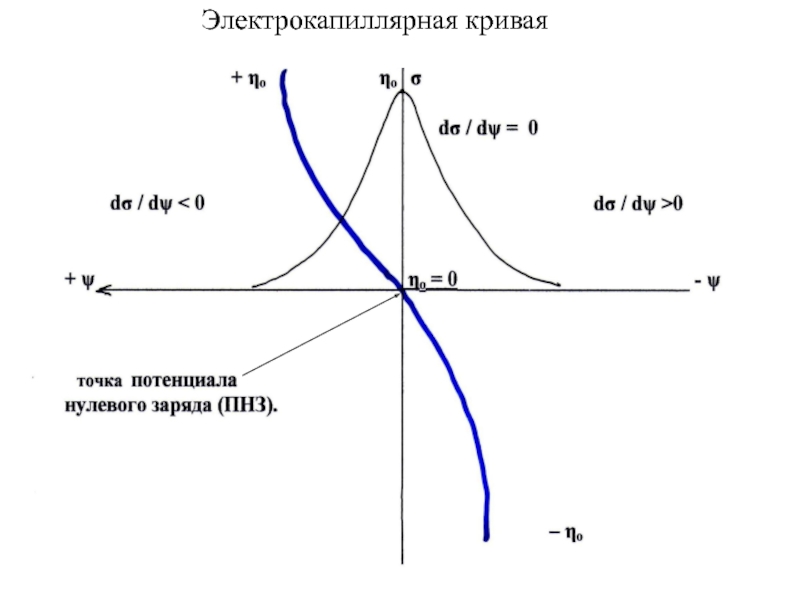
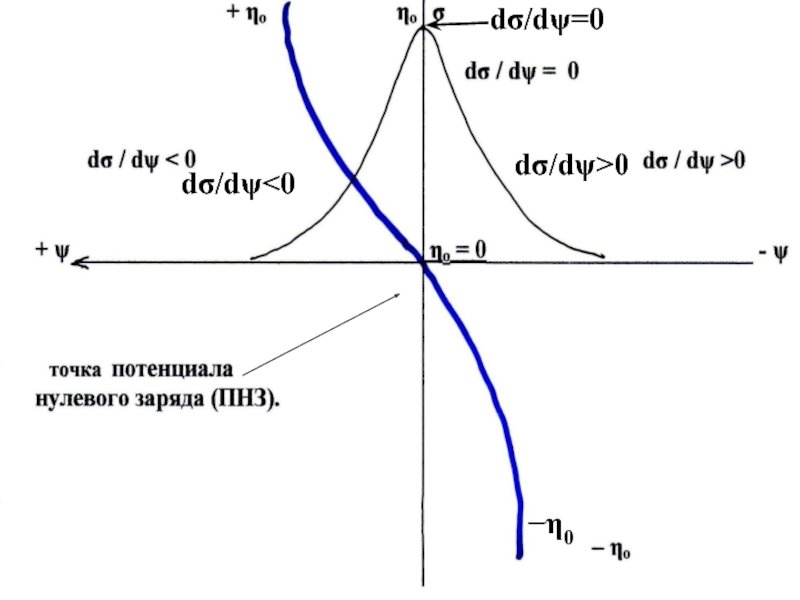

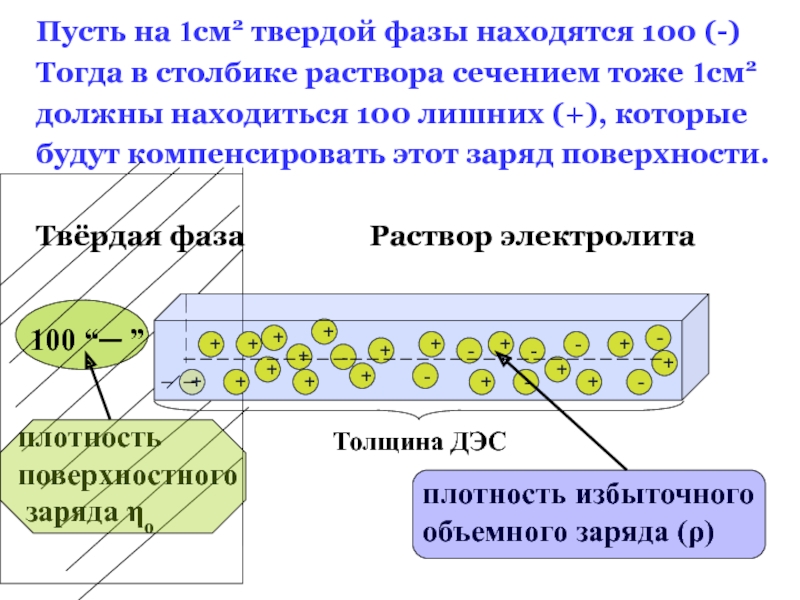



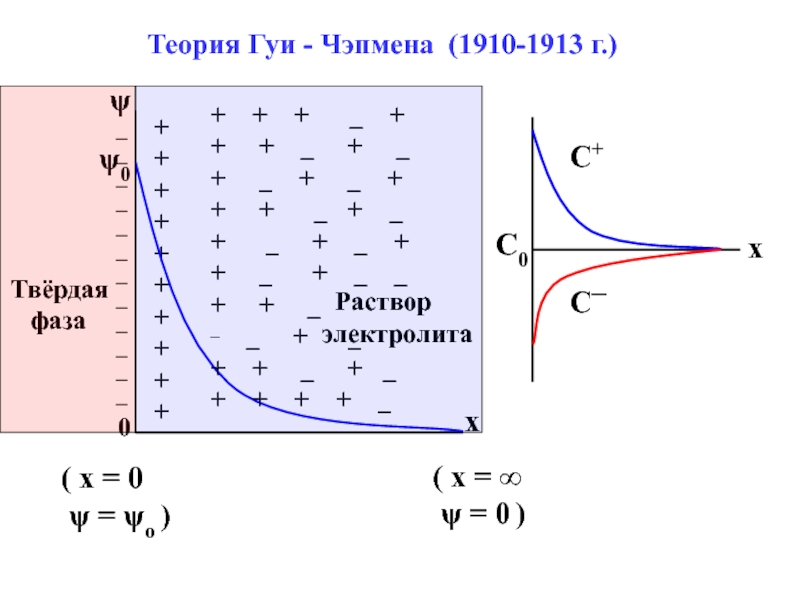
![Двойной электрический слой на границе раздела твердое тело / раствор электролита (VII.8) ηо= √ 2εε0RTCo *[exp( zFψо / 2RT) – exp(– zFψо (VII.8) ηо= √ 2εε0RTCo *[exp( zFψо / 2RT) – exp(– zFψо / 2RT)], [exp( zF ψо /](/img/thumbs/d752b4567ff13cbf11501f30a68d4f5a-800x.jpg)

![Двойной электрический слой на границе раздела твердое тело / раствор электролита ─ η0 =++ z+*FГ∞ z─ *FГ∞ 1+[exp (Ф++ z+*Fψ1) / 2RT]/18c+1+[exp ─ η0 =++ z+*FГ∞ z─ *FГ∞ 1+[exp (Ф++ z+*Fψ1) / 2RT]/18c+1+[exp (Ф─+ z─*Fψ1) / 2RT]/18c─+2εε0RTCo*[exp( zF ψ1](/img/thumbs/181686bb583fdb47bf64b41e23c5a75e-800x.jpg)