Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двойственный симплекс-метод Приведем к каноническому виду, введя дополнительные
Содержание
- 1. Двойственный симплекс-метод Приведем к каноническому виду, введя дополнительные
- 2. Умножим второе и третье структурное ограничение на (-1)
- 3. Векторы А3, А4, А5
- 4. Чаще всего псевдоплан появляется в задачах, в
- 5. Теорема. Признак оптимальности псевдоплана. Пусть х* =
- 6. Алгоритм двойственного симплекс-метода(1)Мы имеем систему ограничений вида:
- 7. Правило 1. Определение номера вектора, выводимого из
- 8. Правило 2. Определение номера вектора, вводимого в
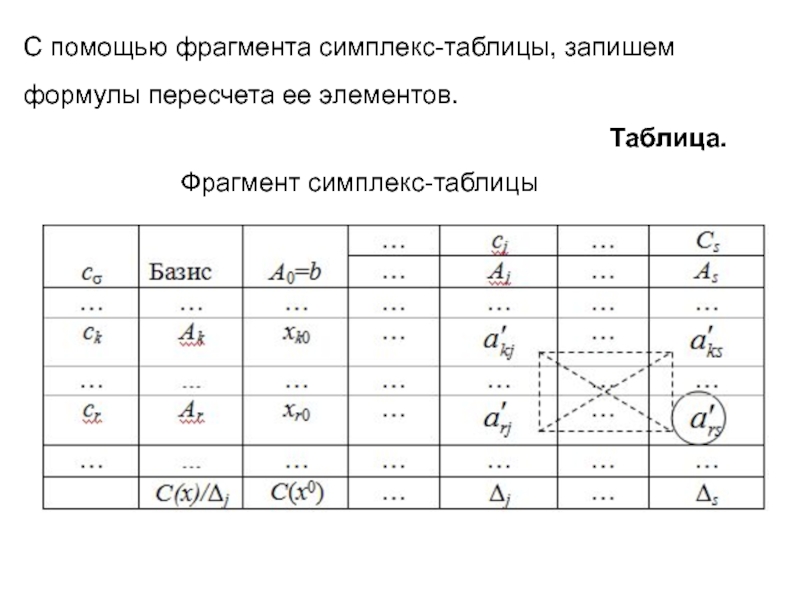
- 9. С помощью фрагмента симплекс-таблицы, запишем формулы пересчета ее элементов.Таблица. Фрагмент симплекс-таблицы
- 10. Компоненты нового псевдоплана определяются согласно (3).(3)Другие элементы симплексной таблицы вычисляются по формулам: (4)
- 11. Двойственные оценки:(5)Значение целевой функции на новом псевдоплане: (6)
- 12. Теорема 10.Применение правил 1 и 2, а
- 13. П р и м е р 15.
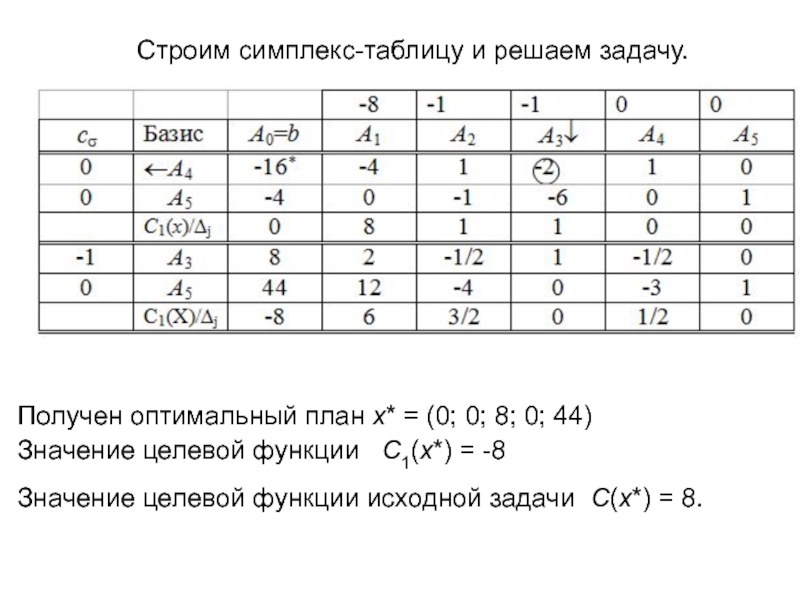
- 14. Строим симплекс-таблицу и решаем задачу.Получен оптимальный план
- 15. Признак отсутствия допустимых планов Теорема. Признак неразрешимости
- 16. П р и м е р. Выполнив эквивалентные преобразования получаем:Составим симплексную таблицу:
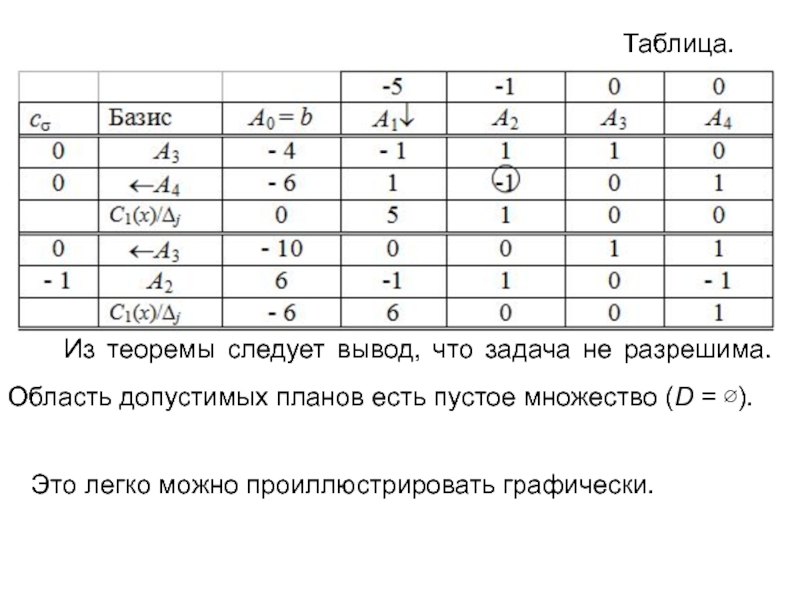
- 17. Таблица. Из теоремы следует вывод,
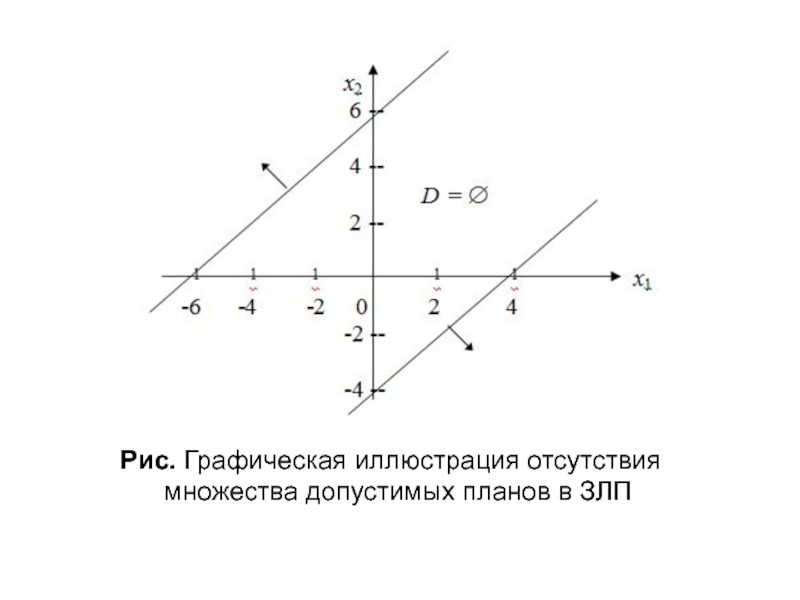
- 18. Рис. Графическая иллюстрация отсутствия множества допустимых планов в ЗЛП
- 19. Решение ЗЛП с дополнительным активным ограничением Допустим,
- 20. Добавим к исходной ЗЛП (1) дополнительное активное
- 21. Выразим xk из (7) и подставим в уравнение (10). Получим уравнение (11).(11)
- 22. Выделим и сгруппируем свободные переменные, а постоянные
- 23. Действительно, n новых
- 24. П р и м е р 19.
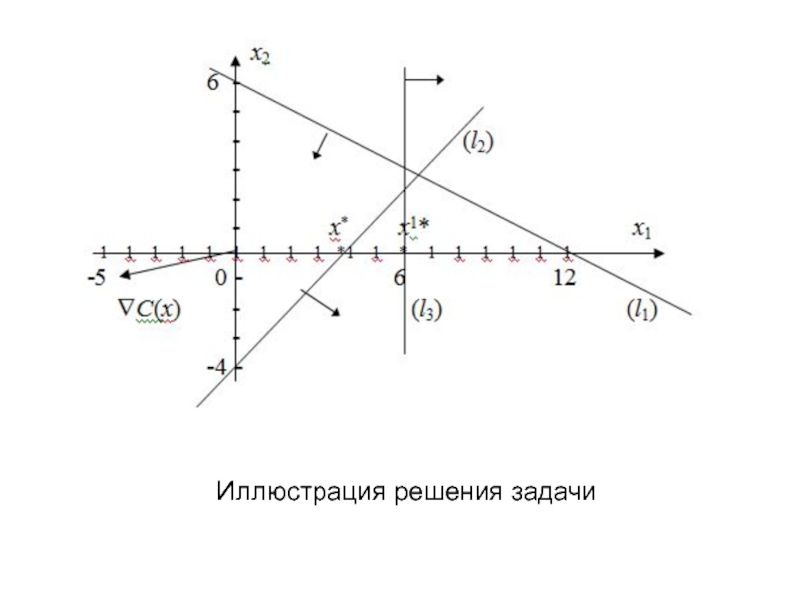
- 25. (l1) и (l2) обозначения прямых линий, ограничивающих соответствующие полуплоскости.
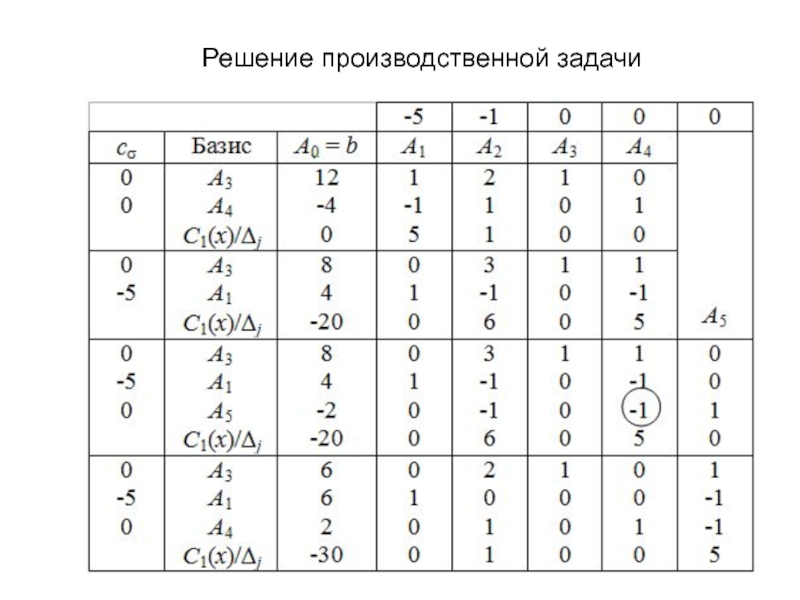
- 26. Решение производственной задачи
- 27. Получен оптимальный план х* = (4; 0;
- 28. Применяя алгоритм двойственного симплекс-метода, получаем оптимальный план
- 29. Иллюстрация решения задачи
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Двойственный симплекс-метод
Приведем к каноническому виду, введя дополнительные переменные х3,
х4, х5 0.
Слайд 3 Векторы А3, А4, А5 образуют единичный базис
этой ЗЛП. Частным решением будет вектор х0 =
(0; 0; 21; -3; -2).Здесь
.
Слайд 4Чаще всего псевдоплан появляется в задачах, в которых:
Ограничения имеют вид
Ах b.
Коэффициенты целевой функции сj 0,
и при этом C(х) min.В ЗЛП вводится существенное или активное ограничение, т.е. такое ограничение, которое изменяет оптимальный план в первоначально заданном множестве допустимых планов.
Слайд 5Теорема. Признак оптимальности псевдоплана.
Пусть х* = (х*1 ,…, х*n)
– псевдоплан, в котором
, тогда х* – оптимальный план.
Доказательство.
Так как х* псевдоплан, то ему соответствует некоторый базис. Поскольку по условию теоремы , то х* – БДП.
Из определения псевдоплана следует, что
При этом попадаем в условия теоремы «Признак оптимальности БДП». Таким образом, х* – оптимальный план.
.
Слайд 6Алгоритм двойственного симплекс-метода
(1)
Мы имеем систему ограничений вида:
(2)
В (2) все
координаты x0k не определены по знаку. При этом в ЗЛП
(2) все оценки.
Слайд 7Правило 1. Определение номера вектора, выводимого из
базиса.
Из базиса выводится вектор Ar , у которого номер r определяется из соотношения:
Слайд 8Правило 2. Определение номера вектора, вводимого в
базис.
Номер вектора s, вводимого в базис, выбирается из отношений двойственных оценок к отрицательным элементам r-ой строки симплекс-таблицы:Ведущим элементом будет
.
Слайд 9С помощью фрагмента симплекс-таблицы, запишем формулы пересчета ее элементов.
Таблица.
Фрагмент
симплекс-таблицы
Слайд 10 Компоненты нового псевдоплана определяются согласно (3).
(3)
Другие элементы симплексной таблицы вычисляются
по формулам:
(4)
Слайд 12Теорема 10.
Применение правил 1 и 2, а также формул (3)
(6) обеспечивает:
1) переход к новому псевдоплану, т. е.
гарантируетсяа)
б) новый псевдоплан хнов есть базисный план.
2) Значение целевой функции на новом псевдоплане не больше, чем значение целевой функции на предыдущем псевдоплане, т.е. С(хнов) С(х0).
Слайд 13П р и м е р 15.
Приведем ЗЛП к
каноническому виду
Базисный план х0 = (0; 0; 0; -16;
-4) есть псевдопланСлайд 14Строим симплекс-таблицу и решаем задачу.
Получен оптимальный план х* = (0;
0; 8; 0; 44)
Значение целевой функции C1(х*) =
-8 Значение целевой функции исходной задачи C(х*) = 8.
Слайд 15Признак отсутствия допустимых планов
Теорема. Признак неразрешимости ЗЛП в двойственном
симплекс-методе.
Пусть в ЗЛП (1) имеется псевдоплан х* = (x1*, …,
xr*, …, xn*) такой, что r-я координата меньше нуля, а все элементы r-й строки симплексной таблицы неотрицательны, тогда ЗЛП неразрешима. Слайд 17Таблица.
Из теоремы следует вывод, что задача не
разрешима. Область допустимых планов есть пустое множество (D = ).
Это легко можно проиллюстрировать графически.
Слайд 19Решение ЗЛП с дополнительным активным ограничением
Допустим, что ЗЛП (1)
имеет оптимальный план
Известен носитель оптимального плана
Последней итерации симплексной
таблицы соответствует система уравнений (7)
Координаты оптимального плана х*
Слайд 20Добавим к исходной ЗЛП (1) дополнительное активное или, как еще
говорят, существенное ограничение вида:
(8)
Введем в неравенство (8) дополнительную переменную
x
n+1 0. (9)
(10)
Слайд 22Выделим и сгруппируем свободные переменные, а постоянные члены перенесем в
правую часть уравнения (11):
(12)
Обозначим
переменная xn+1 = xm+1,0. Запишем (12)
в (m+1) строку симплекс-таблицы. Появляется новый единичный базисный вектор An+1., тогда дополнительная
За счет дополнительного ограничения (12) получили новую ЗЛП, в которой имеется псевдоплан
Слайд 23 Действительно, n новых двойственных оценок равны
прежним двойственным оценкам, а оценка n+1 = 0, как оценка
базисного вектора An+1. Кроме того, xm+1,0 0,так как
в силу предположения, что
дополнительное ограничение активное.
Имея псевдоплан, можно продолжать решение ЗЛП двойственным симплекс-методом.
Слайд 24П р и м е р 19.
Предприятие изготавливает для
постоянного заказчика изделие А основной номенклатуры и изделие В второстепенной
номенклатуры. Издержки на производство одного изделия А равны 5 ден. ед., а изделия В – 1 ден. ед.Заказчик требует как минимум на четыре единицы больше изделия А , чем изделия В. Производство одного изделия А дает единицу токсичных отходов, а изделия В – две единицы отходов. Общее количество токсичных отходов не должно превышать 12 единиц. Необходимо так организовать производство, чтобы минимизировать издержки.
Слайд 27Получен оптимальный план х* = (4; 0; 8; 0)
Издержки
составят С(х*) = 20 ден. ед.
Теперь обстоятельства изменились. Заказчик потребовал
изготовить не менее 6 штук изделий А. Появляется новое активное ограничение х1 6 (обозначим соответствующую прямую l3). Вводим дополнительную переменную х5 0
Слайд 28Применяя алгоритм двойственного симплекс-метода, получаем оптимальный план
х1* =
(6; 0; 6; 2; 0), С(х1*) = 30 ден.
ед. Геометрическая иллюстрация решения данной задачи показана на рис.Выразим х1 из второго уравнения и подставим
в третье уравнение. Тогда