Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ
Содержание
- 1. ЕГЭ
- 2. Слайд 2
- 3. КодификаторРешать простейшие стереометрические задачи на нахождение геометрических
- 4. Необходимая теорияТеорема ПифагораТеорема косинусовОпределение тригонометрических функций в
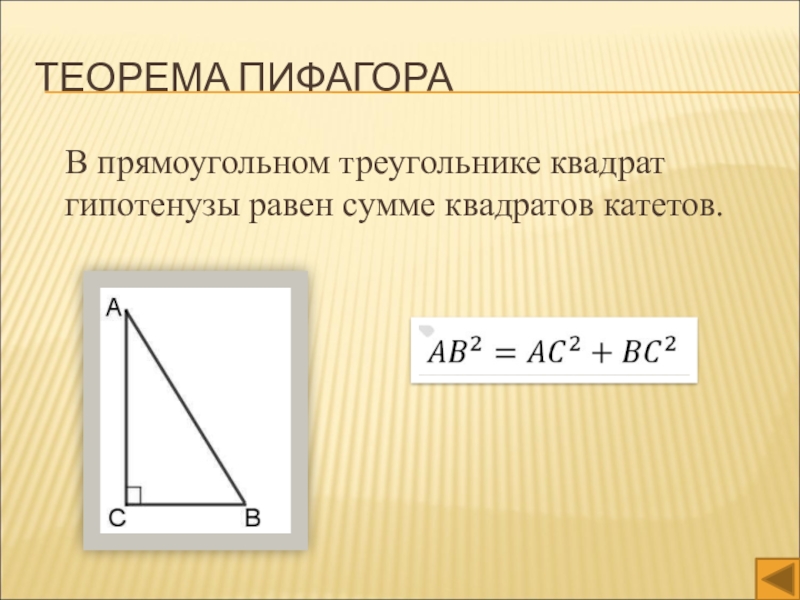
- 5. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 6. Теорема косинусов Квадрат любой стороны треугольника
- 7. Определение тригонометрических функций в прямоугольном треугольнике
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
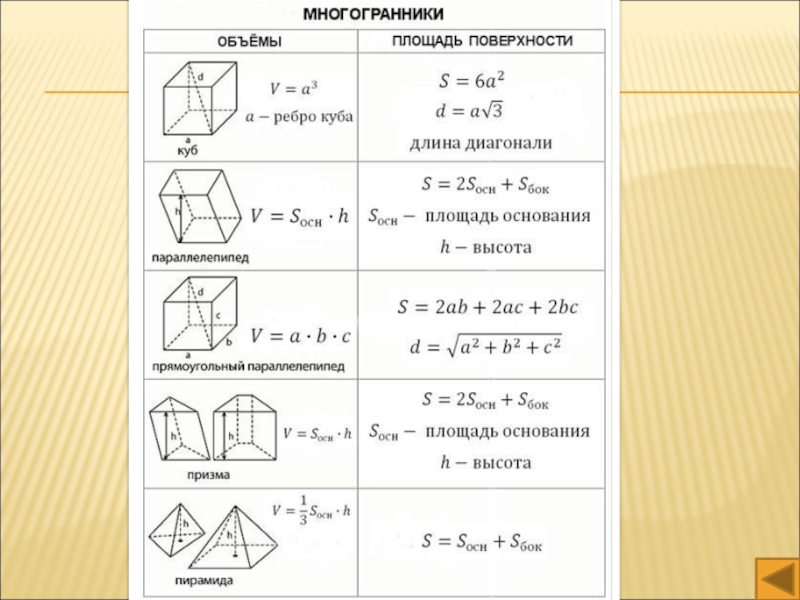
- 12. Прототипы заданий №8 Многогранники
- 13. Куб
- 14. Если каждое ребро куба увеличить на 1,
- 15. Прямоугольный параллелепипед
- 16. Слайд 16
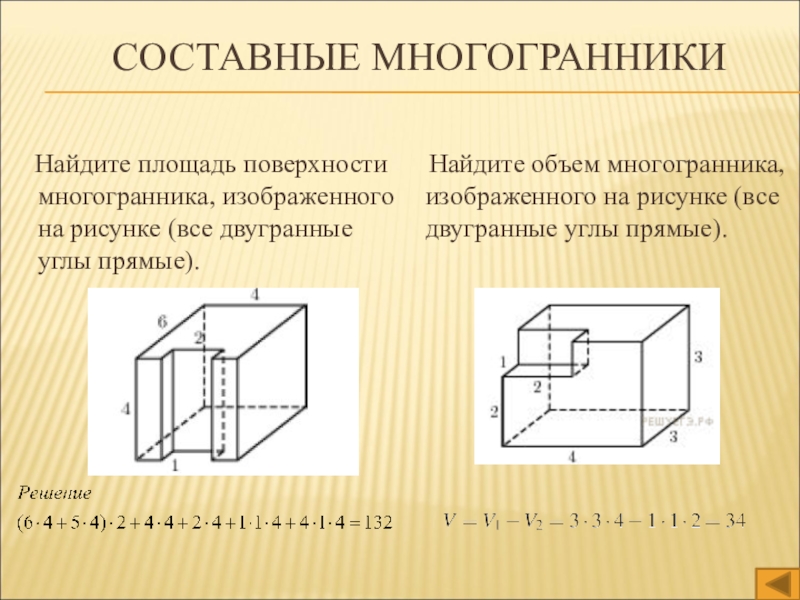
- 17. Составные многогранники Найдите площадь поверхности многогранника,
- 18. призма
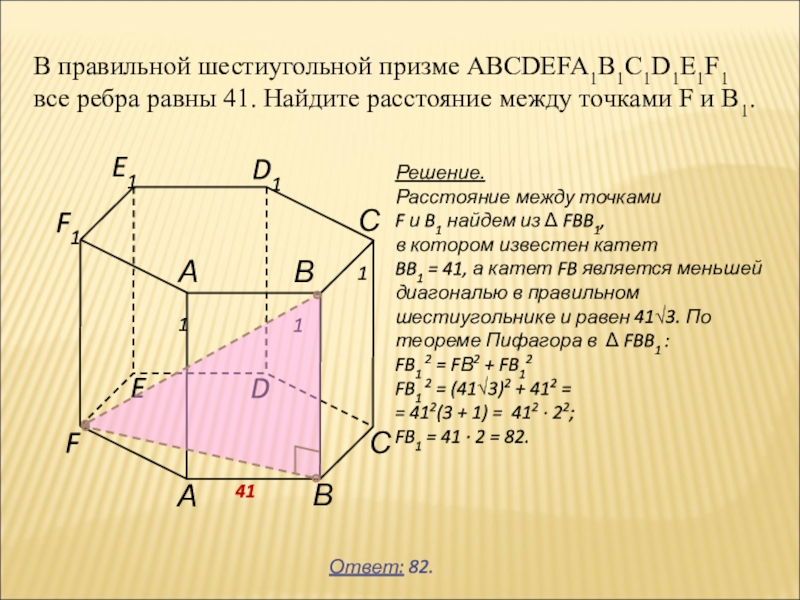
- 19. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра
- 20. Ответ: 60. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
- 21. пирамида
- 22. Ответ: 40. В правильной треугольной пирамиде боковое
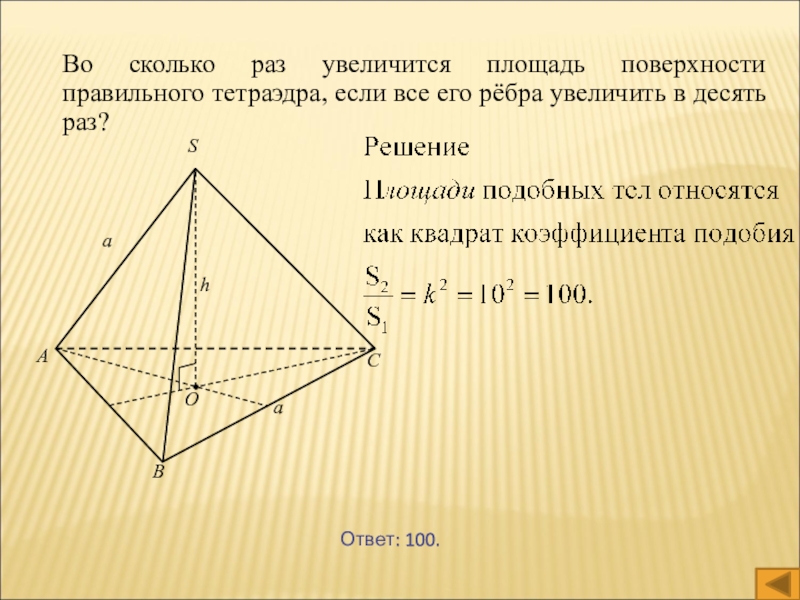
- 23. Во сколько раз увеличится площадь поверхности правильного
- 24. Ответ: 4200. Решение.Найдите площадь поверхности правильной четырехугольной
- 25. Решение.Основанием пирамиды служит прямоугольник, одна боковая грань
- 26. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое
- 27. От треугольной пирамиды, объём которой равен 120,
- 28. Объём параллелепипеда ABCDA1B1C1D1 равен 4500. Найдите объём треугольной пирамиды AD1CB1.Решение (см. анимацию)Ответ: 1500. DBCAB1C1A1D1
- 29. Одна цилиндрическая кружка вдвое выше второй, зато
- 30. Диаметр основания конуса равен 14,
- 31. ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы
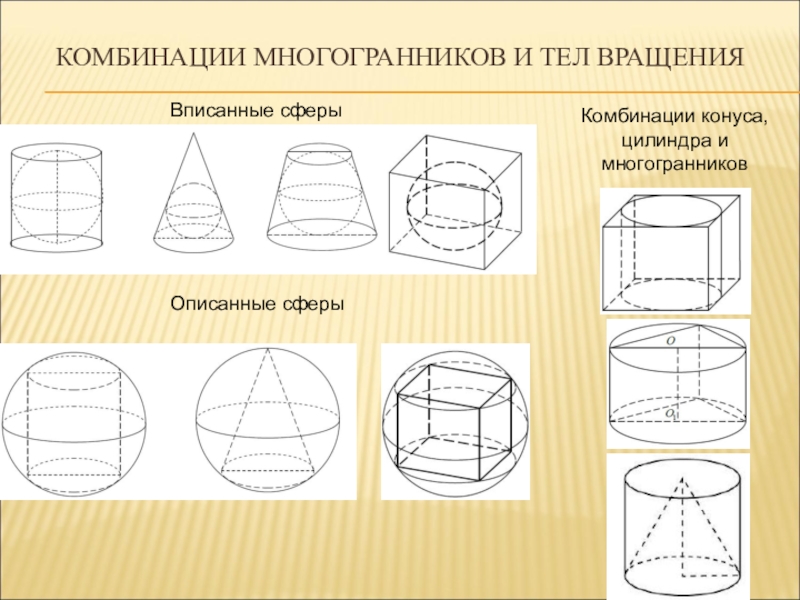
- 32. Комбинации многогранников и тел вращенияВписанные сферыОписанные сферыКомбинации конуса, цилиндра и многогранников
- 33. Шар вписан в цилиндр.
- 34. СПАСИБО ЗА ВНИМАНИЕ!
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Кодификатор
Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов,
площадей, объёмов);
Слайд 4Необходимая теория
Теорема Пифагора
Теорема косинусов
Определение тригонометрических функций в прямоугольном треугольнике
Формулы площадей
поверхностей и объемов тел
Отношение площадей подобных фигур
Отношение объемов подобных тел
Слайд 5Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов.
Слайд 6Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов
двух других сторон, без удвоенного произведения этих сторон на косинус
угла между ними.Слайд 7
Определение тригонометрических функций в прямоугольном треугольнике
Синус острого угла в прямоугольном
треугольнике — это отношение
противолежащего катета к гипотенузе:
Косинус острого угла в Тангенс острого угла в
прямоугольном треугольнике - в прямоугольном треугольнике -
отношение прилежащего катета отношение противолежащего
к гипотенузе: катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Слайд 12Прототипы заданий №8
Многогранники
Куб
Прямоугольный параллелепипед
Составные многогранники Призма
Пирамида
Тела вращения
Цилиндр
Конус
Сфера и шар
Комбинации тел
Слайд 14Если каждое ребро куба увеличить на 1, то площадь его
поверхности увеличится на 30. Найдите ребро куба.
Ответ: 2.
Решение.
S1=6a2,
S2=6(a+1)2S2= S1+30
6(a+1)2 = 6a2 +30
6a2 +2а+6- 6a2 - 30 = 0
2а=24
а=2
Слайд 16
Решение
Ответ: 32.
Два ребра прямоугольного параллелепипеда, выходящие из одной
вершины, равны 2, 4. Диагональ параллелепипеда равна 6.
Найдите объем параллелепипеда.
Слайд 17Составные многогранники
Найдите площадь поверхности многогранника, изображенного на рисунке
(все двугранные углы прямые).
Найдите объем многогранника, изображенного
на рисунке (все двугранные углы прямые).Слайд 19В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 41. Найдите
расстояние между точками F и B1.
Ответ: 82.
Решение.
Расстояние между
точками F и B1 найдем из FBB1,
в котором известен катет
BB1 = 41, а катет FB является меньшей диагональю в правильном шестиугольнике и равен 41√3. По теореме Пифагора в FBB1 :
FB1 2 = FВ2 + FB12
FB1 2 = (41√3)2 + 412 =
= 412(3 + 1) = 412 ∙ 22;
FB1 = 41 ∙ 2 = 82.
Слайд 20Ответ: 60.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны
20. Найдите угол СВЕ. Ответ дайте в градусах.
Решение.
Рассмотрим
СВЕ, в котором известен катет
ВС = 20, а катет ВЕ является большей диагональю в правильном шестиугольнике
и равен 40.
cosСВЕ = ВС : ВЕ = 20 : 40 = 0,5
СВЕ = 60
Слайд 22Ответ: 40.
В правильной треугольной пирамиде боковое ребро равно 50,
а сторона основания равна 30√3. Найдите высоту пирамиды.
Слайд 23Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все
его рёбра увеличить в десять раз?
Ответ: 100.
Слайд 24Ответ: 4200.
Решение.
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания
которой равны 60 и высота равна 40.
Слайд 25Решение.
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания,
а три другие боковые грани наклонены к плоскости основания под
углом 60°. Высота пирамиды равна 9. Найдите объём пирамиды.Ответ: 162.
Слайд 26Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно
30. Найдите объём пирамиды.
Ответ: 4500.
Решение.
Слайд 27От треугольной пирамиды, объём которой равен 120, отсечена треугольная пирамида
плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите
объём отсечённой треугольной пирамиды.Ответ: 30.
Решение.
Слайд 28Объём параллелепипеда ABCDA1B1C1D1 равен 4500. Найдите объём треугольной пирамиды AD1CB1.
Решение
(см. анимацию)
Ответ: 1500.
D
B
C
A
B1
C1
A1
D1
Слайд 29Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора
раза шире. Найдите отношение объема второй кружки к объему первой.
Решение
Обозначим
площадь и высоту второй кружки за S2 и V2. Тогда объем первой кружки
Ответ 1,125
Слайд 30 Диаметр основания конуса равен 14, а длина
образующей - 25. Найдите площадь осевого сечения
этого
конуса. Решение: Осевым сечением конуса является равнобедренный треугольник,
основание которого - диаметр D основания конуса, а высота h совпадает с высотой конуса.
По условию образующая конуса l = 25, радиус основания r = D / 2 = 14 / 2 = 7. Тогда:
Слайд 31ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы отсутствовали. Однако, выход
был найден: арбуз радиусом 3 дм приравнивали по стоимости к
трём арбузам радиусом 1 дм. Что вы возьмете? Правы ли были продавцы? R=3 дм R=1 дм
>
в 9 раз
Слайд 32Комбинации многогранников и тел вращения
Вписанные сферы
Описанные сферы
Комбинации конуса,
цилиндра и
многогранников
Слайд 33 Шар вписан в цилиндр. Площадь полной поверхности
цилиндра равна 18. Найдите площадь поверхности шара
Решение.
Площадь поверхности шара радиуса r равна
, то есть в 1,5 раза меньше площади поверхности цилиндра.
Следовательно, площадь поверхности шара равна 12.
Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна
Ответ: 12.