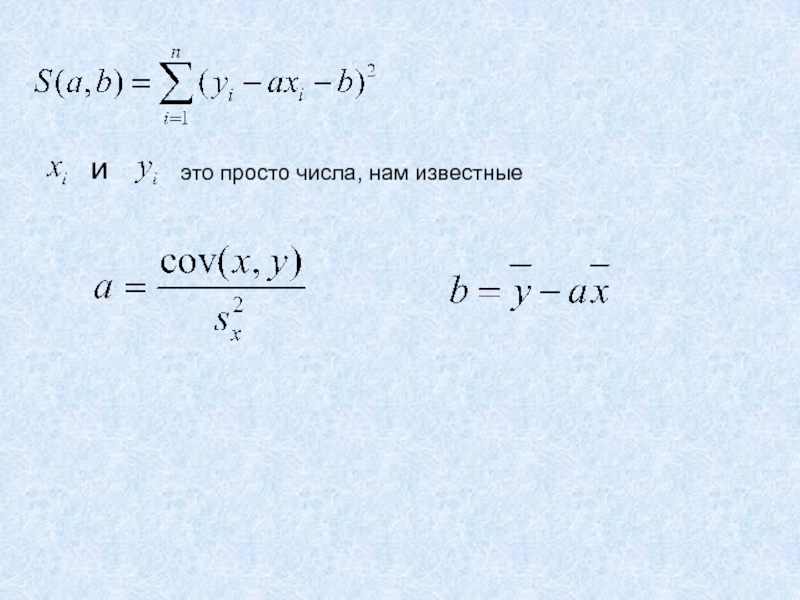Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:
Содержание
- 1. ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:
- 2. ЧТО ТАКОЕ ЭКОНОМЕТРИКАЭкономическая теорияТеория Вероятностей и математическая статистикаЭкономическая статистикаМикроэкономикаМакроэкономикаЭконометрика
- 3. Эконометрика Формулирует экономические модели, основываясь на экономической
- 4. ПОСЛЕДОВАТЕЛЬНОСТЬ ЭТАПОВ ЭКОНОМЕТРИЧЕСКОГО ИССЛЕДОВАНИЯЭкономическая теорияЭконометрическая модельОценка
- 5. Пример: Экономическая теория:1) C=f(P,Y) – потребление некоторого
- 6. Пределы данной моделиЭкономическая теория сделала две вещи:Установила
- 7. 1) Выбор функциональной формыСуществует множество форм, которые удовлетворяют гипотезе, выдвинутой экономической теорией, например
- 8. 2) Оценка параметров функциональной формыДля оценки неизвестных
- 9. Дополнительные вопросы:Нет ли переменных, которые следовало бы
- 10. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая) переменнаях – независимая (объясняющая) переменная
- 11. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 12. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 13. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 14. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 15. Свойства коэффициента корреляции1)2) Если
- 16. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 17. ПАРНАЯ РЕГРЕССИЯКоэффициент корреляции близок к 1
- 18. Коэффициент корреляции близок к -1
- 19. Коэффициент корреляции близок к 0
- 20. 6. Если коэффициент корреляции не близок к 0 строим модель парной линейной регрессии
- 21. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 22. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИПредположим, что необходимо получить
- 23. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
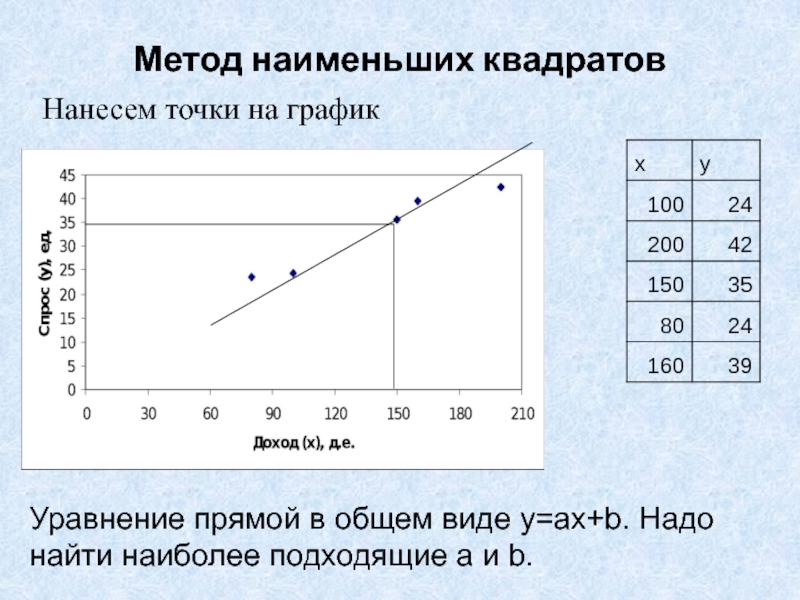
- 24. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИНанесем точки на график
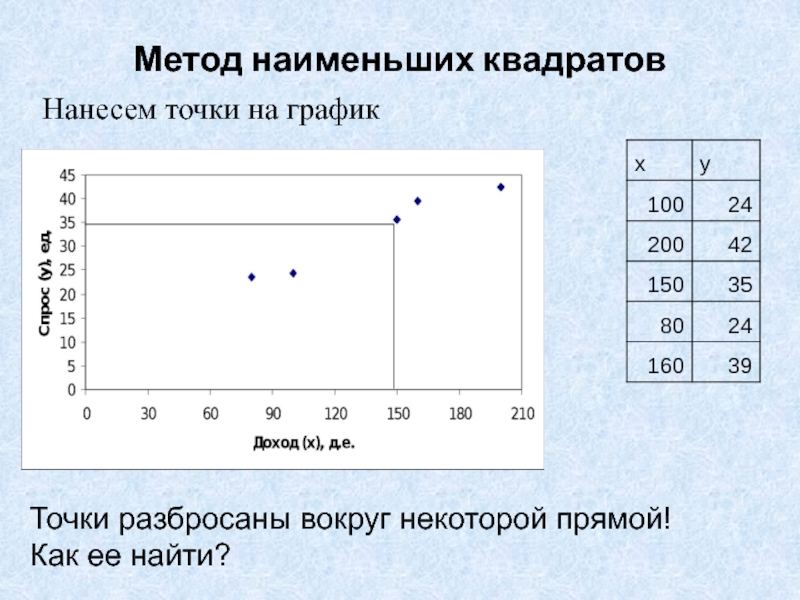
- 25. Метод наименьших квадратовНанесем точки на графикТочки разбросаны вокруг некоторой прямой!Как ее найти?
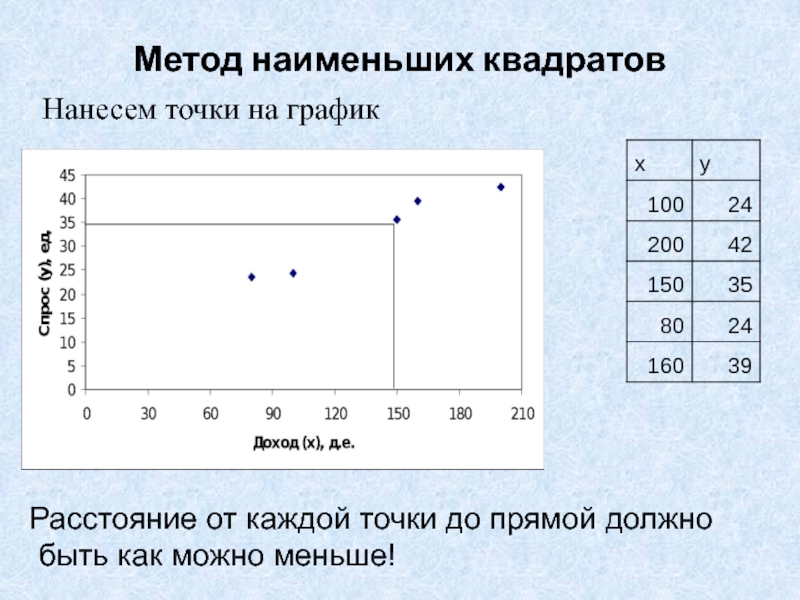
- 26. Метод наименьших квадратовНанесем точки на графикРасстояние от каждой точки до прямой должно быть как можно меньше!
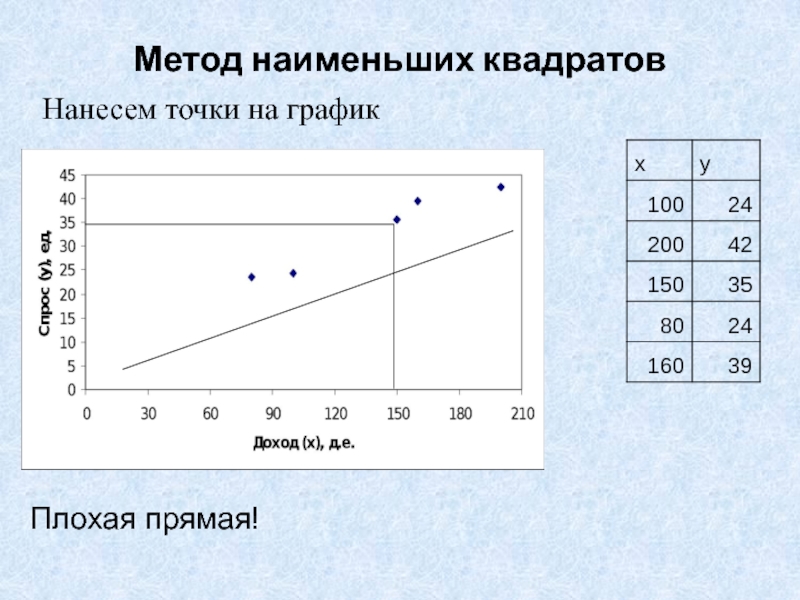
- 27. Метод наименьших квадратовНанесем точки на графикПлохая прямая!
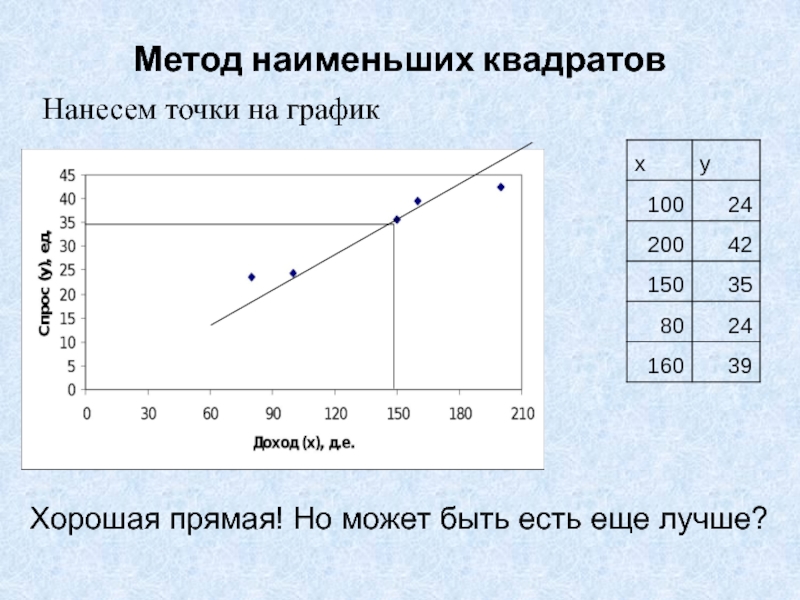
- 28. Метод наименьших квадратовНанесем точки на графикХорошая прямая! Но может быть есть еще лучше?
- 29. Метод наименьших квадратовНанесем точки на графикУравнение прямой
- 30. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+b
- 31. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
- 32. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
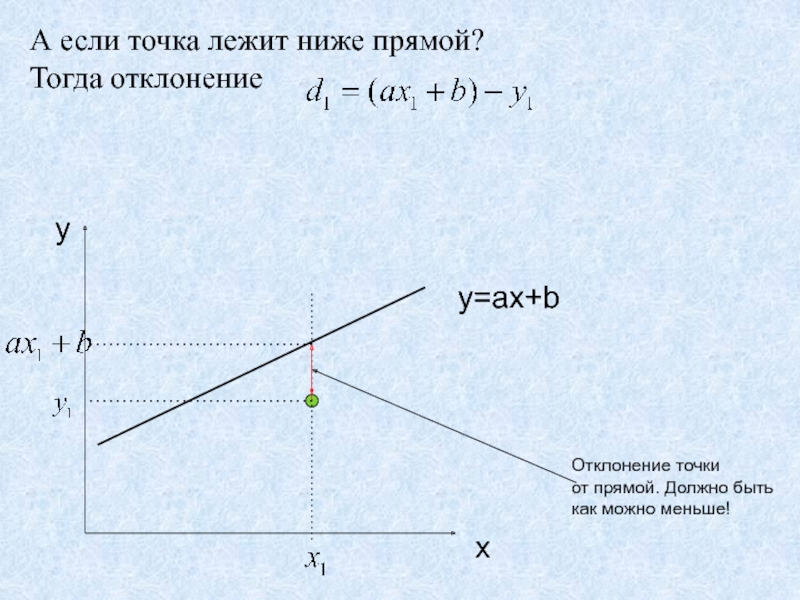
- 33. А если точка лежит ниже прямой?Тогда отклонение xyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
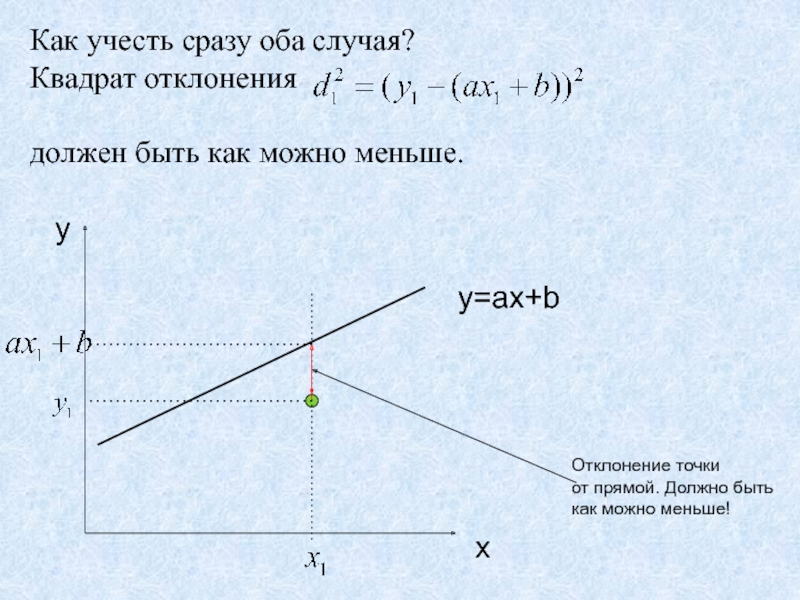
- 34. Как учесть сразу оба случая?Квадрат отклонения
- 35. Квадрат отклонения до второй точки тоже должен быть как можно меньше.
- 36. Квадрат отклонения до второй точки тоже должен быть как можно меньше.И для третьей точки
- 37. Предположим, что у нас n точек.Тогда и для последней точки
- 38. Как учесть все точки сразу?Сумма квадратов расстояний от точек до прямой должна быть как можно меньше.
- 39. Как учесть все точки сразу?Сумма квадратов расстояний от точек до прямой должна быть как можно меньше.обозначение
- 40. Как учесть все точки сразу?Получили функцию двух
- 41. это просто числа, нам известныеи
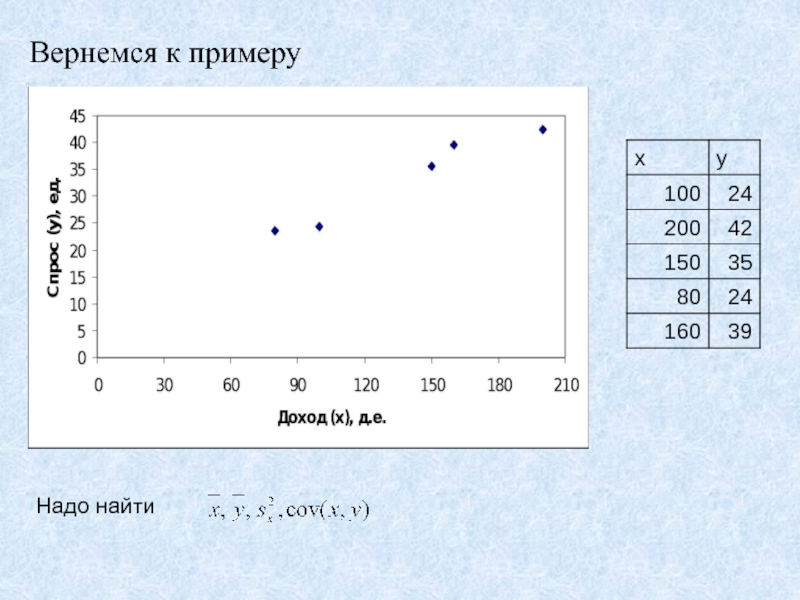
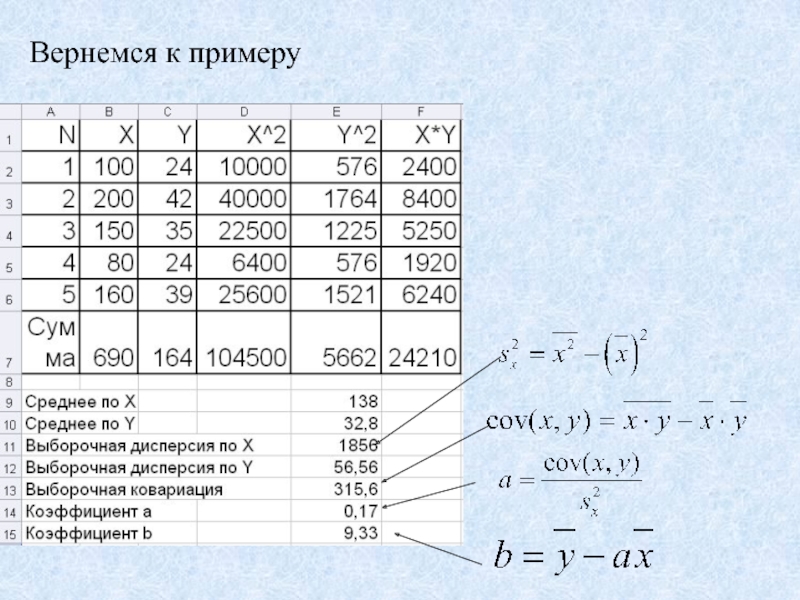
- 42. Вернемся к примеруНадо найти
- 43. Вернемся к примеру
- 44. a=0,17, b=9,33y=0,17x+9,33 - уравнение прямой, которая проходит ближе всего к точкам.
- 45. y=0,17x+9,33 - функция спроса в зависимости от
- 46. y=0,17x+9,33 - функция спроса в зависимости от
- 47. Интерпретация параметров уравнения регрессии y=ax+ba показывает на
- 48. y=0,17x+9,33 - функция спроса в зависимости от
- 49. Пример построения уравнения регрессииПри анализе зависимости
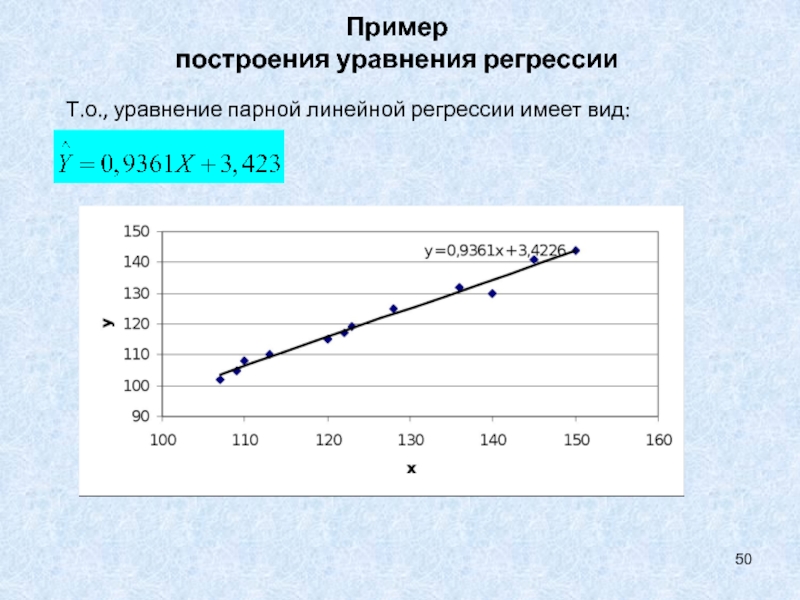
- 50. Пример построения уравнения регрессииТ.о., уравнение парной линейной регрессии имеет вид:
- 51. Пример построения уравнения регрессии
- 52. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИДанные 2002 г. о
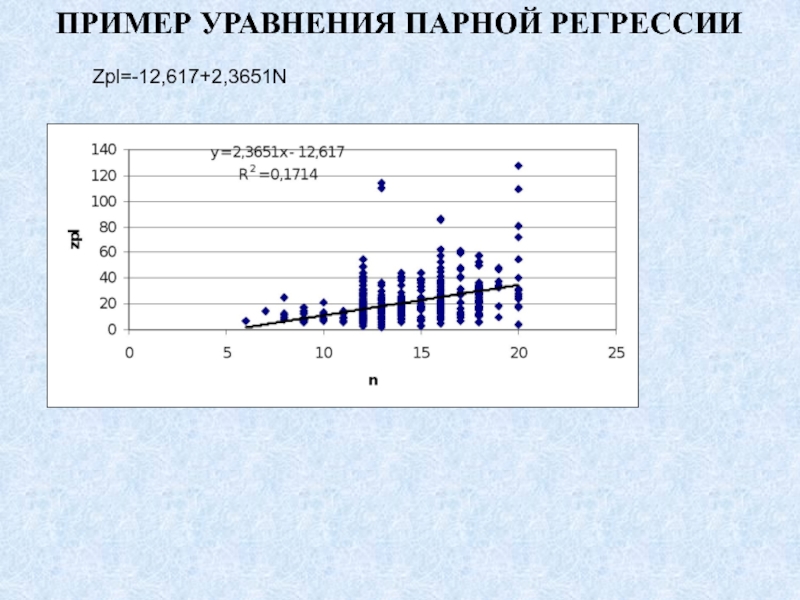
- 53. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl=-12,617+2,3651N
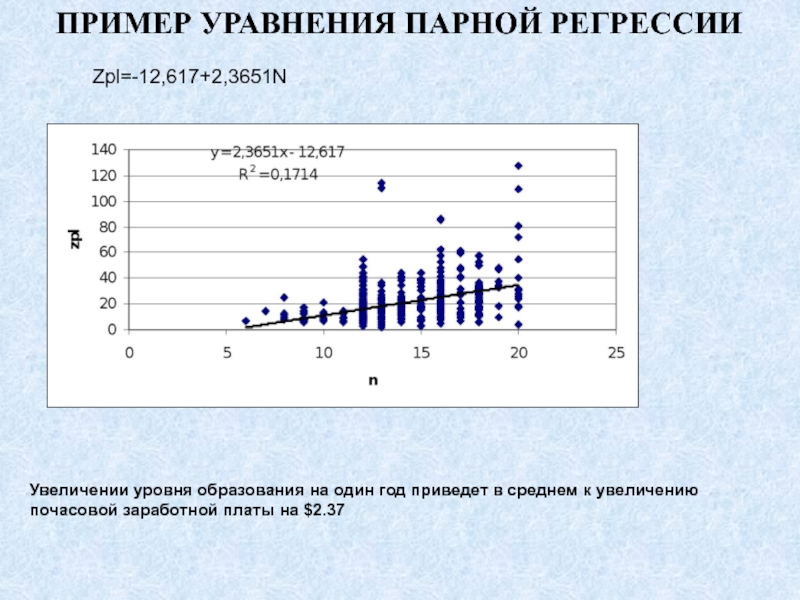
- 54. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl=-12,617+2,3651NУвеличении уровня образования на
- 55. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl= -12,6188+2,3651NДолжен ли индивид
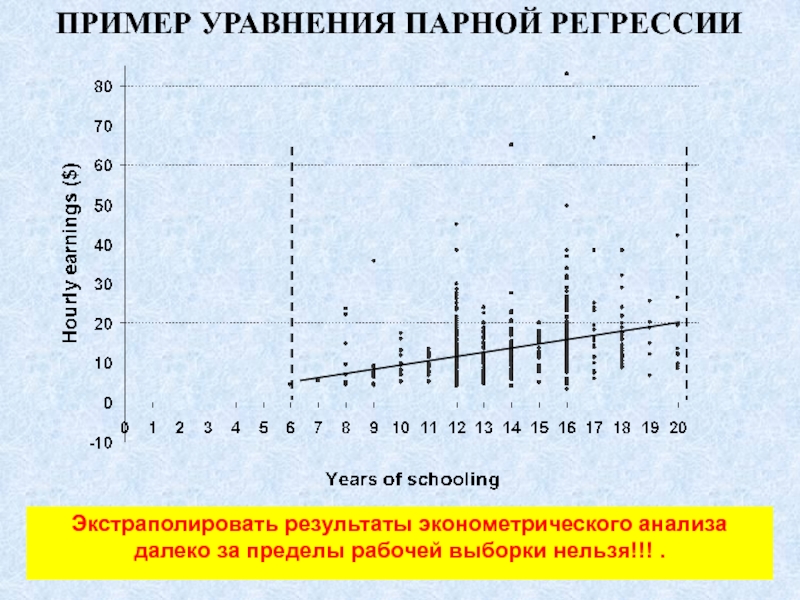
- 56. Экстраполировать результаты эконометрического анализа далеко за пределы рабочей выборки нельзя!!! . ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
- 57. Скорее всего зависимость почасовой заработной платы от количества лет обучения описывается нелинейным закономПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
- 58. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl=-12,6168+2,3651N
- 59. Скачать презентанцию
ЧТО ТАКОЕ ЭКОНОМЕТРИКАЭкономическая теорияТеория Вероятностей и математическая статистикаЭкономическая статистикаМикроэкономикаМакроэкономикаЭконометрика
Слайды и текст этой презентации
Слайд 1ЭКОНОМЕТРИКА
ЛИТЕРАТУРА К КУРСУ:
Основная
К.Доугерти
«Введение в эконометрику» , М.: Инфра-М
(пер. под
ред. Замкова)
Слайд 2ЧТО ТАКОЕ
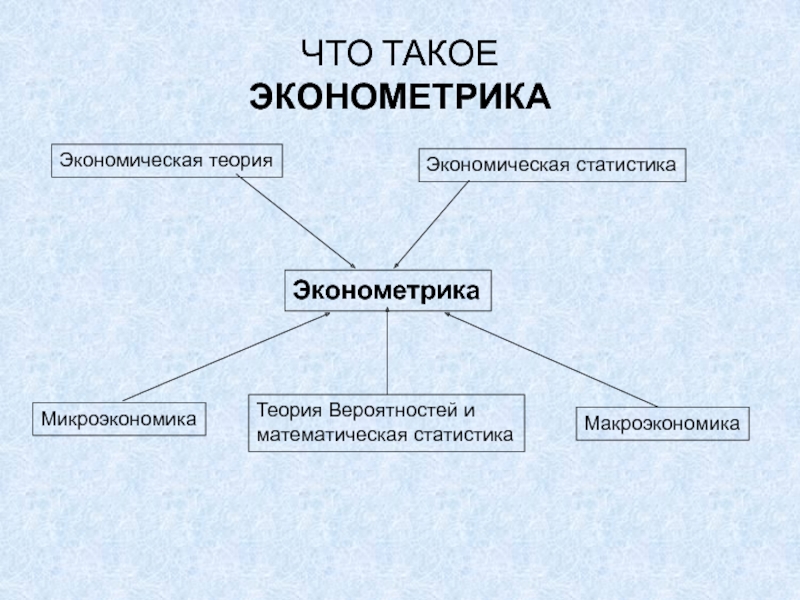
ЭКОНОМЕТРИКА
Экономическая теория
Теория Вероятностей и
математическая статистика
Экономическая статистика
Микроэкономика
Макроэкономика
Эконометрика
Слайд 3 Эконометрика
Формулирует экономические модели, основываясь на экономической теории (микро и
макроэкономике)
Оценивает неизвестные параметры модели на базе реальных статистических данных с
помощью методов математической статистикиИспользует построенные модели для прогнозирования и объяснения поведения исследуемых экономических показателей
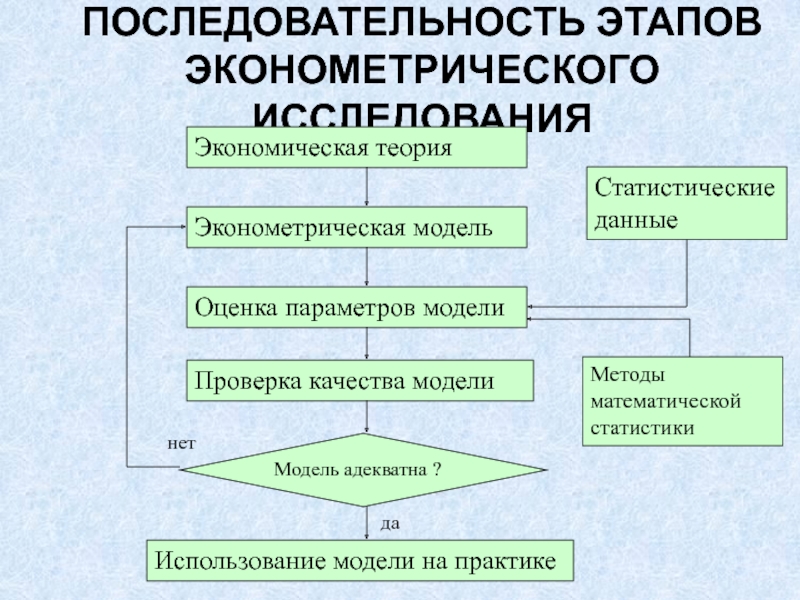
Слайд 4ПОСЛЕДОВАТЕЛЬНОСТЬ ЭТАПОВ
ЭКОНОМЕТРИЧЕСКОГО ИССЛЕДОВАНИЯ
Экономическая теория
Эконометрическая модель
Оценка параметров модели
Использование модели на
практике
Проверка качества модели
Статистические данные
Модель адекватна ?
нет
да
Методы математической статистики
Слайд 5Пример:
Экономическая теория:
1) C=f(P,Y) – потребление некоторого продукта в зависимости
от цены и дохода
предельное потребление по доходу положительно
предельное потребление по
цене отрицательно
Слайд 6Пределы данной модели
Экономическая теория сделала две вещи:
Установила перечень независимых переменных
в правой части уравнения.
Указала ожидаемые знаки в частных производных.
Слайд 71) Выбор функциональной формы
Существует множество форм,
которые удовлетворяют гипотезе, выдвинутой
экономической теорией, например
Слайд 82) Оценка параметров функциональной формы
Для оценки неизвестных параметров
т.е. наблюдения за потреблением, ценой и доходом за ряд лет.
Слайд 9Дополнительные вопросы:
Нет ли переменных, которые следовало бы дополнительно включить в
уравнение
Не следует ли исключить из уравнения некоторые переменные
Правильно ли выбрана
функциональная форма?Насколько точны полученные оценки параметров?
Слайд 10МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
Слайд 11МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
1. Вычисляем средние значения
СРЗНАЧ(диапазон
данных)
Слайд 12МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
2. Вычисляем дисперсии
ДИСПР(диапазон данных)
Слайд 13МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
3. Вычисляем ковариацию
КОВАР(диапазон данных х,
диапазон данных y)
Слайд 14МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
4. Вычисляем корреляцию
КОРРЕЛ(диапазон данных х,
диапазон данных y)
Слайд 15Свойства коэффициента корреляции
1)
2) Если
для всех i=1,…n, то
при a>0
при a<0
Коэффициент корреляции – мера линейной зависимости двух случайных
величин
Слайд 16МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
4. Анализируем коэффициент корреляции
Коэффициент корреляции
принимает значения от -1 до 1.Значения близкие к 1 – есть тесная прямая связь между х и у
Значения близкие к -1 – есть тесная обратная связь между х и у
Значения близкие к 0 – связь между х и у отсутствует
Слайд 21МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
a b – неизвестные параметры модели
- случайная составляющая
Слайд 22МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
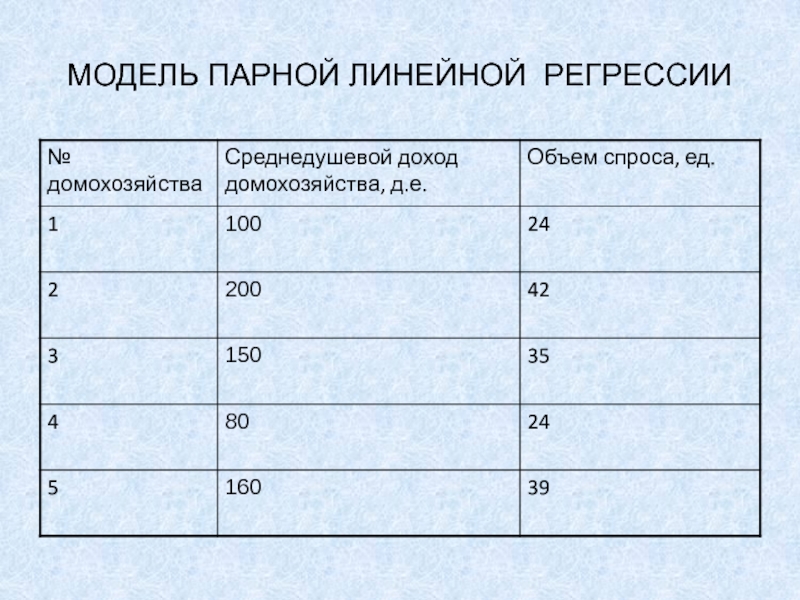
Предположим, что необходимо получить функцию
спроса на
некоторый товар в зависимости от дохода.
Проводится опрос домохозяйств.
1. Среднедушевой доход
домохозяйства?2. Сколько единиц товара приобрело домохозяйство за месяц?
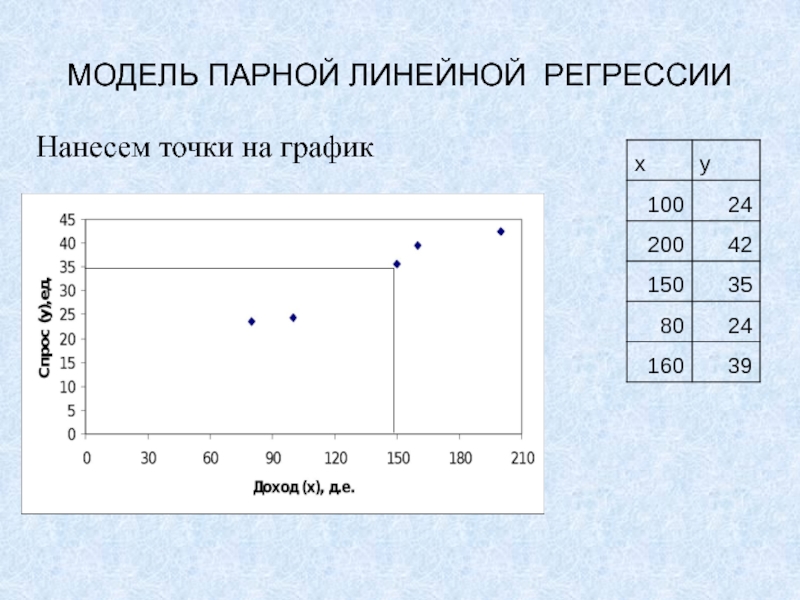
Слайд 25Метод наименьших квадратов
Нанесем точки на график
Точки разбросаны вокруг некоторой прямой!
Как
ее найти?
Слайд 26Метод наименьших квадратов
Нанесем точки на график
Расстояние от каждой точки до
прямой должно
быть как можно меньше!
Слайд 28Метод наименьших квадратов
Нанесем точки на график
Хорошая прямая! Но может быть
есть еще лучше?
Слайд 29Метод наименьших квадратов
Нанесем точки на график
Уравнение прямой в общем виде
y=ax+b. Надо
найти наиболее подходящие a и b.
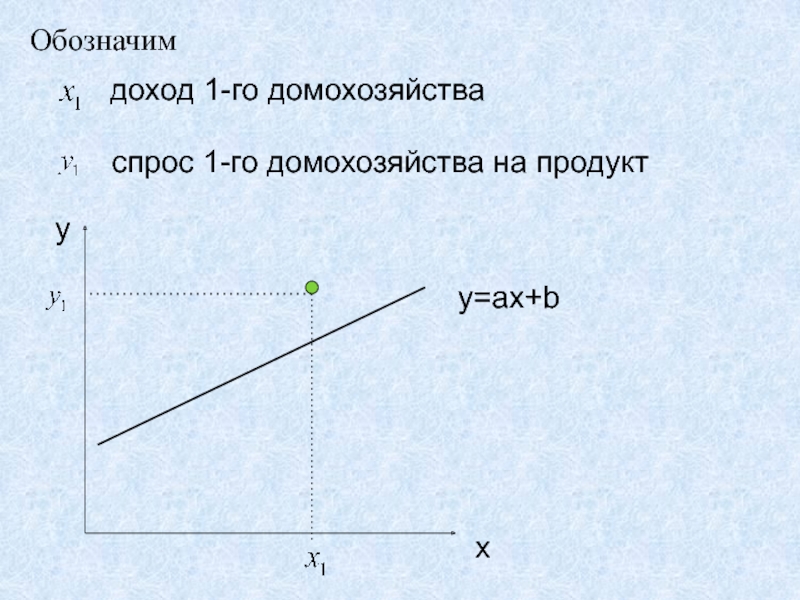
Слайд 31Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
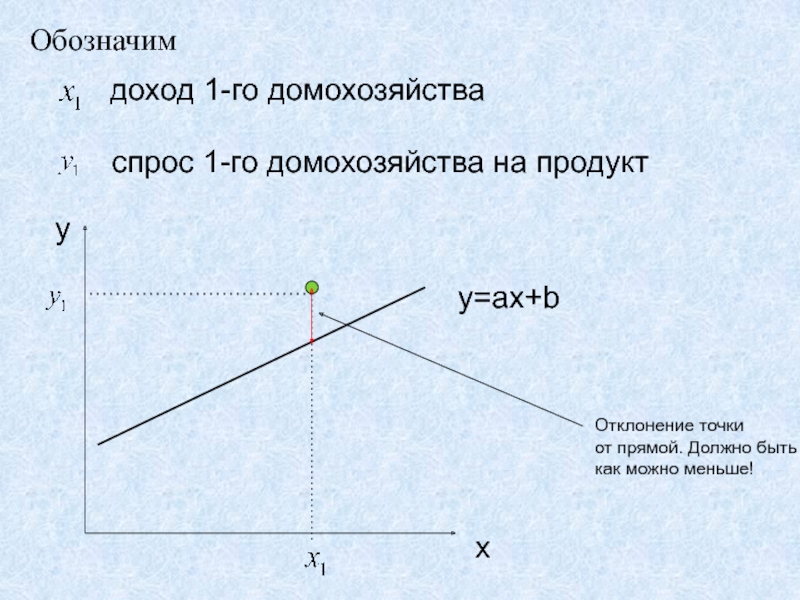
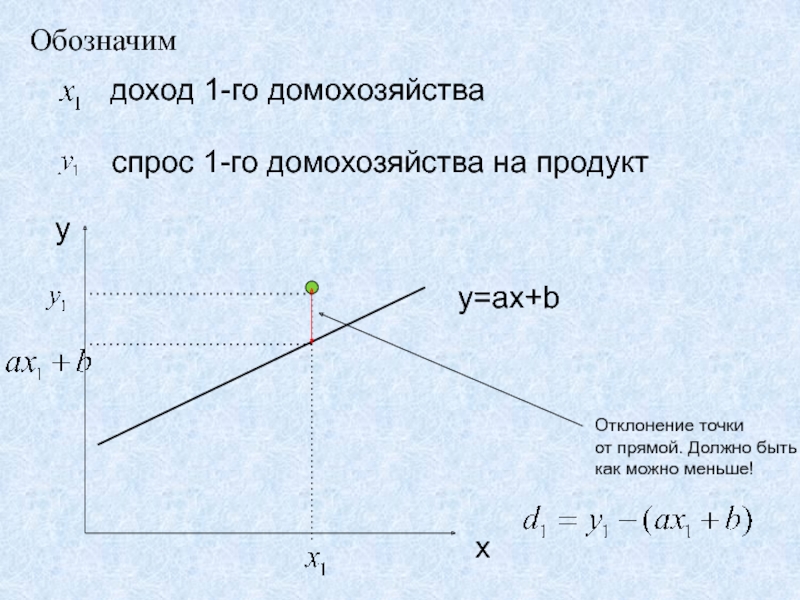
Слайд 32Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
Слайд 33А если точка лежит ниже прямой?
Тогда отклонение
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
Слайд 34Как учесть сразу оба случая?
Квадрат отклонения
должен быть как можно меньше.
x
y
y=ax+b
Отклонение точки
от прямой. Должно быть
как можно меньше!
Слайд 38Как учесть все точки сразу?
Сумма квадратов расстояний от точек до
прямой должна быть как можно меньше.
Слайд 39Как учесть все точки сразу?
Сумма квадратов расстояний от точек до
прямой должна быть как можно меньше.
обозначение
Слайд 40Как учесть все точки сразу?
Получили функцию двух переменных, для которой
надо найти минимум,
т.е. надо исследовать на экстремум.
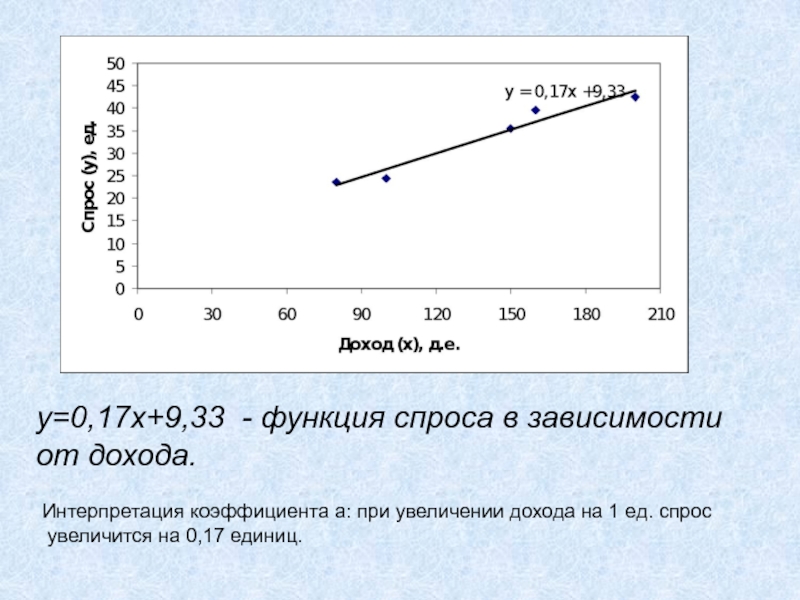
Слайд 45y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Интерпретация коэффициента а:
при увеличении дохода на 1 ед. спрос
увеличится на 0,17
единиц. 
Слайд 46y=0,17x+9,33 - функция спроса в зависимости
от дохода.
С ростом дохода
на 1 ден.ед. спрос на товар
растет на 0,17 ед.
Сервис
– Анализ данных
Слайд 47Интерпретация параметров уравнения
регрессии y=ax+b
a показывает на сколько единиц изменится
y,
если х увеличится на 1 единицу.
b показывает прогнозируемое значение
показателя y при показатели х=0 (если х=0
возможно).
Слайд 48y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Выполнить прогноз потребления
продукта
домохозяйством с доходом 200 д.е.
2)Найти предельную склонность к потреблению
продукта.
3)
Найти эластичность спроса по доходу при доходе 100 д.е. и 50 д.е.
Слайд 49Пример
построения уравнения регрессии
При анализе зависимости объема потребления Y (у.е.)
домохозяйства от располагаемого дохода X (у.е.) отобрана выборка объема n
= 12 (помесячно в течение года), результаты которой приведены в таблице:
Слайд 52
ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
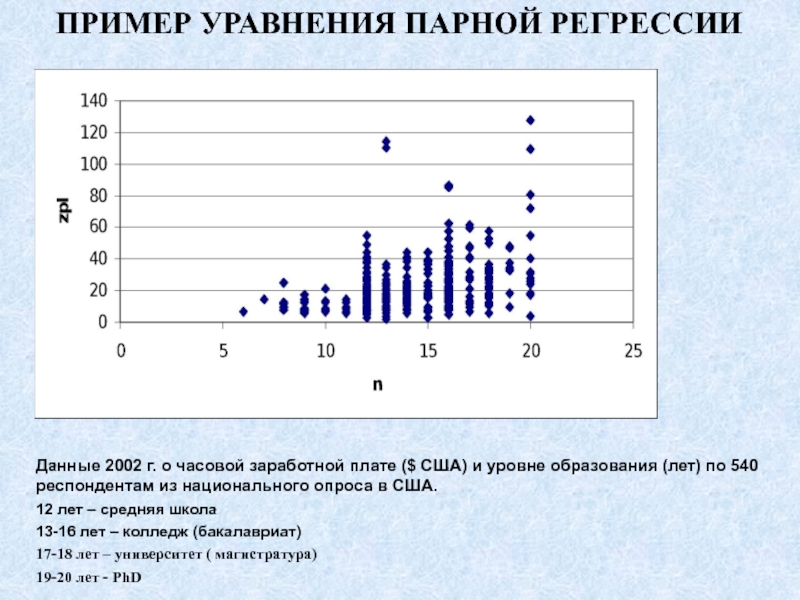
Данные 2002 г. о часовой заработной плате
($ США) и уровне образования (лет) по 540 респондентам из
национального опроса в США.12 лет – средняя школа
13-16 лет – колледж (бакалавриат)
17-18 лет – университет ( магистратура)
19-20 лет - PhD
Слайд 54ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl=-12,617+2,3651N
Увеличении уровня образования на один год приведет
в среднем к увеличению почасовой заработной платы на $2.37
Слайд 55ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl= -12,6188+2,3651N
Должен ли индивид платить за право
работы $12.62 в час, если он не имеет образования?.
Слайд 56Экстраполировать результаты эконометрического анализа далеко за пределы рабочей выборки нельзя!!!
.
ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Слайд 57Скорее всего зависимость почасовой заработной платы от количества лет обучения
описывается нелинейным законом
ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
