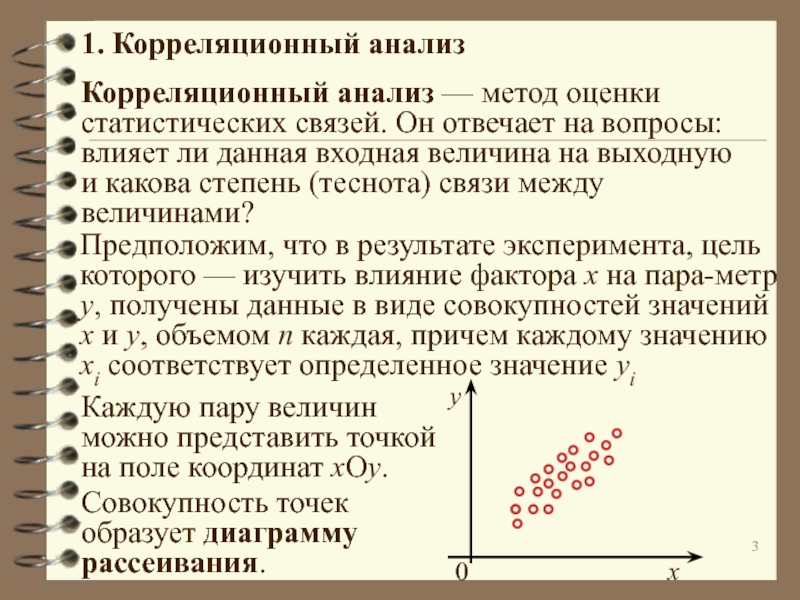
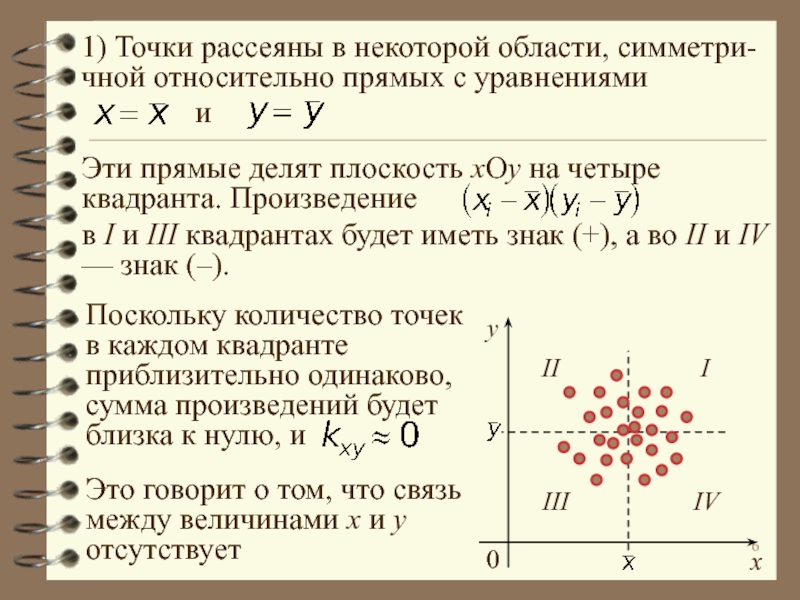
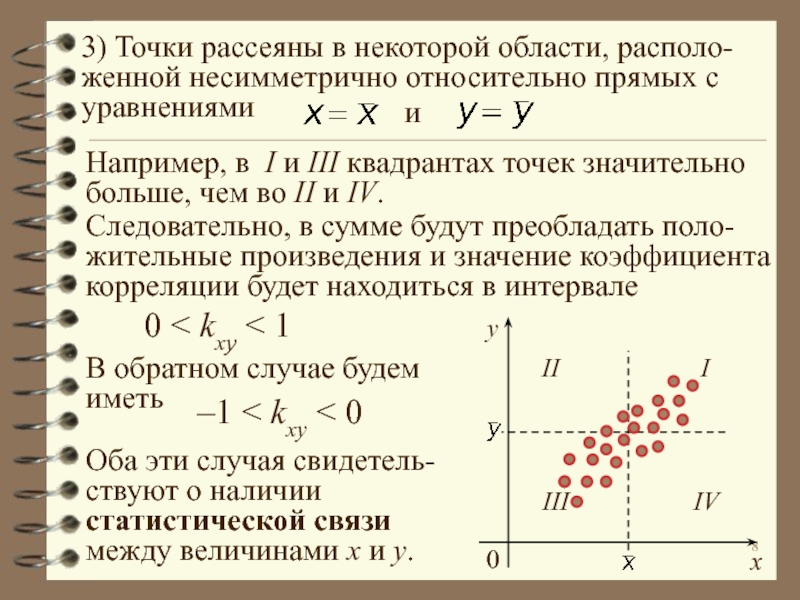
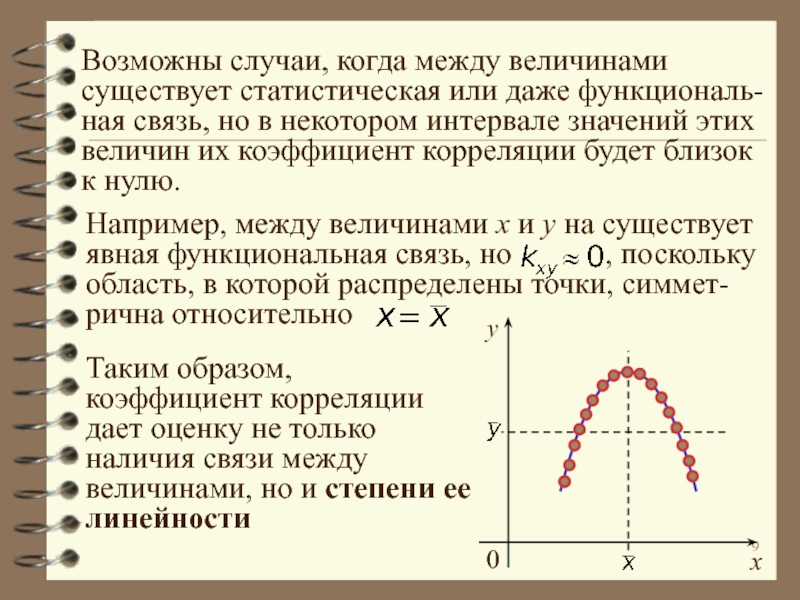
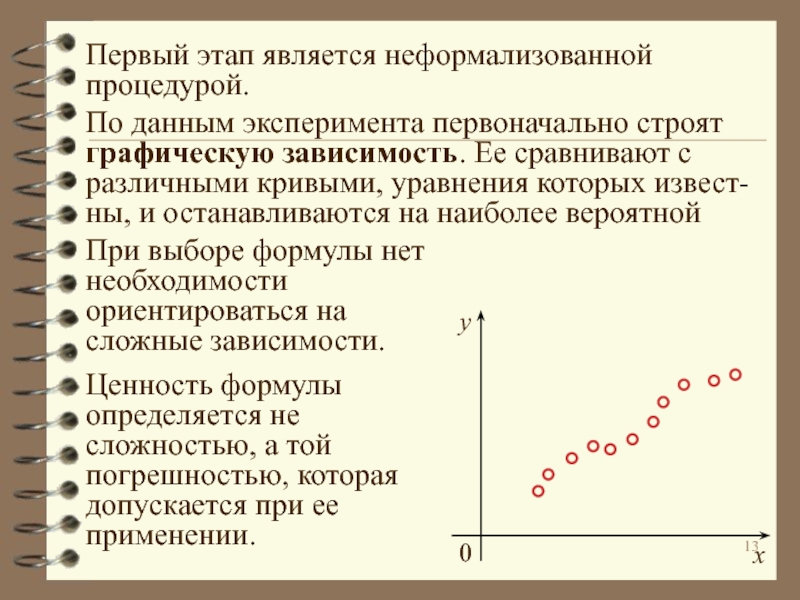
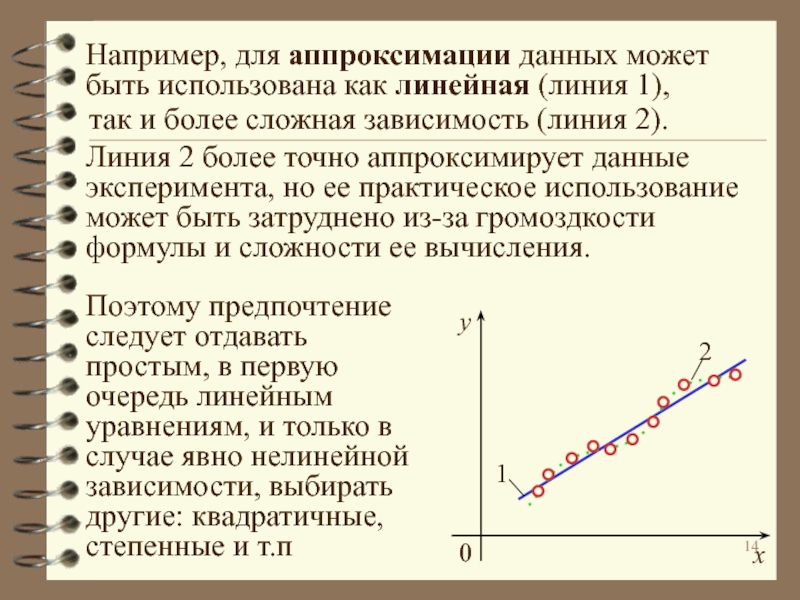
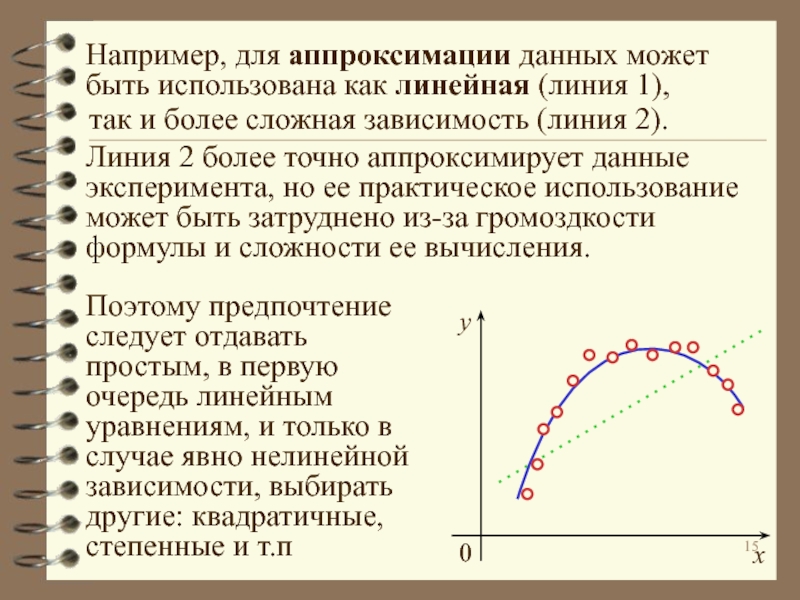
явлениями, параметрами и факторами.
Связи бывают функциональными и вероятностными (статистическими).
При функциональной связи каждому значению входной величины соответствует одно или нес-колько строго определенных значений выходной.
Статистические связи проявляются лишь при многократном испытании. При этом данному значению входной величины соответствует множество значений выходной.